13.1 轴对称同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
13.1 轴对称
一.选择题(共15小题)
1.若P是△ABC所在平面内的点,且PA=PB=PC,则下列说法正确的是( )
A.点P是△ABC三边垂直平分线的交点
B.点P是△ABC三条角平分线的交点
C.点P是△ABC三边上高的交点
D.点P是△ABC三边中线的交点
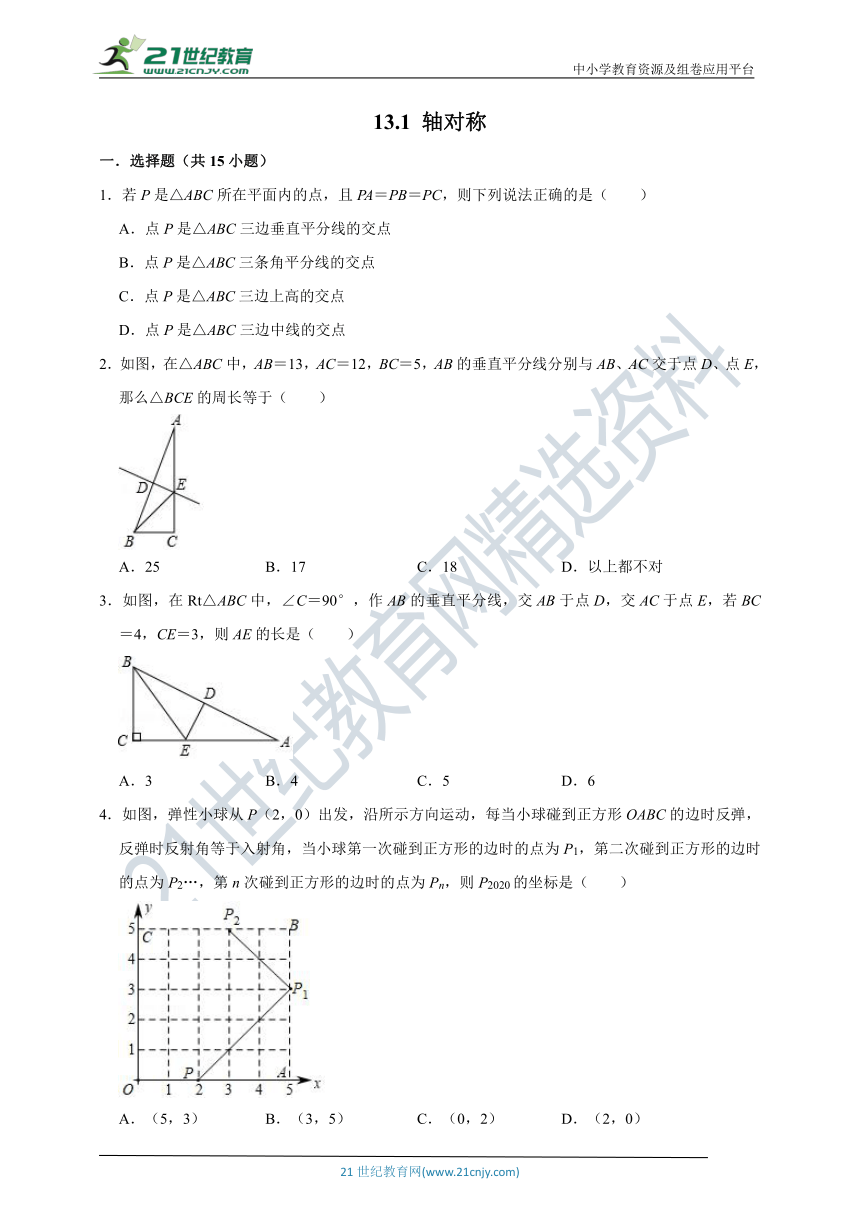
2.如图,在△ABC中,AB=13,AC=12,BC=5,AB的垂直平分线分别与AB、AC交于点D、点E,那么△BCE的周长等于( )
A.25 B.17 C.18 D.以上都不对
3.如图,在Rt△ABC中,∠C=90°,作AB的垂直平分线,交AB于点D,交AC于点E,若BC=4,CE=3,则AE的长是( )
A.3 B.4 C.5 D.6
4.如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
A.(5,3) B.(3,5) C.(0,2) D.(2,0)
5.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形DABC的边时反弹,反弹时反射角等于入射角,当小球第1次磁到正方形的边时的点为P1(﹣2,0),第2次碰到正方形的边时的点为P2,…,第n次碰到正方形的边时的点为Pn,则点P2019的坐标是( )
A.(0,1) B.(﹣4,1) C.(﹣2,0) D.(0,3)
6.如图是一个经过改造的规则为3×5的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋
7.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20° C.30° D.40°
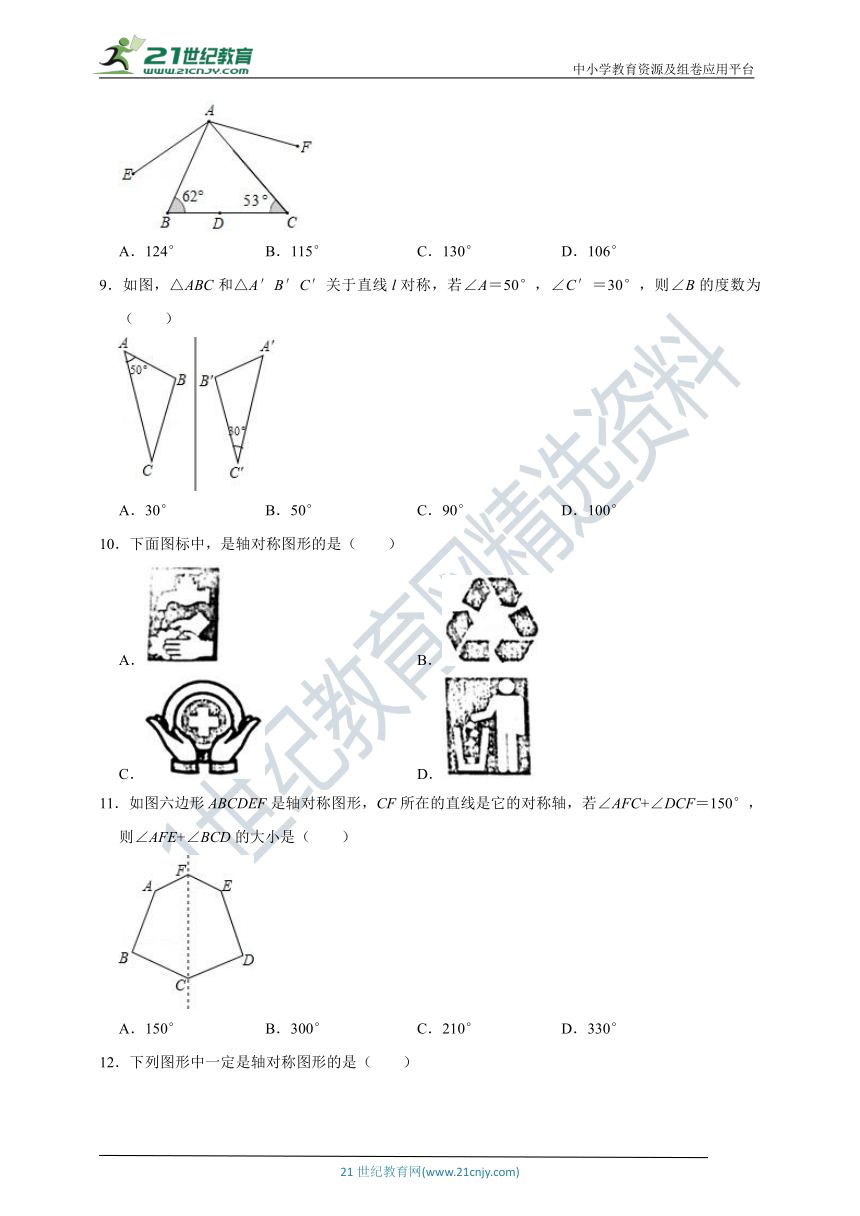
8.如图,△ABC中,D点在BC上,∠B=62°,∠C=53°,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.则∠EAF的度数为( )
A.124° B.115° C.130° D.106°
9.如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
A.30° B.50° C.90° D.100°
10.下面图标中,是轴对称图形的是( )
A. B.
C. D.
11.如图六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠DCF=150°,则∠AFE+∠BCD的大小是( )
A.150° B.300° C.210° D.330°
12.下列图形中一定是轴对称图形的是( )
A. B.
C. D.
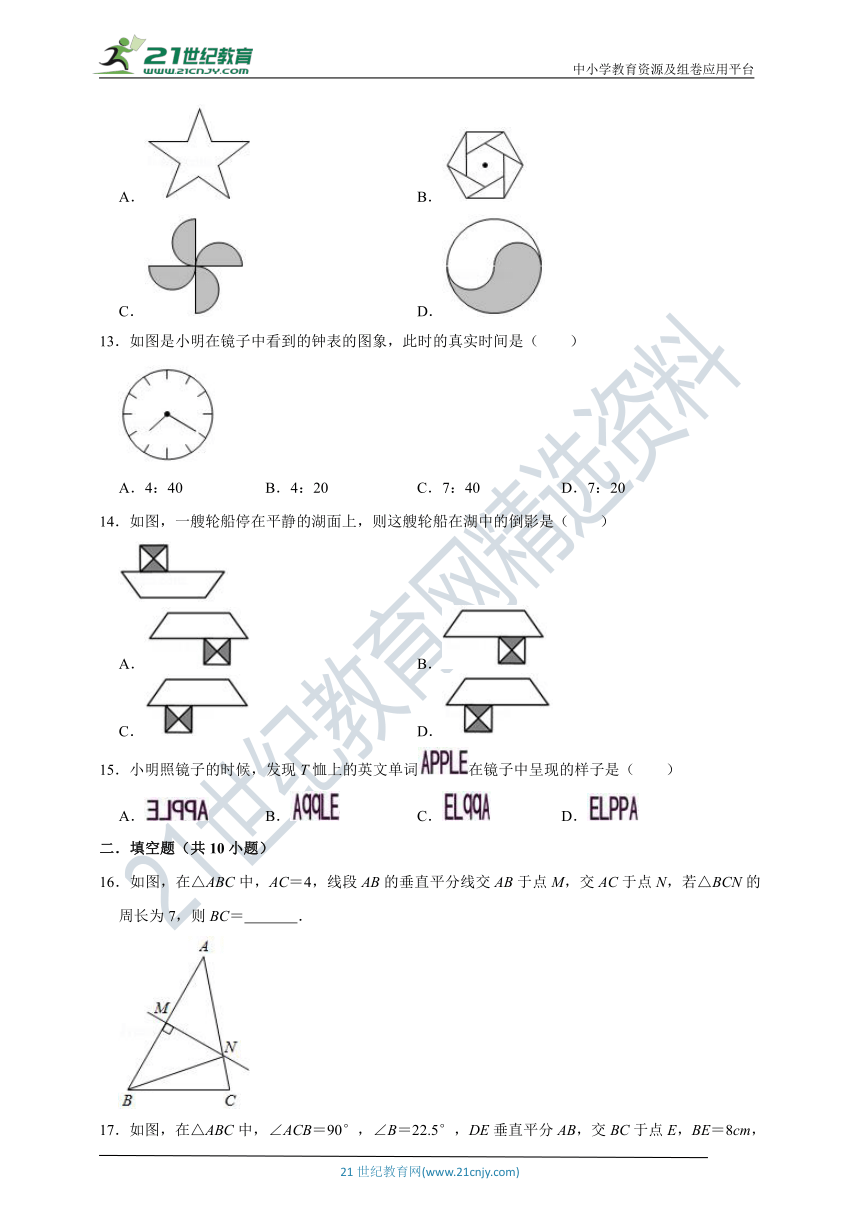
13.如图是小明在镜子中看到的钟表的图象,此时的真实时间是( )
A.4:40 B.4:20 C.7:40 D.7:20
14.如图,一艘轮船停在平静的湖面上,则这艘轮船在湖中的倒影是( )
A. B.
C. D.
15.小明照镜子的时候,发现T恤上的英文单词在镜子中呈现的样子是( )
A. B. C. D.
二.填空题(共10小题)
16.如图,在△ABC中,AC=4,线段AB的垂直平分线交AB于点M,交AC于点N,若△BCN的周长为7,则BC= .
17.如图,在△ABC中,∠ACB=90°,∠B=22.5°,DE垂直平分AB,交BC于点E,BE=8cm,则AC等于 cm.
18.如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入 号球袋.
19.在日常生活中,你会注意到有一些含有特殊数字规律的车牌号码,如:浙A80808,浙A22222,浙A12321等,这些牌照中的五个数字都是关于中间的一个数字“对称”的,给人以对称美的感受,我们不妨把这样的牌照叫做“数字对称”牌照.如果让你负责制作只以8或9开头且有5个数字的“数字对称”牌照,那么最多可制作 个.
20.如图,△ABC中,∠ACB=90°,BC=6,AC=8,AB=10,动点P在边AB上运动(不与端点重合),点P关于直线AC,BC对称的点分别为P1,P2.则在点P的运动过程中,线段P1P2的长的最小值是 .
21.如图,∠MON内有一点P,点P关于OM的轴对称点是G,点P关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=35°,则∠GOH= .
22.如图,3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有 个.
23.下列四个图案中,具有一个共有的性质,那么在222,606,808,609下面四个数中,满足上述性质的一个是 .
24.一个汽车牌照号码在水中的倒影为,则该车牌照号码为 .
25.在上学的路上,小刚从电瓶车的后视镜里看到一辆汽车,车顶字牌上的字在平面镜中的像是IXAT,则这辆车车顶字牌上的字实际是 .
三.解答题(共5小题)
26.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)直接写出∠BAC的度数;
(2)求∠DAF的度数,并注明推导依据;
(3)若△DAF的周长为20,求BC的长.
27.小惠同学学习了轴对称知识后,忽然想起了过去做过的一道题:有一组数排列成方阵,如图所示,试计算这组数的和,小惠想方阵就像小正方形,正方形是轴对称图形,能不能利用轴对称的思想来解决方阵的问题呢?小惠试了试,竟得到了非常巧妙的方法.请你试试看!
28.如图,点P关于OA、OB轴对称的对称点分别为C、D,连结CD,交OA于M,交OB于N.
(1)若CD的长为18厘米,求△PMN的周长;
(2)若∠CPD=131°,∠C=21°,∠D=28°,求∠MPN.
29.如图,在4×4的正方形网格中,有5个黑色小正方形.
(1)请你移动一个黑色小正方形,使移动后所形成的4×4的正方形网格图形是轴对称图形.如:将8号小正方形移至14号;你的另一种做法是将 号小正方形移至 号(填写标号即可);
(2)请你移动2个小正方形,使移动后所形成的图形是轴对称图形,你的一种做法是将 号小正方形移至 号、将 号小正方形移至 号(填写标号即可).
30.舞蹈教室的东西墙壁有平面镜AC、BD,如图小华在平面镜AC、BD之间练习舞蹈,她在每个平面镜中都能看到自己的一列身形,且越来越小.若AC、BD都垂直于地面,AB=6米.试问:
(1)小华在每个平面镜中看到的第二个身形之间的距离是多少?
(2)猜想小华在每个平面镜中的第10个身形之间的距离是多少米?并说明理由.
13.1 轴对称
参考答案与试题解析
一.选择题(共15小题)
1.A
2.B
3.C
4.D
5.D
6.A
7.A
8.C
9.D
10.C
11.B
12.A
13.A
14.D
15.A
二.填空题(共10小题)
16. 3 .
17. 4
18. 1
19. 200
20. 9.6 .
21. 70° .
22. 3
23. 808 .
24. WL027 .
25. TAXI .
三.解答题(共5小题)
26.解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
(2)∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(3)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(2)可知,DA=DB,FA=FC,
∴BC=DB+DF=FC=DA+DF+FA=20.
27.如图所示,沿对角线所在直线为对称轴对折,发现正方形对称位置上两数的和都为30,共10个30,对称轴上共5个15,所以所有数据的和为10×30+15×5=375.
28.解:(1)∵点P关于OA,OB的轴对称点分别为C、D,连接CD,交OA于M,交OB于N,
∴PM=CM,ND=NP,
∵△PMN的周长=PN+PM+MN,PN+PM+MN=CD=18cm,
∴△PMN的周长=18cm;
(2)点P关于OA、OB轴对称的对称点分别为C、D
所以∠C=∠CPM=21°,∠D=∠DPN=28°,
所以∠MPN=∠CPD﹣CPM﹣∠DPN=131°﹣21°﹣28°=82°.
29.如图,在4×4的正方形网格中,有5个黑色小正方形.
(1)请你移动一个黑色小正方形,使移动后所形成的4×4的正方形网格图形是轴对称图形.如:将8号小正方形移至14号;你的另一种做法是将 9 号小正方形移至 3 号(填写标号即可);
(2)请你移动2个小正方形,使移动后所形成的图形是轴对称图形,你的一种做法是将 9 号小正方形移至 3 号、将 13 号小正方形移至 4 号(填写标号即可).
30.解:(1)利用平面镜的对称性得出,每个平面镜中看到的第一个身形之间的距离是A′B′=2AB=12m,
每个平面镜中看到的第二个身形之间的距离是:4AB=24m,
答:小华在每个平面镜中看到的第二个身形之间的距离是24m,
(2)根据(1)所求即可得出:
第一个身形之间的距离是A′B′=2AB=2×6=12m,
第二个身形之间的距离是:4AB=4×6=22×6=24m,
第三个身形之间的距离是:8×6=23×6=48,
…
小华在每个平面镜中的第10个身形之间的距离是:6×210=6144m,
答:小华在每个平面镜中的第10个身形之间的距离是6144米.
日期:2020/9/9 9:59:02;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
13.1 轴对称
一.选择题(共15小题)
1.若P是△ABC所在平面内的点,且PA=PB=PC,则下列说法正确的是( )
A.点P是△ABC三边垂直平分线的交点
B.点P是△ABC三条角平分线的交点
C.点P是△ABC三边上高的交点
D.点P是△ABC三边中线的交点
2.如图,在△ABC中,AB=13,AC=12,BC=5,AB的垂直平分线分别与AB、AC交于点D、点E,那么△BCE的周长等于( )
A.25 B.17 C.18 D.以上都不对
3.如图,在Rt△ABC中,∠C=90°,作AB的垂直平分线,交AB于点D,交AC于点E,若BC=4,CE=3,则AE的长是( )
A.3 B.4 C.5 D.6
4.如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
A.(5,3) B.(3,5) C.(0,2) D.(2,0)
5.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形DABC的边时反弹,反弹时反射角等于入射角,当小球第1次磁到正方形的边时的点为P1(﹣2,0),第2次碰到正方形的边时的点为P2,…,第n次碰到正方形的边时的点为Pn,则点P2019的坐标是( )
A.(0,1) B.(﹣4,1) C.(﹣2,0) D.(0,3)
6.如图是一个经过改造的规则为3×5的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋
7.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20° C.30° D.40°
8.如图,△ABC中,D点在BC上,∠B=62°,∠C=53°,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.则∠EAF的度数为( )
A.124° B.115° C.130° D.106°
9.如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
A.30° B.50° C.90° D.100°
10.下面图标中,是轴对称图形的是( )
A. B.
C. D.
11.如图六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠DCF=150°,则∠AFE+∠BCD的大小是( )
A.150° B.300° C.210° D.330°
12.下列图形中一定是轴对称图形的是( )
A. B.
C. D.
13.如图是小明在镜子中看到的钟表的图象,此时的真实时间是( )
A.4:40 B.4:20 C.7:40 D.7:20
14.如图,一艘轮船停在平静的湖面上,则这艘轮船在湖中的倒影是( )
A. B.
C. D.
15.小明照镜子的时候,发现T恤上的英文单词在镜子中呈现的样子是( )
A. B. C. D.
二.填空题(共10小题)
16.如图,在△ABC中,AC=4,线段AB的垂直平分线交AB于点M,交AC于点N,若△BCN的周长为7,则BC= .
17.如图,在△ABC中,∠ACB=90°,∠B=22.5°,DE垂直平分AB,交BC于点E,BE=8cm,则AC等于 cm.
18.如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入 号球袋.
19.在日常生活中,你会注意到有一些含有特殊数字规律的车牌号码,如:浙A80808,浙A22222,浙A12321等,这些牌照中的五个数字都是关于中间的一个数字“对称”的,给人以对称美的感受,我们不妨把这样的牌照叫做“数字对称”牌照.如果让你负责制作只以8或9开头且有5个数字的“数字对称”牌照,那么最多可制作 个.
20.如图,△ABC中,∠ACB=90°,BC=6,AC=8,AB=10,动点P在边AB上运动(不与端点重合),点P关于直线AC,BC对称的点分别为P1,P2.则在点P的运动过程中,线段P1P2的长的最小值是 .
21.如图,∠MON内有一点P,点P关于OM的轴对称点是G,点P关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=35°,则∠GOH= .
22.如图,3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有 个.
23.下列四个图案中,具有一个共有的性质,那么在222,606,808,609下面四个数中,满足上述性质的一个是 .
24.一个汽车牌照号码在水中的倒影为,则该车牌照号码为 .
25.在上学的路上,小刚从电瓶车的后视镜里看到一辆汽车,车顶字牌上的字在平面镜中的像是IXAT,则这辆车车顶字牌上的字实际是 .
三.解答题(共5小题)
26.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)直接写出∠BAC的度数;
(2)求∠DAF的度数,并注明推导依据;
(3)若△DAF的周长为20,求BC的长.
27.小惠同学学习了轴对称知识后,忽然想起了过去做过的一道题:有一组数排列成方阵,如图所示,试计算这组数的和,小惠想方阵就像小正方形,正方形是轴对称图形,能不能利用轴对称的思想来解决方阵的问题呢?小惠试了试,竟得到了非常巧妙的方法.请你试试看!
28.如图,点P关于OA、OB轴对称的对称点分别为C、D,连结CD,交OA于M,交OB于N.
(1)若CD的长为18厘米,求△PMN的周长;
(2)若∠CPD=131°,∠C=21°,∠D=28°,求∠MPN.
29.如图,在4×4的正方形网格中,有5个黑色小正方形.
(1)请你移动一个黑色小正方形,使移动后所形成的4×4的正方形网格图形是轴对称图形.如:将8号小正方形移至14号;你的另一种做法是将 号小正方形移至 号(填写标号即可);
(2)请你移动2个小正方形,使移动后所形成的图形是轴对称图形,你的一种做法是将 号小正方形移至 号、将 号小正方形移至 号(填写标号即可).
30.舞蹈教室的东西墙壁有平面镜AC、BD,如图小华在平面镜AC、BD之间练习舞蹈,她在每个平面镜中都能看到自己的一列身形,且越来越小.若AC、BD都垂直于地面,AB=6米.试问:
(1)小华在每个平面镜中看到的第二个身形之间的距离是多少?
(2)猜想小华在每个平面镜中的第10个身形之间的距离是多少米?并说明理由.
13.1 轴对称
参考答案与试题解析
一.选择题(共15小题)
1.A
2.B
3.C
4.D
5.D
6.A
7.A
8.C
9.D
10.C
11.B
12.A
13.A
14.D
15.A
二.填空题(共10小题)
16. 3 .
17. 4
18. 1
19. 200
20. 9.6 .
21. 70° .
22. 3
23. 808 .
24. WL027 .
25. TAXI .
三.解答题(共5小题)
26.解:(1)∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣30°﹣50°=100°;
(2)∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30°,
同理可得,∠FAC=∠ACB=50°,
∴∠DAF=∠BAC﹣∠DAB﹣∠FAC=100°﹣30°﹣50°=20°;
(3)∵△DAF的周长为20,
∴DA+DF+FA=20,
由(2)可知,DA=DB,FA=FC,
∴BC=DB+DF=FC=DA+DF+FA=20.
27.如图所示,沿对角线所在直线为对称轴对折,发现正方形对称位置上两数的和都为30,共10个30,对称轴上共5个15,所以所有数据的和为10×30+15×5=375.
28.解:(1)∵点P关于OA,OB的轴对称点分别为C、D,连接CD,交OA于M,交OB于N,
∴PM=CM,ND=NP,
∵△PMN的周长=PN+PM+MN,PN+PM+MN=CD=18cm,
∴△PMN的周长=18cm;
(2)点P关于OA、OB轴对称的对称点分别为C、D
所以∠C=∠CPM=21°,∠D=∠DPN=28°,
所以∠MPN=∠CPD﹣CPM﹣∠DPN=131°﹣21°﹣28°=82°.
29.如图,在4×4的正方形网格中,有5个黑色小正方形.
(1)请你移动一个黑色小正方形,使移动后所形成的4×4的正方形网格图形是轴对称图形.如:将8号小正方形移至14号;你的另一种做法是将 9 号小正方形移至 3 号(填写标号即可);
(2)请你移动2个小正方形,使移动后所形成的图形是轴对称图形,你的一种做法是将 9 号小正方形移至 3 号、将 13 号小正方形移至 4 号(填写标号即可).
30.解:(1)利用平面镜的对称性得出,每个平面镜中看到的第一个身形之间的距离是A′B′=2AB=12m,
每个平面镜中看到的第二个身形之间的距离是:4AB=24m,
答:小华在每个平面镜中看到的第二个身形之间的距离是24m,
(2)根据(1)所求即可得出:
第一个身形之间的距离是A′B′=2AB=2×6=12m,
第二个身形之间的距离是:4AB=4×6=22×6=24m,
第三个身形之间的距离是:8×6=23×6=48,
…
小华在每个平面镜中的第10个身形之间的距离是:6×210=6144m,
答:小华在每个平面镜中的第10个身形之间的距离是6144米.
日期:2020/9/9 9:59:02;用户:40中金山分校;邮箱:40zjs@xyh.com;学号:37582644
_21?????????è?????(www.21cnjy.com)_
