13.2 画轴对称图形同步练习(含答案)
文档属性
| 名称 | 13.2 画轴对称图形同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 232.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 19:12:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
13.2 画轴对称图形
一.选择题(共9小题)
1.在平面直角坐标系中,点M(12,﹣17)关于x轴对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若直线a经过(0,9),直线b经过(4,3),且a与b关于x轴对称,则a与b的交点的坐标为( )
A.(3,0) B.(2,0) C.(﹣3,0) D.(﹣2,0)
3.在平面直角坐标系中,将点P(﹣3,2)向右平移3个单位得到点P',则点P'关于x轴的对称点的坐标为( )
A.(0,﹣2) B.(0,2) C.(﹣6,2) D.(﹣6,﹣2)
4.在平面直角坐标系上,已知点A关于直线x=1对称的点为B(﹣2,4),则点A的坐标为( )
A.(4,4) B.(﹣2,﹣2) C.(2,4) D.(3,4)
5.如图,已知平行四边形OABC的顶点O(0,0),B(2,2),C(1.6,0.8).若将平行四边形先沿着y轴进行第一次轴对称变换,所得图形再沿着x轴进行第二次轴对称变换,轴对称变换的对称轴遵循y轴、x轴、y轴、x轴…的规律进行,则经过第2018次变换后,平行四边形顶点A的坐标为( )
A.(﹣0.4,1.2) B.(﹣0.4,﹣1.2)
C.(1.2,﹣0.4) D.(﹣1.2,﹣0.4)
6.在平面直角坐标系中,点P(0,1)关于直线x=﹣1的对称点坐标是( )
A.(﹣2,1) B.(2,1) C.(0,﹣1) D.(0,1)
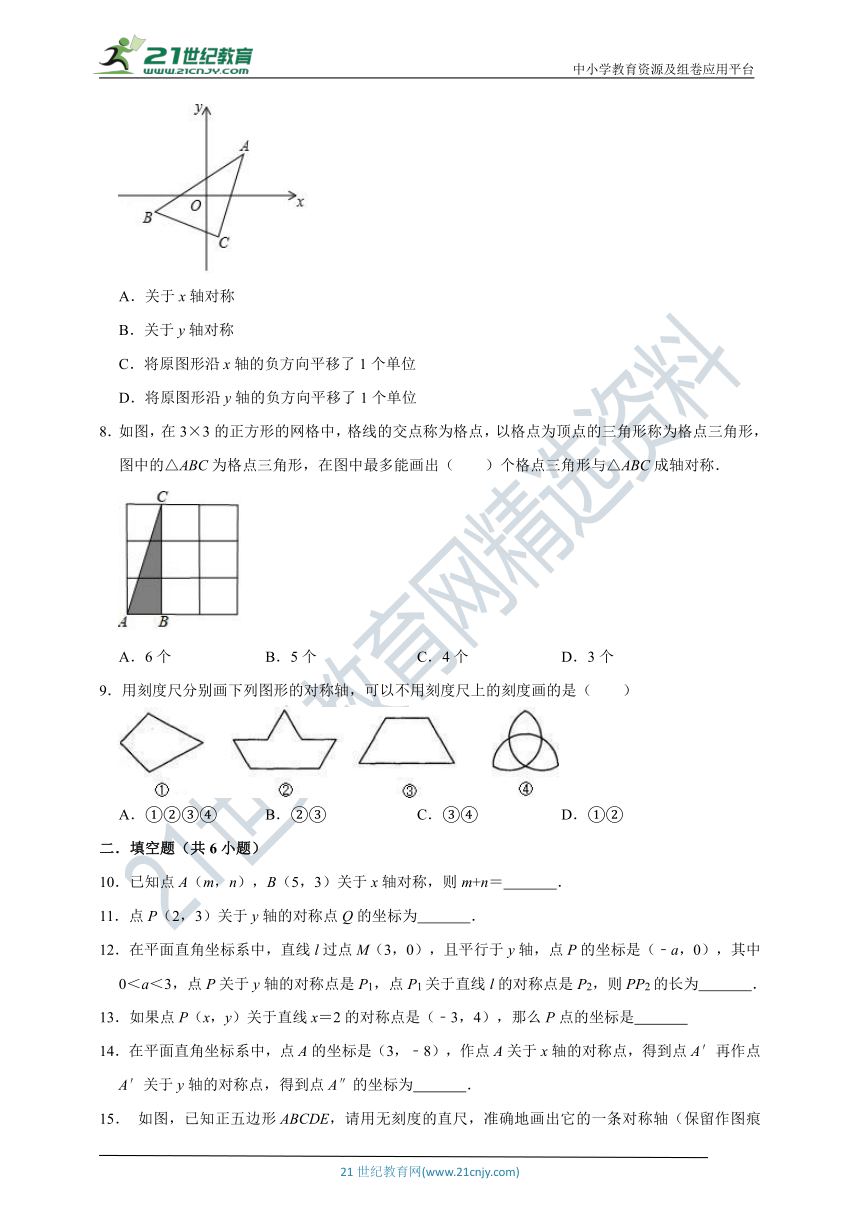
7.如图,保持△ABC的三个顶点的横坐标不变,纵坐标都乘﹣1,画出坐标变化后的三角形,则所得三角形与原三角形的关系是( )
A.关于x轴对称
B.关于y轴对称
C.将原图形沿x轴的负方向平移了1个单位
D.将原图形沿y轴的负方向平移了1个单位
8.如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
A.6个 B.5个 C.4个 D.3个
9.用刻度尺分别画下列图形的对称轴,可以不用刻度尺上的刻度画的是( )
A.①②③④ B.②③ C.③④ D.①②
二.填空题(共6小题)
10.已知点A(m,n),B(5,3)关于x轴对称,则m+n= .
11.点P(2,3)关于y轴的对称点Q的坐标为 .
12.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴,点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,则PP2的长为 .
13.如果点P(x,y)关于直线x=2的对称点是(﹣3,4),那么P点的坐标是
14.在平面直角坐标系中,点A的坐标是(3,﹣8),作点A关于x轴的对称点,得到点A′再作点A′关于y轴的对称点,得到点A″的坐标为 .
15. 如图,已知正五边形ABCDE,请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹). .
三.解答题(共3小题)
16.已知点A(a+2b,1),B(7,a﹣2b).
(1)如果点A、B关于x轴对称,求a、b的值;
(2)如果点A、B关于y轴对称,求a、b的值.
17.如图,在平面直角坐标系xOy中,△ABC的三个顶点分别落在边长为1的正方形格上,
(Ⅰ)分别写出A、B、C三点坐标;
(Ⅱ)△DEF可以看作是△ABC经过若干次的图形变化(轴对称、平移)得到的,写出一种由△ABC得到△DEF的过程,并体现在坐标系中.
18.如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,点A,点C在直线a上.
(1)作△ABC关于直线a的轴对称图形△ADC;
(2)若∠BAC=35°,则∠BDA= ;
(3)求△ABD的面积.
13.2 画轴对称图形
参考答案与试题解析
一.选择题(共9小题)
1.A
2.A
3.A
4.A
5.B
6.A
7.A
8.A
9.A
二.填空题(共6小题)
10. 2 .
11. (﹣2,3) .
12. 6 .
13. (7,4)
14.(﹣3,8) .
15. .
三.解答题(共3小题)
16.解:(1)∵点A、B关于x轴对称,
∴,
解得:;
(2))∵点A、B关于y轴对称,
∴,
解得:.
17.解:(Ⅰ)由图象可得:点A(0,﹣1),点B(2,﹣1),点C(2,﹣2);
(Ⅱ)先将△ABC沿y轴翻折,得到△AB'C',再将△AB'C'向上平移3个单位可得△DEF.
(1)作△ABC关于直线a的轴对称图形△ADC;
(2) 55° ;
(3)求△ABD的面积.
(3)△ABD的面积=×10×7=35.
_21?????????è?????(www.21cnjy.com)_
13.2 画轴对称图形
一.选择题(共9小题)
1.在平面直角坐标系中,点M(12,﹣17)关于x轴对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若直线a经过(0,9),直线b经过(4,3),且a与b关于x轴对称,则a与b的交点的坐标为( )
A.(3,0) B.(2,0) C.(﹣3,0) D.(﹣2,0)
3.在平面直角坐标系中,将点P(﹣3,2)向右平移3个单位得到点P',则点P'关于x轴的对称点的坐标为( )
A.(0,﹣2) B.(0,2) C.(﹣6,2) D.(﹣6,﹣2)
4.在平面直角坐标系上,已知点A关于直线x=1对称的点为B(﹣2,4),则点A的坐标为( )
A.(4,4) B.(﹣2,﹣2) C.(2,4) D.(3,4)
5.如图,已知平行四边形OABC的顶点O(0,0),B(2,2),C(1.6,0.8).若将平行四边形先沿着y轴进行第一次轴对称变换,所得图形再沿着x轴进行第二次轴对称变换,轴对称变换的对称轴遵循y轴、x轴、y轴、x轴…的规律进行,则经过第2018次变换后,平行四边形顶点A的坐标为( )
A.(﹣0.4,1.2) B.(﹣0.4,﹣1.2)
C.(1.2,﹣0.4) D.(﹣1.2,﹣0.4)
6.在平面直角坐标系中,点P(0,1)关于直线x=﹣1的对称点坐标是( )
A.(﹣2,1) B.(2,1) C.(0,﹣1) D.(0,1)
7.如图,保持△ABC的三个顶点的横坐标不变,纵坐标都乘﹣1,画出坐标变化后的三角形,则所得三角形与原三角形的关系是( )
A.关于x轴对称
B.关于y轴对称
C.将原图形沿x轴的负方向平移了1个单位
D.将原图形沿y轴的负方向平移了1个单位
8.如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
A.6个 B.5个 C.4个 D.3个
9.用刻度尺分别画下列图形的对称轴,可以不用刻度尺上的刻度画的是( )
A.①②③④ B.②③ C.③④ D.①②
二.填空题(共6小题)
10.已知点A(m,n),B(5,3)关于x轴对称,则m+n= .
11.点P(2,3)关于y轴的对称点Q的坐标为 .
12.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴,点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,则PP2的长为 .
13.如果点P(x,y)关于直线x=2的对称点是(﹣3,4),那么P点的坐标是
14.在平面直角坐标系中,点A的坐标是(3,﹣8),作点A关于x轴的对称点,得到点A′再作点A′关于y轴的对称点,得到点A″的坐标为 .
15. 如图,已知正五边形ABCDE,请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹). .
三.解答题(共3小题)
16.已知点A(a+2b,1),B(7,a﹣2b).
(1)如果点A、B关于x轴对称,求a、b的值;
(2)如果点A、B关于y轴对称,求a、b的值.
17.如图,在平面直角坐标系xOy中,△ABC的三个顶点分别落在边长为1的正方形格上,
(Ⅰ)分别写出A、B、C三点坐标;
(Ⅱ)△DEF可以看作是△ABC经过若干次的图形变化(轴对称、平移)得到的,写出一种由△ABC得到△DEF的过程,并体现在坐标系中.
18.如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,点A,点C在直线a上.
(1)作△ABC关于直线a的轴对称图形△ADC;
(2)若∠BAC=35°,则∠BDA= ;
(3)求△ABD的面积.
13.2 画轴对称图形
参考答案与试题解析
一.选择题(共9小题)
1.A
2.A
3.A
4.A
5.B
6.A
7.A
8.A
9.A
二.填空题(共6小题)
10. 2 .
11. (﹣2,3) .
12. 6 .
13. (7,4)
14.(﹣3,8) .
15. .
三.解答题(共3小题)
16.解:(1)∵点A、B关于x轴对称,
∴,
解得:;
(2))∵点A、B关于y轴对称,
∴,
解得:.
17.解:(Ⅰ)由图象可得:点A(0,﹣1),点B(2,﹣1),点C(2,﹣2);
(Ⅱ)先将△ABC沿y轴翻折,得到△AB'C',再将△AB'C'向上平移3个单位可得△DEF.
(1)作△ABC关于直线a的轴对称图形△ADC;
(2) 55° ;
(3)求△ABD的面积.
(3)△ABD的面积=×10×7=35.
_21?????????è?????(www.21cnjy.com)_
