最大面积是多少(1)二次函数的应用
图片预览



文档简介
(共15张PPT)
九年级数学(下)第二章
二次函数
7. 最大面积是多少(1)二次函数的应用
(1).设矩形的一边AB=xcm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
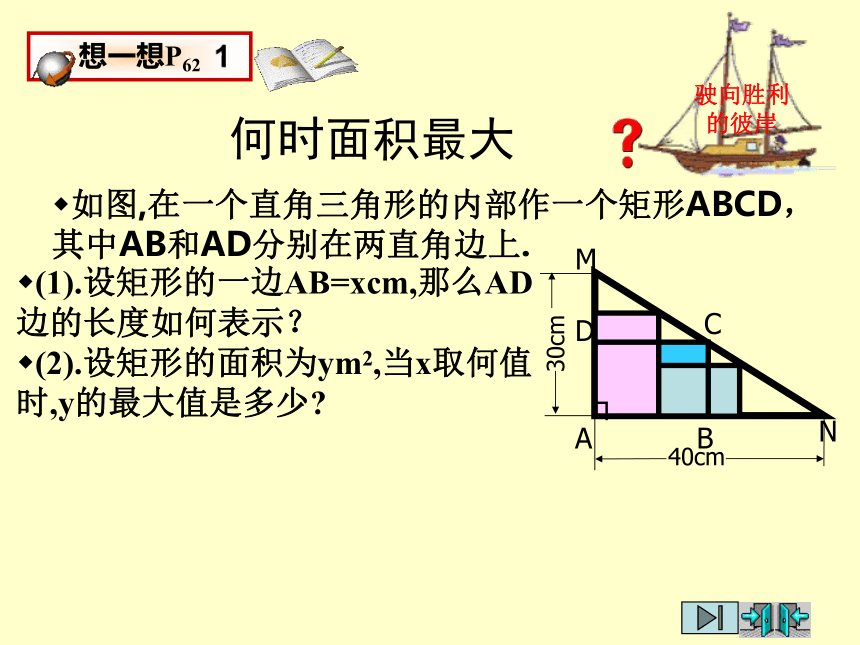
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
想一想P62
1
驶向胜利的彼岸
M
N
40cm
30cm
A
B
C
D
┐
(1).设矩形的一边AB=xcm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
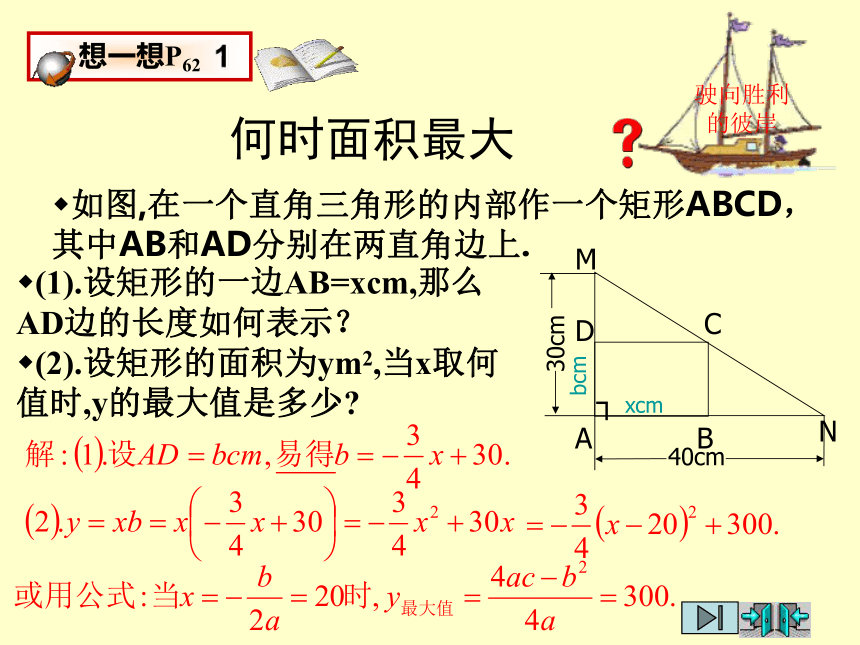
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
想一想P62
1
驶向胜利的彼岸
A
B
C
D
┐
M
N
40cm
30cm
xcm
bcm
(1).如果设矩形的一边AD=xcm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
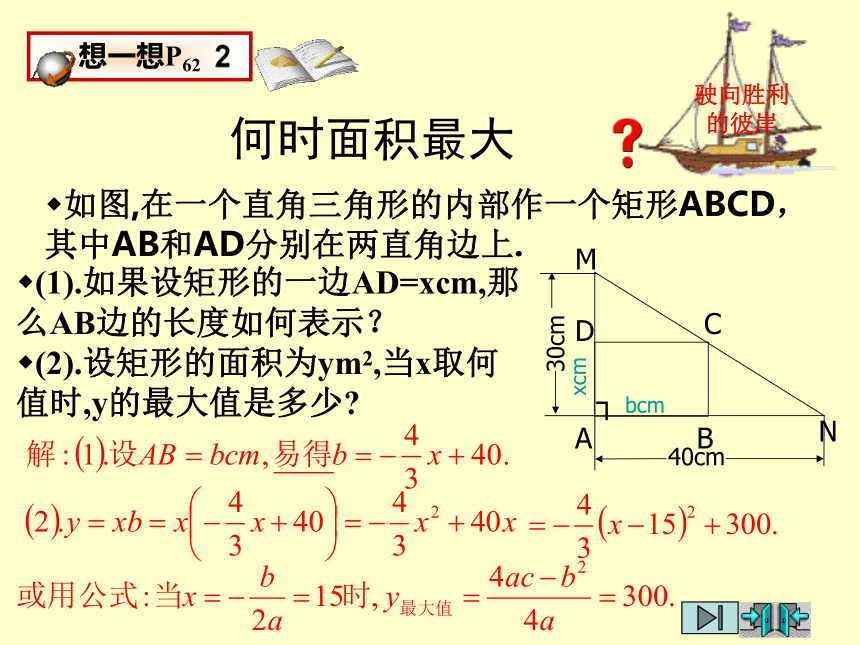
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
想一想P62
2
驶向胜利的彼岸
A
B
C
D
┐
M
N
40cm
30cm
bcm
xcm
(1).设矩形的一边BC=xcm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
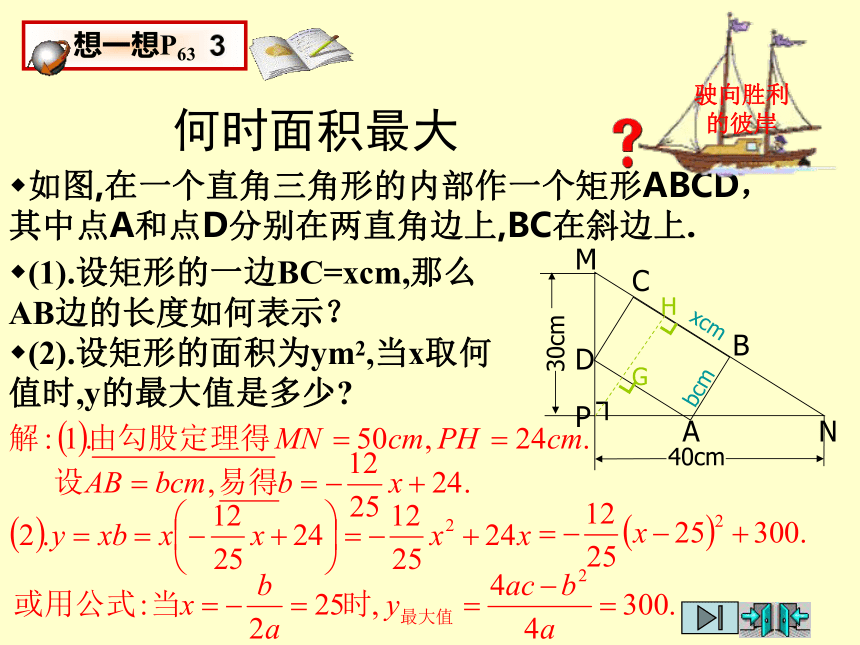
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中点A和点D分别在两直角边上,BC在斜边上.
想一想P63
3
驶向胜利的彼岸
A
B
C
D
┐
M
N
P
40cm
30cm
xcm
bcm
H
G
┛
┛
何时窗户通过的光线最多
某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m) 此时,窗户的面积是多少
做一做P62
5
驶向胜利的彼岸
x
x
y
专题:卡车过桥问题
1.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用y=-
x2+4表示。
(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?
(2)如果隧道内设双行道,那么这辆货运车是否可以通过?
A
图4
.如图4,有一座抛物线形拱桥,抛物线可用y= 表示.在正常水位时水面AB 的宽为20m,如果水位上升3m水面CD的宽是10m.
(1)在正常水位时,有一艘宽8m、高2.5m的小船,
它能通过这座桥吗
2.现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时, 忽然接到紧急通过:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行).
试问:如果货车按原来的速度行驶,能否安全通过此桥 若能,请说明理由.若不能, 要使货车安全通过此桥,速度应超过每小时多少千米
图4
如图在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,已知AC=1,AB=2,求:(1)何时矩形PMCN的面积最大,把最大面积是多少?
(2)当AM平分∠CAB时,矩形PMCN的面积.
拟建中的一个温室的平面图如图,如果温室外围是一个矩形,周长为120m , 室内通道的尺寸如图,设一条边长为 x (cm), 种植面积为 y (m2)。试建立y与x的函数关系式,并当x取何值时,种植面积最大?最大面积是多少?
如图,用长20cm的篱笆,一面靠墙围成一个长方形的园子,怎样围才能使园子的面积最大?最大面积是多少?
1.理解问题;
“二次函数应用” 的思路
回顾上一节“最大利润”和本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
议一议P63
4
驶向胜利的彼岸
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性,拓展等.
寄语
不知道并不可怕和有害,任何人都不可能什么都知道,可怕的和有害的是不知道而伪装知道.
九年级数学(下)第二章
二次函数
7. 最大面积是多少(1)二次函数的应用
(1).设矩形的一边AB=xcm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
想一想P62
1
驶向胜利的彼岸
M
N
40cm
30cm
A
B
C
D
┐
(1).设矩形的一边AB=xcm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
想一想P62
1
驶向胜利的彼岸
A
B
C
D
┐
M
N
40cm
30cm
xcm
bcm
(1).如果设矩形的一边AD=xcm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
想一想P62
2
驶向胜利的彼岸
A
B
C
D
┐
M
N
40cm
30cm
bcm
xcm
(1).设矩形的一边BC=xcm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中点A和点D分别在两直角边上,BC在斜边上.
想一想P63
3
驶向胜利的彼岸
A
B
C
D
┐
M
N
P
40cm
30cm
xcm
bcm
H
G
┛
┛
何时窗户通过的光线最多
某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m) 此时,窗户的面积是多少
做一做P62
5
驶向胜利的彼岸
x
x
y
专题:卡车过桥问题
1.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用y=-
x2+4表示。
(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?
(2)如果隧道内设双行道,那么这辆货运车是否可以通过?
A
图4
.如图4,有一座抛物线形拱桥,抛物线可用y= 表示.在正常水位时水面AB 的宽为20m,如果水位上升3m水面CD的宽是10m.
(1)在正常水位时,有一艘宽8m、高2.5m的小船,
它能通过这座桥吗
2.现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时, 忽然接到紧急通过:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行).
试问:如果货车按原来的速度行驶,能否安全通过此桥 若能,请说明理由.若不能, 要使货车安全通过此桥,速度应超过每小时多少千米
图4
如图在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,已知AC=1,AB=2,求:(1)何时矩形PMCN的面积最大,把最大面积是多少?
(2)当AM平分∠CAB时,矩形PMCN的面积.
拟建中的一个温室的平面图如图,如果温室外围是一个矩形,周长为120m , 室内通道的尺寸如图,设一条边长为 x (cm), 种植面积为 y (m2)。试建立y与x的函数关系式,并当x取何值时,种植面积最大?最大面积是多少?
如图,用长20cm的篱笆,一面靠墙围成一个长方形的园子,怎样围才能使园子的面积最大?最大面积是多少?
1.理解问题;
“二次函数应用” 的思路
回顾上一节“最大利润”和本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
议一议P63
4
驶向胜利的彼岸
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性,拓展等.
寄语
不知道并不可怕和有害,任何人都不可能什么都知道,可怕的和有害的是不知道而伪装知道.
