14.2.1 平方差公式同步练习(含答案)
文档属性
| 名称 | 14.2.1 平方差公式同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 196.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 19:43:43 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
14.2.2 平方差公式
一.平方差公式(共6小题)
1.下列数量关系中,用式子表示的结果为单项式的是( )
A.a与b的平方差
B.a与x的2倍的差的相反数
C.比a的倒数大11的数
D.a的2倍的相反数与y的积
2.下面有4道题,小明在横线上面写出了答案:①(a+b)(b﹣a)=﹣a2+b2,②(﹣a5)÷(﹣a)2=﹣a3,③32019×()2020=3,④若a﹣b=2,则a2﹣b2﹣4b=4.他写对答案的题是( )
A.①② B.①②③ C.①②④ D.②③④
3.下列多项式的乘法中,不能用平方差公式计算的是( )
A.(4x﹣3y)(﹣3y﹣4x) B.(x﹣y)(﹣x+y)
C.(a+b﹣c)(a﹣b+c) D.(2x2﹣y2)(2x2+y2)
4.若m2﹣n2=5,则(m+n)2?(m﹣n)2的值是 .
5.计算2021×2019﹣20202的值为 .
6.化简:(x﹣2y﹣z)(x+2y﹣z)﹣(x+z)2.
二.平方差公式的几何背景(共6小题)
7.如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( )
A.(m﹣n)2=m2﹣2mn+n2 B.(m+n)2=m2+2mn+n2
C.(m﹣n)2=m2+n2 D.m2﹣n2=(m+n)(m﹣n)
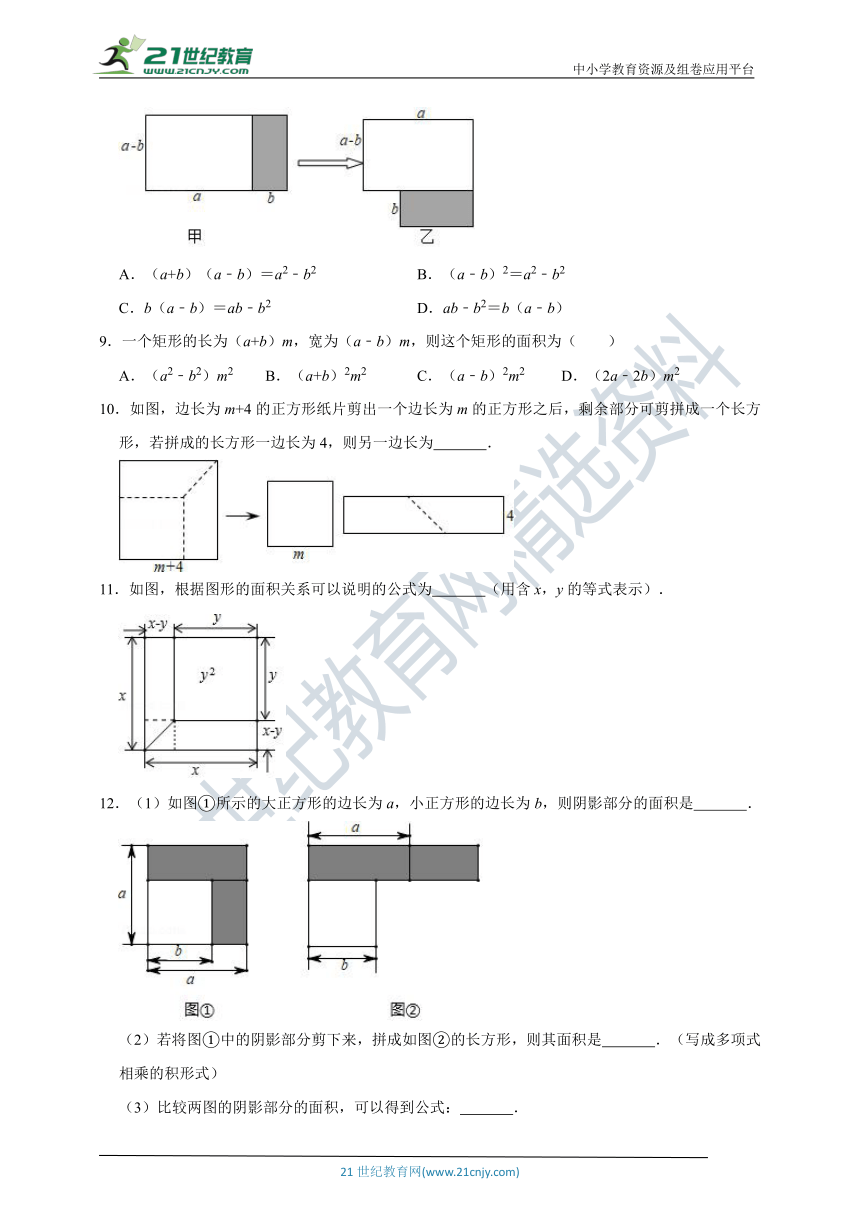
8.将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.(a﹣b)2=a2﹣b2
C.b(a﹣b)=ab﹣b2 D.ab﹣b2=b(a﹣b)
9.一个矩形的长为(a+b)m,宽为(a﹣b)m,则这个矩形的面积为( )
A.(a2﹣b2)m2 B.(a+b)2m2 C.(a﹣b)2m2 D.(2a﹣2b)m2
10.如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为4,则另一边长为 .
11.如图,根据图形的面积关系可以说明的公式为 (用含x,y的等式表示).
12.(1)如图①所示的大正方形的边长为a,小正方形的边长为b,则阴影部分的面积是 .
(2)若将图①中的阴影部分剪下来,拼成如图②的长方形,则其面积是 .(写成多项式相乘的积形式)
(3)比较两图的阴影部分的面积,可以得到公式: .
(4)应用公式计算:(1﹣)(1﹣)(1﹣).
14.2.2 平方差公式参考答案
一.平方差公式(共6小题)
1.D
2.C
3.B
4. 25 .
5. ﹣1 .
6.解:原式=(x﹣z)2﹣(2y)2﹣(x+z)2
=(x﹣z)2﹣(x+z)2﹣(2y)2
=(x﹣z+x+z)(x﹣z﹣x﹣z)﹣(2y)2
=﹣4xz﹣4y2.
二.平方差公式的几何背景(共6小题)
7.D
8.A
9.A
10. 2m+4 .
11. x2﹣y2=(x+y)(x﹣y)
12.(1) a2﹣b2 .
(2) (a+b)(a﹣b)
(3) (a﹣b)(a+b)=a2﹣b2 .
(4)(1﹣)(1﹣)(1﹣)
=
=
=
=.
_21?????????è?????(www.21cnjy.com)_
14.2.2 平方差公式
一.平方差公式(共6小题)
1.下列数量关系中,用式子表示的结果为单项式的是( )
A.a与b的平方差
B.a与x的2倍的差的相反数
C.比a的倒数大11的数
D.a的2倍的相反数与y的积
2.下面有4道题,小明在横线上面写出了答案:①(a+b)(b﹣a)=﹣a2+b2,②(﹣a5)÷(﹣a)2=﹣a3,③32019×()2020=3,④若a﹣b=2,则a2﹣b2﹣4b=4.他写对答案的题是( )
A.①② B.①②③ C.①②④ D.②③④
3.下列多项式的乘法中,不能用平方差公式计算的是( )
A.(4x﹣3y)(﹣3y﹣4x) B.(x﹣y)(﹣x+y)
C.(a+b﹣c)(a﹣b+c) D.(2x2﹣y2)(2x2+y2)
4.若m2﹣n2=5,则(m+n)2?(m﹣n)2的值是 .
5.计算2021×2019﹣20202的值为 .
6.化简:(x﹣2y﹣z)(x+2y﹣z)﹣(x+z)2.
二.平方差公式的几何背景(共6小题)
7.如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( )
A.(m﹣n)2=m2﹣2mn+n2 B.(m+n)2=m2+2mn+n2
C.(m﹣n)2=m2+n2 D.m2﹣n2=(m+n)(m﹣n)
8.将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.(a﹣b)2=a2﹣b2
C.b(a﹣b)=ab﹣b2 D.ab﹣b2=b(a﹣b)
9.一个矩形的长为(a+b)m,宽为(a﹣b)m,则这个矩形的面积为( )
A.(a2﹣b2)m2 B.(a+b)2m2 C.(a﹣b)2m2 D.(2a﹣2b)m2
10.如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为4,则另一边长为 .
11.如图,根据图形的面积关系可以说明的公式为 (用含x,y的等式表示).
12.(1)如图①所示的大正方形的边长为a,小正方形的边长为b,则阴影部分的面积是 .
(2)若将图①中的阴影部分剪下来,拼成如图②的长方形,则其面积是 .(写成多项式相乘的积形式)
(3)比较两图的阴影部分的面积,可以得到公式: .
(4)应用公式计算:(1﹣)(1﹣)(1﹣).
14.2.2 平方差公式参考答案
一.平方差公式(共6小题)
1.D
2.C
3.B
4. 25 .
5. ﹣1 .
6.解:原式=(x﹣z)2﹣(2y)2﹣(x+z)2
=(x﹣z)2﹣(x+z)2﹣(2y)2
=(x﹣z+x+z)(x﹣z﹣x﹣z)﹣(2y)2
=﹣4xz﹣4y2.
二.平方差公式的几何背景(共6小题)
7.D
8.A
9.A
10. 2m+4 .
11. x2﹣y2=(x+y)(x﹣y)
12.(1) a2﹣b2 .
(2) (a+b)(a﹣b)
(3) (a﹣b)(a+b)=a2﹣b2 .
(4)(1﹣)(1﹣)(1﹣)
=
=
=
=.
_21?????????è?????(www.21cnjy.com)_
