高中物理教科版1.6 匀变速直线运动位移与时间的关系
文档属性
| 名称 | 高中物理教科版1.6 匀变速直线运动位移与时间的关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
数形结合解决物理问题
6
匀变速直线运动位移与时间的关系
v
t
1
匀速直线运动位移
公式法
图像法
方法一:
x=vt
结论:
匀速直线运动的位移对应着v-t
图线与t轴所夹的矩形“面积”。
方法二:
面积
数学方法解决物理问题
面积
3
4
5
6
2
1
v/m·s-1
t/s
2
6
4
10
8
0
-2
-4
1
匀速直线运动位移
甲
x
乙
x甲
x乙
特别提醒:
位移也有正负,
t
轴上方,表示位移的方向为正方向,
t
轴下方,表示位移的方向为负方向。
t
轴上下的位移有何区别?
匀变速直线运动的位移与它的v-t图象是否也有类似的关系?
思考?
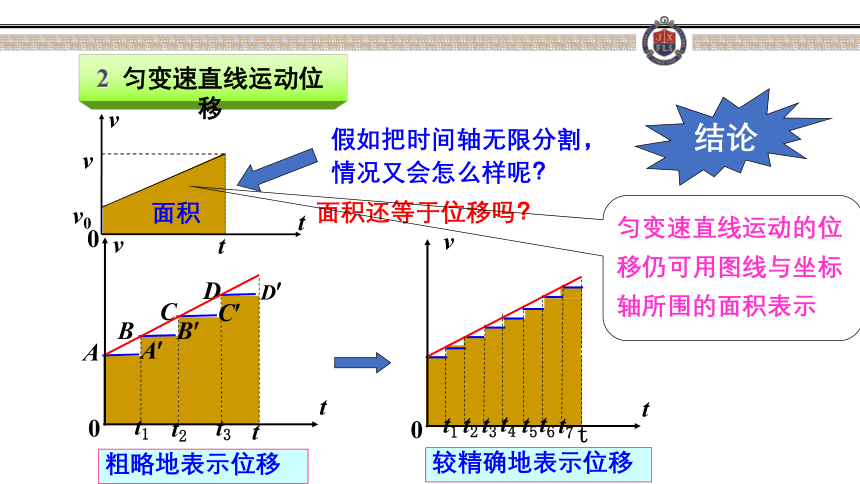
2
匀变速直线运动位移
A
A?
B?
B
C
C?
D
D?
粗略地表示位移
较精确地表示位移
?
v
t
0
t
t1
t2
t3
v
t
0
t
t1
t2
t3
t4
t5
t6
t7
假如把时间轴无限分割,情况又会怎么样呢?
面积
面积还等于位移吗?
v
t
v0
v
t
0
匀变速直线运动的位移仍可用图线与坐标轴所围的面积表示
结论
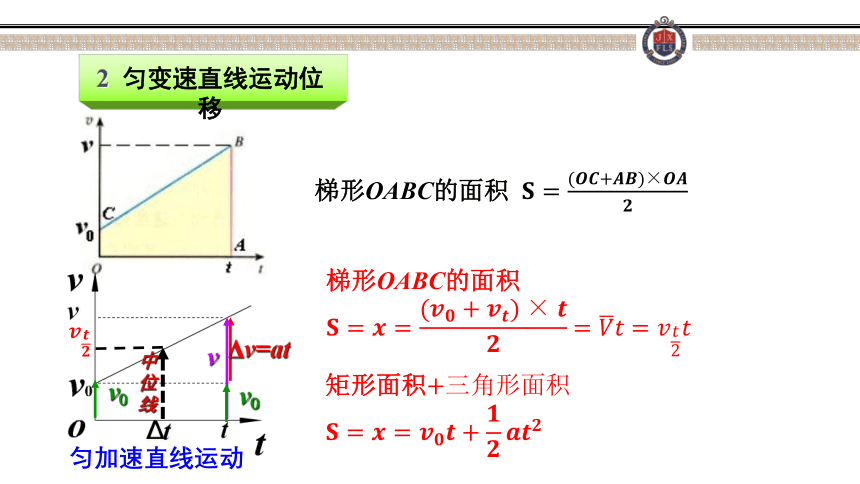
2
匀变速直线运动位移
t
v
匀加速直线运动
v0
Δv=at
v
v0
Δt
中位线
梯形OABC的面积
梯形OABC的面积
矩形面积
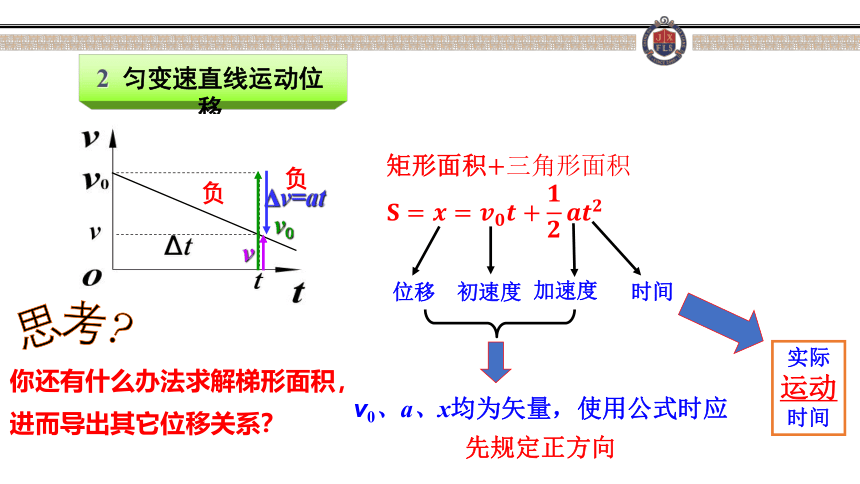
2
匀变速直线运动位移
v
t
Δt
v0
Δv=at
v
矩形面积
负
负
位移
初速度
加速度
时间
v0、a、x均为矢量,使用公式时应先规定正方向
实际运动时间
你还有什么办法求解梯形面积,进而导出其它位移关系?
思考?
3
例题分析
例1.一辆汽车以1m/s2的加速度加速行驶了12s,驶过了180m。汽车开始加速时的速度是多少?
解:汽车向右加速运动
解得:
3
例题分析
例2:在平直公路上,一汽车的速度为16m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末汽车离开始刹车点多远?
解:设实际运动时间为t0
解得:t0=8s
汽车刹车后8s停止运动
解得:x=64m
解题关键:汽车刹车类问题要注意刹车停止时间问题
位移与时间的关系也可以用图像来表示,这种图像叫位移—时间图像,即x-t图像。你能画出匀变速直线运动的x-t图像的草图吗?试试看。
a为静止物体的x-t图像:
平行于时间轴的直线
b为匀速直线运动的x-t图像:
一条倾斜的直线
c为匀变速直线运动的x-t图像:
一条抛物线
t
0
x
c
a
b
3
位移—时间图像
3
例题分析
例3:物体做直线运动,其位移图象如图所示,试求:
(2)20s内的平均速度.
(3)第二个10S内的平均速度.
10
x/m
O
30
20
20
t/s
30
10
(1)5s末的瞬时速度.
3m/s
1m/s
-1m/s
小结
问题1
v-t图像与时间轴所围的面积代表什么?
问题2
位移与时间关系的表达式是什么?
问题3
从x-t图像中我们可以得到哪些信息?
4
达标训练
1.某一做直线运动的物体的v-t图象如图所示,根据图象求:
(1)物体距出发点的最远距离;
(2)前4
s内物体的位移;
(3)前4
s内物体通过的路程。
[答案] (1)6
m (2)5
m (3)7
m
4
达标训练
2.某质点沿轴运动的速度图像如图所示,则下列
判断正确的是(
)
A.第1s末运动方向发生改变
B.第2s末回到出发点
C.前3s的总位移为3m
D.第4s末回到出发点
D
【解题关键】:要明确各段图线的
(1)初速度情况;
(2)运动性质;
(3)运动时间。
4
达标训练
3.从车站开出的汽车,做匀加速直线运动,走了12s时,发现还有乘客没上来,于是立即做匀减速运动直至停车。汽车从开出到停止总共历时20s,行进了100
m。求汽车在此过程中的最大速度。
互动探究:你还能想出其他更好的解法吗?给大家露一手吧!
10m/s
4
达标训练
4.骑自行车的人以5m/s的初速度匀减速地上一个斜坡,加速度的大小为0.4m/s2,斜坡长30m,骑自行车的人通过斜坡需要多少时间?
解:骑车向上匀减速运动
解得:t1=10s,t2=15s
?
答案:t=10s
讨论:
把两个时间代入速度公式计算末速度:
v1=1m/s,v2=-1m/s
与实际情况不符,舍去!
梳理知识
及时复习
规范作业
训练思维
认真纠错
提升能力
数形结合解决物理问题
6
匀变速直线运动位移与时间的关系
v
t
1
匀速直线运动位移
公式法
图像法
方法一:
x=vt
结论:
匀速直线运动的位移对应着v-t
图线与t轴所夹的矩形“面积”。
方法二:
面积
数学方法解决物理问题
面积
3
4
5
6
2
1
v/m·s-1
t/s
2
6
4
10
8
0
-2
-4
1
匀速直线运动位移
甲
x
乙
x甲
x乙
特别提醒:
位移也有正负,
t
轴上方,表示位移的方向为正方向,
t
轴下方,表示位移的方向为负方向。
t
轴上下的位移有何区别?
匀变速直线运动的位移与它的v-t图象是否也有类似的关系?
思考?
2
匀变速直线运动位移
A
A?
B?
B
C
C?
D
D?
粗略地表示位移
较精确地表示位移
?
v
t
0
t
t1
t2
t3
v
t
0
t
t1
t2
t3
t4
t5
t6
t7
假如把时间轴无限分割,情况又会怎么样呢?
面积
面积还等于位移吗?
v
t
v0
v
t
0
匀变速直线运动的位移仍可用图线与坐标轴所围的面积表示
结论
2
匀变速直线运动位移
t
v
匀加速直线运动
v0
Δv=at
v
v0
Δt
中位线
梯形OABC的面积
梯形OABC的面积
矩形面积
2
匀变速直线运动位移
v
t
Δt
v0
Δv=at
v
矩形面积
负
负
位移
初速度
加速度
时间
v0、a、x均为矢量,使用公式时应先规定正方向
实际运动时间
你还有什么办法求解梯形面积,进而导出其它位移关系?
思考?
3
例题分析
例1.一辆汽车以1m/s2的加速度加速行驶了12s,驶过了180m。汽车开始加速时的速度是多少?
解:汽车向右加速运动
解得:
3
例题分析
例2:在平直公路上,一汽车的速度为16m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末汽车离开始刹车点多远?
解:设实际运动时间为t0
解得:t0=8s
汽车刹车后8s停止运动
解得:x=64m
解题关键:汽车刹车类问题要注意刹车停止时间问题
位移与时间的关系也可以用图像来表示,这种图像叫位移—时间图像,即x-t图像。你能画出匀变速直线运动的x-t图像的草图吗?试试看。
a为静止物体的x-t图像:
平行于时间轴的直线
b为匀速直线运动的x-t图像:
一条倾斜的直线
c为匀变速直线运动的x-t图像:
一条抛物线
t
0
x
c
a
b
3
位移—时间图像
3
例题分析
例3:物体做直线运动,其位移图象如图所示,试求:
(2)20s内的平均速度.
(3)第二个10S内的平均速度.
10
x/m
O
30
20
20
t/s
30
10
(1)5s末的瞬时速度.
3m/s
1m/s
-1m/s
小结
问题1
v-t图像与时间轴所围的面积代表什么?
问题2
位移与时间关系的表达式是什么?
问题3
从x-t图像中我们可以得到哪些信息?
4
达标训练
1.某一做直线运动的物体的v-t图象如图所示,根据图象求:
(1)物体距出发点的最远距离;
(2)前4
s内物体的位移;
(3)前4
s内物体通过的路程。
[答案] (1)6
m (2)5
m (3)7
m
4
达标训练
2.某质点沿轴运动的速度图像如图所示,则下列
判断正确的是(
)
A.第1s末运动方向发生改变
B.第2s末回到出发点
C.前3s的总位移为3m
D.第4s末回到出发点
D
【解题关键】:要明确各段图线的
(1)初速度情况;
(2)运动性质;
(3)运动时间。
4
达标训练
3.从车站开出的汽车,做匀加速直线运动,走了12s时,发现还有乘客没上来,于是立即做匀减速运动直至停车。汽车从开出到停止总共历时20s,行进了100
m。求汽车在此过程中的最大速度。
互动探究:你还能想出其他更好的解法吗?给大家露一手吧!
10m/s
4
达标训练
4.骑自行车的人以5m/s的初速度匀减速地上一个斜坡,加速度的大小为0.4m/s2,斜坡长30m,骑自行车的人通过斜坡需要多少时间?
解:骑车向上匀减速运动
解得:t1=10s,t2=15s
?
答案:t=10s
讨论:
把两个时间代入速度公式计算末速度:
v1=1m/s,v2=-1m/s
与实际情况不符,舍去!
梳理知识
及时复习
规范作业
训练思维
认真纠错
提升能力
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
