人教版八年级上册12.2三角形全等判定SSS 课件(21张)
文档属性
| 名称 | 人教版八年级上册12.2三角形全等判定SSS 课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 19:26:34 | ||
图片预览





文档简介
(共21张PPT)
:任队长
欢迎来到数学大讲堂
人教版
tan
.八年级上册
要
证
全
等
三
角
形
三
边
全
等
准
能
行
目录
新课导入
学习新知
知识捡漏
回顾旧知
布置作业
课堂总结
回顾旧知
①
形状和大小相同,能够完全重合的两个图形是全等形。
②
能够完全重合的三角形是全等三角形
①平移
②翻折(轴对称)
③旋转
①全等三角形的对应边相等
②全等三角形的对应角相等
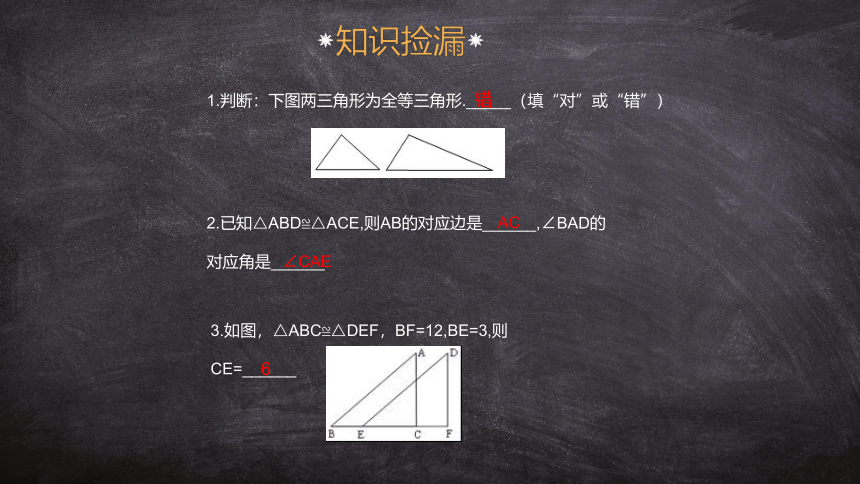
知识捡漏
2.已知△ABD≌△ACE,则AB的对应边是______,∠BAD的
对应角是______
1.判断:下图两三角形为全等三角形._____(填“对”或“错”)
3.如图,△ABC≌△DEF,BF=12,BE=3,则
CE=______
错
AC
∠CAE
6
12.2-1
全等三角形的判定“边边边”(SSS)
课前把控
新课导入
小明,我来考考你,工人师傅常用角尺平分一个任意角,你知道原理么?
这个么...?
情景导入:
刚上完全等三角形判定的小明,
放学后被数学老师叫住了...
学习新知
上一章节我们学习了两个能够完全重合的三角形是全等三角形,那么证明两个三角形全等必须得有三边对应相等,三个角对应相等六个条件么?
能不能用更少的条件就能证明两个三角形全等呢?
思考:
下面就让我们一探究竟吧!
学习新知
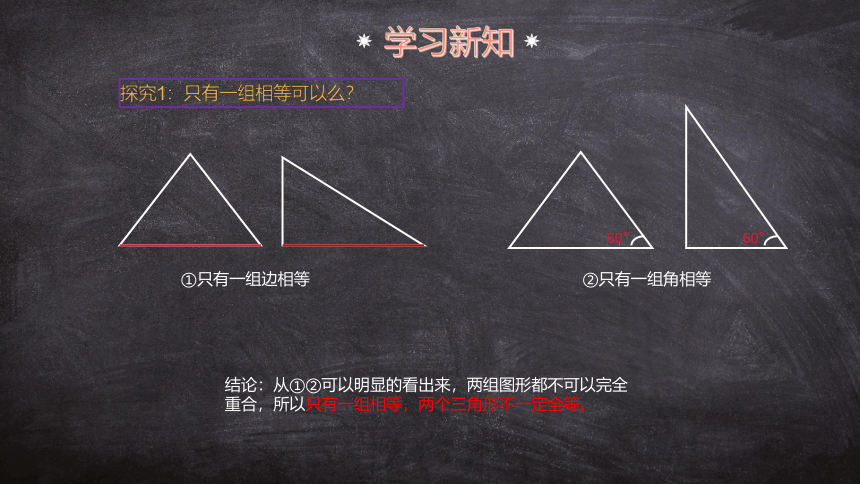
探究1:只有一组相等可以么?
①只有一组边相等
60°
60°
②只有一组角相等
结论:从①②可以明显的看出来,两组图形都不可以完全重合,所以只有一组相等,两个三角形不一定全等。
学习新知
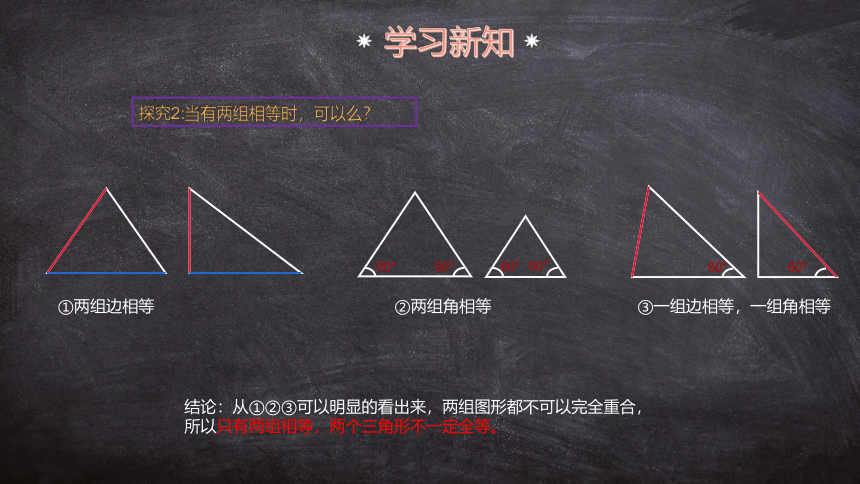
探究2:当有两组相等时,可以么?
①两组边相等
60°
60°
60°
60°
②两组角相等
60°
60°
③一组边相等,一组角相等
结论:从①②③可以明显的看出来,两组图形都不可以完全重合,
所以只有两组相等,两个三角形不一定全等。
学习新知
探究3:有三组相等时,可以么?
大三角形的内角都是60°,小三角形的内角也都是60°,也就是有三组角相等
结论:从图可以明显的看出来,两组图形都不可以完全重合,
所以只有三组角相等,两个三角形不一定全等。
学习新知
两个三组边分别对应相等的三角形全等么?
先任意画出一个△ABC,再画出一个△A′B′C′
,使A′B′=
AB
,B′C′
=BC,
A′
C′
=AC.把画好的△A′B′C′剪下,放到△ABC上,他们完全重合吗?
作法:
(1)画B′C′=BC;
(2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A';
(3)连接线段A'B',A'C
'.
动动脑:作图的结果反映了什么情况?你能用文字语言和符号语言说明吗?
A
B
C
A'
B'
C
'
章节精华
判定三角形全等的方法:边边边
文字语言:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
在△ABC和△
A′B′C′
中,
∴
△ABC
≌
△A′B′C′(SSS).
AB=A′B′
BC=B′C′
AC=A′
C′
几何语言:
A
B
C
A'
B'
C
'
学习新知
经典例题:
如图,有一个三角形钢架,AB
=AC
,AD
是连接点A
与BC
中点D
的支架.求证:(1)△ABD
≌△ACD
.(2)
AD⊥BC
学习新知
C
B
D
A
证明:(1)∵
D
是BC中点,
∴ BD
=DC.
在△ABD
与△ACD
中,
∴
△ABD
≌
△ACD
(
SSS
).
AB
=AC
(已知)
BD
=CD
(已证)
AD
=AD
(公共边)
(2)∵△ABD
≌
△ACD
∴∠ADB=∠ADC
又∵∠ADB+∠ADC=180°
∴∠ADB=∠ADC=90°
即
AD⊥BC
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
证全等的书写过程(五行式)
学习新知
学习新知
如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.为什么呢?
大家还记得课程前面老师和小明的对话么?我们不妨把问题转化成数学语言。
证明:在△COM和△CON中
CM=CN
OC=OC
OM=ON
∴△COM≌△CON(SSS)
∴∠AOC=∠BOC,
即OC即是∠AOB的平分线.
1.已知:如图
,AB=AE,AC=AD,BD=CE,
求证:△ABC≌△AED.
证明:∵BD=CE,
∴BD-CD=CE-CD
.
∴BC=ED
.
在△ABC和△ADE中,
AC=AD
AB=AE
BC=ED
∴△ABC≌△AED(SSS).
巩固练习
=
=
×
×
2.已知:如图
,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE;
(2)
AC∥EF.
证明:(1)∵
AD=FB,
∴AB=FD(等式性质).
在△ABC和△FDE
中,
AC=FE(已知),
BC=DE(已知),
AB=FD(已证),
∴△ABC≌△FDE(SSS);
A
C
E
D
B
F
=
=
。
。
(2)∵
△ABC≌△FDE(已证).
∴
∠A=∠F(全等三角形的对应角相等).
∴AC∥EF
(内错角相等,两直线平行)
3.如图,AD=BC,AC=BD.求证:∠C=∠D
.(提示:
连结AB)
证明:连结AB两点
∴△ABD≌△BAC(SSS)
AD=BC,
BD=AC,
AB=BA,
在△ABD和△BAC中,
∴∠D=∠C.
课堂总结
本节课我们学习了哪些内容,你有什么样的收获、体会和困惑?
课后作业
完成钉钉上老师布置的作业!
谢谢聆听
:任队长
欢迎来到数学大讲堂
人教版
tan
.八年级上册
要
证
全
等
三
角
形
三
边
全
等
准
能
行
目录
新课导入
学习新知
知识捡漏
回顾旧知
布置作业
课堂总结
回顾旧知
①
形状和大小相同,能够完全重合的两个图形是全等形。
②
能够完全重合的三角形是全等三角形
①平移
②翻折(轴对称)
③旋转
①全等三角形的对应边相等
②全等三角形的对应角相等
知识捡漏
2.已知△ABD≌△ACE,则AB的对应边是______,∠BAD的
对应角是______
1.判断:下图两三角形为全等三角形._____(填“对”或“错”)
3.如图,△ABC≌△DEF,BF=12,BE=3,则
CE=______
错
AC
∠CAE
6
12.2-1
全等三角形的判定“边边边”(SSS)
课前把控
新课导入
小明,我来考考你,工人师傅常用角尺平分一个任意角,你知道原理么?
这个么...?
情景导入:
刚上完全等三角形判定的小明,
放学后被数学老师叫住了...
学习新知
上一章节我们学习了两个能够完全重合的三角形是全等三角形,那么证明两个三角形全等必须得有三边对应相等,三个角对应相等六个条件么?
能不能用更少的条件就能证明两个三角形全等呢?
思考:
下面就让我们一探究竟吧!
学习新知
探究1:只有一组相等可以么?
①只有一组边相等
60°
60°
②只有一组角相等
结论:从①②可以明显的看出来,两组图形都不可以完全重合,所以只有一组相等,两个三角形不一定全等。
学习新知
探究2:当有两组相等时,可以么?
①两组边相等
60°
60°
60°
60°
②两组角相等
60°
60°
③一组边相等,一组角相等
结论:从①②③可以明显的看出来,两组图形都不可以完全重合,
所以只有两组相等,两个三角形不一定全等。
学习新知
探究3:有三组相等时,可以么?
大三角形的内角都是60°,小三角形的内角也都是60°,也就是有三组角相等
结论:从图可以明显的看出来,两组图形都不可以完全重合,
所以只有三组角相等,两个三角形不一定全等。
学习新知
两个三组边分别对应相等的三角形全等么?
先任意画出一个△ABC,再画出一个△A′B′C′
,使A′B′=
AB
,B′C′
=BC,
A′
C′
=AC.把画好的△A′B′C′剪下,放到△ABC上,他们完全重合吗?
作法:
(1)画B′C′=BC;
(2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A';
(3)连接线段A'B',A'C
'.
动动脑:作图的结果反映了什么情况?你能用文字语言和符号语言说明吗?
A
B
C
A'
B'
C
'
章节精华
判定三角形全等的方法:边边边
文字语言:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
在△ABC和△
A′B′C′
中,
∴
△ABC
≌
△A′B′C′(SSS).
AB=A′B′
BC=B′C′
AC=A′
C′
几何语言:
A
B
C
A'
B'
C
'
学习新知
经典例题:
如图,有一个三角形钢架,AB
=AC
,AD
是连接点A
与BC
中点D
的支架.求证:(1)△ABD
≌△ACD
.(2)
AD⊥BC
学习新知
C
B
D
A
证明:(1)∵
D
是BC中点,
∴ BD
=DC.
在△ABD
与△ACD
中,
∴
△ABD
≌
△ACD
(
SSS
).
AB
=AC
(已知)
BD
=CD
(已证)
AD
=AD
(公共边)
(2)∵△ABD
≌
△ACD
∴∠ADB=∠ADC
又∵∠ADB+∠ADC=180°
∴∠ADB=∠ADC=90°
即
AD⊥BC
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
证全等的书写过程(五行式)
学习新知
学习新知
如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.为什么呢?
大家还记得课程前面老师和小明的对话么?我们不妨把问题转化成数学语言。
证明:在△COM和△CON中
CM=CN
OC=OC
OM=ON
∴△COM≌△CON(SSS)
∴∠AOC=∠BOC,
即OC即是∠AOB的平分线.
1.已知:如图
,AB=AE,AC=AD,BD=CE,
求证:△ABC≌△AED.
证明:∵BD=CE,
∴BD-CD=CE-CD
.
∴BC=ED
.
在△ABC和△ADE中,
AC=AD
AB=AE
BC=ED
∴△ABC≌△AED(SSS).
巩固练习
=
=
×
×
2.已知:如图
,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE;
(2)
AC∥EF.
证明:(1)∵
AD=FB,
∴AB=FD(等式性质).
在△ABC和△FDE
中,
AC=FE(已知),
BC=DE(已知),
AB=FD(已证),
∴△ABC≌△FDE(SSS);
A
C
E
D
B
F
=
=
。
。
(2)∵
△ABC≌△FDE(已证).
∴
∠A=∠F(全等三角形的对应角相等).
∴AC∥EF
(内错角相等,两直线平行)
3.如图,AD=BC,AC=BD.求证:∠C=∠D
.(提示:
连结AB)
证明:连结AB两点
∴△ABD≌△BAC(SSS)
AD=BC,
BD=AC,
AB=BA,
在△ABD和△BAC中,
∴∠D=∠C.
课堂总结
本节课我们学习了哪些内容,你有什么样的收获、体会和困惑?
课后作业
完成钉钉上老师布置的作业!
谢谢聆听
