题型分类教案:三棱锥外接球问题(高三复习)
文档属性
| 名称 | 题型分类教案:三棱锥外接球问题(高三复习) | 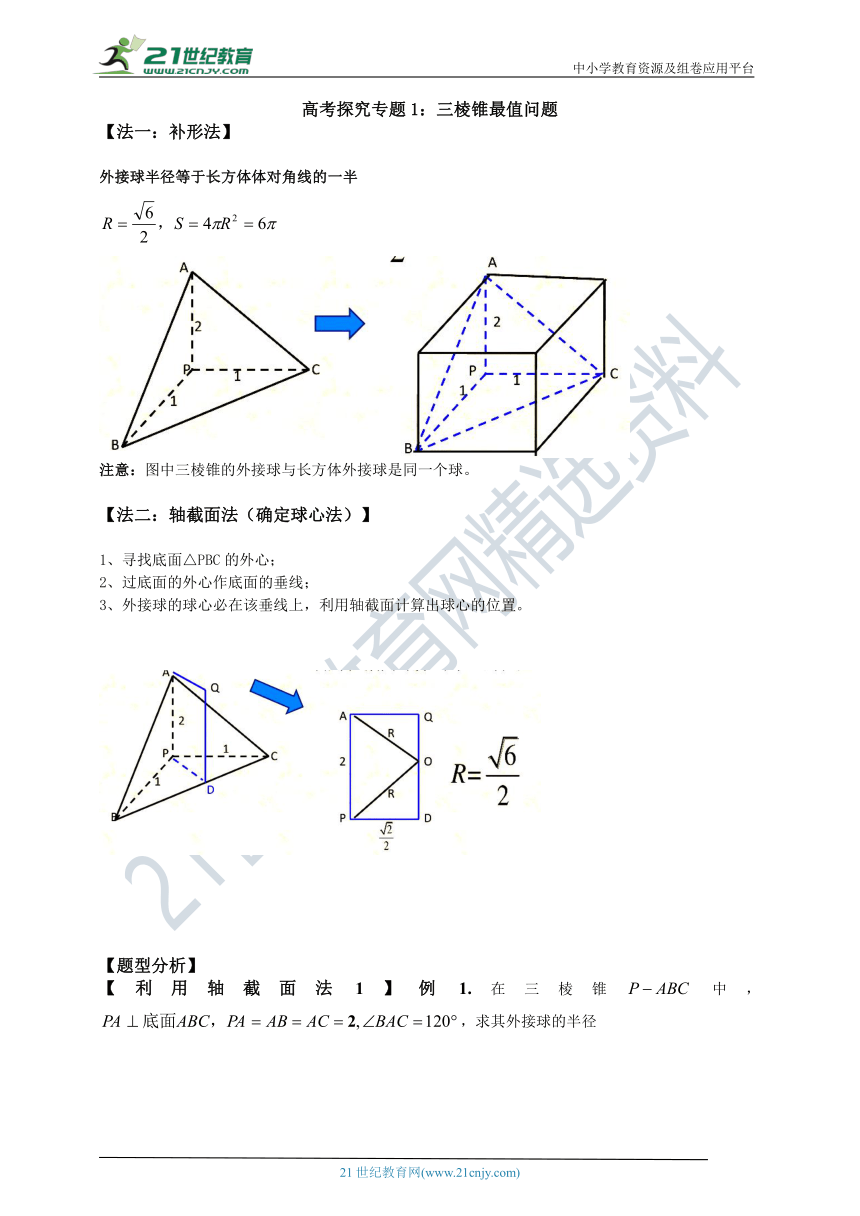 | |
| 格式 | doc | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 16:21:08 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
高考探究专题1:三棱锥最值问题
【法一:补形法】
外接球半径等于长方体体对角线的一半
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法(确定球心法)】
1、寻找底面△PBC的外心;
2、过底面的外心作底面的垂线;
3、外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【题型分析】
【利用轴截面法1】例1.在三棱锥中,,求其外接球的半径
【变式1】已知在三棱锥,,求该三棱锥外接球的表面积与体积。
【变式2】在四面体中,平面,,,,则该四面体的外接球的表面积为
【变式3】三棱锥中,平面,则该三棱锥外接球的表面积为( ) A. B. C. D.
【变式4】如图,已知点A、B、C、D是球的球面上四点,DA平面ABC,ABBC,DA=AB=BC=,则球的表面积等于_________.
【利用轴截面法2】例2.三棱锥P-ABC内接于半径为2的球中,PA⊥平面ABC,∠BAC=90°,BC=2,则三棱锥P-ABC的体积最大值是
【变式1】三棱锥P-ABC内接于半径为4的球中,PA⊥平面ABC,∠BAC=45°,BC=2,则三棱锥P-ABC的体积最大值是
【变式2】已知球的直径,、是该球球面上的两点,,则棱锥的体积最大为( ) A.2 B. C. D.
【答案】A
【解析】如图所示,∵线段是球的直径且,,
∴,,,,,
(其中为点到底面的距离),故当最大时,的体积最大,由图可得当面面时,最大且满足,即,
此时,故选A.
【变式3】在三棱锥中,,则三棱锥外接球的体积的最小值为( )
A. B. C. D.
【利用图形的特殊性】
例3.已知在三棱锥,,求该三棱锥外接球的表面积与体积。
【变式1】已知三棱锥的各条棱长均为1,求其外接球的表面积。
【变式2】在四面体ABCD中,,求其外接球的表面积
例4.在矩形中,,沿将矩形折成一个直二面角,则四面体的外接球的体积为( )
A. B. C. D.
解:设矩形对角线的交点为,则由矩形对角线互相平分,可知.∴点到四面体的四个顶点的距离相等,即点为四面体的外接球的球心,如图2所示.∴外接球的半径.故.选C.
【变式】已知边长为1的正方形,沿对角线把折起,则三棱锥的外接球的表面积等于_______.
答案:;
【解析】三棱锥的外接球的球心为AC中点,即AC为球直径,因此外接球的表面积等于
例5.已知三棱锥P-ABC中,PA=PB=2PC=2,是边长为的正三角形,则三棱锥P-ABC的外接球半径为_________.
答案:;
【解析】由题意可得PC⊥平面ABC,以PC为一条侧棱,△ABC为底面把三棱锥
P-ABC补成一个直三棱柱,则该直三棱柱的外接球就是三棱锥P-ABC的外接球,且该直三棱柱上、下底面的外接圆圆心连线的中点就是球心,因为底面外接圆的半r=1,所以三棱锥P-ABC的外接球半径.
【变式】三棱锥中,且,是边长为的等边三角形,则该三棱锥外接球的表面积为( ) A. B. C. D.
【综合提升练习】
1.已知如图所示的三棱锥的四个顶点均在球的球面上,和所在的平面互相垂直,,,,则球的表面积为( ? )
A. B. C. D.
解析:如图所示,∵,∴为直角,即过的小圆面的圆心为的中点,和所在的平面互相垂直,则圆心在过的圆面上,即的外接圆为球的大圆,由等边三角形的重心和外心重合易得球半径,球的表面积为,故选.
2.已知是球的球面上两点,,为该球面上的动点,若三棱锥体积的最大值为,则球的表面积为( )
A. B. C. D.
解析
如图所示,当点位于垂直于面的直径端点时,三棱锥的体积最大,
设球的半径为,此时,
故,则球的表面积为,故选.
3.如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )
A. B. C. D.
解析
该几何体为三棱锥,设球心为,
分别为和的外心,
易求得,,
∴球的半径,
∴该几何体外接球的表面积为.
4.一个三条侧棱两两互相垂直并且侧棱长都为的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( ? )
A. B. C. D.
解析
由题可知该三棱锥为一个棱长的正方体的一角,则该三棱锥与该正方体有相同的外接球,又正方体的对角线长为,则球半径为,则. 故选.
5.若三棱锥的三个侧面两两垂直,且侧棱长均为,则其外接球的表面积是.
【答案】
【解析】,.
6.已知三棱锥的四个顶点均在同一个球面上,底面满足,,若该三棱锥体积的最大值为3,则其外接球的体积为( )
A. B. C. D.
【答案】D
【解析】因为是等腰直角三角形,所以外接球的半径是,设外接球的半径是,球心到该底面的距离,如图,则,,由题设,
最大体积对应的高为,故,即,解之得,
所以外接球的体积是,故答案为D.
7.把边长为3的正方形沿对角线对折,使得平面平面,则三棱锥的外接球的表面积为()
A. B. C. D.
【答案】C
【解析】把边长为3的正方形沿对角线对折,使得平面平面,
则三棱锥的外接球直径为,外接球的表面积为,故选C
8.三棱锥的所有顶点都在球的表面上,平面,,,则球的表面积为()
A. B. C. D.
【答案】D【解析】因为,,所以,,
因此三角形外接圆半径为,
设外接球半径为,则,,故选D
9.已知球的半径为,,,三点在球的球面上,球心到平面的距离为,,,则球的表面积为()
A. B. C. D.
【答案】D
【解析】由余弦定理得:,
设三角外接圆半径为,由正弦定理可得:,则,
又,解得:,则球的表面积.本题选择D选项.
10.已知正四棱锥(底面四边形是正方形,顶点在底面的射影是底面的中心)的各顶点都在同一球面上,底面正方形的边长为,若该正四棱锥的体积为,则此球的体积为( )
A. B. C. D.
【答案】C
【解析】
如图,设正方形的中点为,正四棱锥的外接球心为,
底面正方形的边长为,,
正四棱锥的体积为,,
则,,
在中由勾股定理可得:,解得,,故选C.
11.四面体中,,,,则此四面体外接球的表面积为()
A. B. C. D.
【答案】A
【解析】
由题意,中,,,可知是等边三角形,,
∴的外接圆半径,,
∵,可得,可得,∴,∴,
∴四面体高为.
设外接球,为球心,,可得:……①,
……②
由①②解得:.四面体外接球的表面积:.故选A.
_21?????????è?????(www.21cnjy.com)_
高考探究专题1:三棱锥最值问题
【法一:补形法】
外接球半径等于长方体体对角线的一半
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法(确定球心法)】
1、寻找底面△PBC的外心;
2、过底面的外心作底面的垂线;
3、外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【题型分析】
【利用轴截面法1】例1.在三棱锥中,,求其外接球的半径
【变式1】已知在三棱锥,,求该三棱锥外接球的表面积与体积。
【变式2】在四面体中,平面,,,,则该四面体的外接球的表面积为
【变式3】三棱锥中,平面,则该三棱锥外接球的表面积为( ) A. B. C. D.
【变式4】如图,已知点A、B、C、D是球的球面上四点,DA平面ABC,ABBC,DA=AB=BC=,则球的表面积等于_________.
【利用轴截面法2】例2.三棱锥P-ABC内接于半径为2的球中,PA⊥平面ABC,∠BAC=90°,BC=2,则三棱锥P-ABC的体积最大值是
【变式1】三棱锥P-ABC内接于半径为4的球中,PA⊥平面ABC,∠BAC=45°,BC=2,则三棱锥P-ABC的体积最大值是
【变式2】已知球的直径,、是该球球面上的两点,,则棱锥的体积最大为( ) A.2 B. C. D.
【答案】A
【解析】如图所示,∵线段是球的直径且,,
∴,,,,,
(其中为点到底面的距离),故当最大时,的体积最大,由图可得当面面时,最大且满足,即,
此时,故选A.
【变式3】在三棱锥中,,则三棱锥外接球的体积的最小值为( )
A. B. C. D.
【利用图形的特殊性】
例3.已知在三棱锥,,求该三棱锥外接球的表面积与体积。
【变式1】已知三棱锥的各条棱长均为1,求其外接球的表面积。
【变式2】在四面体ABCD中,,求其外接球的表面积
例4.在矩形中,,沿将矩形折成一个直二面角,则四面体的外接球的体积为( )
A. B. C. D.
解:设矩形对角线的交点为,则由矩形对角线互相平分,可知.∴点到四面体的四个顶点的距离相等,即点为四面体的外接球的球心,如图2所示.∴外接球的半径.故.选C.
【变式】已知边长为1的正方形,沿对角线把折起,则三棱锥的外接球的表面积等于_______.
答案:;
【解析】三棱锥的外接球的球心为AC中点,即AC为球直径,因此外接球的表面积等于
例5.已知三棱锥P-ABC中,PA=PB=2PC=2,是边长为的正三角形,则三棱锥P-ABC的外接球半径为_________.
答案:;
【解析】由题意可得PC⊥平面ABC,以PC为一条侧棱,△ABC为底面把三棱锥
P-ABC补成一个直三棱柱,则该直三棱柱的外接球就是三棱锥P-ABC的外接球,且该直三棱柱上、下底面的外接圆圆心连线的中点就是球心,因为底面外接圆的半r=1,所以三棱锥P-ABC的外接球半径.
【变式】三棱锥中,且,是边长为的等边三角形,则该三棱锥外接球的表面积为( ) A. B. C. D.
【综合提升练习】
1.已知如图所示的三棱锥的四个顶点均在球的球面上,和所在的平面互相垂直,,,,则球的表面积为( ? )
A. B. C. D.
解析:如图所示,∵,∴为直角,即过的小圆面的圆心为的中点,和所在的平面互相垂直,则圆心在过的圆面上,即的外接圆为球的大圆,由等边三角形的重心和外心重合易得球半径,球的表面积为,故选.
2.已知是球的球面上两点,,为该球面上的动点,若三棱锥体积的最大值为,则球的表面积为( )
A. B. C. D.
解析
如图所示,当点位于垂直于面的直径端点时,三棱锥的体积最大,
设球的半径为,此时,
故,则球的表面积为,故选.
3.如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )
A. B. C. D.
解析
该几何体为三棱锥,设球心为,
分别为和的外心,
易求得,,
∴球的半径,
∴该几何体外接球的表面积为.
4.一个三条侧棱两两互相垂直并且侧棱长都为的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( ? )
A. B. C. D.
解析
由题可知该三棱锥为一个棱长的正方体的一角,则该三棱锥与该正方体有相同的外接球,又正方体的对角线长为,则球半径为,则. 故选.
5.若三棱锥的三个侧面两两垂直,且侧棱长均为,则其外接球的表面积是.
【答案】
【解析】,.
6.已知三棱锥的四个顶点均在同一个球面上,底面满足,,若该三棱锥体积的最大值为3,则其外接球的体积为( )
A. B. C. D.
【答案】D
【解析】因为是等腰直角三角形,所以外接球的半径是,设外接球的半径是,球心到该底面的距离,如图,则,,由题设,
最大体积对应的高为,故,即,解之得,
所以外接球的体积是,故答案为D.
7.把边长为3的正方形沿对角线对折,使得平面平面,则三棱锥的外接球的表面积为()
A. B. C. D.
【答案】C
【解析】把边长为3的正方形沿对角线对折,使得平面平面,
则三棱锥的外接球直径为,外接球的表面积为,故选C
8.三棱锥的所有顶点都在球的表面上,平面,,,则球的表面积为()
A. B. C. D.
【答案】D【解析】因为,,所以,,
因此三角形外接圆半径为,
设外接球半径为,则,,故选D
9.已知球的半径为,,,三点在球的球面上,球心到平面的距离为,,,则球的表面积为()
A. B. C. D.
【答案】D
【解析】由余弦定理得:,
设三角外接圆半径为,由正弦定理可得:,则,
又,解得:,则球的表面积.本题选择D选项.
10.已知正四棱锥(底面四边形是正方形,顶点在底面的射影是底面的中心)的各顶点都在同一球面上,底面正方形的边长为,若该正四棱锥的体积为,则此球的体积为( )
A. B. C. D.
【答案】C
【解析】
如图,设正方形的中点为,正四棱锥的外接球心为,
底面正方形的边长为,,
正四棱锥的体积为,,
则,,
在中由勾股定理可得:,解得,,故选C.
11.四面体中,,,,则此四面体外接球的表面积为()
A. B. C. D.
【答案】A
【解析】
由题意,中,,,可知是等边三角形,,
∴的外接圆半径,,
∵,可得,可得,∴,∴,
∴四面体高为.
设外接球,为球心,,可得:……①,
……②
由①②解得:.四面体外接球的表面积:.故选A.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
