高中物理教科版必修1_4. 速度变化快慢的描述——加速度课件58张PPT
文档属性
| 名称 | 高中物理教科版必修1_4. 速度变化快慢的描述——加速度课件58张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览










文档简介
1.5 速度变化快慢的描-加速度
思考与讨论
普通的小型轿车和旅客列车,速度都能达到100 km/h。但是,它们起步后达到这样的速度所需的时间是不一样的。例如一辆小汽车在20 s内速度达到了100 km/h,而一列火车达到这个速度大约要用500 s。
谁的速度“增加”得比较快?它们的速度平均1 s各增加多少?
小汽车的速度“增加”得比较快!
20 s
速度0
100km/h(约28m/s)
速度平均1 s 增加为
500 s
速度0
100km/h(约28m/s)
速度平均1 s 增加为
羚羊
猎豹
4 s
速度0
25m/s
速度平均1 s 增加为
4 s
速度0
30m/s
速度平均1 s 增加为
猎豹的速度“增加”得比较快!
炮弹的速度变化,比飞机的速度变化快得多!
30 s
速度0
300km/h(约83m/s)
速度平均1 s 增加为
0.005 s
速度0
250m/s
速度平均1 s 增加为
v1/m.s-1
△t/s
v2/m.s-1
△v/m·s-1
A. 自行车下坡
2
3
11
B. 公共汽车出站
0
3
6
C. 某舰艇出航
0
20
6
D. 火车出站
0
100
20
E. 飞机匀速飞行
300
10
300
9
6
0
6
20
谁的速度大?
谁的速度变化得快?
再举出一些例子,说明“速度大”、“速度变化大”、“速度变化得快”描述的是三种不同的情况。
谁的速度的变化量大?
v1/(m·s-1)
△t/s
v2/(m·s-1)
△v/ (m·s-1)
A.自行车下坡
2
3
11
B.公共汽车出站
0
3
6
C.某舰艇出航
0
20
6
D.火车出站
0
100
20
E.飞机匀速飞行
300
10
300
9
6
0
6
20
△v/△t(m·s-2)
3
2
0.3
0.2
0
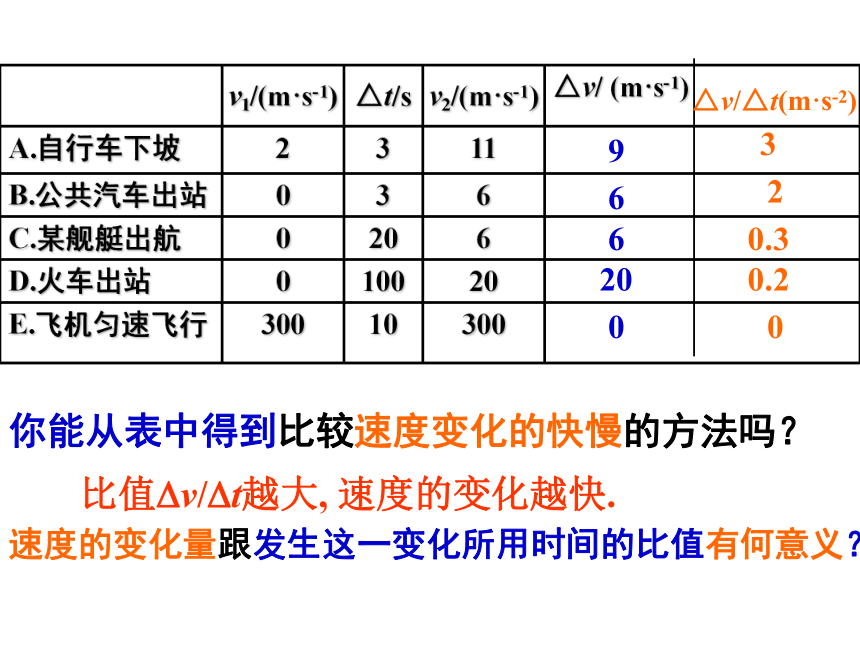
你能从表中得到比较速度变化的快慢的方法吗?
速度的变化量跟发生这一变化所用时间的比值有何意义?
比值?v/?t越大, 速度的变化越快.
“速度大”、“速度变化大”、“速度变化得快”描述的是三种不同的情况。
“速度大”,是指位置变化快 。
“速度变化大”,是指末速度与初速度的差别大。
“速度变化得快” ,是指单位时间内速度变化大。
一、加速度
⒈ 定义:
v1----初速度(时间△t开始时的速度)
v2----末速度(时间△t末了时的速度)
⒉ 定义式:
a ----加速度(时间△t范围内的加速度)
⒊ 物理意义:描述速度变化快慢的物理量
速度的变化量跟发生这一变化所用时间的比值。
4、单位:国际单位—米/秒2 符号m/s2 读法:米每二次方秒
5、加速度是矢量,方向与速度变化量△v的方向相同
汽车的加速性能(制动距离)是反映汽车性能的重要指标.下列哪种汽车的加速性能最优越?
0~100km/h加速时间:
夏利15s
宝来10.5s
奔驰6.5s
宝马5.6s
F-1赛车2.3s.
一些运动物体的加速度
一些运动物体的加速度
速度很大,加速度很小
加速度很大,速度不太大
二、加速度方向与速度方向的关系(直线运动)
⒈ 速度的变化量△v
⑴ 定义: 末速度减去初速度
⑵ 定义式 △v = v2-v1
⑶ 作图法寻找 △v
Δ
v
v1
v2
Δ
v
v1
v2
① 加速直线运动
②减速直线运动
a
a
在直线运动中, a ,v共线
②图解法:以初速度的箭头为起点,以末速度的箭头为终点,做出一个新的有向线段,它就表示速度的变化量△V。
这个计算法则对速度不在一条直线上也是正确的。
速度的变化量是矢量。
V2
V1
△V
V1
V2
△V
如图所示,求小球在碰撞过程中,速度的变化量?
3m/s
3m/s
正方向
1. 规定某一方向(一般以初速度方向)为正方向
2.表示已知量:已知量与规定正方向相同,计为正;相反,记为负
速度的变化量等于末速度减初速度,
即Δv=v2-v1 =-3m/s-3m/s=-6m/s,
v1 =3m/s,
v2=-3m/s,
3.求解的结果:矢量的正负只表示方向(与规定正方向同向还是反向),不表示大小
一条直线上运动问题的解决方法:
二、加速度方向与速度方向的关系(直线运动)
⒉ 加速度 (a = △v/△t )的方向
在变速直线运动中,若以初速度v1方向为正方向,
① 加速直线运动,a ___0,a的方向 ;
② 减速直线运动,a ___0, a的方向 。
结论:加速度方向和速度变化量△v的方向相同,与速度方向无关。
>
与v1方向相同
<
与v1方向相反
⒈ 速度的变化量△v
理解加速度的概念
物体做直线运动,初速度为v1,经过时间?t=1s,速度变为v2。分别求出下述情况的加速度。
1.v1=2m/s,向右, v2=5m/s;
2.v1=5m/s,向右, v2=2m/s;
3.v1=2m/s,向右, v2=-2m/s;
注意矢量性,要回答方向!!
以初速度方向为正方向:
三、加速度大小与速度大小的关系
⒈ 速度大,加速度不一定大;
⒉ 加速度为零时,速度可以不为零;
结论:加速度与速度没有必然联系。
加速度大,速度不一定大。
速度为零时,加速度可以不为零。
速度变化量大,加速度不一定大;
结论:加速度与速度变化量大小没有必然联系。
四、加速度大小与速度变化量大小的关系
加速度大,速度变化量不一定大。
瞬时速度
瞬时加速度
取很小很小的值 0
取很小很小的值 0
五、平均加速度和瞬时加速度
1、平均加速度:粗略描述速度变化快慢
公式: a=? v / ? t
2、瞬时加速度:精确描述每一时刻速度变化快慢
3、匀变速运动:加速度不变的沿着一条直线的运动。
匀变速运动中,平均加速度与瞬时加速度相等。
六、变化率
⒈ 定义:
⒉ 物理意义:
某量D的变化量△D与发生这个变化所用的时间△t 的比值△D/△t ,叫做这个量的变化率。
描述某量D的变化快慢,不表示某量D的变化量△D的大小。
快慢
速度
变化
加速度
速度
快慢
位置
变化
速度描述物体位置变化的快慢,即位置的变化率;
△ x
v = ——
△t
位置
速度
变化的快慢
变化的快慢
加速度
△ v
a = ——
△t
加速度描述速度变化的快慢,即速度的变化率。
速度V
速度变化量ΔV
加速度a
定义式
Δv= v-v0
意义
表物体运动(位置变化)的快慢
表速度的变化
表示速度变化的快慢
a大,速度变化快
单位
m/s
m/s
m/s2
方向
质点运动的方向即运动轨迹的切线方向
由Δv= v-v0决定的方向,可能与v0方向相同也可能与v0方向相反
与速度的变化Δv方向相同,而与速度方向无关
大小
1 位移与时间的比值
2位置对时间的变化率
3X-t坐标系中曲线的斜率大小
Δv= v-v0
1速度变化量与时间的比值
2 速度对时间的变化率
3 v-t坐标系中曲线的斜率大小
与时间的关系
与时刻对应
状态量
与时间间隔对应
过程量
瞬时加速度对应时刻平均加速度对应时间
联系
⑴、 a的大小、方向与速度的大小、方向没有直接的关系。(2) a的大小与Δv的大小没有直接的关系。但是a的方向与Δv的方向总是相同的。(3)有了a,速度一定要变化,物体是加速、减速不是由加速度的正负决定,而是由a与v的关系定: a与v同向,加速;a与v反向,减速
比较位置X、位移△X、速度V的关系
?
位置X
位移△X
速度V
定义式
X=?
△X=X2-X1
△X/△t
意义
表示物体的位置
表示位置改变
表示位置改变的快慢
大小
用坐标表示
坐标的差
运动快慢,表示位置变化的快慢,位置变化率
方向
从初位置指向末位置
与位移△X同向
单位
m
m
m/s
与时间的关系
与时刻对应
状态量
与时间间隔对应
过程量
平均速度对应时间
瞬时速度对应时刻
1、若vt>v0,则△v ____0,
物体做_______运动;
2、若vt 物体做_______运动。
练习:在直线运动中
表达式: △v = vt-v0
3、 加速度 (a = △v/ △t )
以速度方向为正,① 加速运动,a ___ 0
② 减速运动,a ___ 0
4、加速度是____量
① 加速运动,a的方向____________
② 减速运动,a的方向____________
5、匀变速直线运动:是_____不变的运动。
a、b分别是两个物体运动的v-t图像。哪个物体运动的加速度较大?为什么?
七、从v-t 图象看加速度
?t
?v
t1
v1
t2
v2
b
v(m/s)
O
a
从曲线的倾斜程度就能判断加速度的大小,
比值?v/?t就是加速度的数值。
小三角形水平的直角边代表时间间隔?t,竖直直角边代表速度的变化量?v 。
t/s
⒈ 从v-t图象的—————— 看加速度的大小;
⒉ 由v-t图像计算加速度的大小。
六、从v-t 图象看加速度
倾斜程度(斜率)
t/s
O
v/m·s-1
10
15
5
4
6
2
A
B
思考:A、B两物体的速度哪个变化快?
A物体的加速度为 ;
B物体的加速度为 。
0.5m/s2
0.2m/s2
v-t 图像的斜率就是加速度
七、从v-t 图象看加速度
减速运动的v-t图像应该怎样画呢?
课堂小结:
速度的改变
速度
加速度
表示运动的快慢
表示速度的变化
表示速度变化的快慢
v
Δv=vt-v0
1、定义:速度的改变跟发生这一改变所用的时间的比值
2、公式:
4、矢量性:加速度的方向与速度变化的方向相同
5、匀变速直线运动的特点:加速度是恒定的
3、单位:m/s
2
⑴速度大,加速度不一定大;
加速度大, 速度不一定大。
⑵加速度为零,速度不一定为零;
速度为零,加速度也不一定为零
2、加速度和速度的区别
①它们的含义不同
速度描述的是位置变化的快慢
加速度描述的是速度变化的快慢
②看它们的大小情况
加速度大小和速度大小没必然联系;但 若a不为零,V一定变化
加速度 a = ( vt - v0 ) / △t
某一物理量的变化跟发生这一变化所用的时间的比值,叫做该量对时间的变化率。加速度是速度对时间的 变化率
3、加速度和速度的变化量(Δv = vt - vo):
速度的变化量表示速度改变了多少。等于物体末速度和初速度的矢量差(也为 矢量).
所以:速度变化量大,加速度不一定大;
a 与Δv 也无直接联系
加速度就是增加的速度吗?
加速度只能针对加速运动而言吗? 对减速运动适合吗?
如何表示减速运动的加速度呢?
思考与讨论
1)速度大,加速度也一定大吗?
3)速度变化量大,加速度也一定大吗?
2)加速度大,速度也一定大吗?
速度大,加速度不一定大;加速度大,速度不一定大.
速度变化量大,加速度不一定大.
思考与讨论
4)加速度为零时,速度也一定为零吗?
5)速度为零时,加速度也一定为零吗?
加速度为零,速度可以不为零;
速度为零,加速度可以不为零.
①加速度方向和初速度方向相同
速度增加
加速运动
②加速度方向和初速度方向相反
速度减小
减速运动
6)加速度增加的运动是加速运动,加速度减小的运动是减速运动.这种认识对吗?
(如果不对,你认为应该怎样根据加速度判断物体的速度是增加还是减小?)
判断下列说法是否正确,并举例说明:
①速度大,加速度不一定大;
②加速度大,速度不一定大;
③速度变化量大,加速度不一定大;
④加速度为零,速度不一定为零;
⑤速度为零,加速度可以不为零。
说明:加速度是速度的变化率,与速度大小无直接关系。
如:匀速
如:启动
如:t大
如:匀速
如:启动
⑴ 飞机起飞前在地面上滑行,可以在30s内,速度由零增加到81m/s。那么,飞机起飞前的加速度为多少?
⑵汽车急刹车时,可以在3秒内速度由18m/s减小到零。那么,汽车急刹车时的加速度为多少?
加速度的正、负的含义是什么呢?
以初速度方向为正方向:
O
v/m·s-1
t/s
4
6
2
4
6
2
1、前2s内的加速度为
2、2s—4s的加速度为
0
3、4s—6s的加速度为
注意:加速度为负值表示速度减小,此时,加速度方向与速度方向相反
D
⒈ 下列说法正确的是 ( )
A. 物体速度改变量大,其加速度一定大
B. 物体有加速度时,速度就增大
C. 物体的加速度大,速度一定大
D. 物体速度的变化率大,加速度一定大
⒉ 关于加速度的含义,下列说法正确的是( )
A. 加速度表示速度的增加
B. 加速度表示速度变化
C. 加速度表示速度变化快慢
D. 加速度表示速度变化的大小
C
⒊ 下列说法正确的是:
A. 加速度增大,速度一定增大( )
B. 速度变化越大,加速度越大
C. 物体有加速度,速度就增大
D. 物体的速度很大,加速度可能为零
D
⒋ 以下关于加速度的说法中,正确的是( )
A. 加速度为0的物体一定处于静止状态
B. 物体的加速度减小,其速度必随之减小
C. 物体的加速度增加,其速度不一定增大
D. 物体的加速度越大,其速度变化越快
CD
⒌ 关于速度、速度改变量、加速度,正确的说法是:
A、物体运动的速度改变量很大,它的加速度一定 很大
B、速度很大的物体,其加速度可以很小,可以为零
C、某时刻物体的速度为零,其加速度不可能为零
D、加速度很大时,运动物体的速度一定很大
B
C
⒍ 一个物体的加速度为零,则该物体一定是 ( )
A. 静止不动
B. 匀速直线运动
C. 静止或匀速直线运动
D. 做速度大小不变的运动
D
⒎ 下列关于速度和加速度的叙述中,结论正确的是
A. 物体的速度越大,它的加速度也一定越大
B. 物体运动的加速度为零,它的速度也为零
C. 物体运动的速度改变越大,它的加速度也一定越大
D. 加速度的大小就是速度对时间的变化率的大小
BD
⒏ 若汽车的加速度方向与速度方向一致,当加速度减小时,则 ( )
A.汽车的速度也减小
B.汽车的速度仍在增大
C.当加速度减小到零时,汽车静止
D. 当加速度减小到零时,汽车的速度达到最大
10. 甲乙两物体的速度图象如图所示,由图可知a甲= ,a乙= ;t = 时,v甲= v乙;若
t = 时甲追上乙,再过1s乙在甲 (填前、后)方。
v/m.s-1
t/s
o
8
4
4
8
甲
乙
0
-1m/s-2
4s
8s
后
专题:
V-t图象中的加速度
1、V-t图象上的各个“点”表示什么意义?
关于v-t图象的物理意义:
t1
v1
t2
v2
表示:某时刻物体的速度
2、v-t图象上的“线”反映什么?
表示:速度随时间变化的规律
根据v-t图象判断物体的运动情况:
0
t
v
(B)
x
o
以v0速度做匀速直线
x
o
初速度为零的加速直线
0
t
v
(A)
v0
0
t
v
(C)
v0
0
t
v
(D)
v0
x
o
以初速度v0做加速直线
x
o
以初速度v0做减速直线
0
t
v
(E)
t0
-2
2
-1
1
t2
t1
0
t
v
(F)
2
-2
t0
t1
x
o
x
o
正方向减速
-2
0
负向减速
正方向加速
2
0
负方向加速
根据v-t图象求物体的加速度:
v/m.s-1
t/s
0
1
t1
t2
v1
v2
v0
?v1
?t1
思考1:能根据v-t图象求物体t1~t2和t0~t2时间内的加速度吗?如何求?
思考2:你认为此物体在0~t1内的加速度和t1~t2的加速度有什么关系?为什么?
?v2
?t2
思考3:你能根据v-t图象定性判断物体加速度的大小吗?怎么判断?
2
a2>a1
结论:
根据v-t图象求物体的加速度:
v/m.s-1
t/s
0
1
t1
t2
v1
v2
v0
2
a2>a1
2、加速度不变的运动叫匀变速运动;匀变速直线运动的v-t图象是一条倾斜的直线。
1、可以根据图线的倾斜程度来定性判断变速运动加速度的大小。
3
3、匀变速直线运动包括匀加速和匀减速直线运动。
a2>a3>a1
练习:某物体的运动v-t图象如下,问:
v/m.s-1
t/s
0
2
4
10
14
6
8
1、物体在各个时间段内的加速度分别多少?
2、前8秒内物体做匀变速直线运动吗?为什么?如何用自己的话比较准确的描述物体在0~8秒内的运动情况?
3、根据图象可知物体在0~6秒内的加速度和速度的变化,你能得出什么样的结论?
0
t
v
某物体的v-t图象如下,问:
思考与讨论
1、此物体做匀加速直线运动吗?为什么?
t1
t2
2、请比较物体在t1和t2这两个时刻的加速度a1和a2的大小?
思考与讨论
普通的小型轿车和旅客列车,速度都能达到100 km/h。但是,它们起步后达到这样的速度所需的时间是不一样的。例如一辆小汽车在20 s内速度达到了100 km/h,而一列火车达到这个速度大约要用500 s。
谁的速度“增加”得比较快?它们的速度平均1 s各增加多少?
小汽车的速度“增加”得比较快!
20 s
速度0
100km/h(约28m/s)
速度平均1 s 增加为
500 s
速度0
100km/h(约28m/s)
速度平均1 s 增加为
羚羊
猎豹
4 s
速度0
25m/s
速度平均1 s 增加为
4 s
速度0
30m/s
速度平均1 s 增加为
猎豹的速度“增加”得比较快!
炮弹的速度变化,比飞机的速度变化快得多!
30 s
速度0
300km/h(约83m/s)
速度平均1 s 增加为
0.005 s
速度0
250m/s
速度平均1 s 增加为
v1/m.s-1
△t/s
v2/m.s-1
△v/m·s-1
A. 自行车下坡
2
3
11
B. 公共汽车出站
0
3
6
C. 某舰艇出航
0
20
6
D. 火车出站
0
100
20
E. 飞机匀速飞行
300
10
300
9
6
0
6
20
谁的速度大?
谁的速度变化得快?
再举出一些例子,说明“速度大”、“速度变化大”、“速度变化得快”描述的是三种不同的情况。
谁的速度的变化量大?
v1/(m·s-1)
△t/s
v2/(m·s-1)
△v/ (m·s-1)
A.自行车下坡
2
3
11
B.公共汽车出站
0
3
6
C.某舰艇出航
0
20
6
D.火车出站
0
100
20
E.飞机匀速飞行
300
10
300
9
6
0
6
20
△v/△t(m·s-2)
3
2
0.3
0.2
0
你能从表中得到比较速度变化的快慢的方法吗?
速度的变化量跟发生这一变化所用时间的比值有何意义?
比值?v/?t越大, 速度的变化越快.
“速度大”、“速度变化大”、“速度变化得快”描述的是三种不同的情况。
“速度大”,是指位置变化快 。
“速度变化大”,是指末速度与初速度的差别大。
“速度变化得快” ,是指单位时间内速度变化大。
一、加速度
⒈ 定义:
v1----初速度(时间△t开始时的速度)
v2----末速度(时间△t末了时的速度)
⒉ 定义式:
a ----加速度(时间△t范围内的加速度)
⒊ 物理意义:描述速度变化快慢的物理量
速度的变化量跟发生这一变化所用时间的比值。
4、单位:国际单位—米/秒2 符号m/s2 读法:米每二次方秒
5、加速度是矢量,方向与速度变化量△v的方向相同
汽车的加速性能(制动距离)是反映汽车性能的重要指标.下列哪种汽车的加速性能最优越?
0~100km/h加速时间:
夏利15s
宝来10.5s
奔驰6.5s
宝马5.6s
F-1赛车2.3s.
一些运动物体的加速度
一些运动物体的加速度
速度很大,加速度很小
加速度很大,速度不太大
二、加速度方向与速度方向的关系(直线运动)
⒈ 速度的变化量△v
⑴ 定义: 末速度减去初速度
⑵ 定义式 △v = v2-v1
⑶ 作图法寻找 △v
Δ
v
v1
v2
Δ
v
v1
v2
① 加速直线运动
②减速直线运动
a
a
在直线运动中, a ,v共线
②图解法:以初速度的箭头为起点,以末速度的箭头为终点,做出一个新的有向线段,它就表示速度的变化量△V。
这个计算法则对速度不在一条直线上也是正确的。
速度的变化量是矢量。
V2
V1
△V
V1
V2
△V
如图所示,求小球在碰撞过程中,速度的变化量?
3m/s
3m/s
正方向
1. 规定某一方向(一般以初速度方向)为正方向
2.表示已知量:已知量与规定正方向相同,计为正;相反,记为负
速度的变化量等于末速度减初速度,
即Δv=v2-v1 =-3m/s-3m/s=-6m/s,
v1 =3m/s,
v2=-3m/s,
3.求解的结果:矢量的正负只表示方向(与规定正方向同向还是反向),不表示大小
一条直线上运动问题的解决方法:
二、加速度方向与速度方向的关系(直线运动)
⒉ 加速度 (a = △v/△t )的方向
在变速直线运动中,若以初速度v1方向为正方向,
① 加速直线运动,a ___0,a的方向 ;
② 减速直线运动,a ___0, a的方向 。
结论:加速度方向和速度变化量△v的方向相同,与速度方向无关。
>
与v1方向相同
<
与v1方向相反
⒈ 速度的变化量△v
理解加速度的概念
物体做直线运动,初速度为v1,经过时间?t=1s,速度变为v2。分别求出下述情况的加速度。
1.v1=2m/s,向右, v2=5m/s;
2.v1=5m/s,向右, v2=2m/s;
3.v1=2m/s,向右, v2=-2m/s;
注意矢量性,要回答方向!!
以初速度方向为正方向:
三、加速度大小与速度大小的关系
⒈ 速度大,加速度不一定大;
⒉ 加速度为零时,速度可以不为零;
结论:加速度与速度没有必然联系。
加速度大,速度不一定大。
速度为零时,加速度可以不为零。
速度变化量大,加速度不一定大;
结论:加速度与速度变化量大小没有必然联系。
四、加速度大小与速度变化量大小的关系
加速度大,速度变化量不一定大。
瞬时速度
瞬时加速度
取很小很小的值 0
取很小很小的值 0
五、平均加速度和瞬时加速度
1、平均加速度:粗略描述速度变化快慢
公式: a=? v / ? t
2、瞬时加速度:精确描述每一时刻速度变化快慢
3、匀变速运动:加速度不变的沿着一条直线的运动。
匀变速运动中,平均加速度与瞬时加速度相等。
六、变化率
⒈ 定义:
⒉ 物理意义:
某量D的变化量△D与发生这个变化所用的时间△t 的比值△D/△t ,叫做这个量的变化率。
描述某量D的变化快慢,不表示某量D的变化量△D的大小。
快慢
速度
变化
加速度
速度
快慢
位置
变化
速度描述物体位置变化的快慢,即位置的变化率;
△ x
v = ——
△t
位置
速度
变化的快慢
变化的快慢
加速度
△ v
a = ——
△t
加速度描述速度变化的快慢,即速度的变化率。
速度V
速度变化量ΔV
加速度a
定义式
Δv= v-v0
意义
表物体运动(位置变化)的快慢
表速度的变化
表示速度变化的快慢
a大,速度变化快
单位
m/s
m/s
m/s2
方向
质点运动的方向即运动轨迹的切线方向
由Δv= v-v0决定的方向,可能与v0方向相同也可能与v0方向相反
与速度的变化Δv方向相同,而与速度方向无关
大小
1 位移与时间的比值
2位置对时间的变化率
3X-t坐标系中曲线的斜率大小
Δv= v-v0
1速度变化量与时间的比值
2 速度对时间的变化率
3 v-t坐标系中曲线的斜率大小
与时间的关系
与时刻对应
状态量
与时间间隔对应
过程量
瞬时加速度对应时刻平均加速度对应时间
联系
⑴、 a的大小、方向与速度的大小、方向没有直接的关系。(2) a的大小与Δv的大小没有直接的关系。但是a的方向与Δv的方向总是相同的。(3)有了a,速度一定要变化,物体是加速、减速不是由加速度的正负决定,而是由a与v的关系定: a与v同向,加速;a与v反向,减速
比较位置X、位移△X、速度V的关系
?
位置X
位移△X
速度V
定义式
X=?
△X=X2-X1
△X/△t
意义
表示物体的位置
表示位置改变
表示位置改变的快慢
大小
用坐标表示
坐标的差
运动快慢,表示位置变化的快慢,位置变化率
方向
从初位置指向末位置
与位移△X同向
单位
m
m
m/s
与时间的关系
与时刻对应
状态量
与时间间隔对应
过程量
平均速度对应时间
瞬时速度对应时刻
1、若vt>v0,则△v ____0,
物体做_______运动;
2、若vt
练习:在直线运动中
表达式: △v = vt-v0
3、 加速度 (a = △v/ △t )
以速度方向为正,① 加速运动,a ___ 0
② 减速运动,a ___ 0
4、加速度是____量
① 加速运动,a的方向____________
② 减速运动,a的方向____________
5、匀变速直线运动:是_____不变的运动。
a、b分别是两个物体运动的v-t图像。哪个物体运动的加速度较大?为什么?
七、从v-t 图象看加速度
?t
?v
t1
v1
t2
v2
b
v(m/s)
O
a
从曲线的倾斜程度就能判断加速度的大小,
比值?v/?t就是加速度的数值。
小三角形水平的直角边代表时间间隔?t,竖直直角边代表速度的变化量?v 。
t/s
⒈ 从v-t图象的—————— 看加速度的大小;
⒉ 由v-t图像计算加速度的大小。
六、从v-t 图象看加速度
倾斜程度(斜率)
t/s
O
v/m·s-1
10
15
5
4
6
2
A
B
思考:A、B两物体的速度哪个变化快?
A物体的加速度为 ;
B物体的加速度为 。
0.5m/s2
0.2m/s2
v-t 图像的斜率就是加速度
七、从v-t 图象看加速度
减速运动的v-t图像应该怎样画呢?
课堂小结:
速度的改变
速度
加速度
表示运动的快慢
表示速度的变化
表示速度变化的快慢
v
Δv=vt-v0
1、定义:速度的改变跟发生这一改变所用的时间的比值
2、公式:
4、矢量性:加速度的方向与速度变化的方向相同
5、匀变速直线运动的特点:加速度是恒定的
3、单位:m/s
2
⑴速度大,加速度不一定大;
加速度大, 速度不一定大。
⑵加速度为零,速度不一定为零;
速度为零,加速度也不一定为零
2、加速度和速度的区别
①它们的含义不同
速度描述的是位置变化的快慢
加速度描述的是速度变化的快慢
②看它们的大小情况
加速度大小和速度大小没必然联系;但 若a不为零,V一定变化
加速度 a = ( vt - v0 ) / △t
某一物理量的变化跟发生这一变化所用的时间的比值,叫做该量对时间的变化率。加速度是速度对时间的 变化率
3、加速度和速度的变化量(Δv = vt - vo):
速度的变化量表示速度改变了多少。等于物体末速度和初速度的矢量差(也为 矢量).
所以:速度变化量大,加速度不一定大;
a 与Δv 也无直接联系
加速度就是增加的速度吗?
加速度只能针对加速运动而言吗? 对减速运动适合吗?
如何表示减速运动的加速度呢?
思考与讨论
1)速度大,加速度也一定大吗?
3)速度变化量大,加速度也一定大吗?
2)加速度大,速度也一定大吗?
速度大,加速度不一定大;加速度大,速度不一定大.
速度变化量大,加速度不一定大.
思考与讨论
4)加速度为零时,速度也一定为零吗?
5)速度为零时,加速度也一定为零吗?
加速度为零,速度可以不为零;
速度为零,加速度可以不为零.
①加速度方向和初速度方向相同
速度增加
加速运动
②加速度方向和初速度方向相反
速度减小
减速运动
6)加速度增加的运动是加速运动,加速度减小的运动是减速运动.这种认识对吗?
(如果不对,你认为应该怎样根据加速度判断物体的速度是增加还是减小?)
判断下列说法是否正确,并举例说明:
①速度大,加速度不一定大;
②加速度大,速度不一定大;
③速度变化量大,加速度不一定大;
④加速度为零,速度不一定为零;
⑤速度为零,加速度可以不为零。
说明:加速度是速度的变化率,与速度大小无直接关系。
如:匀速
如:启动
如:t大
如:匀速
如:启动
⑴ 飞机起飞前在地面上滑行,可以在30s内,速度由零增加到81m/s。那么,飞机起飞前的加速度为多少?
⑵汽车急刹车时,可以在3秒内速度由18m/s减小到零。那么,汽车急刹车时的加速度为多少?
加速度的正、负的含义是什么呢?
以初速度方向为正方向:
O
v/m·s-1
t/s
4
6
2
4
6
2
1、前2s内的加速度为
2、2s—4s的加速度为
0
3、4s—6s的加速度为
注意:加速度为负值表示速度减小,此时,加速度方向与速度方向相反
D
⒈ 下列说法正确的是 ( )
A. 物体速度改变量大,其加速度一定大
B. 物体有加速度时,速度就增大
C. 物体的加速度大,速度一定大
D. 物体速度的变化率大,加速度一定大
⒉ 关于加速度的含义,下列说法正确的是( )
A. 加速度表示速度的增加
B. 加速度表示速度变化
C. 加速度表示速度变化快慢
D. 加速度表示速度变化的大小
C
⒊ 下列说法正确的是:
A. 加速度增大,速度一定增大( )
B. 速度变化越大,加速度越大
C. 物体有加速度,速度就增大
D. 物体的速度很大,加速度可能为零
D
⒋ 以下关于加速度的说法中,正确的是( )
A. 加速度为0的物体一定处于静止状态
B. 物体的加速度减小,其速度必随之减小
C. 物体的加速度增加,其速度不一定增大
D. 物体的加速度越大,其速度变化越快
CD
⒌ 关于速度、速度改变量、加速度,正确的说法是:
A、物体运动的速度改变量很大,它的加速度一定 很大
B、速度很大的物体,其加速度可以很小,可以为零
C、某时刻物体的速度为零,其加速度不可能为零
D、加速度很大时,运动物体的速度一定很大
B
C
⒍ 一个物体的加速度为零,则该物体一定是 ( )
A. 静止不动
B. 匀速直线运动
C. 静止或匀速直线运动
D. 做速度大小不变的运动
D
⒎ 下列关于速度和加速度的叙述中,结论正确的是
A. 物体的速度越大,它的加速度也一定越大
B. 物体运动的加速度为零,它的速度也为零
C. 物体运动的速度改变越大,它的加速度也一定越大
D. 加速度的大小就是速度对时间的变化率的大小
BD
⒏ 若汽车的加速度方向与速度方向一致,当加速度减小时,则 ( )
A.汽车的速度也减小
B.汽车的速度仍在增大
C.当加速度减小到零时,汽车静止
D. 当加速度减小到零时,汽车的速度达到最大
10. 甲乙两物体的速度图象如图所示,由图可知a甲= ,a乙= ;t = 时,v甲= v乙;若
t = 时甲追上乙,再过1s乙在甲 (填前、后)方。
v/m.s-1
t/s
o
8
4
4
8
甲
乙
0
-1m/s-2
4s
8s
后
专题:
V-t图象中的加速度
1、V-t图象上的各个“点”表示什么意义?
关于v-t图象的物理意义:
t1
v1
t2
v2
表示:某时刻物体的速度
2、v-t图象上的“线”反映什么?
表示:速度随时间变化的规律
根据v-t图象判断物体的运动情况:
0
t
v
(B)
x
o
以v0速度做匀速直线
x
o
初速度为零的加速直线
0
t
v
(A)
v0
0
t
v
(C)
v0
0
t
v
(D)
v0
x
o
以初速度v0做加速直线
x
o
以初速度v0做减速直线
0
t
v
(E)
t0
-2
2
-1
1
t2
t1
0
t
v
(F)
2
-2
t0
t1
x
o
x
o
正方向减速
-2
0
负向减速
正方向加速
2
0
负方向加速
根据v-t图象求物体的加速度:
v/m.s-1
t/s
0
1
t1
t2
v1
v2
v0
?v1
?t1
思考1:能根据v-t图象求物体t1~t2和t0~t2时间内的加速度吗?如何求?
思考2:你认为此物体在0~t1内的加速度和t1~t2的加速度有什么关系?为什么?
?v2
?t2
思考3:你能根据v-t图象定性判断物体加速度的大小吗?怎么判断?
2
a2>a1
结论:
根据v-t图象求物体的加速度:
v/m.s-1
t/s
0
1
t1
t2
v1
v2
v0
2
a2>a1
2、加速度不变的运动叫匀变速运动;匀变速直线运动的v-t图象是一条倾斜的直线。
1、可以根据图线的倾斜程度来定性判断变速运动加速度的大小。
3
3、匀变速直线运动包括匀加速和匀减速直线运动。
a2>a3>a1
练习:某物体的运动v-t图象如下,问:
v/m.s-1
t/s
0
2
4
10
14
6
8
1、物体在各个时间段内的加速度分别多少?
2、前8秒内物体做匀变速直线运动吗?为什么?如何用自己的话比较准确的描述物体在0~8秒内的运动情况?
3、根据图象可知物体在0~6秒内的加速度和速度的变化,你能得出什么样的结论?
0
t
v
某物体的v-t图象如下,问:
思考与讨论
1、此物体做匀加速直线运动吗?为什么?
t1
t2
2、请比较物体在t1和t2这两个时刻的加速度a1和a2的大小?
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
