2011-2012学年八年级数学同步练习题及答案:作轴对称图形
文档属性
| 名称 | 2011-2012学年八年级数学同步练习题及答案:作轴对称图形 |  | |
| 格式 | zip | ||
| 文件大小 | 39.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-16 23:57:49 | ||
图片预览

文档简介
2011-2012学年八年级数学同步练习题及答案:作轴对称图形
【模拟试题】(答题时间:40分钟)
一、 选择题
1. 下列说法错误的是 ( )
A. 关于某直线对称的两个图形一定能完全重合
B. 全等的两个三角形一定关于某直线对称
C. 轴对称图形的对称轴至少有一条
D. 线段是轴对称图形
2. 轴对称图形的对称轴是 ( )
A. 直线 B. 线段 C. 射线 D. 以上都有可能
3. 下面各组点关于y轴对称的是 ( )
A. (0,10)与(0,-10) B. (-3,-2)与(3,-2)
C. (-3,-2)与(3,2) D. (-3,-2)与(-3,2)
4. 下列图形中,不是轴对称图形的是 ( )
A. 一条线段 B. 两条相交直线
C. 有公共端点的两条相等的线段 D. 有公共端点的两条不相等的线段
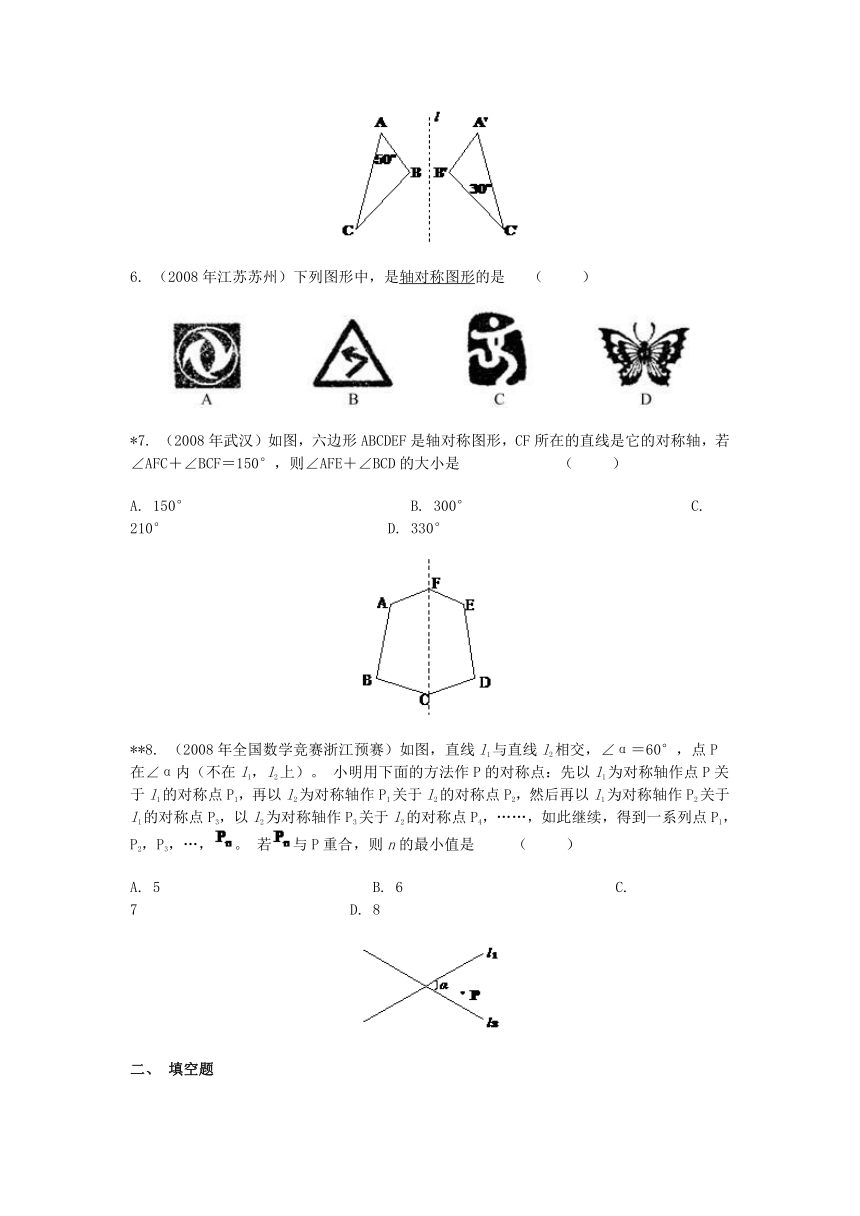
5. (2007年河南)如图,ΔABC与ΔA'B'C'关于直线l对称,则∠B的度数为 ( )
A. 30° B. 50° C. 90° D. 100°
6. (2008年江苏苏州)下列图形中,是轴对称图形的是 ( )
*7. (2008年武汉)如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是 ( )
A. 150° B. 300° C. 210° D. 330°
**8. (2008年全国数学竞赛浙江预赛)如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1,l2上)。 小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,……,如此继续,得到一系列点P1,P2,P3,…,。 若与P重合,则n的最小值是 ( )
A. 5 B. 6 C. 7 D. 8
二、 填空题
9. (2006年宜昌)从汽车的后视镜中看见某车车牌的后5位号码是,该车牌的后5位号码实际是__________。
10. 如图所示,是用笔尖扎重叠的纸得到成轴对称的图案,请根据图形写出:
(1)两组对应点__________和__________;
(2)两组对应线段__________和__________;
(3)两组对应角__________和__________。
11. 点A(-5,-6)与点B(5,-6)关于__________对称。
*12.(2007年四川内江)已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m=__________,n=__________。
三、 解答题
13. 画出下列各图形的所有对称轴。
14. 如图所示,作出△ABC关于直线l的对称三角形A'B'C'。
**15. (1)回答问题:①到线段两端点的距离相等的点在__________上;②到角的两边距离相等的点在__________上。
(2)根据(1)中的结论作图。
如图所示,求作一点P,使PC=PD,且使点P到∠AOB的两边的距离相等。
**16. 如图所示,△ABC中,DE垂直平分线段AB,AE=5cm,△ACD的周长为17cm,求△ABC的周长。
四、 应用与探究题
17. 观察下图中的图形,虚线是不是它们的对称轴?你是如何验证的?
**18. 如图,草原上两个居民点A、B在河流l的同侧,一辆汽车从A出发到B,途中需到河边加水,汽车在哪一点加水,可使行驶的路程最短?
【试题答案】
一、 选择题
1. B 2. A 3. B 4。 D 5。 D 6。 D 7。 B 8。 B
二、 填空题
9. BA629
10. 答案不唯一,(1)A与D,B与E(2)AB与DE,AC与DF(3)∠A与∠D,∠B与∠E
11. y轴 12. 3,-4
三、 解答题
13. 如图所示:
14. 如图所示:
15. (1)①这条线段的垂直平分线;②这个角的平分线。 (2)①连结CD,②作线段CD的垂直平分线a,③作∠AOB的平分线OM,OM交a于点P。 点P就是所求作的点。
16. 解:∵DE垂直平分线段AB,∴DA=DB,AE=BE。 ∵AE=5cm,∴BE=5cm,∴AB=AE+BE=10cm。 ∵△ABC的周长=CA+CD+DB+AB,△ACD的周长=CA+CD+AD=CA+CD+DB=17cm,∴△ABC的周长=17+10=27cm。
四、 应用与探究题
17. 将这些图形分别沿图中的虚线对折,如果折叠后两边能够完全重合,那么这个图形就是轴对称图形,这条虚线就是它的对称轴;如果折叠后两边不能够完全重合,那么这条虚线就不是它的对称轴(不一定不是轴对称图形,如图(2)不是轴对称图形,图(3)是轴对称图形)。 用上述方法验证得:图(1)和(3)中的虚线是它们各自的对称轴,图(2)和(4)中的虚线不是它们各自的对称轴。
18. 如图所示,①作点B关于直线l的对称点,②连结,交直线l于点C. 点C就是所求的点。
【模拟试题】(答题时间:40分钟)
一、 选择题
1. 下列说法错误的是 ( )
A. 关于某直线对称的两个图形一定能完全重合
B. 全等的两个三角形一定关于某直线对称
C. 轴对称图形的对称轴至少有一条
D. 线段是轴对称图形
2. 轴对称图形的对称轴是 ( )
A. 直线 B. 线段 C. 射线 D. 以上都有可能
3. 下面各组点关于y轴对称的是 ( )
A. (0,10)与(0,-10) B. (-3,-2)与(3,-2)
C. (-3,-2)与(3,2) D. (-3,-2)与(-3,2)
4. 下列图形中,不是轴对称图形的是 ( )
A. 一条线段 B. 两条相交直线
C. 有公共端点的两条相等的线段 D. 有公共端点的两条不相等的线段
5. (2007年河南)如图,ΔABC与ΔA'B'C'关于直线l对称,则∠B的度数为 ( )
A. 30° B. 50° C. 90° D. 100°
6. (2008年江苏苏州)下列图形中,是轴对称图形的是 ( )
*7. (2008年武汉)如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是 ( )
A. 150° B. 300° C. 210° D. 330°
**8. (2008年全国数学竞赛浙江预赛)如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1,l2上)。 小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,……,如此继续,得到一系列点P1,P2,P3,…,。 若与P重合,则n的最小值是 ( )
A. 5 B. 6 C. 7 D. 8
二、 填空题
9. (2006年宜昌)从汽车的后视镜中看见某车车牌的后5位号码是,该车牌的后5位号码实际是__________。
10. 如图所示,是用笔尖扎重叠的纸得到成轴对称的图案,请根据图形写出:
(1)两组对应点__________和__________;
(2)两组对应线段__________和__________;
(3)两组对应角__________和__________。
11. 点A(-5,-6)与点B(5,-6)关于__________对称。
*12.(2007年四川内江)已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m=__________,n=__________。
三、 解答题
13. 画出下列各图形的所有对称轴。
14. 如图所示,作出△ABC关于直线l的对称三角形A'B'C'。
**15. (1)回答问题:①到线段两端点的距离相等的点在__________上;②到角的两边距离相等的点在__________上。
(2)根据(1)中的结论作图。
如图所示,求作一点P,使PC=PD,且使点P到∠AOB的两边的距离相等。
**16. 如图所示,△ABC中,DE垂直平分线段AB,AE=5cm,△ACD的周长为17cm,求△ABC的周长。
四、 应用与探究题
17. 观察下图中的图形,虚线是不是它们的对称轴?你是如何验证的?
**18. 如图,草原上两个居民点A、B在河流l的同侧,一辆汽车从A出发到B,途中需到河边加水,汽车在哪一点加水,可使行驶的路程最短?
【试题答案】
一、 选择题
1. B 2. A 3. B 4。 D 5。 D 6。 D 7。 B 8。 B
二、 填空题
9. BA629
10. 答案不唯一,(1)A与D,B与E(2)AB与DE,AC与DF(3)∠A与∠D,∠B与∠E
11. y轴 12. 3,-4
三、 解答题
13. 如图所示:
14. 如图所示:
15. (1)①这条线段的垂直平分线;②这个角的平分线。 (2)①连结CD,②作线段CD的垂直平分线a,③作∠AOB的平分线OM,OM交a于点P。 点P就是所求作的点。
16. 解:∵DE垂直平分线段AB,∴DA=DB,AE=BE。 ∵AE=5cm,∴BE=5cm,∴AB=AE+BE=10cm。 ∵△ABC的周长=CA+CD+DB+AB,△ACD的周长=CA+CD+AD=CA+CD+DB=17cm,∴△ABC的周长=17+10=27cm。
四、 应用与探究题
17. 将这些图形分别沿图中的虚线对折,如果折叠后两边能够完全重合,那么这个图形就是轴对称图形,这条虚线就是它的对称轴;如果折叠后两边不能够完全重合,那么这条虚线就不是它的对称轴(不一定不是轴对称图形,如图(2)不是轴对称图形,图(3)是轴对称图形)。 用上述方法验证得:图(1)和(3)中的虚线是它们各自的对称轴,图(2)和(4)中的虚线不是它们各自的对称轴。
18. 如图所示,①作点B关于直线l的对称点,②连结,交直线l于点C. 点C就是所求的点。
