北师大版七年级数学上册4.1 线段、射线、直线同步练习(Word版含答案)
文档属性
| 名称 | 北师大版七年级数学上册4.1 线段、射线、直线同步练习(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 224.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 09:33:20 | ||
图片预览

文档简介
4.1 线段、射线、直线
1.下列说法中正确的是( )
A.射线是直线的一半
B.线段是射线的一半
C.直线比射线长
D.线段可以看成是直线上的一部分
2.图1中直线AB,射线CD,线段MN能够相交的是( )
图1
3.下列语句中正确的个数是( )
①画直线AB=3
cm;②直线AB与直线BA是同一条直线,所以射线AB与射线BA也是同一条射线;③延长射线OA;④线段AB与线段BA是同一条线段.
A.0
B.1
C.2
D.3
4.如图2,C是线段BD上的点,有下列结论:①图中共有5条线段;②射线BD和射线DB是同一条射线;③直线BC和直线BD是同一条直线;④射线AB,AC,AD的端点相同.其中正确的结论是( )
图2
A.②④
B.③④
C.②③
D.①③
5.下列现象:
(1)经过刨平的木板上的两个点,就能弹出一条笔直的墨线;
(2)从A地到B地架设电线,总是尽可能沿着线段AB架设;
(3)植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
(4)把弯曲的公路改直,就能缩短路程.
其中,能用“两点确定一条直线”来解释的现象有( )
A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(3)(4)
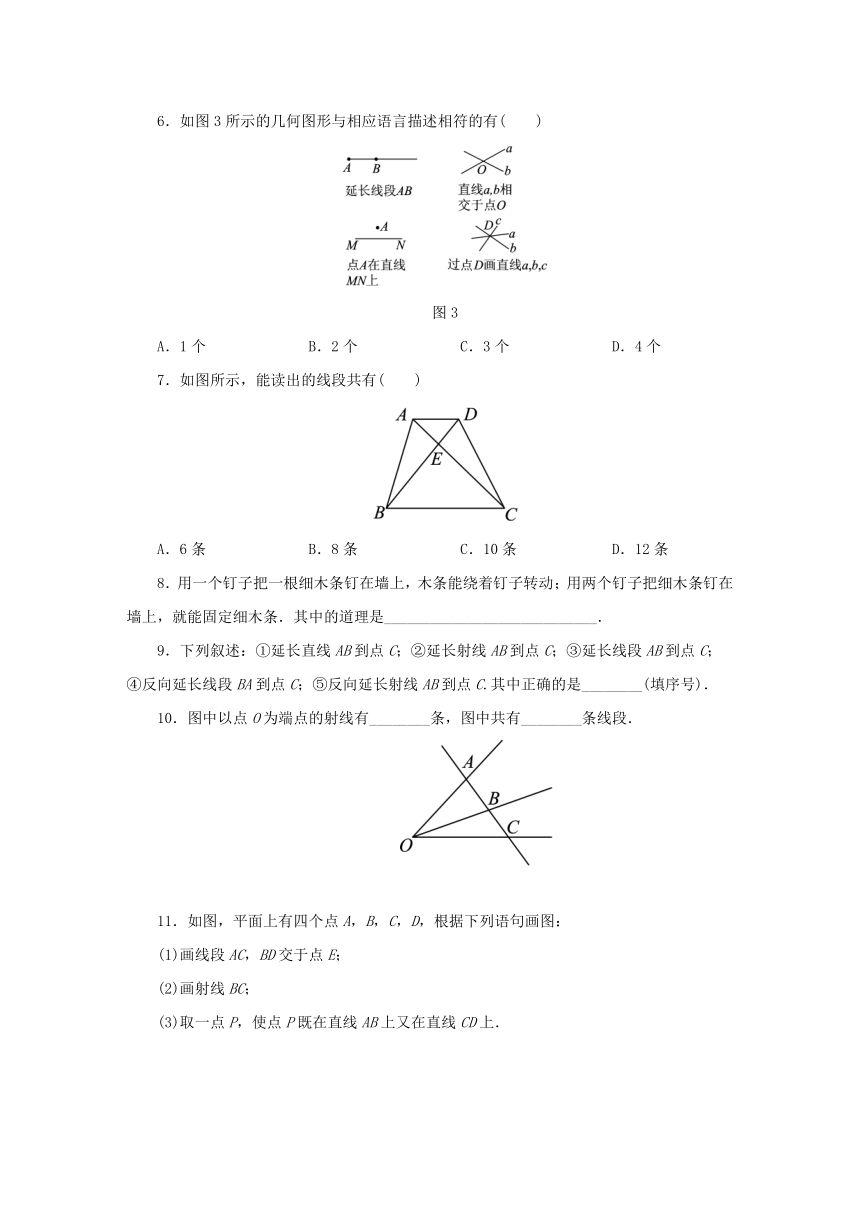
6.如图3所示的几何图形与相应语言描述相符的有( )
图3
A.1个
B.2个
C.3个
D.4个
7.如图所示,能读出的线段共有( )
A.6条
B.8条
C.10条
D.12条
8.用一个钉子把一根细木条钉在墙上,木条能绕着钉子转动;用两个钉子把细木条钉在墙上,就能固定细木条.其中的道理是____________________________.
9.下列叙述:①延长直线AB到点C;②延长射线AB到点C;③延长线段AB到点C;
④反向延长线段BA到点C;⑤反向延长射线AB到点C.其中正确的是________(填序号).
10.图中以点O为端点的射线有________条,图中共有________条线段.
11.如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)画线段AC,BD交于点E;
(2)画射线BC;
(3)取一点P,使点P既在直线AB上又在直线CD上.
12.实践与应用:
一张饼放在桌子上,用刀从上往下切下去,一刀可以切成2块,2刀最多可以切成4块,3刀最多可以切成7块,4刀最多可以切成11块(如图7).
图7
上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题,有没有规律呢?请先进行试验,然后回答以下问题.
(1)填表:
直线条数
1
2
3
4
5
6
…
分成的最多块数
2
4
7
11
…
(2)直接写出n条直线最多把平面分成的块数(用含n的式子表示).
13.(1)观察思考:
如图8,线段AB上有两个点C,D,请分别写出以点A,B,C,D为端点的线段,并计算图中共有多少条线段;
图8
(2)模型构建:
如果线段上有m个点(包括线段的两个端点),那么该线段上共有多少条线段?请说明你结论的正确性.
(3)拓展应用:
8名同学参加班上组织的象棋比赛,比赛采用单循环制(即每两名同学之间都要进行一场比赛),那么一共要进行多少场比赛?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
.
答案
1.D 2.D
3.B 4.B 5.B
6.C 7.C
8.经过一点有无数条直线,经过两点有且只有一条直线
9.③④⑤
10.3 6
11.解:如图所示.
12.解:设Sn为n条直线最多把平面分成的块数.(1)当n=5时,S5=1+1+2+3+
4+5=16;当n=6时,S6=1+1+2+3+4+5+6=22.
故填入表格的答案为16,22.
(2)Sn=1+1+2+3+…+n=1+.
13.解:(1)以点A为端点的线段有AB,AC,AD;
以点B为端点的线段有BA,BC,BD;
以点C为端点的线段有CA,CB,CD;
以点D为端点的线段有DA,DB,DC.
重复的线段有6条,所以共有6条线段.
(2)如果线段上有m个点(包括线段的两个端点),那么该线段上共有条线段.
理由:线段上有m个点(包括线段的两个端点),过每一个点都可以作(m-1)条线段,一共能作m(m-1)条线段,但由于线段端点的无序性,正好每条线段都被重复计算了一次,所以该线段上共有条线段.
(3)把8名同学看成直线上的8个点,每两名同学之间的一场比赛看成一条线段.
直线上8个点所构成的线段条数就等于比赛的场数,因此一共要进行=28(场)比赛.
1.下列说法中正确的是( )
A.射线是直线的一半
B.线段是射线的一半
C.直线比射线长
D.线段可以看成是直线上的一部分
2.图1中直线AB,射线CD,线段MN能够相交的是( )
图1
3.下列语句中正确的个数是( )
①画直线AB=3
cm;②直线AB与直线BA是同一条直线,所以射线AB与射线BA也是同一条射线;③延长射线OA;④线段AB与线段BA是同一条线段.
A.0
B.1
C.2
D.3
4.如图2,C是线段BD上的点,有下列结论:①图中共有5条线段;②射线BD和射线DB是同一条射线;③直线BC和直线BD是同一条直线;④射线AB,AC,AD的端点相同.其中正确的结论是( )
图2
A.②④
B.③④
C.②③
D.①③
5.下列现象:
(1)经过刨平的木板上的两个点,就能弹出一条笔直的墨线;
(2)从A地到B地架设电线,总是尽可能沿着线段AB架设;
(3)植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
(4)把弯曲的公路改直,就能缩短路程.
其中,能用“两点确定一条直线”来解释的现象有( )
A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(3)(4)
6.如图3所示的几何图形与相应语言描述相符的有( )
图3
A.1个
B.2个
C.3个
D.4个
7.如图所示,能读出的线段共有( )
A.6条
B.8条
C.10条
D.12条
8.用一个钉子把一根细木条钉在墙上,木条能绕着钉子转动;用两个钉子把细木条钉在墙上,就能固定细木条.其中的道理是____________________________.
9.下列叙述:①延长直线AB到点C;②延长射线AB到点C;③延长线段AB到点C;
④反向延长线段BA到点C;⑤反向延长射线AB到点C.其中正确的是________(填序号).
10.图中以点O为端点的射线有________条,图中共有________条线段.
11.如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)画线段AC,BD交于点E;
(2)画射线BC;
(3)取一点P,使点P既在直线AB上又在直线CD上.
12.实践与应用:
一张饼放在桌子上,用刀从上往下切下去,一刀可以切成2块,2刀最多可以切成4块,3刀最多可以切成7块,4刀最多可以切成11块(如图7).
图7
上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题,有没有规律呢?请先进行试验,然后回答以下问题.
(1)填表:
直线条数
1
2
3
4
5
6
…
分成的最多块数
2
4
7
11
…
(2)直接写出n条直线最多把平面分成的块数(用含n的式子表示).
13.(1)观察思考:
如图8,线段AB上有两个点C,D,请分别写出以点A,B,C,D为端点的线段,并计算图中共有多少条线段;
图8
(2)模型构建:
如果线段上有m个点(包括线段的两个端点),那么该线段上共有多少条线段?请说明你结论的正确性.
(3)拓展应用:
8名同学参加班上组织的象棋比赛,比赛采用单循环制(即每两名同学之间都要进行一场比赛),那么一共要进行多少场比赛?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
.
答案
1.D 2.D
3.B 4.B 5.B
6.C 7.C
8.经过一点有无数条直线,经过两点有且只有一条直线
9.③④⑤
10.3 6
11.解:如图所示.
12.解:设Sn为n条直线最多把平面分成的块数.(1)当n=5时,S5=1+1+2+3+
4+5=16;当n=6时,S6=1+1+2+3+4+5+6=22.
故填入表格的答案为16,22.
(2)Sn=1+1+2+3+…+n=1+.
13.解:(1)以点A为端点的线段有AB,AC,AD;
以点B为端点的线段有BA,BC,BD;
以点C为端点的线段有CA,CB,CD;
以点D为端点的线段有DA,DB,DC.
重复的线段有6条,所以共有6条线段.
(2)如果线段上有m个点(包括线段的两个端点),那么该线段上共有条线段.
理由:线段上有m个点(包括线段的两个端点),过每一个点都可以作(m-1)条线段,一共能作m(m-1)条线段,但由于线段端点的无序性,正好每条线段都被重复计算了一次,所以该线段上共有条线段.
(3)把8名同学看成直线上的8个点,每两名同学之间的一场比赛看成一条线段.
直线上8个点所构成的线段条数就等于比赛的场数,因此一共要进行=28(场)比赛.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
