(整数值)随机数的产生(说课)
图片预览







文档简介
(共46张PPT)
(整数值)随机数的产生
(random numbers)
(人教版A版《必修3》P130-132 )
教 学 目 标
重 点 难 点
教 学 评 价
教 材 分 析
教 学 过 程
教 法 手 段
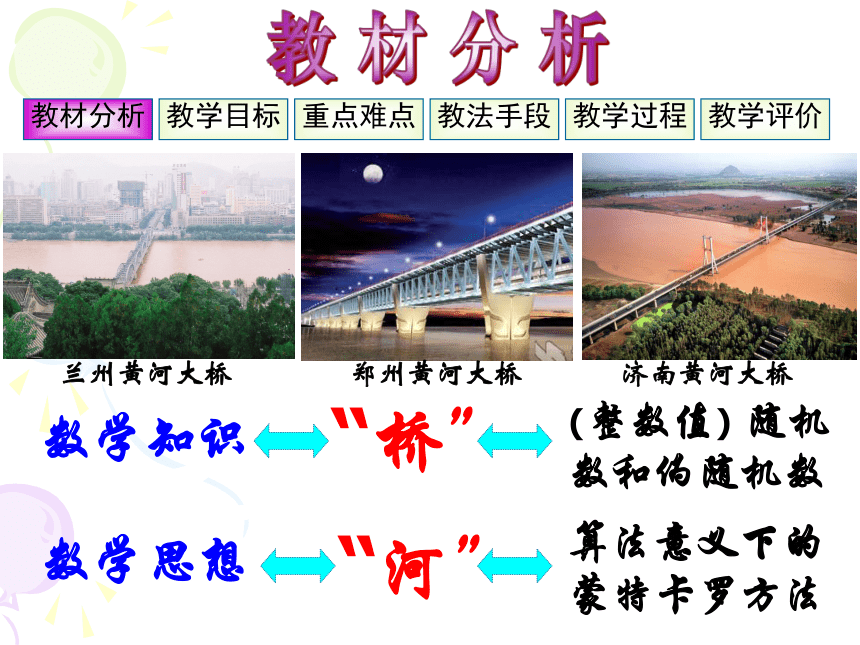
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
兰州黄河大桥
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
郑州黄河大桥
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
济南黄河大桥
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
兰州黄河大桥 郑州黄河大桥 济南黄河大桥
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
兰州黄河大桥 郑州黄河大桥 济南黄河大桥
“河”
数学知识
数学思想
算法意义下的蒙特卡罗方法
“桥”
(整数值) 随机数和伪随机数
算 法 意 义 下 的 蒙 特 卡 罗 方 法 之 “河”
算法结构
古典概型
随机数
伪随机数
几何概型
均匀随机数
二项分布
将学知识
已学知识
本节知识
教学评价
教学过程
教法手段
重点难点
教学目标
教材分析
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
随机数、伪随机数
为什么……
蒙特卡罗方法
算法的思想
(整数值)随机数和伪随机数是“桥”,而算法意义下的蒙特卡罗方法是“河”.
“桥”
“河”
教材目标
教材分析
重点难点
教法手段
教学过程
教学评价
(1)明确(整数值)随机数及伪随机数的概念;
(2)会用信息技术工具产生(整数值)随机数(实际上是伪随机数);
(3)通过具体案例理解蒙特卡罗方法(随机模拟方法),能针对具体的随机事件设计概率模型,并通过蒙特卡罗方法得出随机事件的概率的估计值.
(4)在信息技术环境下,通过算法解决大量重复模拟试验中的数据统计问题,实现计算随机事件的概率的估计值,并由此进一步体会算法思想与随机模拟方法.
重点难点
教学目标
教材分析
教法手段
教学过程
教学评价
教学重点
通过具体案例理解蒙特卡罗方法,并用算法的思想实现计算随机事件的概率的估计值这个过程.
重点难点
教学目标
教材分析
教法手段
教学过程
教学评价
教学难点
对于很难列举全部基本事件的古典概型或非古典概型中的随机事件(如概率为40%的下雨事件),建立什么样的概率模型来模拟,通过怎样的步骤来进行随机模拟试验,这是本节课的教学难点之一.
重点难点
教学目标
教材分析
教法手段
教学过程
教学评价
教学难点
如何通过算法使学生更好地体会蒙特卡罗方法是本节课的教学难点之二.
教法手段
教学目标
重点难点
教材分析
教学过程
教学评价
教师启发下的学生自主探究
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
以问题为主线,以学生为主体,以探究为途径,借助于信息技术,将数学的知识之“桥”与思想之“河”紧密地结合在一起.
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题1】天气预报说,在今后的三天中,每一天下雨的概率均为40%,这三天中恰有两天下雨的概率是多少?
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
一方面,是使学生从“每一天下雨的概率均为40%”认识到非古典概型的客观存在性,同时感受到这不是一个用已经学过的知识就能解决的问题,为引入随机数及蒙特卡罗方法作铺垫;
另一方面,使学生明确本节课的主要问题的同时,激发学生的学习欲望,使整个教学过程都围绕这个问题展开.
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题2】将一个骰子掷1次,向上一面出现1点的概率是多少?如果将一个骰子掷1000次,向上一面出现1点的次数大约是多少?如果通过试验的方法,要估计(掷一个骰子1次)向上一面出现1点的概率,你会怎么做?
(1) 引导学生复习古典概型;
(2)体会用试验方法求出随机事件出现的频率,并以此来估计概率的方法,
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题2】将一个骰子掷1次,向上一面出现1点的概率是多少?如果将一个骰子掷1000次,向上一面出现1点的次数大约是多少?如果通过试验的方法,要估计(掷一个骰子1次)向上一面出现1点的概率,你会怎么做?
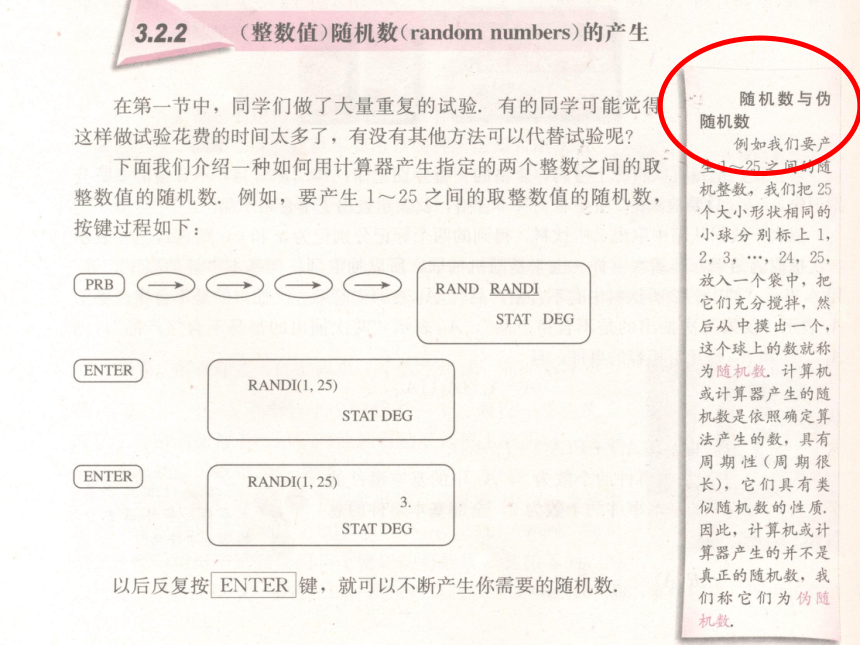
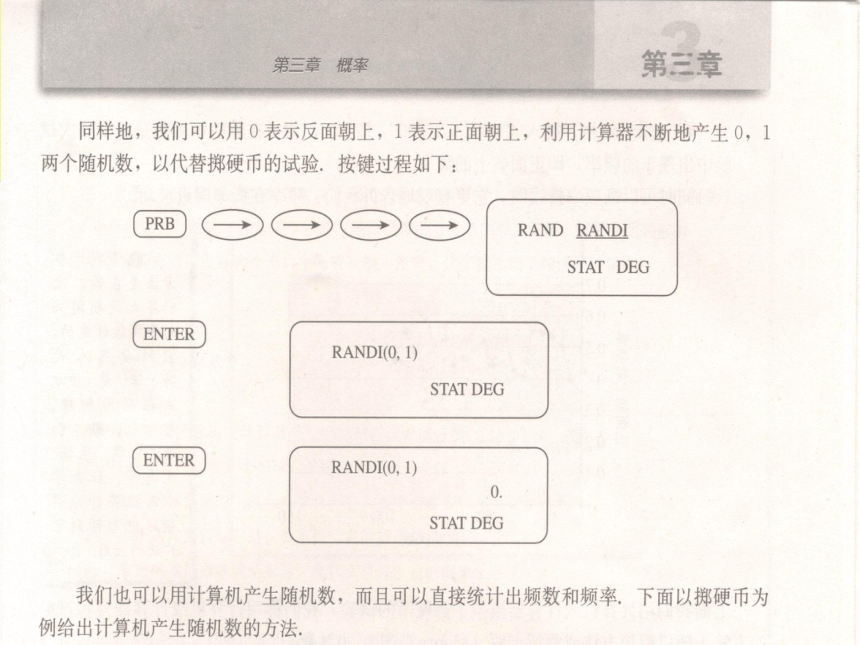
(3)认识到人工试验耗时费事,并由此引出随机数的概念,介绍用计算器产生伪随机数的方法. 能用算法思想处理问题,为解决【问题1 】服务.
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
开始
输入试验次数n
j=1; m=0
j<=n
x=rand(6)+1
x=1
m=m+1
j=j+1
输出m/n
结束
Y
N
Y
N
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题3】在一个盒子中装有形状大小完全一样,但分别标有 0,1,2,3,4,5,6,7,8,9的十个球.(1)从盒子中随机摸一球,球上所标的数字是什么?
(2)从盒子中随机摸一球,球上所标的数字不超过3的概率是多少?
(3)如何用计算器产生随机数去估计(2)中的概率,具体步骤怎样?
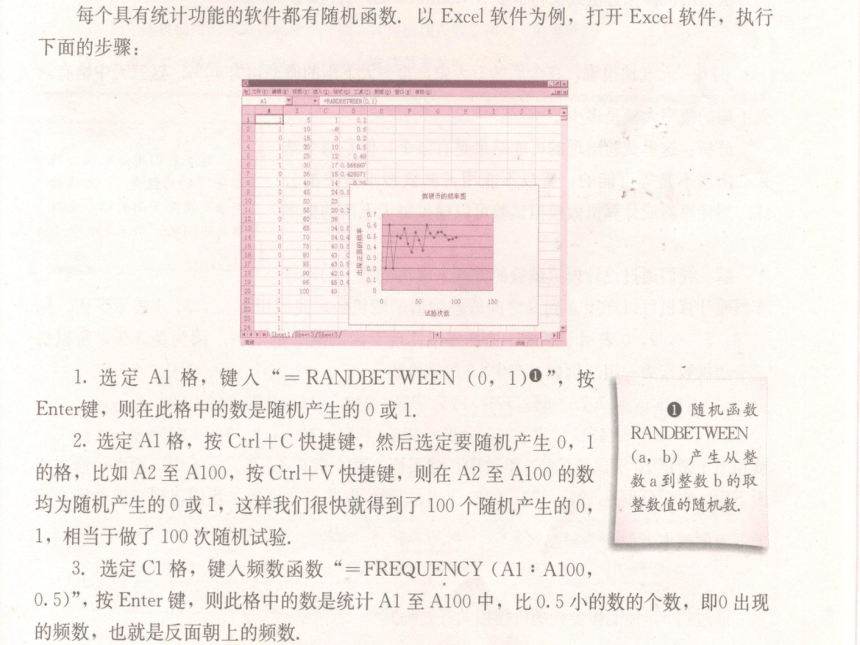
让学生经历用蒙特卡罗方法来估计古典概型中随机事件的概率的过程,体会在算法思想指导下,用蒙特卡罗方法计算概率估计值的重要意义.
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题3】在一个盒子中装有形状大小完全一样,但分别标有 0,1,2,3,4,5,6,7,8,9的十个球.
(1)从盒子中随机摸一球,球上所标的数字是什么?
(2)从盒子中随机摸一球,球上所标的数字不超过3的概率是多少?
(3)如何用计算器产生随机数去估计(2)中的概率,具体步骤怎样?
学生认识到从盒子中随机摸一球,球上所标的数字是随机数.
概率为40%,与问题1中的“下雨概率为40%”对应
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
开始
输入试验次数n
j=1; m=0
j<=n
x=rand(10)
x≤3
m=m+1
j=j+1
输出m/n
结束
Y
N
Y
N
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题4】问题1中的“每一天下雨的概率均为40%”是不好试验的,但由问题3我们知道“从标有0,1,2,3,4,5,6,7,8,9的十个球中随机摸出一球,球上所标的数字不超过3的概率也是40%”,这个属古典概型的摸球过程不仅可以试验,而且还可以通过计算器产生随机数来模拟试验.你能设计一个算法解决问题1吗?
使学生在解决前面问题的基础上,完整地体会蒙特卡罗方法,进一步体会算法思想的应用,彻底解决问题1.
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
师生活动
(1)教师:如果从十个球中摸出一球,球上的数字是0,1,2,3中的任何一个就表示下雨,否则就表示不下雨.
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
392
师生活动
(2)教师:那么三天的天气情况怎么模拟呢?
是
a=0:k=1
x=RAND(10)
x≤3
k≤3
m=m+1
a=2
m=0
a=a+1
k=k+1
否
否
否
是
是
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
师生活动
(3)教师:我们如何用计算机模拟的办法(即 蒙特卡罗的方法)来估计”三天中恰有两天下雨”的概率呢
(4)给学生思考与探索时间,然后与学生一起写出程序框图:
是
否
是
输入试验次数n
m=0:j=1
开始
a=0:k=1
x=RAND(10)
x≤3
j≤n
k≤3
j=j+1
a=2
m=m+1
输出m/n
结束
a=a+1
k=k+1
否
否
否
是
是
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
师生活动
(5)学生根据框图编出程序,在计算器上运行程序得出概率的估计值.
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
师生活动
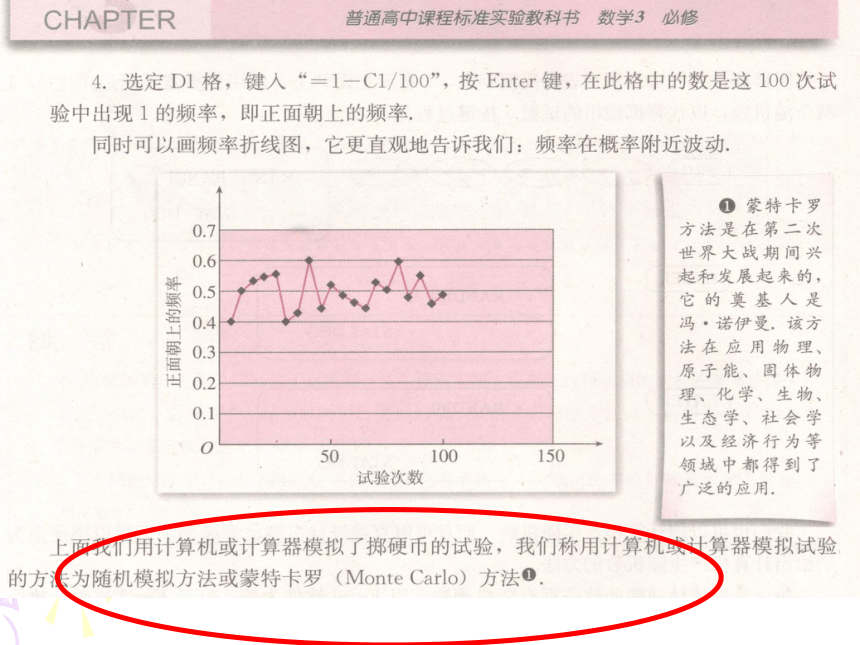
(6)重复运行上述程序,逐渐增大模拟试验的次数n,通过观察每次运行程序后所得结果,使学生认识到所求概率的估计值的近似程度是随着n的增大而提高的.
师生活动
(7)教师结合问题1的解决过程,介绍蒙特卡罗方法及其应用的广泛性.指出蒙特卡罗方法的基本原理、思想 以及基本步骤.
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题5】你能从用蒙特卡罗方法解决问题1的过程中,得出用于模拟的概率模型的基本特征吗?你是否可以建立另一个概率模型用于模拟问题1中的随机事件?
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
5
4
3
2
1
下雨
不下雨
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题6】你能举出一个用蒙特卡罗方法解决实际问题的实例吗?由你的实例说明使用蒙特卡罗方法时应该注意哪些方面?
让学生认识到用于模拟的概率模型不是唯一的,并通过建立另一个概率模型用于模拟试验,进一步体会蒙特卡罗方法的作用.
开拓学生视野,体会思想方法,小结本课内容 .
设计意图
教学评价
教学目标
重点难点
教法手段
教材分析
教学过程
探究作业: (即【问题1】的扩展研究)
天气预报说,在今后的三天中,每一天下雨的概率均为40%,那么在这三天中,有几天下雨的可能性大一些呢?
巩固学生对蒙特卡罗方法和算法思想的理解,让学生体会随机模拟的优点,使学生头脑中的思想之“河”流经更多的知识之“桥”,并使这条河更清澈,更流畅,更致远,……
设计意图
《 (整数值)随机数(random numbers)的产生 》
(整数值)随机数的产生
(random numbers)
(人教版A版《必修3》P130-132 )
教 学 目 标
重 点 难 点
教 学 评 价
教 材 分 析
教 学 过 程
教 法 手 段
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
兰州黄河大桥
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
郑州黄河大桥
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
济南黄河大桥
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
兰州黄河大桥 郑州黄河大桥 济南黄河大桥
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
兰州黄河大桥 郑州黄河大桥 济南黄河大桥
“河”
数学知识
数学思想
算法意义下的蒙特卡罗方法
“桥”
(整数值) 随机数和伪随机数
算 法 意 义 下 的 蒙 特 卡 罗 方 法 之 “河”
算法结构
古典概型
随机数
伪随机数
几何概型
均匀随机数
二项分布
将学知识
已学知识
本节知识
教学评价
教学过程
教法手段
重点难点
教学目标
教材分析
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
教材分析
教学目标
重点难点
教法手段
教学过程
教学评价
随机数、伪随机数
为什么……
蒙特卡罗方法
算法的思想
(整数值)随机数和伪随机数是“桥”,而算法意义下的蒙特卡罗方法是“河”.
“桥”
“河”
教材目标
教材分析
重点难点
教法手段
教学过程
教学评价
(1)明确(整数值)随机数及伪随机数的概念;
(2)会用信息技术工具产生(整数值)随机数(实际上是伪随机数);
(3)通过具体案例理解蒙特卡罗方法(随机模拟方法),能针对具体的随机事件设计概率模型,并通过蒙特卡罗方法得出随机事件的概率的估计值.
(4)在信息技术环境下,通过算法解决大量重复模拟试验中的数据统计问题,实现计算随机事件的概率的估计值,并由此进一步体会算法思想与随机模拟方法.
重点难点
教学目标
教材分析
教法手段
教学过程
教学评价
教学重点
通过具体案例理解蒙特卡罗方法,并用算法的思想实现计算随机事件的概率的估计值这个过程.
重点难点
教学目标
教材分析
教法手段
教学过程
教学评价
教学难点
对于很难列举全部基本事件的古典概型或非古典概型中的随机事件(如概率为40%的下雨事件),建立什么样的概率模型来模拟,通过怎样的步骤来进行随机模拟试验,这是本节课的教学难点之一.
重点难点
教学目标
教材分析
教法手段
教学过程
教学评价
教学难点
如何通过算法使学生更好地体会蒙特卡罗方法是本节课的教学难点之二.
教法手段
教学目标
重点难点
教材分析
教学过程
教学评价
教师启发下的学生自主探究
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
以问题为主线,以学生为主体,以探究为途径,借助于信息技术,将数学的知识之“桥”与思想之“河”紧密地结合在一起.
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题1】天气预报说,在今后的三天中,每一天下雨的概率均为40%,这三天中恰有两天下雨的概率是多少?
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
一方面,是使学生从“每一天下雨的概率均为40%”认识到非古典概型的客观存在性,同时感受到这不是一个用已经学过的知识就能解决的问题,为引入随机数及蒙特卡罗方法作铺垫;
另一方面,使学生明确本节课的主要问题的同时,激发学生的学习欲望,使整个教学过程都围绕这个问题展开.
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题2】将一个骰子掷1次,向上一面出现1点的概率是多少?如果将一个骰子掷1000次,向上一面出现1点的次数大约是多少?如果通过试验的方法,要估计(掷一个骰子1次)向上一面出现1点的概率,你会怎么做?
(1) 引导学生复习古典概型;
(2)体会用试验方法求出随机事件出现的频率,并以此来估计概率的方法,
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题2】将一个骰子掷1次,向上一面出现1点的概率是多少?如果将一个骰子掷1000次,向上一面出现1点的次数大约是多少?如果通过试验的方法,要估计(掷一个骰子1次)向上一面出现1点的概率,你会怎么做?
(3)认识到人工试验耗时费事,并由此引出随机数的概念,介绍用计算器产生伪随机数的方法. 能用算法思想处理问题,为解决【问题1 】服务.
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
开始
输入试验次数n
j=1; m=0
j<=n
x=rand(6)+1
x=1
m=m+1
j=j+1
输出m/n
结束
Y
N
Y
N
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题3】在一个盒子中装有形状大小完全一样,但分别标有 0,1,2,3,4,5,6,7,8,9的十个球.(1)从盒子中随机摸一球,球上所标的数字是什么?
(2)从盒子中随机摸一球,球上所标的数字不超过3的概率是多少?
(3)如何用计算器产生随机数去估计(2)中的概率,具体步骤怎样?
让学生经历用蒙特卡罗方法来估计古典概型中随机事件的概率的过程,体会在算法思想指导下,用蒙特卡罗方法计算概率估计值的重要意义.
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题3】在一个盒子中装有形状大小完全一样,但分别标有 0,1,2,3,4,5,6,7,8,9的十个球.
(1)从盒子中随机摸一球,球上所标的数字是什么?
(2)从盒子中随机摸一球,球上所标的数字不超过3的概率是多少?
(3)如何用计算器产生随机数去估计(2)中的概率,具体步骤怎样?
学生认识到从盒子中随机摸一球,球上所标的数字是随机数.
概率为40%,与问题1中的“下雨概率为40%”对应
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
开始
输入试验次数n
j=1; m=0
j<=n
x=rand(10)
x≤3
m=m+1
j=j+1
输出m/n
结束
Y
N
Y
N
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题4】问题1中的“每一天下雨的概率均为40%”是不好试验的,但由问题3我们知道“从标有0,1,2,3,4,5,6,7,8,9的十个球中随机摸出一球,球上所标的数字不超过3的概率也是40%”,这个属古典概型的摸球过程不仅可以试验,而且还可以通过计算器产生随机数来模拟试验.你能设计一个算法解决问题1吗?
使学生在解决前面问题的基础上,完整地体会蒙特卡罗方法,进一步体会算法思想的应用,彻底解决问题1.
设计意图
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
师生活动
(1)教师:如果从十个球中摸出一球,球上的数字是0,1,2,3中的任何一个就表示下雨,否则就表示不下雨.
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
392
师生活动
(2)教师:那么三天的天气情况怎么模拟呢?
是
a=0:k=1
x=RAND(10)
x≤3
k≤3
m=m+1
a=2
m=0
a=a+1
k=k+1
否
否
否
是
是
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
师生活动
(3)教师:我们如何用计算机模拟的办法(即 蒙特卡罗的方法)来估计”三天中恰有两天下雨”的概率呢
(4)给学生思考与探索时间,然后与学生一起写出程序框图:
是
否
是
输入试验次数n
m=0:j=1
开始
a=0:k=1
x=RAND(10)
x≤3
j≤n
k≤3
j=j+1
a=2
m=m+1
输出m/n
结束
a=a+1
k=k+1
否
否
否
是
是
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
师生活动
(5)学生根据框图编出程序,在计算器上运行程序得出概率的估计值.
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
师生活动
(6)重复运行上述程序,逐渐增大模拟试验的次数n,通过观察每次运行程序后所得结果,使学生认识到所求概率的估计值的近似程度是随着n的增大而提高的.
师生活动
(7)教师结合问题1的解决过程,介绍蒙特卡罗方法及其应用的广泛性.指出蒙特卡罗方法的基本原理、思想 以及基本步骤.
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题5】你能从用蒙特卡罗方法解决问题1的过程中,得出用于模拟的概率模型的基本特征吗?你是否可以建立另一个概率模型用于模拟问题1中的随机事件?
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
5
4
3
2
1
下雨
不下雨
教学过程
教学目标
重点难点
教法手段
教材分析
教学评价
【问题6】你能举出一个用蒙特卡罗方法解决实际问题的实例吗?由你的实例说明使用蒙特卡罗方法时应该注意哪些方面?
让学生认识到用于模拟的概率模型不是唯一的,并通过建立另一个概率模型用于模拟试验,进一步体会蒙特卡罗方法的作用.
开拓学生视野,体会思想方法,小结本课内容 .
设计意图
教学评价
教学目标
重点难点
教法手段
教材分析
教学过程
探究作业: (即【问题1】的扩展研究)
天气预报说,在今后的三天中,每一天下雨的概率均为40%,那么在这三天中,有几天下雨的可能性大一些呢?
巩固学生对蒙特卡罗方法和算法思想的理解,让学生体会随机模拟的优点,使学生头脑中的思想之“河”流经更多的知识之“桥”,并使这条河更清澈,更流畅,更致远,……
设计意图
《 (整数值)随机数(random numbers)的产生 》
