人教版九年级数学上册22.1.3二次函数y=ax2 b的图像与性质 课时过关练习(Word版含解析)
文档属性
| 名称 | 人教版九年级数学上册22.1.3二次函数y=ax2 b的图像与性质 课时过关练习(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 159.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 08:36:44 | ||
图片预览




文档简介
《二次函数y=ax2+k的图像与性质》课时过关练习
知识储备:
抛物线y=ax2+k的平移情况
抛物线y=ax2向上(下)平移|k|,就可得到二次函数y=ax2+k的图象:①当k>0时,向上平移;
②当k<0时,向下平移.
一.选择题.
1.抛物线y=2x2-4的顶点坐标是 ( )
A.(1,-2)
B.(0,-2)
C.(1,-3)
D.(0,-4)
2.
如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式( )
A.y=(x-1)2+2
B.y=(x+1)2+2
C.y=x2+1
D.y=x2+3
3.
二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是 ( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
4.
抛物线C1:y=x2+1与抛物线C2关于x轴对称,则抛物线C2的表达式为( )
A.y=-x2
B.y=-x2+1
C.y=x2-1
D.y=-x2-1
5.
在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
二.填空题.
1.
写出顶点坐标为(0,-2),开口方向与抛物线y=2x2的方向相反,形状相同的抛物线表达式为____________.
2.
将二次函数y=x2的图象沿x轴向左平移2个单位,则平移后的抛物线对应的二次函数的表达式为________.
3.
将抛物线y=3x2-1向上平移4个单位后,所得抛物线是________,当x=________时,该抛物线有最________(填“大”或“小”)值,是________.
4.
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B,C,则BC的长为________.
三.解答题.
1.
在同一直角坐标系中,函数y=-x2+2的图象与函数y=-x2的图象有什么关系?
2.
已知:二次函数y=ax2+k(a≠0)经过点A(2,3),B(-1,6).
求:(1)该函数的表达式.
(2)若点C(-3,m),D(n,5)也在函数的图象上,求m,n的值.
3.
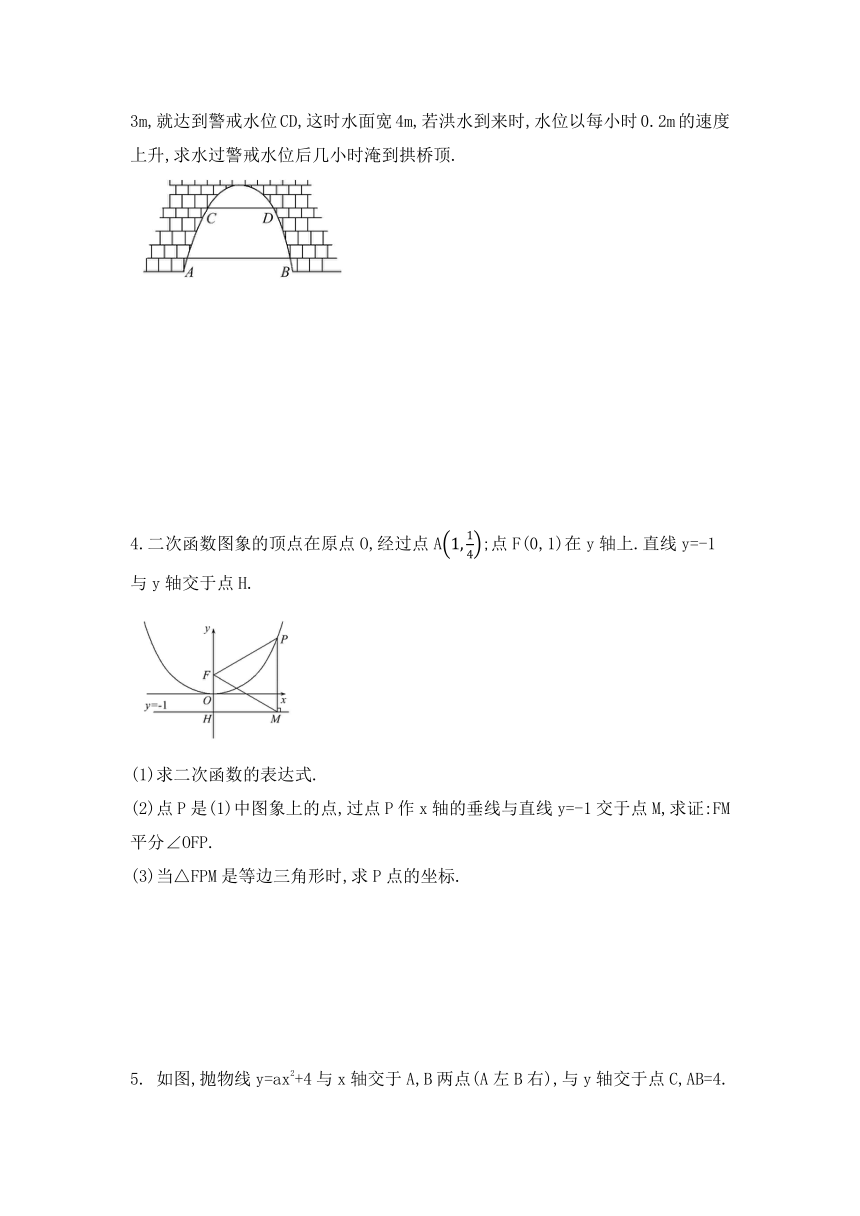
如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到拱桥顶.
4.二次函数图象的顶点在原点O,经过点A;点F(0,1)在y轴上.直线y=-1与y轴交于点H.
(1)求二次函数的表达式.
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP.
(3)当△FPM是等边三角形时,求P点的坐标.
5.
如图,抛物线y=ax2+4与x轴交于A,B两点(A左B右),与y轴交于点C,AB=4.
(1)求抛物线的表达式.
(2)若CD⊥AC,CD=AC,AD交抛物线于点P,求点P的坐标.
《二次函数y=ax2+k的图像与性质》课时过关练习(解析版)
知识储备:
抛物线y=ax2+k的平移情况
抛物线y=ax2向上(下)平移|k|,就可得到二次函数y=ax2+k的图象:①当k>0时,向上平移;
②当k<0时,向下平移.
一.选择题.
1.抛物线y=2x2-4的顶点坐标是 ( )
A.(1,-2)
B.(0,-2)
C.(1,-3)
D.(0,-4)
【解析】选D.y=ax2+k(a≠0)的顶点为(0,k),
∴y=2x2-4的顶点为(0,-4).
2.
如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是 ( )
A.y=(x-1)2+2
B.y=(x+1)2+2
C.y=x2+1
D.y=x2+3
【解析】选C.抛物线y=x2+2向下平移1个单位变为y=x2+2-1,即为y=x2+1.
3.
二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是 ( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
【解析】选D.A.a=2,则抛物线y=2x2-3的开口向上,所以A选项错误;B.当x=2时,y=2×4-3=5,则抛物线不经过点(2,3),所以B选项错误;C.抛物线的对称轴为直线x=0,所以C选项错误;D.当y=0时,2x2-3=0,此方程有两个不相等的实数解,所以D选项正确.
4.
抛物线C1:y=x2+1与抛物线C2关于x轴对称,则抛物线C2的表达式为( )
A.y=-x2
B.y=-x2+1
C.y=x2-1
D.y=-x2-1
【解析】选D.关于x轴对称的两个函数表达式的开口方向相反,开口大小相同,二次项的系数互为相反数;与y轴的交点互为相反数,那么常数项互为相反数.
5.
在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
【解析】选C.当a<0时,二次函数顶点在y轴负半轴,一次函数经过一、二、四象限;
当a>0时,二次函数顶点在y轴正半轴,一次函数经过一、二、三象限.
二.填空题.
1.
写出顶点坐标为(0,-2),开口方向与抛物线y=2x2的方向相反,形状相同的抛物线表达式为____________.
【解析】开口与y=2x2的方向相反,形状相同的抛物线的a的值为-2,又顶点为(0,-2).故所求的抛物线为y=-2x2-2.
答案:y=-2x2-2
2.
将二次函数y=x2的图象沿x轴向左平移2个单位,则平移后的抛物线对应的二次函数的表达式为________.
【解析】平移后二次函数解析式为:y=(x+2)2.
答案:y=(x+2)2
3.
将抛物线y=3x2-1向上平移4个单位后,所得抛物线是________,当x=________时,该抛物线有最________(填“大”或“小”)值,是________.
【解析】y=3x2-1+4得y=3x2+3.
当x=0时,y有最小值为3.
答案:y=3x2+3 0 小 3
4.
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B,C,则BC的长为________.
【解析】由题意知,A的坐标为(0,3),
∴直线BC可记为y=3,
当y=3时,x2=3,∴x=±3,
∴B(-3,3),C(3,3),∴BC=6.
答案:6.
三.解答题.
1.
在同一直角坐标系中,函数y=-x2+2的图象与函数y=-x2的图象有什么关系?
【解析】抛物线y=-x2+2与抛物线y=-x2的开口方向、开口大小、对称轴相同,但顶点坐标不同,函数y=-x2+2的图象可以看成将函数y=-x2的图象向上平移两个单位得到的.
2.
已知:二次函数y=ax2+k(a≠0)经过点A(2,3),B(-1,6).
求:(1)该函数的表达式.
(2)若点C(-3,m),D(n,5)也在函数的图象上,求m,n的值.
【解析】(1)∵y=ax2+k的图象经过点(2,3)和(-1,6),
∴∴∴y=-x2+7.
(2)当x=-3时y=-(-3)2+7=-2.即m=-2.
当y=5时,即-x2+7=5,∴x=±,即n=±.
3.
如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到拱桥顶.
【解析】根据题意建立坐标系如图:
设抛物线解析式为:y=ax2+h.
∵B(4,0),D(2,3),
∴解得:
∴y=-x2+4,∴M(0,4),即OM=4m,
∴MN=OM-ON=4-3=1,
则t==5(小时).
答:水过警戒水位后5小时淹到拱桥顶.
4.二次函数图象的顶点在原点O,经过点A;点F(0,1)在y轴上.直线y=-1与y轴交于点H.
(1)求二次函数的表达式.
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP.
(3)当△FPM是等边三角形时,求P点的坐标.
【解析】(1)∵二次函数图象的顶点在原点O,
∴设二次函数的表达式为y=ax2,
将点A代入y=ax2得:a=,
∴二次函数的表达式为y=x2.
(2)∵点P在抛物线y=x2上,
∴可设点P的坐标为,
过点P作PB⊥y轴于点B,则BF=,
PB=|x|,
∴在Rt△BPF中,
PF==x2+1,
∵PM⊥直线y=-1,∴PM=x2+1,
∴PF=PM,∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP.
(3)当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,∴x2+1=4,
解得:x=±2,
∴x2=4-1=3,
∴满足条件的点P的坐标为(2,3)或(-2,3).
5.
如图,抛物线y=ax2+4与x轴交于A,B两点(A左B右),与y轴交于点C,AB=4.
(1)求抛物线的表达式.
(2)若CD⊥AC,CD=AC,AD交抛物线于点P,求点P的坐标.
【解析】(1)抛物线y=ax2+4的对称轴为y轴.
∵与x轴交于A,B两点且AB=4,
∴点A的坐标为(-2,0),点B的坐标为(2,0),
将(2,0)代入表达式得0=4a+4.
解得a=-1,
∴抛物线的表达式为y=-x2+4.
(2)过点D作DE垂直于y轴,垂足为点E.
∵∠ACO+∠DCO=90°,∠DCE+∠CDE=90°,
∴∠ACO=∠CDE.
在△AOC和△CED中,∠AOC=∠CED,∠OCA=∠CDE,AC=CD,
∴△AOC≌△CED,
∴CO=ED=4,CE=AO=2,
∴点D(4,2).将A(-2,0),D(4,2)代入y=kx+b得
解得
∴AP所在直线表达式为y=x+,
将两函数联立得
解得或(舍去)
所以点P的坐标为.
知识储备:
抛物线y=ax2+k的平移情况
抛物线y=ax2向上(下)平移|k|,就可得到二次函数y=ax2+k的图象:①当k>0时,向上平移;
②当k<0时,向下平移.
一.选择题.
1.抛物线y=2x2-4的顶点坐标是 ( )
A.(1,-2)
B.(0,-2)
C.(1,-3)
D.(0,-4)
2.
如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式( )
A.y=(x-1)2+2
B.y=(x+1)2+2
C.y=x2+1
D.y=x2+3
3.
二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是 ( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
4.
抛物线C1:y=x2+1与抛物线C2关于x轴对称,则抛物线C2的表达式为( )
A.y=-x2
B.y=-x2+1
C.y=x2-1
D.y=-x2-1
5.
在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
二.填空题.
1.
写出顶点坐标为(0,-2),开口方向与抛物线y=2x2的方向相反,形状相同的抛物线表达式为____________.
2.
将二次函数y=x2的图象沿x轴向左平移2个单位,则平移后的抛物线对应的二次函数的表达式为________.
3.
将抛物线y=3x2-1向上平移4个单位后,所得抛物线是________,当x=________时,该抛物线有最________(填“大”或“小”)值,是________.
4.
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B,C,则BC的长为________.
三.解答题.
1.
在同一直角坐标系中,函数y=-x2+2的图象与函数y=-x2的图象有什么关系?
2.
已知:二次函数y=ax2+k(a≠0)经过点A(2,3),B(-1,6).
求:(1)该函数的表达式.
(2)若点C(-3,m),D(n,5)也在函数的图象上,求m,n的值.
3.
如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到拱桥顶.
4.二次函数图象的顶点在原点O,经过点A;点F(0,1)在y轴上.直线y=-1与y轴交于点H.
(1)求二次函数的表达式.
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP.
(3)当△FPM是等边三角形时,求P点的坐标.
5.
如图,抛物线y=ax2+4与x轴交于A,B两点(A左B右),与y轴交于点C,AB=4.
(1)求抛物线的表达式.
(2)若CD⊥AC,CD=AC,AD交抛物线于点P,求点P的坐标.
《二次函数y=ax2+k的图像与性质》课时过关练习(解析版)
知识储备:
抛物线y=ax2+k的平移情况
抛物线y=ax2向上(下)平移|k|,就可得到二次函数y=ax2+k的图象:①当k>0时,向上平移;
②当k<0时,向下平移.
一.选择题.
1.抛物线y=2x2-4的顶点坐标是 ( )
A.(1,-2)
B.(0,-2)
C.(1,-3)
D.(0,-4)
【解析】选D.y=ax2+k(a≠0)的顶点为(0,k),
∴y=2x2-4的顶点为(0,-4).
2.
如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是 ( )
A.y=(x-1)2+2
B.y=(x+1)2+2
C.y=x2+1
D.y=x2+3
【解析】选C.抛物线y=x2+2向下平移1个单位变为y=x2+2-1,即为y=x2+1.
3.
二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是 ( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
【解析】选D.A.a=2,则抛物线y=2x2-3的开口向上,所以A选项错误;B.当x=2时,y=2×4-3=5,则抛物线不经过点(2,3),所以B选项错误;C.抛物线的对称轴为直线x=0,所以C选项错误;D.当y=0时,2x2-3=0,此方程有两个不相等的实数解,所以D选项正确.
4.
抛物线C1:y=x2+1与抛物线C2关于x轴对称,则抛物线C2的表达式为( )
A.y=-x2
B.y=-x2+1
C.y=x2-1
D.y=-x2-1
【解析】选D.关于x轴对称的两个函数表达式的开口方向相反,开口大小相同,二次项的系数互为相反数;与y轴的交点互为相反数,那么常数项互为相反数.
5.
在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
【解析】选C.当a<0时,二次函数顶点在y轴负半轴,一次函数经过一、二、四象限;
当a>0时,二次函数顶点在y轴正半轴,一次函数经过一、二、三象限.
二.填空题.
1.
写出顶点坐标为(0,-2),开口方向与抛物线y=2x2的方向相反,形状相同的抛物线表达式为____________.
【解析】开口与y=2x2的方向相反,形状相同的抛物线的a的值为-2,又顶点为(0,-2).故所求的抛物线为y=-2x2-2.
答案:y=-2x2-2
2.
将二次函数y=x2的图象沿x轴向左平移2个单位,则平移后的抛物线对应的二次函数的表达式为________.
【解析】平移后二次函数解析式为:y=(x+2)2.
答案:y=(x+2)2
3.
将抛物线y=3x2-1向上平移4个单位后,所得抛物线是________,当x=________时,该抛物线有最________(填“大”或“小”)值,是________.
【解析】y=3x2-1+4得y=3x2+3.
当x=0时,y有最小值为3.
答案:y=3x2+3 0 小 3
4.
如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B,C,则BC的长为________.
【解析】由题意知,A的坐标为(0,3),
∴直线BC可记为y=3,
当y=3时,x2=3,∴x=±3,
∴B(-3,3),C(3,3),∴BC=6.
答案:6.
三.解答题.
1.
在同一直角坐标系中,函数y=-x2+2的图象与函数y=-x2的图象有什么关系?
【解析】抛物线y=-x2+2与抛物线y=-x2的开口方向、开口大小、对称轴相同,但顶点坐标不同,函数y=-x2+2的图象可以看成将函数y=-x2的图象向上平移两个单位得到的.
2.
已知:二次函数y=ax2+k(a≠0)经过点A(2,3),B(-1,6).
求:(1)该函数的表达式.
(2)若点C(-3,m),D(n,5)也在函数的图象上,求m,n的值.
【解析】(1)∵y=ax2+k的图象经过点(2,3)和(-1,6),
∴∴∴y=-x2+7.
(2)当x=-3时y=-(-3)2+7=-2.即m=-2.
当y=5时,即-x2+7=5,∴x=±,即n=±.
3.
如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到拱桥顶.
【解析】根据题意建立坐标系如图:
设抛物线解析式为:y=ax2+h.
∵B(4,0),D(2,3),
∴解得:
∴y=-x2+4,∴M(0,4),即OM=4m,
∴MN=OM-ON=4-3=1,
则t==5(小时).
答:水过警戒水位后5小时淹到拱桥顶.
4.二次函数图象的顶点在原点O,经过点A;点F(0,1)在y轴上.直线y=-1与y轴交于点H.
(1)求二次函数的表达式.
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP.
(3)当△FPM是等边三角形时,求P点的坐标.
【解析】(1)∵二次函数图象的顶点在原点O,
∴设二次函数的表达式为y=ax2,
将点A代入y=ax2得:a=,
∴二次函数的表达式为y=x2.
(2)∵点P在抛物线y=x2上,
∴可设点P的坐标为,
过点P作PB⊥y轴于点B,则BF=,
PB=|x|,
∴在Rt△BPF中,
PF==x2+1,
∵PM⊥直线y=-1,∴PM=x2+1,
∴PF=PM,∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP.
(3)当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,∴x2+1=4,
解得:x=±2,
∴x2=4-1=3,
∴满足条件的点P的坐标为(2,3)或(-2,3).
5.
如图,抛物线y=ax2+4与x轴交于A,B两点(A左B右),与y轴交于点C,AB=4.
(1)求抛物线的表达式.
(2)若CD⊥AC,CD=AC,AD交抛物线于点P,求点P的坐标.
【解析】(1)抛物线y=ax2+4的对称轴为y轴.
∵与x轴交于A,B两点且AB=4,
∴点A的坐标为(-2,0),点B的坐标为(2,0),
将(2,0)代入表达式得0=4a+4.
解得a=-1,
∴抛物线的表达式为y=-x2+4.
(2)过点D作DE垂直于y轴,垂足为点E.
∵∠ACO+∠DCO=90°,∠DCE+∠CDE=90°,
∴∠ACO=∠CDE.
在△AOC和△CED中,∠AOC=∠CED,∠OCA=∠CDE,AC=CD,
∴△AOC≌△CED,
∴CO=ED=4,CE=AO=2,
∴点D(4,2).将A(-2,0),D(4,2)代入y=kx+b得
解得
∴AP所在直线表达式为y=x+,
将两函数联立得
解得或(舍去)
所以点P的坐标为.
同课章节目录
