必修1 第一章 运动的描述 6. 匀变速直线运动位移与时间的关系 课件20张PPT
文档属性
| 名称 | 必修1 第一章 运动的描述 6. 匀变速直线运动位移与时间的关系 课件20张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览




文档简介
§2.6 匀变速直线运动的位移与时间的关系
预习案订正
学习目标
1. 了解“微元”法的基本思想。
2. 在“ v-t ”图象中,会用“面积”法求位移。
3. 掌握匀变速直线运动的位移公式,会用公式分析计算有关问题。
4. 会用“ x-t ”图象,分析物体的运动。
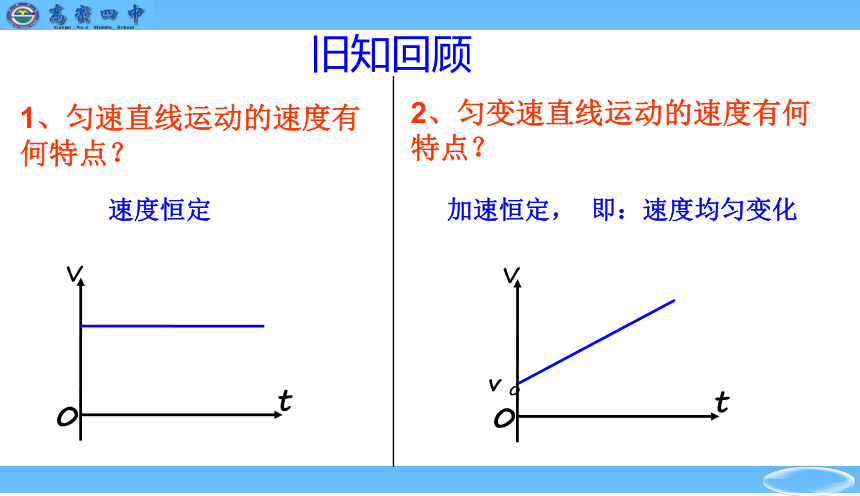
2、匀变速直线运动的速度有何特点?
旧知回顾
1、匀速直线运动的速度有何特点?
0
V
t
速度恒定
加速恒定, 即:速度均匀变化
0
V
t
v 0
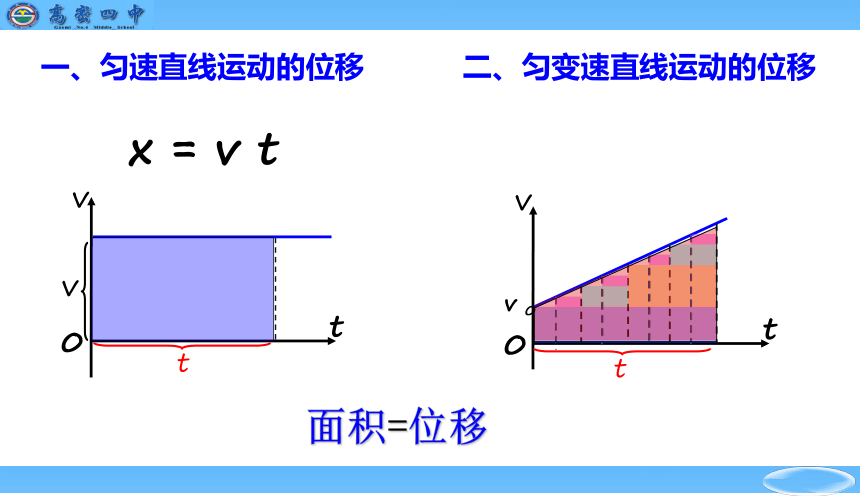
二、匀变速直线运动的位移
一、匀速直线运动的位移
0
V
t
V
t
x = v t
0
V
t
v 0
t
面积=位移
v
t
t
V0
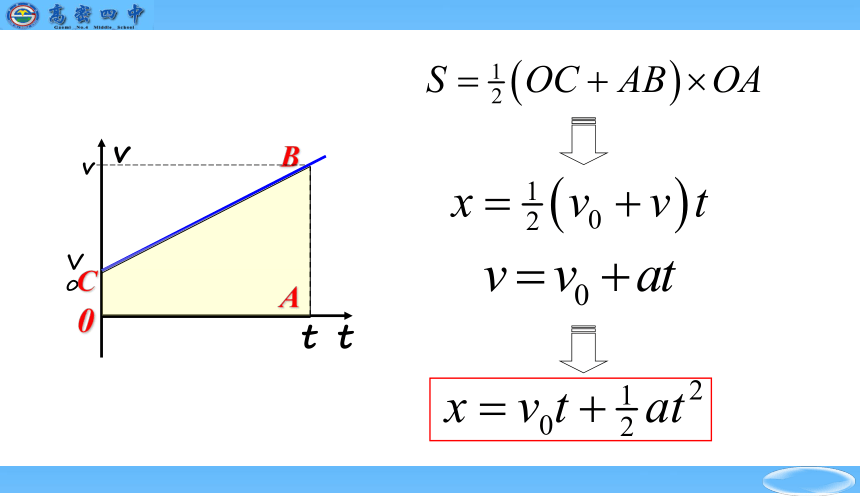
A
B
C
0
v
例1:一辆汽车以1m/s2的加速度加速行驶了12s,驶过了180m.汽车开始加速时的速度是多少?
解:规定汽车运动方向为正方向.
初速度为v0,a=1m/s2,t=12s,位移x=180m。
由 得:
位移公式的应用步骤
①确定一个方向为正方向(一般以初速度的方向为正方向)。
②根据规定的正方向确定已知量的正、负,并用带有正、负的数值表示。
③根据位移时间关系式或其变形式列式、求解。
④根据计算结果说明所求量的大小、方向。
例2:某一做直线运动的物体的v-t图像如图所示.根据图像求:
(1)物体距出发点的最远距离
(2)前4s内物体的位移
(3)前4s内通过的路程
位移在 v-t 图象中的表示
t 轴上方的面积,正方向位移
t 轴下方的面积,负方向位移
跟踪训练2.某军事试验场正在平地上试射地对空导弹,若某次竖直向上发射导弹时发生故障,造成导弹的v-t图象如图所示,则下述说法中正确的是( )
A.0~1 s内导弹匀速上升
B.1~2 s内导弹静止不动
C.3 s末导弹回到出发点
D.5 s末导弹恰好回到出发点
三、位移—时间图象(x-t图象)
坐标:某时刻所处的位置或相对于坐标原点的位移。
斜率:表示物体的速度。
例3.一列火车沿直线轨道运动,如图描述了它关于出发点的位移随时间变化的情况.通过分析回答以下问题:
(1)火车最远距离出发点多少米?
(2)试分析火车各阶段的运动状态.
跟踪训练3:如图是一辆汽车做直线运动的x-t图象,对线段OA、AB、BC、CD所表示的运动,下列说法正确的是( )
A.OA段运动速度最大
B.AB段物体做匀速运动
C.CD段的运动方向与初始运动方向相反
D.运动4 h汽车的位移大小为30 km
小 结
1、匀变速直线运动的位移
2、v-t 图像和 x-t 图像
坐标:某时刻的速度
斜率:加速度
面积:位移
坐标:某时刻相对原点的位移
斜率:速度
预习案订正
学习目标
1. 了解“微元”法的基本思想。
2. 在“ v-t ”图象中,会用“面积”法求位移。
3. 掌握匀变速直线运动的位移公式,会用公式分析计算有关问题。
4. 会用“ x-t ”图象,分析物体的运动。
2、匀变速直线运动的速度有何特点?
旧知回顾
1、匀速直线运动的速度有何特点?
0
V
t
速度恒定
加速恒定, 即:速度均匀变化
0
V
t
v 0
二、匀变速直线运动的位移
一、匀速直线运动的位移
0
V
t
V
t
x = v t
0
V
t
v 0
t
面积=位移
v
t
t
V0
A
B
C
0
v
例1:一辆汽车以1m/s2的加速度加速行驶了12s,驶过了180m.汽车开始加速时的速度是多少?
解:规定汽车运动方向为正方向.
初速度为v0,a=1m/s2,t=12s,位移x=180m。
由 得:
位移公式的应用步骤
①确定一个方向为正方向(一般以初速度的方向为正方向)。
②根据规定的正方向确定已知量的正、负,并用带有正、负的数值表示。
③根据位移时间关系式或其变形式列式、求解。
④根据计算结果说明所求量的大小、方向。
例2:某一做直线运动的物体的v-t图像如图所示.根据图像求:
(1)物体距出发点的最远距离
(2)前4s内物体的位移
(3)前4s内通过的路程
位移在 v-t 图象中的表示
t 轴上方的面积,正方向位移
t 轴下方的面积,负方向位移
跟踪训练2.某军事试验场正在平地上试射地对空导弹,若某次竖直向上发射导弹时发生故障,造成导弹的v-t图象如图所示,则下述说法中正确的是( )
A.0~1 s内导弹匀速上升
B.1~2 s内导弹静止不动
C.3 s末导弹回到出发点
D.5 s末导弹恰好回到出发点
三、位移—时间图象(x-t图象)
坐标:某时刻所处的位置或相对于坐标原点的位移。
斜率:表示物体的速度。
例3.一列火车沿直线轨道运动,如图描述了它关于出发点的位移随时间变化的情况.通过分析回答以下问题:
(1)火车最远距离出发点多少米?
(2)试分析火车各阶段的运动状态.
跟踪训练3:如图是一辆汽车做直线运动的x-t图象,对线段OA、AB、BC、CD所表示的运动,下列说法正确的是( )
A.OA段运动速度最大
B.AB段物体做匀速运动
C.CD段的运动方向与初始运动方向相反
D.运动4 h汽车的位移大小为30 km
小 结
1、匀变速直线运动的位移
2、v-t 图像和 x-t 图像
坐标:某时刻的速度
斜率:加速度
面积:位移
坐标:某时刻相对原点的位移
斜率:速度
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
