必修1_8. 匀变速直线运动规律的应用课件36张PPT
文档属性
| 名称 | 必修1_8. 匀变速直线运动规律的应用课件36张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览










文档简介
第一章 运动的描述 匀变速直线运动
第2讲 匀变速直线运动的规律
一、匀变速直线运动的规律
1.匀变速直线运动
沿一条直线且 不变的运动.
2.匀变速直线运动的基本规律
(1)速度公式: vt = .
(2)位移公式:x= .
(3)位移速度关系式: .
加速度
v0+at
vt 2-v02=2ax
自测1 (2018·山西省重点中学协作体期末)如图1所示,一小球从A点由静止开始沿斜面向下做匀变速直线运动,若到达B点时速度为vt ,到达C点时速度为
2vt ,则AB∶BC等于
A.1∶1 B.1∶2
C.1∶3 D.1∶4
图1
解析 根据匀变速直线运动的速度位移公式vt2-v02=2ax知,
√
所以AB∶AC=1∶4,则AB∶BC=1∶3,故C正确,A、B、D错误.
二、匀变速直线运动的推论
1.三个推论
(1)连续相等的相邻时间间隔T内的位移差相等,
即x2-x1=x3-x2=…=xn-xn-1= .
(2)做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初、末时刻速度矢量和的 ,还等于中间时刻的瞬时速度.
一半
aT2
2.初速度为零的匀加速直线运动的四个重要推论
(1)T末、2T末、3T末、…、nT末的瞬时速度之比为v1∶v2∶v3∶…∶vn= .
(2)前T内、前2T内、前3T内、…、前nT内的位移之比为x1∶x2∶x3∶…∶xn= .
(3)第1个T内、第2个T内、第3个T内、…、第n个T内的位移之比为xⅠ∶xⅡ∶xⅢ∶…∶xN= .
(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶tn
= .
1∶2∶3∶…∶n
12∶22∶32∶…∶n2
1∶3∶5∶…∶(2n-1)
自测2 (2018·河南省新乡市第三次模拟)汽车以某一初速度开始做匀加速直线运动,第1 s内行驶了1 m,第2 s内行驶了2 m,则汽车第3 s内的平均速度为
A.2 m/s B.3 m/s
C.4 m/s D.5 m/s
解析 根据匀变速直线运动的推论可知:x2-x1=x3-x2,则x3=3 m,
√
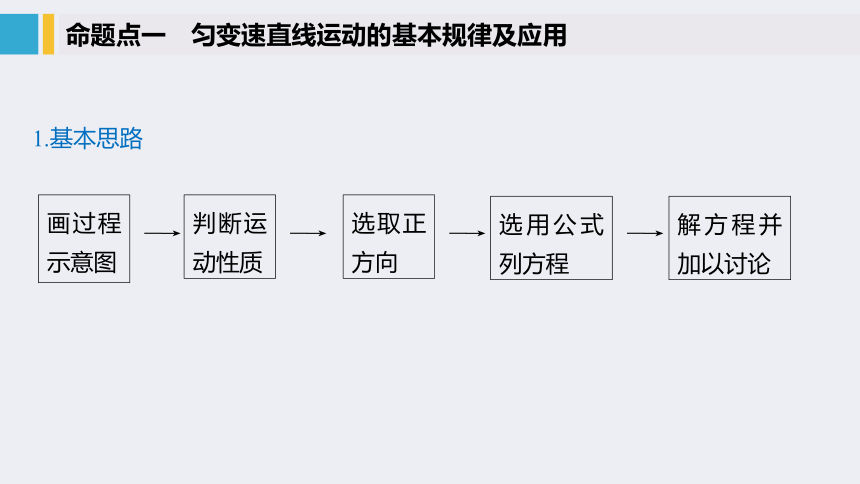
1.基本思路
命题点一 匀变速直线运动的基本规律及应用
画过程示意图
―→
判断运动性质
―→
选取正方向
―→
选用公式列方程
―→
解方程并加以讨论
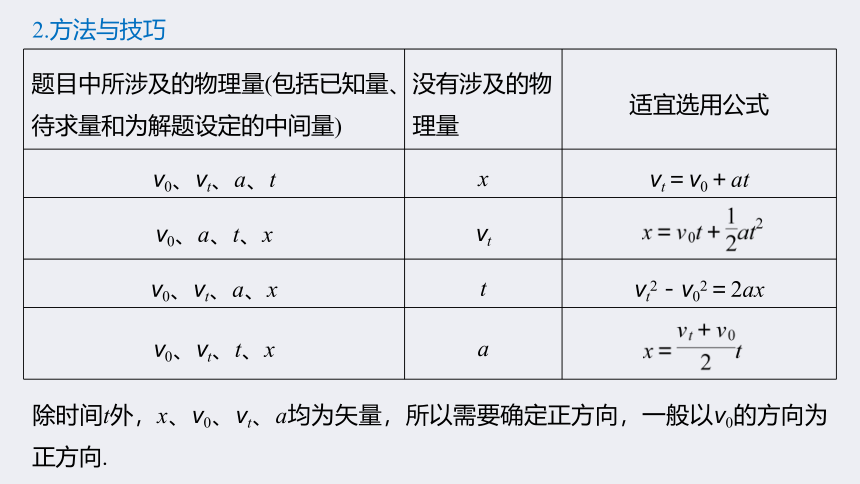
2.方法与技巧
题目中所涉及的物理量(包括已知量、待求量和为解题设定的中间量)
没有涉及的物理量
适宜选用公式
v0、vt、a、t
x
vt=v0+at
v0、a、t、x
vt
v0、vt、a、x
t
vt2-v02=2ax
v0、vt、t、x
a
除时间t外,x、v0、vt、a均为矢量,所以需要确定正方向,一般以v0的方向为正方向.
例1 (2018·湖南省永州市三模)质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位制单位),下列说法正确的是
A.该质点的加速度大小为1 m/s2
B.该质点在1 s末的速度大小为6 m/s
C.该质点第2 s内的平均速度为8 m/s
D.前2 s内的位移为8 m
√
所以该质点在1 s末的速度大小为v1=v0+at1=7 m/s,A、B错误;
该质点在前2 s内的位移为x1=5×2 m+22 m=14 m,
该质点在第1 s内的位移为x2=5×1 m+12 m=6 m,
变式1 (多选)(2019·河南省洛阳市调研)如图2所示,在一平直公路上,一辆汽车从O点由静止开始做匀加速直线运动,已知在3 s内经过相距30 m的A、B两点,汽车经过B点时的速度为15 m/s,则
A.汽车经过A点的速度大小为5 m/s
B.A点与O点间的距离为20 m
C.汽车从O点到A点需要的时间为5 s
D.汽车从O点到B点的平均速度大小为7.5 m/s
图2
√
√
由匀变速直线运动规律有vA2=2axOA,代入数据解得xOA=3.75 m,选项B错误;
由vA=atOA解得汽车从O点到A点需要的时间为tOA=1.5 s,选项C错误;
刹车类问题的处理技巧
拓展点
——逆向思维法的应用
刹车类问题:指匀减速到速度为零后立即停止运动,加速度a突然消失的问题,求解时要注意确定其实际运动时间.如果问题涉及最后阶段(到停止)的运动,可把该阶段看成反向的初速度为零、加速度不变的匀加速直线运动.
例2 (2018·山东省济南一中阶段检测)汽车在平直的公路上行驶,发现险情紧急刹车,汽车立即做匀减速直线运动直到停车,已知汽车刹车时第一秒内的位移为13 m,在最后1秒内的位移为2 m,则下列说法正确的是
A.汽车在第1秒末的速度可能为10 m/s
B.汽车加速度大小可能为3 m/s2
C.汽车在第1秒末的速度一定为11 m/s
D.汽车的加速度大小一定为4.5 m/s2
√
解析 采用逆向思维,由于最后1 s内的位移为2 m,
代入数据解得初速度v0=15 m/s,
则汽车在第1 s末的速度v1=v0-at=15 m/s-4×1 m/s=11 m/s,故C正确,A、B、D错误.
变式题:一物体以某一初速度在粗糙水平面上做匀减速直线运动,最后停下来,若此物体在最初5 s内和最后5 s经过的路程之比为11:5.则此物体一共运动了多长时间?
方法与技巧
命题点二 匀变速直线运动的推论及应用
例3 (2018·山东省日照市校际联合质检)一物体做匀加速直线运动,通过一段位移Δx所用时间为2t,紧接着通过下一段位移Δx所用时间为t.则物体运动的加速度大小为
类型1 平均速度公式的应用
√
变式2 (2018·江西省六校第五次联考)如图3所示,一小球(可视为质点)沿斜面匀加速下滑,依次经过A、B、C三点.已知AB=18 m,BC=30 m,小球经过AB和BC两段所用的时间均为2 s,则小球经过A、B、C三点时的速度大小分别是
A.12 m/s,13 m/s,14 m/s
B.10 m/s,14 m/s,18 m/s
C.8 m/s,10 m/s,16 m/s
D.6 m/s,12 m/s,18 m/s
图3
√
经过B点的瞬时速度等于通过AC段的平均速度,
则经过C点的速度vC=vB+at=12 m/s+3×2 m/s=18 m/s,经过A点的速度vA=vB-at=12 m/s-3×2 m/s=6 m/s,故D正确.
例4 (多选)(2019·甘肃省天水市质检)如图4所示,一冰壶以速度v垂直进入三个完全相同的矩形区域做匀减速直线运动,且刚要离开第三个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是
A.v1∶v2∶v3=3∶2∶1
图4
√
√
类型2 逆向思维法和初速度为零的匀变速直线运动推论的应用
解析 因为冰壶做匀减速直线运动,且末速度为零,故可以看成反向匀加速直线运动来研究.
变式3 (多选)一物块以一定的初速度从光滑斜面底端a点上滑,最高可滑至b点,后又滑回至a点,c是ab的中点,如图5所示,已知物块从a上滑至b所用时间为t,下列分析正确的是
A.物块从c运动到b所用的时间等于从b运动到c所用的时间
B.物块上滑过程的加速度与下滑过程的加速度等大反向
C.物块下滑时从b运动至c所用时间为 t
D.物块上滑通过c点时的速度大小等于整个上滑过程中平均速度的大小
√
图5
√
解析 由于斜面光滑,物块沿斜面向上与向下运动的加速度大小相同,a=gsin θ,故物块从c运动到b所用的时间等于从b运动到c所用的时间,选项A正确,B错误;
物块由b到a的过程是初速度为零的匀加速直线运动,
由于c是位移的中点,物块上滑过程中通过c点的速度不等于整个上滑过程的平均速度,选项D错误.
1.(2018·福建省漳州市期末调研)如图1为伽利略研究自由落体运动规律时设计的斜面实验.他让铜球在阻力很小的斜面上从静止滚下,利用滴水计时记录铜球运动的时间.关于伽利略的“斜面实验”,下列说法正
确的是
A.在倾角较小的斜面上进行实验,可“冲淡”重力
的作用,使测量时间更容易
B.伽利略通过对自由落体运动的研究,进行合理外
推得出铜球在斜面做匀变速运动
C.若斜面倾角一定,不同质量的铜球在斜面上运动时速度变化的快慢不同
D.若斜面倾角一定,铜球沿斜面运动的位移与所用时间成正比
双基巩固练
√
图1
1
2
3
4
5
6
7
解析 自由落体运动下落很快,不易计时,伽利略让小球沿阻力很小的斜面滚下,延长了小球的运动时间,“冲淡”了重力的作用,故A正确;
伽利略在研究物体变速运动规律时,做了著名的“斜面实验”,他测量了铜球在较小倾角斜面上的运动情况,发现铜球做的是匀变速直线运动,且铜球加速度随斜面倾角的增大而增大,于是他对更大倾角的情况进行了合理的外推,由此得出的结论是自由落体运动是一种匀变速直线运动,故B错误;
小球沿斜面下滑,做匀加速直线运动,由于阻力很小,可忽略不计,由mgsin θ=ma可知,加速度a=gsin θ,所以斜面倾角一定,加速度与质量无关,质量不同的小球加速度都相同,故C错误;
若斜面倾角一定,加速度a=gsin θ一定,铜球沿斜面运动的位移x= at2,与所用时间平方成正比,故D错误.
1
2
3
4
5
6
7
2.(2018·天津市南开中学月考)汽车以20 m/s的速度在平直公路上行驶,急刹车时的加速度大小为5 m/s2,则自驾驶员急踩刹车开始,经过2 s与5 s汽车的位移之比为
A.5∶4 B.4∶5 C.3∶4 D.4∶3
所以2 s与5 s汽车的位移之比为3∶4,故选项C正确.
√
1
2
3
4
5
6
7
3.(2019·广东省韶关市质检)物体由静止开始做匀加速直线运动,加速8 s后,立即做匀减速直线运动,再经过4 s停下.关于该物体的运动情况,下列说法正确的是
A.加速、减速过程中的加速度大小之比为2∶1
B.加速、减速过程中的平均速度大小之比为2∶1
C.加速、减速过程中的位移大小之比为2∶1
D.加速、减速过程中速度的变化率大小之比为2∶1
√
1
2
3
4
5
6
7
解析 设匀加速直线运动的末速度大小为vt,
可知a1∶a2=t2∶t1=1∶2,则速度变化率大小之比为1∶2,故A、D错误;
根据匀变速直线运动的平均速度推论知,
即平均速度大小之比为1∶1,故B错误;
1
2
3
4
5
6
7
4.(2018·广东省汕头市第二次模拟)如图2,一骑行者所骑自行车前后轮轴的距离为L,在水平道路上匀速运动,当看到道路前方有一条减速带时,立刻刹车使自行车做减速直线运动,自行车垂直经过该减速带时,前、后轮造成的两次颠簸的时间间隔为t.利用以上数据,可以求出前、后轮经过减速带这段时间内自行车的
A.初速度 B.末速度
C.平均速度 D.加速度
√
图2
1
2
3
4
5
6
7
解析 自行车垂直经过该减速带时,前、后轮造成的两次颠簸的时间间隔为t,自行车前后轮轴的距离为L,只知道两个物理量,所以不能求出vt、v0、a三个物理量,故A、B、D错误;
由平均速度定义可得: 能求出平均速度,故C正确.
1
2
3
4
5
6
7
5.(2018·安徽省滁州市联合质检)将一个小球从报废的矿井口由静止释放后做自由落体运动,4 s末落到井底.该小球开始下落后第2 s内和第4 s内的平均速度之比是
A.1∶3 B.2∶4
C.3∶7 D.1∶4
√
1
2
3
4
5
6
7
解析 根据公式vt=gt可得,第1 s末小球的速度为v1=g,第2 s末小球的速度为v2=2g,
第3 s末小球的速度为v3=3g,第4 s末小球的速度为v4=4g,
1
2
3
4
5
6
7
6.(2018·陕西省宝鸡市质检二)一个小球由静止开始沿斜面下滑,经3 s进入一个水平面,再经6 s停下,斜面与水平面交接处的能量损失不计,则小球在斜面上和水平面上运动的位移大小之比是
A.1∶1 B.1∶2 C.1∶3 D.2∶1
√
1
2
3
4
5
6
7
7.(2018·河南省南阳信阳等六市二模)假设某次海试活动中,“蛟龙号”完成海底任务后竖直上浮,从上浮速度为v时开始计时,此后“蛟龙号”匀减速上浮,经过时间t上浮到海面,速度恰好减为零,则“蛟龙号”在t0(t0√
根据逆向思维,可知“蛟龙号”在t0时刻距离海平面的深度为:
1
2
3
4
5
6
7
第2讲 匀变速直线运动的规律
一、匀变速直线运动的规律
1.匀变速直线运动
沿一条直线且 不变的运动.
2.匀变速直线运动的基本规律
(1)速度公式: vt = .
(2)位移公式:x= .
(3)位移速度关系式: .
加速度
v0+at
vt 2-v02=2ax
自测1 (2018·山西省重点中学协作体期末)如图1所示,一小球从A点由静止开始沿斜面向下做匀变速直线运动,若到达B点时速度为vt ,到达C点时速度为
2vt ,则AB∶BC等于
A.1∶1 B.1∶2
C.1∶3 D.1∶4
图1
解析 根据匀变速直线运动的速度位移公式vt2-v02=2ax知,
√
所以AB∶AC=1∶4,则AB∶BC=1∶3,故C正确,A、B、D错误.
二、匀变速直线运动的推论
1.三个推论
(1)连续相等的相邻时间间隔T内的位移差相等,
即x2-x1=x3-x2=…=xn-xn-1= .
(2)做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初、末时刻速度矢量和的 ,还等于中间时刻的瞬时速度.
一半
aT2
2.初速度为零的匀加速直线运动的四个重要推论
(1)T末、2T末、3T末、…、nT末的瞬时速度之比为v1∶v2∶v3∶…∶vn= .
(2)前T内、前2T内、前3T内、…、前nT内的位移之比为x1∶x2∶x3∶…∶xn= .
(3)第1个T内、第2个T内、第3个T内、…、第n个T内的位移之比为xⅠ∶xⅡ∶xⅢ∶…∶xN= .
(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶tn
= .
1∶2∶3∶…∶n
12∶22∶32∶…∶n2
1∶3∶5∶…∶(2n-1)
自测2 (2018·河南省新乡市第三次模拟)汽车以某一初速度开始做匀加速直线运动,第1 s内行驶了1 m,第2 s内行驶了2 m,则汽车第3 s内的平均速度为
A.2 m/s B.3 m/s
C.4 m/s D.5 m/s
解析 根据匀变速直线运动的推论可知:x2-x1=x3-x2,则x3=3 m,
√
1.基本思路
命题点一 匀变速直线运动的基本规律及应用
画过程示意图
―→
判断运动性质
―→
选取正方向
―→
选用公式列方程
―→
解方程并加以讨论
2.方法与技巧
题目中所涉及的物理量(包括已知量、待求量和为解题设定的中间量)
没有涉及的物理量
适宜选用公式
v0、vt、a、t
x
vt=v0+at
v0、a、t、x
vt
v0、vt、a、x
t
vt2-v02=2ax
v0、vt、t、x
a
除时间t外,x、v0、vt、a均为矢量,所以需要确定正方向,一般以v0的方向为正方向.
例1 (2018·湖南省永州市三模)质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位制单位),下列说法正确的是
A.该质点的加速度大小为1 m/s2
B.该质点在1 s末的速度大小为6 m/s
C.该质点第2 s内的平均速度为8 m/s
D.前2 s内的位移为8 m
√
所以该质点在1 s末的速度大小为v1=v0+at1=7 m/s,A、B错误;
该质点在前2 s内的位移为x1=5×2 m+22 m=14 m,
该质点在第1 s内的位移为x2=5×1 m+12 m=6 m,
变式1 (多选)(2019·河南省洛阳市调研)如图2所示,在一平直公路上,一辆汽车从O点由静止开始做匀加速直线运动,已知在3 s内经过相距30 m的A、B两点,汽车经过B点时的速度为15 m/s,则
A.汽车经过A点的速度大小为5 m/s
B.A点与O点间的距离为20 m
C.汽车从O点到A点需要的时间为5 s
D.汽车从O点到B点的平均速度大小为7.5 m/s
图2
√
√
由匀变速直线运动规律有vA2=2axOA,代入数据解得xOA=3.75 m,选项B错误;
由vA=atOA解得汽车从O点到A点需要的时间为tOA=1.5 s,选项C错误;
刹车类问题的处理技巧
拓展点
——逆向思维法的应用
刹车类问题:指匀减速到速度为零后立即停止运动,加速度a突然消失的问题,求解时要注意确定其实际运动时间.如果问题涉及最后阶段(到停止)的运动,可把该阶段看成反向的初速度为零、加速度不变的匀加速直线运动.
例2 (2018·山东省济南一中阶段检测)汽车在平直的公路上行驶,发现险情紧急刹车,汽车立即做匀减速直线运动直到停车,已知汽车刹车时第一秒内的位移为13 m,在最后1秒内的位移为2 m,则下列说法正确的是
A.汽车在第1秒末的速度可能为10 m/s
B.汽车加速度大小可能为3 m/s2
C.汽车在第1秒末的速度一定为11 m/s
D.汽车的加速度大小一定为4.5 m/s2
√
解析 采用逆向思维,由于最后1 s内的位移为2 m,
代入数据解得初速度v0=15 m/s,
则汽车在第1 s末的速度v1=v0-at=15 m/s-4×1 m/s=11 m/s,故C正确,A、B、D错误.
变式题:一物体以某一初速度在粗糙水平面上做匀减速直线运动,最后停下来,若此物体在最初5 s内和最后5 s经过的路程之比为11:5.则此物体一共运动了多长时间?
方法与技巧
命题点二 匀变速直线运动的推论及应用
例3 (2018·山东省日照市校际联合质检)一物体做匀加速直线运动,通过一段位移Δx所用时间为2t,紧接着通过下一段位移Δx所用时间为t.则物体运动的加速度大小为
类型1 平均速度公式的应用
√
变式2 (2018·江西省六校第五次联考)如图3所示,一小球(可视为质点)沿斜面匀加速下滑,依次经过A、B、C三点.已知AB=18 m,BC=30 m,小球经过AB和BC两段所用的时间均为2 s,则小球经过A、B、C三点时的速度大小分别是
A.12 m/s,13 m/s,14 m/s
B.10 m/s,14 m/s,18 m/s
C.8 m/s,10 m/s,16 m/s
D.6 m/s,12 m/s,18 m/s
图3
√
经过B点的瞬时速度等于通过AC段的平均速度,
则经过C点的速度vC=vB+at=12 m/s+3×2 m/s=18 m/s,经过A点的速度vA=vB-at=12 m/s-3×2 m/s=6 m/s,故D正确.
例4 (多选)(2019·甘肃省天水市质检)如图4所示,一冰壶以速度v垂直进入三个完全相同的矩形区域做匀减速直线运动,且刚要离开第三个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是
A.v1∶v2∶v3=3∶2∶1
图4
√
√
类型2 逆向思维法和初速度为零的匀变速直线运动推论的应用
解析 因为冰壶做匀减速直线运动,且末速度为零,故可以看成反向匀加速直线运动来研究.
变式3 (多选)一物块以一定的初速度从光滑斜面底端a点上滑,最高可滑至b点,后又滑回至a点,c是ab的中点,如图5所示,已知物块从a上滑至b所用时间为t,下列分析正确的是
A.物块从c运动到b所用的时间等于从b运动到c所用的时间
B.物块上滑过程的加速度与下滑过程的加速度等大反向
C.物块下滑时从b运动至c所用时间为 t
D.物块上滑通过c点时的速度大小等于整个上滑过程中平均速度的大小
√
图5
√
解析 由于斜面光滑,物块沿斜面向上与向下运动的加速度大小相同,a=gsin θ,故物块从c运动到b所用的时间等于从b运动到c所用的时间,选项A正确,B错误;
物块由b到a的过程是初速度为零的匀加速直线运动,
由于c是位移的中点,物块上滑过程中通过c点的速度不等于整个上滑过程的平均速度,选项D错误.
1.(2018·福建省漳州市期末调研)如图1为伽利略研究自由落体运动规律时设计的斜面实验.他让铜球在阻力很小的斜面上从静止滚下,利用滴水计时记录铜球运动的时间.关于伽利略的“斜面实验”,下列说法正
确的是
A.在倾角较小的斜面上进行实验,可“冲淡”重力
的作用,使测量时间更容易
B.伽利略通过对自由落体运动的研究,进行合理外
推得出铜球在斜面做匀变速运动
C.若斜面倾角一定,不同质量的铜球在斜面上运动时速度变化的快慢不同
D.若斜面倾角一定,铜球沿斜面运动的位移与所用时间成正比
双基巩固练
√
图1
1
2
3
4
5
6
7
解析 自由落体运动下落很快,不易计时,伽利略让小球沿阻力很小的斜面滚下,延长了小球的运动时间,“冲淡”了重力的作用,故A正确;
伽利略在研究物体变速运动规律时,做了著名的“斜面实验”,他测量了铜球在较小倾角斜面上的运动情况,发现铜球做的是匀变速直线运动,且铜球加速度随斜面倾角的增大而增大,于是他对更大倾角的情况进行了合理的外推,由此得出的结论是自由落体运动是一种匀变速直线运动,故B错误;
小球沿斜面下滑,做匀加速直线运动,由于阻力很小,可忽略不计,由mgsin θ=ma可知,加速度a=gsin θ,所以斜面倾角一定,加速度与质量无关,质量不同的小球加速度都相同,故C错误;
若斜面倾角一定,加速度a=gsin θ一定,铜球沿斜面运动的位移x= at2,与所用时间平方成正比,故D错误.
1
2
3
4
5
6
7
2.(2018·天津市南开中学月考)汽车以20 m/s的速度在平直公路上行驶,急刹车时的加速度大小为5 m/s2,则自驾驶员急踩刹车开始,经过2 s与5 s汽车的位移之比为
A.5∶4 B.4∶5 C.3∶4 D.4∶3
所以2 s与5 s汽车的位移之比为3∶4,故选项C正确.
√
1
2
3
4
5
6
7
3.(2019·广东省韶关市质检)物体由静止开始做匀加速直线运动,加速8 s后,立即做匀减速直线运动,再经过4 s停下.关于该物体的运动情况,下列说法正确的是
A.加速、减速过程中的加速度大小之比为2∶1
B.加速、减速过程中的平均速度大小之比为2∶1
C.加速、减速过程中的位移大小之比为2∶1
D.加速、减速过程中速度的变化率大小之比为2∶1
√
1
2
3
4
5
6
7
解析 设匀加速直线运动的末速度大小为vt,
可知a1∶a2=t2∶t1=1∶2,则速度变化率大小之比为1∶2,故A、D错误;
根据匀变速直线运动的平均速度推论知,
即平均速度大小之比为1∶1,故B错误;
1
2
3
4
5
6
7
4.(2018·广东省汕头市第二次模拟)如图2,一骑行者所骑自行车前后轮轴的距离为L,在水平道路上匀速运动,当看到道路前方有一条减速带时,立刻刹车使自行车做减速直线运动,自行车垂直经过该减速带时,前、后轮造成的两次颠簸的时间间隔为t.利用以上数据,可以求出前、后轮经过减速带这段时间内自行车的
A.初速度 B.末速度
C.平均速度 D.加速度
√
图2
1
2
3
4
5
6
7
解析 自行车垂直经过该减速带时,前、后轮造成的两次颠簸的时间间隔为t,自行车前后轮轴的距离为L,只知道两个物理量,所以不能求出vt、v0、a三个物理量,故A、B、D错误;
由平均速度定义可得: 能求出平均速度,故C正确.
1
2
3
4
5
6
7
5.(2018·安徽省滁州市联合质检)将一个小球从报废的矿井口由静止释放后做自由落体运动,4 s末落到井底.该小球开始下落后第2 s内和第4 s内的平均速度之比是
A.1∶3 B.2∶4
C.3∶7 D.1∶4
√
1
2
3
4
5
6
7
解析 根据公式vt=gt可得,第1 s末小球的速度为v1=g,第2 s末小球的速度为v2=2g,
第3 s末小球的速度为v3=3g,第4 s末小球的速度为v4=4g,
1
2
3
4
5
6
7
6.(2018·陕西省宝鸡市质检二)一个小球由静止开始沿斜面下滑,经3 s进入一个水平面,再经6 s停下,斜面与水平面交接处的能量损失不计,则小球在斜面上和水平面上运动的位移大小之比是
A.1∶1 B.1∶2 C.1∶3 D.2∶1
√
1
2
3
4
5
6
7
7.(2018·河南省南阳信阳等六市二模)假设某次海试活动中,“蛟龙号”完成海底任务后竖直上浮,从上浮速度为v时开始计时,此后“蛟龙号”匀减速上浮,经过时间t上浮到海面,速度恰好减为零,则“蛟龙号”在t0(t0
根据逆向思维,可知“蛟龙号”在t0时刻距离海平面的深度为:
1
2
3
4
5
6
7
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
