必修1_5. 匀变速直线运动速度与时间的关系课件31张PPT
文档属性
| 名称 | 必修1_5. 匀变速直线运动速度与时间的关系课件31张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 992.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 18:01:16 | ||
图片预览







文档简介
1.5 匀变速直线运动
速度与时间的关系
匀速直线速动
定义:物体在一条直线上运动,且在任意相等的时间间隔内的位移相等 。
t/s
v/(m./s)
0
v
2.2-1
特点:1、v-t图像是一条平行于时间轴的直线。
2、速度恒定,加速度为零。
*
1.从v-t图像中我们能得出哪些信息?
(1)质点在任一时刻的瞬时速度(大小和方向)及任一速度所对应的时刻;
(2)比较速度的变化快慢,即加速度
0
t
t1
t2
v
v0
v1
v2
v3
v4
t4
t3
△v
△v′
△t
△t′
=
△v
a = ——
△t
△v′
a′= ——
△t′
一、匀变速直线运动
1、定义:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动(uniform variable rectilinear motion)。匀变速直线运动的v-t图象是一条倾斜的直线。
2、在匀变速直线运动中,如果物体的速度随时间均匀增加,这个运动叫做匀加速直线运动;如果物体的速度随时间均匀减小,这个运动叫做匀减速直线运动。
匀变速直线运动
?t’
?v’
?t
?v
v
0
t1
t2
t3
t4
t
v4
v3
v2
v1
2.2-3
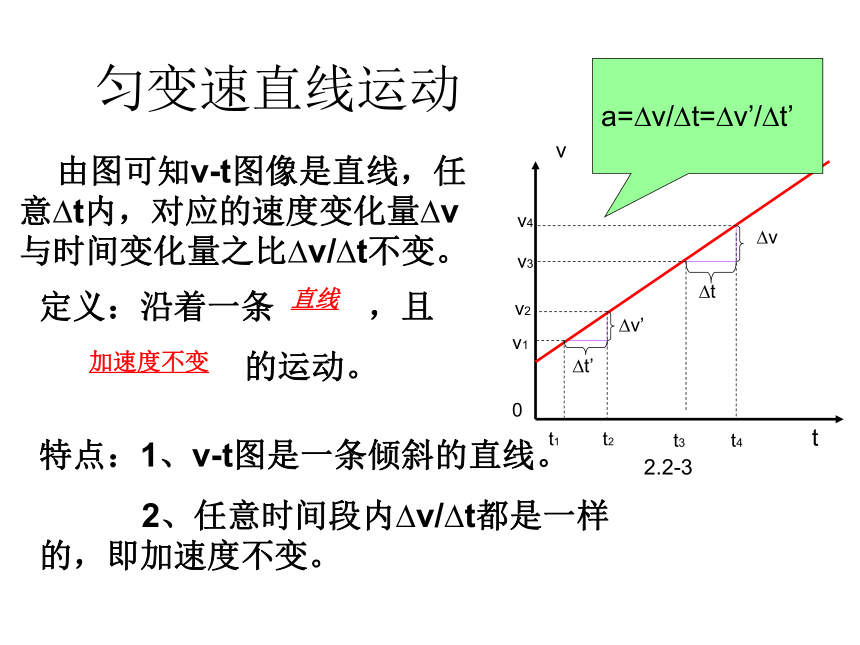
特点:1、v-t图是一条倾斜的直线。
2、任意时间段内?v/?t都是一样 的,即加速度不变。
由图可知v-t图像是直线,任意?t内,对应的速度变化量?v与时间变化量之比?v/?t不变。
定义:沿着一条 ,且
的运动。
直线
加速度不变
a=?v/?t=?v’/?t’
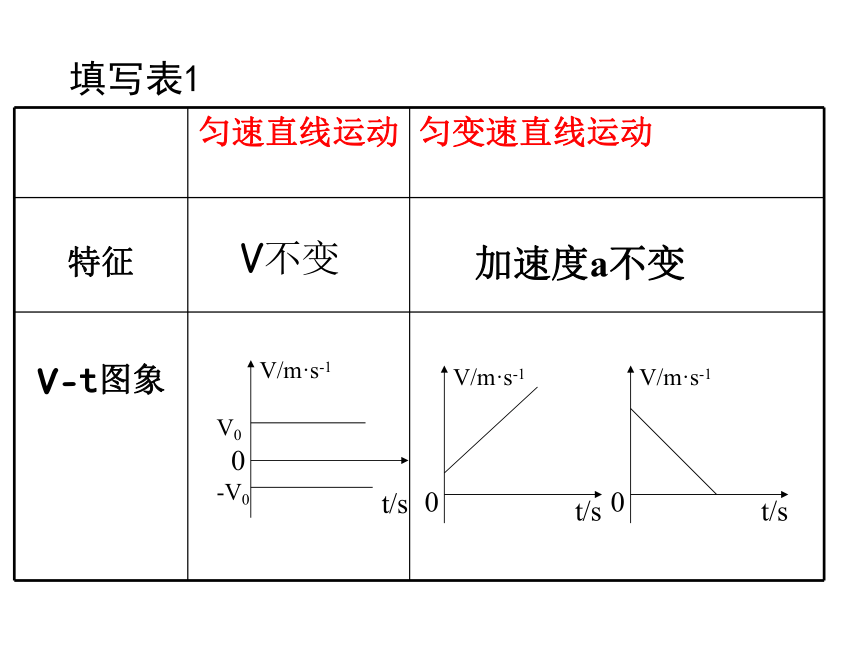
填写表1
匀速直线运动
匀变速直线运动
特征
V-t图象
V不变
加速度a不变
0
V/m·s-1
t/s
V0
-V0
V/m·s-1
t/s
0
V/m·s-1
t/s
0
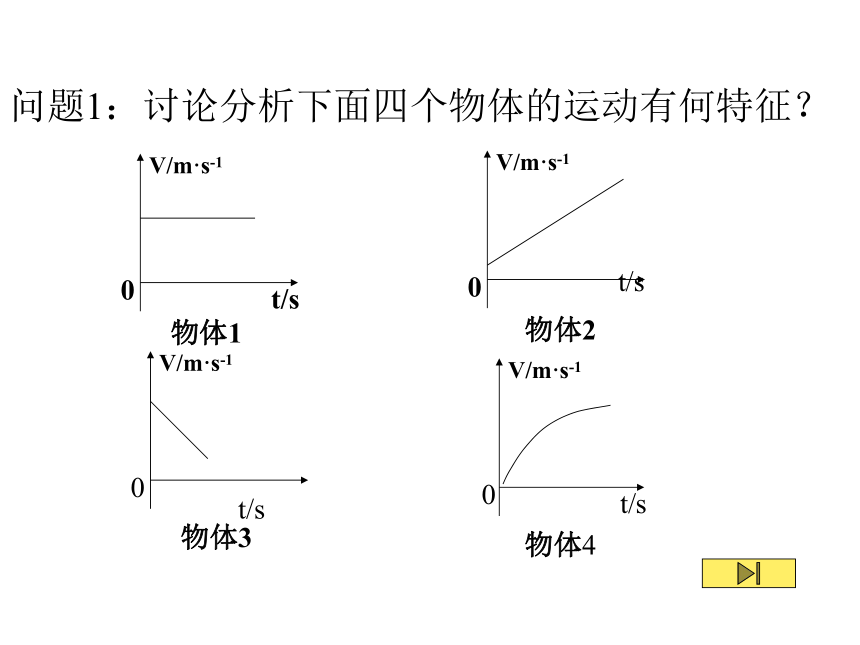
问题1:讨论分析下面四个物体的运动有何特征?
t/s
V/m·s-1
0
物体3
t/s
V/m·s-1
0
物体2
V/m·s-1
t/s
0
物体1
V/m·s-1
t/s
0
物体4
匀加速
t
v
0
v
匀减速
t
v
0
v
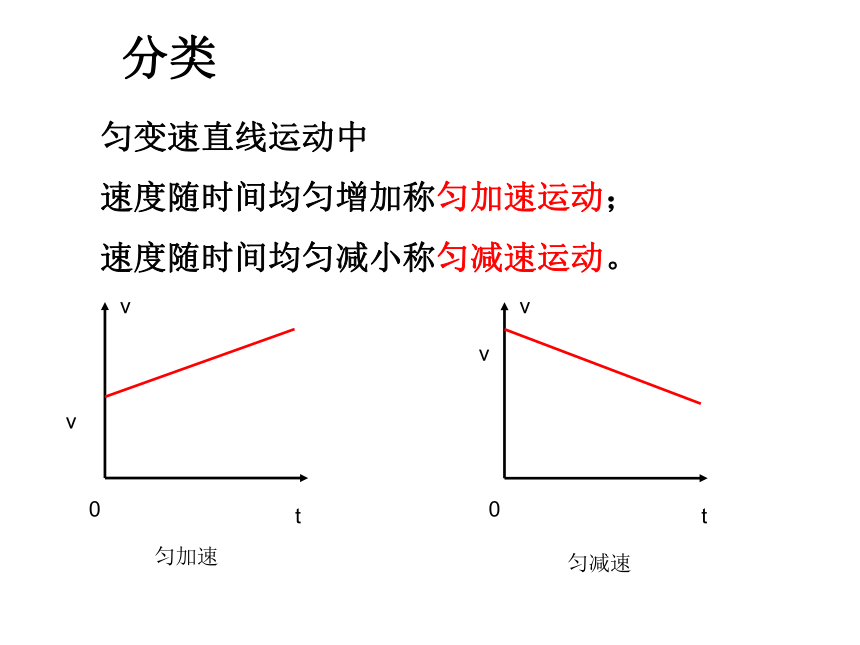
匀变速直线运动中
速度随时间均匀增加称匀加速运动;
速度随时间均匀减小称匀减速运动。
分类
*
v0 >0,a >0
v0 <0,a <0
匀加速
(a、v同向)
匀减速
(a、v反向)
v0 <0,a >0
v0 >0,a <0
匀加速
匀加速
匀减速
匀减速
b
v
0
t
t1
v
a
0
v
t
t1
v
t1
t2
t3
c
v
0
t
v1
v2
t4
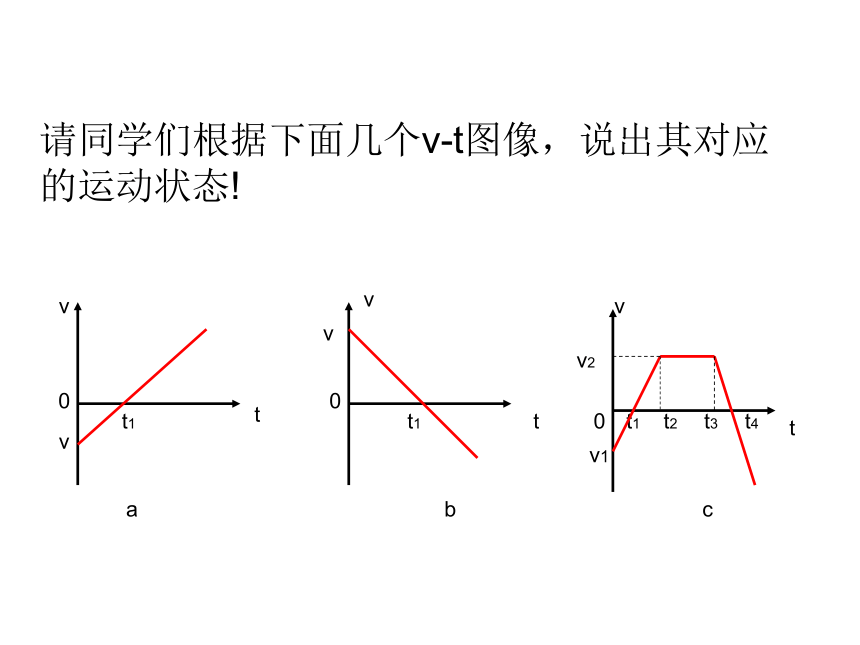
请同学们根据下面几个v-t图像,说出其对应的运动状态!
a图中0—t1时间段是初速度为v的负向匀减速直线运动;
t1时刻后,速度为0做反向(正向)匀加速运动。
b图中0—t1时间段是初速度为v的匀减速直线运动;
t1时刻后,以速度0做反向(负向)匀加速运动。
c图中0—t1时间段是初速度为v1的负向匀减速直线运动;
t1—t2时间段以速度0做反向(正向)匀加速运动至速度为v2;
t2—t3时间段做速度为v2的匀速运动;
t3—t4时间段是初速度为v2的匀减速直线运动;
t4时刻后,以速度0做反向(负向)匀加速运动。
答:
匀变速直线运动
2.分类:
(1)匀加速直线运动: 若物体的速度随时间均匀增加,称为匀加速直线运动,(a、v同向)如汽车起动、飞机起飞、石块自由下落等均可近似认为是匀加速直线运动。
(2)匀减速直线运动: 若物体的速度随时间均匀减少,称为匀减速直线运动,(a、v反向)如汽车刹车、飞机降落、石块被竖直向上抛等均可近似认为是匀减速直线运动。
二、匀变速直线运动的速度公式的推导
△t=t-0
△v=vt-v0
代入 a= △v/ △t,得:
变形,得: vt=v0+at
v0
t
v
t
v
0
Δv=at
v0
从图象上看V与t的关系如右图所示
V=at+V0
y=kx+b
vt=v0+at
o
v/m.s-1
t/s
v0
v
v0
Δv=at
t
三、速度与时间的关系
把运动开始(t=0)到任意t时刻时间间隔作为时间的变化量?t,t时刻的速度v与开始时刻的速度v0之差就是速度的变化量?v。
?t=t-0
?v=v-v0
v=v0+αt
解出:
因为?V/?t=α
末速度
初速度
加速度
运动时间
例题1、
例题1:汽车以40km/h的速度匀速行驶,现以0.6m/s2的加速度加速,10s后速度能达到多少?
初速度v0= 40km/h=11m/s 加速度α= 0.6m/s2 时间t=10s
v=v0+αt
=11m/s+ 0.6m/s2×10s
=17m/s=61km/h
答:10s后可达61km/h。
解:
解:加速度a=-6m/s2 时间t=2s
2s时的速度v=0
根据:V=v0+at我们有初速度
v0=V-at
=0-(-0.6m/s2)×2s
=12m/s
=43km/h
某汽车在某路面紧急刹车时,加速度的大小是6 m/s2,如果必须在2s内停下来,汽车的行驶速度最高不能超过多少?
例题2:
*
例3.某汽车正以12m/s的速度在路面上匀速行驶,前方出现紧急情况需刹车,加速度大小是3m/s2,求汽车5s末的速度。
解:以初速方向为正方向
则v=v0+at=12+(-3)×5m/s=-3m/s
正确解法:以初速方向为正方向
当车速减为零时,v=v0+at=12-3t=0
解得t=4s
即4s末汽车已刹车完毕,所以5s末时
汽车处于静止状态,即速度为零。
刹车问题
(与实际相符)
注意:
解题总结
解题步骤:
1、规定正方向(设初速度方向为正方向)加速运动,a为正值。减速运动,a为负值。
2、明确初速度v0、末速度v、加速度a和时间t及各量的正负号。
3、将已知量带入公式求未知量,若所求量是矢量,要说明方向。
归纳总结
从v-t图象中我们能得出哪些信息?
1、质点在任一时刻的瞬时速度及任一速
度所对应的时刻;
2、比较速度的变化快慢;
3、确定加速度的大小和方向 。
讨论与探究
1、描述各图线①②③表示的运动情况怎样?
o
v
t
1
2
3
t1
2、图象中图线的交点有什么意义?
讨论与探究
请叙述它的运动情况 ?
o
V/m.s-1
t/s
1
4
4
说一说
o
v
t
v1
v2
v3
v4
t1
t2
t3
t4
Δt’
Δt
Δv
Δv’
思考1:物体运动的速度怎样变化?
思考2:在相等的时间间隔内,速度的变化量总是相等吗?
思考3:物体在做匀加速运动吗?
四、速度与时间的关系式
V=v0+at
问
题
1、在公式中,各物理量的意义是什么 ?
2、在公式中,哪些物理量是矢量 ?
3、利用公式计算时,对于矢量怎么处理?
根据v-t图象判断物体的运动情况:
0
t
v
(B)
x
o
以v0速度做匀速直线
x
o
初速度为零的加速直线
0
t
v
(A)
v0
0
t
v
(C)
v0
0
t
v
(D)
v0
x
o
以初速度v0做加速直线
x
o
以初速度v0做减速直线
0
t
v
(E)
t0
-2
2
-1
1
t2
t1
0
t
v
(F)
2
-2
t0
t1
x
o
x
o
正方向减速
-2
0
负向减速
正方向加速
2
0
负方向加速
O
v/m·s-1
t/s
4
6
2
4
6
2
以初速度为正方向
1、前2秒内的加速度
2、2s—4s的加速度
0
3、4s—6s的加速度
注意:加速度为负值表示速度减小,此时,加速度方向与速度方向相反
0
t
v
某物体的v-t图象如下,问:
思考与讨论
1、此物体做匀加速直线运动吗?为什么?
t1
t2
2、请比较物体在t1和t2这两个时刻的加速度a1和a2的大小?
说一说
v
0
t1
t2
t3
t4
t
v4
v3
v2
v1
2.2-4
?t’
?v’
?v
?t
速度怎样变化?
速度均匀变化吗?
是匀加速吗?
速度与时间的关系
匀速直线速动
定义:物体在一条直线上运动,且在任意相等的时间间隔内的位移相等 。
t/s
v/(m./s)
0
v
2.2-1
特点:1、v-t图像是一条平行于时间轴的直线。
2、速度恒定,加速度为零。
*
1.从v-t图像中我们能得出哪些信息?
(1)质点在任一时刻的瞬时速度(大小和方向)及任一速度所对应的时刻;
(2)比较速度的变化快慢,即加速度
0
t
t1
t2
v
v0
v1
v2
v3
v4
t4
t3
△v
△v′
△t
△t′
=
△v
a = ——
△t
△v′
a′= ——
△t′
一、匀变速直线运动
1、定义:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动(uniform variable rectilinear motion)。匀变速直线运动的v-t图象是一条倾斜的直线。
2、在匀变速直线运动中,如果物体的速度随时间均匀增加,这个运动叫做匀加速直线运动;如果物体的速度随时间均匀减小,这个运动叫做匀减速直线运动。
匀变速直线运动
?t’
?v’
?t
?v
v
0
t1
t2
t3
t4
t
v4
v3
v2
v1
2.2-3
特点:1、v-t图是一条倾斜的直线。
2、任意时间段内?v/?t都是一样 的,即加速度不变。
由图可知v-t图像是直线,任意?t内,对应的速度变化量?v与时间变化量之比?v/?t不变。
定义:沿着一条 ,且
的运动。
直线
加速度不变
a=?v/?t=?v’/?t’
填写表1
匀速直线运动
匀变速直线运动
特征
V-t图象
V不变
加速度a不变
0
V/m·s-1
t/s
V0
-V0
V/m·s-1
t/s
0
V/m·s-1
t/s
0
问题1:讨论分析下面四个物体的运动有何特征?
t/s
V/m·s-1
0
物体3
t/s
V/m·s-1
0
物体2
V/m·s-1
t/s
0
物体1
V/m·s-1
t/s
0
物体4
匀加速
t
v
0
v
匀减速
t
v
0
v
匀变速直线运动中
速度随时间均匀增加称匀加速运动;
速度随时间均匀减小称匀减速运动。
分类
*
v0 >0,a >0
v0 <0,a <0
匀加速
(a、v同向)
匀减速
(a、v反向)
v0 <0,a >0
v0 >0,a <0
匀加速
匀加速
匀减速
匀减速
b
v
0
t
t1
v
a
0
v
t
t1
v
t1
t2
t3
c
v
0
t
v1
v2
t4
请同学们根据下面几个v-t图像,说出其对应的运动状态!
a图中0—t1时间段是初速度为v的负向匀减速直线运动;
t1时刻后,速度为0做反向(正向)匀加速运动。
b图中0—t1时间段是初速度为v的匀减速直线运动;
t1时刻后,以速度0做反向(负向)匀加速运动。
c图中0—t1时间段是初速度为v1的负向匀减速直线运动;
t1—t2时间段以速度0做反向(正向)匀加速运动至速度为v2;
t2—t3时间段做速度为v2的匀速运动;
t3—t4时间段是初速度为v2的匀减速直线运动;
t4时刻后,以速度0做反向(负向)匀加速运动。
答:
匀变速直线运动
2.分类:
(1)匀加速直线运动: 若物体的速度随时间均匀增加,称为匀加速直线运动,(a、v同向)如汽车起动、飞机起飞、石块自由下落等均可近似认为是匀加速直线运动。
(2)匀减速直线运动: 若物体的速度随时间均匀减少,称为匀减速直线运动,(a、v反向)如汽车刹车、飞机降落、石块被竖直向上抛等均可近似认为是匀减速直线运动。
二、匀变速直线运动的速度公式的推导
△t=t-0
△v=vt-v0
代入 a= △v/ △t,得:
变形,得: vt=v0+at
v0
t
v
t
v
0
Δv=at
v0
从图象上看V与t的关系如右图所示
V=at+V0
y=kx+b
vt=v0+at
o
v/m.s-1
t/s
v0
v
v0
Δv=at
t
三、速度与时间的关系
把运动开始(t=0)到任意t时刻时间间隔作为时间的变化量?t,t时刻的速度v与开始时刻的速度v0之差就是速度的变化量?v。
?t=t-0
?v=v-v0
v=v0+αt
解出:
因为?V/?t=α
末速度
初速度
加速度
运动时间
例题1、
例题1:汽车以40km/h的速度匀速行驶,现以0.6m/s2的加速度加速,10s后速度能达到多少?
初速度v0= 40km/h=11m/s 加速度α= 0.6m/s2 时间t=10s
v=v0+αt
=11m/s+ 0.6m/s2×10s
=17m/s=61km/h
答:10s后可达61km/h。
解:
解:加速度a=-6m/s2 时间t=2s
2s时的速度v=0
根据:V=v0+at我们有初速度
v0=V-at
=0-(-0.6m/s2)×2s
=12m/s
=43km/h
某汽车在某路面紧急刹车时,加速度的大小是6 m/s2,如果必须在2s内停下来,汽车的行驶速度最高不能超过多少?
例题2:
*
例3.某汽车正以12m/s的速度在路面上匀速行驶,前方出现紧急情况需刹车,加速度大小是3m/s2,求汽车5s末的速度。
解:以初速方向为正方向
则v=v0+at=12+(-3)×5m/s=-3m/s
正确解法:以初速方向为正方向
当车速减为零时,v=v0+at=12-3t=0
解得t=4s
即4s末汽车已刹车完毕,所以5s末时
汽车处于静止状态,即速度为零。
刹车问题
(与实际相符)
注意:
解题总结
解题步骤:
1、规定正方向(设初速度方向为正方向)加速运动,a为正值。减速运动,a为负值。
2、明确初速度v0、末速度v、加速度a和时间t及各量的正负号。
3、将已知量带入公式求未知量,若所求量是矢量,要说明方向。
归纳总结
从v-t图象中我们能得出哪些信息?
1、质点在任一时刻的瞬时速度及任一速
度所对应的时刻;
2、比较速度的变化快慢;
3、确定加速度的大小和方向 。
讨论与探究
1、描述各图线①②③表示的运动情况怎样?
o
v
t
1
2
3
t1
2、图象中图线的交点有什么意义?
讨论与探究
请叙述它的运动情况 ?
o
V/m.s-1
t/s
1
4
4
说一说
o
v
t
v1
v2
v3
v4
t1
t2
t3
t4
Δt’
Δt
Δv
Δv’
思考1:物体运动的速度怎样变化?
思考2:在相等的时间间隔内,速度的变化量总是相等吗?
思考3:物体在做匀加速运动吗?
四、速度与时间的关系式
V=v0+at
问
题
1、在公式中,各物理量的意义是什么 ?
2、在公式中,哪些物理量是矢量 ?
3、利用公式计算时,对于矢量怎么处理?
根据v-t图象判断物体的运动情况:
0
t
v
(B)
x
o
以v0速度做匀速直线
x
o
初速度为零的加速直线
0
t
v
(A)
v0
0
t
v
(C)
v0
0
t
v
(D)
v0
x
o
以初速度v0做加速直线
x
o
以初速度v0做减速直线
0
t
v
(E)
t0
-2
2
-1
1
t2
t1
0
t
v
(F)
2
-2
t0
t1
x
o
x
o
正方向减速
-2
0
负向减速
正方向加速
2
0
负方向加速
O
v/m·s-1
t/s
4
6
2
4
6
2
以初速度为正方向
1、前2秒内的加速度
2、2s—4s的加速度
0
3、4s—6s的加速度
注意:加速度为负值表示速度减小,此时,加速度方向与速度方向相反
0
t
v
某物体的v-t图象如下,问:
思考与讨论
1、此物体做匀加速直线运动吗?为什么?
t1
t2
2、请比较物体在t1和t2这两个时刻的加速度a1和a2的大小?
说一说
v
0
t1
t2
t3
t4
t
v4
v3
v2
v1
2.2-4
?t’
?v’
?v
?t
速度怎样变化?
速度均匀变化吗?
是匀加速吗?
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
