第29章 直线与圆的位置关系单元测试卷(含解析)
文档属性
| 名称 | 第29章 直线与圆的位置关系单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 14:14:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
冀教版九年级数学下册第29章 直线与圆的位置关系单元测试卷
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中,只有一项是符合题目要求的)
1.若☉O的半径为7cm,圆心O到直线l的距离为8cm,则直线l与☉O的位置关系是 ( )
A.相交 B.相切 C.相离 D.不确定
2.☉O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与☉O的位置关系是 ( )
A.点P在☉O内 B.点P的☉O上
C.点P在☉O外 D.点P在☉O上或☉O外
3.如图,在半径为2的☉O中,C为直径AB延长线上一点,CD与☉O相切于点D,连接AD,已知∠DAC=30°,则线段CD的长为 ( )
A.1 B. C.2 D.2
第3题图 第4题图
4.如图,AB是☉O的直径,点C为☉O外一点,CA,CD是☉O的切线,A,D为切点,连接BD,AD.若∠ACD=48°,则∠DBA的大小是 ( )
A.32° B.48° C.60° D.66°
5.如图,边长为a的正六边形内有两个三角形(数据如图),则= ( )
A.3 B.4 C.5 D.6
第5题图 第6题图
6.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,连接OC与半圆相交于点D,则CD的长为 ( )
A.1 B. C.2 D.2
7.在数轴上,点A所表示的实数为3,点B所表示的实数为a,☉A的半径为2.下列说法不正确的是 ( )
A.当a<5时,点B在☉A内 B.当1C.当a<1时,点B在☉A外 D.当a>5时,点B在☉A外
8.如图,△ABC是一张周长为17cm的三角形纸片,BC=5cm,☉O是它的内切圆,小明准备用剪刀在☉O的右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm B.7cm
C.6cm D.随直线MN的变化而变化
9.如图,已知P为☉O外一点,连接OP交☉O于点A,且OA=2AP,求作直线PB,使PB与☉O相切.以下是甲、乙两同学的作法.
甲:作OP的中垂线,交☉O于点B,则直线PB即所求.
乙:取OP的中点M,以M为圆心、OM长为半径画弧,交☉O于点B,则直线PB即所求.
对于两人的作法,下列说法正确的是 ( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
第9题图 第10题图
10.如图,等腰三角形ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也停止.设运动时间为t(s),以点O为圆心,OB长为半径的☉O与BA交于另一点E,连接ED.当直线DE与☉O相切时,t的取值是 ( )
A. B. C. D.
11.如图,圆内接正八边形的边长为1,以正八边形的一边AB作正方形ABCD,将正方形ABCD绕点B顺时针旋转,使BC与正八边形的另一边BC'重合,则正方形ABCD与正方形A'BC'D'重叠部分的面积为 ( )
A. B.-1 C. D.
第11题图 第12题图
12.如图,已知△ABC,以AB为直径的☉O交AC于点E,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下结论:①DF是☉O的切线;②CF=EF;③=.其中正确结论的序号是 ( )
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题共4小题,每小题3分,共12分)
13.如图,正八边形ABCDEFGH内接于☉O,点P是上的任意一点,则∠CPE的度数为 .?
第13题图 第14题图
14.如图,P是△ABC的内心,连接PA,PB,PC,△PAB,△PBC,△PAC的面积分别为S1,S2,S3.则S1 S2+S3.(填“<”“=”或“>”)?
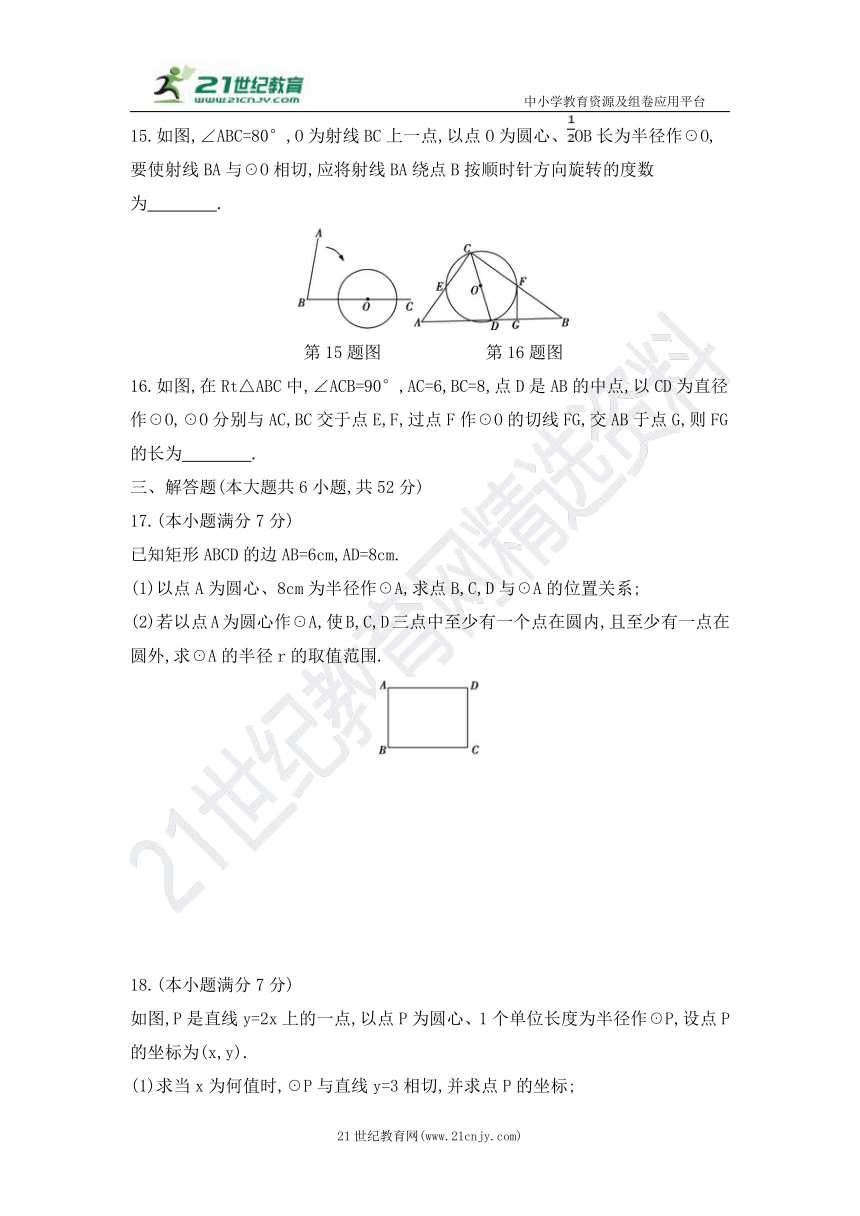
15.如图,∠ABC=80°,O为射线BC上一点,以点O为圆心、OB长为半径作☉O,要使射线BA与☉O相切,应将射线BA绕点B按顺时针方向旋转的度数为 .?
第15题图 第16题图
16.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作☉O,☉O分别与AC,BC交于点E,F,过点F作☉O的切线FG,交AB于点G,则FG的长为 .?
三、解答题(本大题共6小题,共52分)
17.(本小题满分7分)
已知矩形ABCD的边AB=6cm,AD=8cm.
(1)以点A为圆心、8cm为半径作☉A,求点B,C,D与☉A的位置关系;
(2)若以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,求☉A的半径r的取值范围.
18.(本小题满分7分)
如图,P是直线y=2x上的一点,以点P为圆心、1个单位长度为半径作☉P,设点P的坐标为(x,y).
(1)求当x为何值时,☉P与直线y=3相切,并求点P的坐标;
(2)直接写出当x为何值时,☉P与直线y=3相交、相离.
19.(本小题满分8分)
如图,在Rt△ABC中,∠C=90°,以BC为直径的☉O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.
20.(本小题满分8分)
已知☉O中,AC为直径,MA,MB分别切☉O于点A,B.
(1)如图1,若∠BAC=23°,求∠AMB的大小;
(2)如图2,过点B作BD∥MA,交AC于点E,交☉O于点D,若BD=MA,求∠AMB的大小.
21.(本小题满分10分)
如图,☉O的直径AB为10cm,弦BC为5cm,D,E分别是∠ACB的平分线与☉O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC,AD的长;
(2)试判断PC与☉O的位置关系,并说明理由.
22.(本小题满分12分)
如图1,在Rt△OGF中,∠GOF=90°,OF=2,∠GFO=30°.
(1)OG= ;?
(2)若☉O的半径为1,交直线OF于点C,点P是直线GF上的动点,PA,PB分别切☉O于点A,B.
①求PB的最小值;
②连接BC,AC,如图2所示,若∠BCA=54°,求∠APB的度数;
③在直线GF上是否存在点P,使得∠APB=60°?若存在,请求出FP的长;若不存在,请说明理由.
图1 图2
参 考 答 案 与 解 析
1.C 【解析】 ∵☉O的半径为7cm,圆心O到直线l的距离为8cm,7<8,∴直线l与☉O相离.故选C.
2.A 【解析】 ∵圆心O的坐标为(0,0),点P的坐标为(4,2),∴OP==<5,∴点P在☉O内.故选A.
3.D 【解析】 连接OD,∵OA=OD,∴∠OAD=∠ODA=30°.∵CD与☉O相切于点D,∴OD⊥CD.∵∠DOC=2∠DAC=2×30°=60°,∴∠C=30°,∴CD=OD=2.故选D.
4.D 【解析】 ∵CA,CD是☉O的切线,∴CA=CD.∵∠ACD=48°,∴∠CAD=∠CDA=66°.∵CA⊥AB,AB是直径,∴∠ADB=∠CAB=90°,∴∠DBA+∠DAB=90°,∠CAD+∠DAB=90°,∴∠DBA=∠CAD=66°,故选D.
5.C 【解析】 解法一 如图,设正六边形的中心为O.连接OA,OB.∵∠AOB=360°÷6=60°,OA=OB,∴△OAB是等边三角形,易知S正六边形=6S△OAB.∵图中的两个直角三角形可拼成一个边长为a的等边三角形,∴S空白=S△OAB,∴=====5.
解法二 通过割补题图可得如图所示的图形,所以=5.
6.C 【解析】 如图,设☉O与AC相切于点E,连接OE,则OE⊥AC,∵AB=10,AC=8,BC=6,∴AB2=AC2+BC2,∴∠ACB=90°,∴BC⊥AC,∴OE∥BC.由AO=OB=AB,易知OE=BC=3,∴OD=3.在Rt△ABC中,OC是斜边AB上的中线,∴OC=AB=5,∴CD=OC-OD=5-3=2.故选C.
7.A 【解析】 设点A,B之间的距离为d,由于圆心A在数轴上所表示的实数为3,圆的半径r=2,所以当d=r时,☉A与数轴交于两点,所表示的实数分别是1和5,故当a=1或a=5时,点B在☉A上;当dr,即当a<1或a>5时,点B在☉A外.由以上结论可知B项、C项、D项不符合题意,A项符合题意.故选A.
8.B 【解析】 如图,设D,E,F分别是☉O的切点,∵☉O是△ABC的内切圆,BC=5cm,∴BD+CE=BC=5cm,∵AB+BC+AC=17cm,∴AD+AE=7cm.∵DM=MF,FN=EN,∴AM+AN+MN=AD+AE=7cm.故选B.
9.D 【解析】 如图1,作OP的垂直平分线交OP于点H,连接OB,设AP=x,则OA=2x,OB=2x.∵BH垂直平分OP,∴BO=BP=2x.∵OB2+BP2=(2x)2+(2x)2=8x2,OP2=(3x)2=9x2,∴△OBP不是直角三角形,∴PB不是☉O的切线,∴甲的作法错误.如图2,连接OB,∵点M为OP的中点,∴OP为☉M的直径,∴∠OBP=90°,∴OB⊥PB,∴PB与☉O相切,∴乙的作法正确.故选D.
10.A 【解析】 如图,作AH⊥BC于H,依题意得BE=2tcm,BD=(8-2t)cm.∵AB=AC=5cm,BC=8cm,∴BH=CH=BC=4cm.当BE⊥DE时,直线DE与☉O相切,则∠BED=90°,又∵∠EBD=∠ABH,∴△BED∽△BHA,∴=,即=,解得t=.故选A.
11.B 【解析】 正八边形的内角∠ABC'==135°,正方形ABCD绕点B顺时针旋转,使BC与正八边形的另一边BC'重合,设CD与A'D'相交于点E,∴∠ABC=∠A'BC'=90°,∠BA'D'=∠BAD=90°,∴∠ABA'=135°-90°=45°.延长BA',则BA'过点D,如图,则∠A'DE=∠ABA'=∠A'ED=45°,∴A'E=A'D.∵AB=1,∴A'B=AB=1,BD=,∴A'E=A'D=-1,∴正方形ABCD与正方形A'BC'D'重叠部分的面积=S△BDC-S△DA'E=×1×1-×(-1)×(-1)=-1.故选B.
12.A 【解析】 如图,连接OD,DE,AD,∵DB=DC,∴OD是△ABC的中位线,∴OD∥AC.∵DF⊥AC,∴DF⊥OD,∴DF是☉O的切线,故①正确.∵∠CED+∠AED=180°,∠B+∠AED=180°,∴∠CED=∠B.∵AB是☉O的直径,∴∠ADB=90°,即AD⊥BC.∵BD=CD,∴AB=AC,∴∠B=∠C,∴∠CED=∠C,∴DC=DE.又∵DF⊥AC,∴CF=EF,故②正确.当∠EAD=∠EDA时,=,此时△ABC为等边三角形,当△ABC不是等边三角形时,∠EAD≠∠EDA,则≠,∴=不一定正确.综上,正确结论的序号是①②.故选A.
13.45° 【解析】 连接OD,OC,OE,∵八边形ABCDEFGH是正八边形,∴∠COD=∠DOE==45°,∴∠COE=45°+45°=90°,∴∠CPE=∠COE=45°.
14.< 【解析】 过点P作三边的垂线PD,PE,PF,根据点P是△ABC的内心,可得PD=PE=PF,设PD=PE=PF=h,则S1=AB·h,S2+S3=(AC+BC)·h,根据三角形的两边之和大于第三边,得S115.50°或110° 【解析】 如图,旋转后射线BA与☉O相切分两种情况,设旋转后与☉O相切于点D,E,连接OD,OE,∵OD=OB,OD⊥BD,∴∠OBD=30°,∴∠ABD=∠ABC-∠OBD=80°-30°=50°.同理可得,∠OBE=30°,∴∠ABE=∠ABC+∠OBE=80°+30°=110°.综上,射线BA绕点B按顺时针旋转的度数为50°或110°.
16. 【解析】 如图,连接DF,OF,∵∠ACB=90°,AC=6,BC=8,∴AB=10.又∵点D是AB的中点,∴CD=BD=AB=5.∵CD是☉O的直径,∴∠CFD=90°,∴BF=CF=BC=4,∴DF==3.∵OC=OD,CF=BF,∴OF∥AB,∴∠OFC=∠B.∵FG是☉O的切线,∴∠OFG=90°,∴∠OFC+∠BFG=90°,∴∠BFG+∠B=90°,∴FG⊥AB,∴S△BDF=DF·BF=BD·FG,即×3×4=×5×FG,∴FG=.
17.【解析】 (1)连接AC,∵AB=6cm,AD=8cm,∴AC=10cm,
∴点B在☉A内,点C在☉A外,点D在☉A上.
(2)∵以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,∴☉A的半径r的取值范围是6cm18.【解析】 (1)∵点P的坐标为(x,y),P是直线y=2x上的一点,∴y=2x.
∵☉P与直线y=3相切,
∴P点的纵坐标为2或4,
当y=2时,x=1,当y=4时,x=2,
∴点P的坐标为(1,2)或(2,4).
(2)当1当x>2或x<1时,☉P与直线y=3相离.
19.【解析】 (1)连接OD,∵DE是☉O的切线,∴∠ODE=90°,
∴∠ADE+∠BDO=90°.
∵∠ACB=90°,∴∠A+∠B=90°.
∵OD=OB,∴∠B=∠BDO,∴∠ADE=∠A.
(2)连接CD.∵∠ADE=∠A,∴AE=DE.
∵BC是☉O的直径,∠ACB=90°,∴EC是☉O的切线,
∴ED=EC,∴AE=EC.
∵DE=10,∴AC=2DE=20,
在Rt△ADC中,DC==12,
设BD=x,在Rt△BDC中,BC2=x2+122,
在Rt△ABC中,BC2=(x+16)2-202,
∴x2+122=(x+16)2-202,解得x=9,
∴BC==15.
20.【解析】 (1)如图1,连接OB,∵MA,MB分别切☉O于点A,B,
∴∠OBM=∠OAM=90°.
∵∠BOC=2∠BAC=46°,
∴∠BOA=180°-46°=134°,
∴∠AMB=360°-90°-90°-134°=46°.
(2)如图2,连接AD,AB.
∵BD∥AM,DB=AM,
∴四边形BMAD是平行四边形,∴BM=AD.
∵MA切☉O于点A,∴AC⊥AM.∵BD∥AM,∴BD⊥AC.
∵AC为直径,∴BE=DE,∴AB=AD=BM.
∵MA,MB分别切☉O于点A,B,∴MA=MB,∴BM=MA=AB,∴△BMA是等边三角形,∴∠AMB=60°.
21.【解析】 (1)如图,连接BD,∵AB是☉O的直径,
∴∠ACB=∠ADB=90°.
∵CD平分∠ACB,∴∠ACD=∠DCB=45°,
∴∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,
∴△ADB是等腰直角三角形.
∵AB=10,∴AD=BD==5.
在Rt△ACB中,AB=10,BC=5,
∴AC==5.
(2)直线PC与☉O相切.理由如下:
如图,连接OC.在Rt△ACB中,AB=10,BC=5,
∴∠BAC=30°.
∵OA=OC,∴∠OCA=∠OAC=30°,∴∠COB=60°.
∵∠ACD=45°,∴∠OCD=45°-30°=15°,
∴∠CEP=∠COB+∠OCD=60°+15°=75°.
∵PC=PE,∴∠PCE=∠CEP=75°,
∴∠OCP=∠OCD+∠ECP=15°+75°=90°,
∴直线PC与☉O相切.
22.【解析】 (1)2
解法提示:∵OF=2,∠GFO=30°,
∴在Rt△GOF中,OG=OF·tan30°=2.
(2)①连接OB,OP,如图1,
∵PB为☉O的切线,
∴OB⊥PB,∴∠PBO=90°.
在Rt△POB中,OB=1,
∴PB==,
∴当OP取最小值时,PB的值最小.
易知当OP⊥FG时,OP取得最小值,
在Rt△OPF中,OF=2,∠OFP=30°,
∴OP=OF=,
∴PB的最小值为=.
②连接PO并延长,交☉O于点D,连接OB,BD,AD,如图2,
则∠BDA=∠BCA=54°.
∵PA,PB分别切☉O于点A,B,
∴∠BDO=∠ADO=27°,∠OBP=90°,
∴∠BOP=2∠BDO=54°,
∴∠BPO=90°-54°=36°,
∴∠APB=2∠BPO=72°.
③存在.
∵PA,PB为☉O的切线,
∴OP平分∠APB,
∴∠OPB=∠APB=×60°=30°.
在Rt△OPB中,OB=1,∠OPB=30°,
∴OP=2OB=2.
∵OG=2,
∴当点P在点G的位置时,满足要求,此时PF=GF=4.
当点P不与点G重合时,
∵∠OFG=30°,∴∠OGF=60°.
∵OP=OG=2,∴△OPG为等边三角形,
∴PG=OP=2,∴PF=2.
综上所述,PF的长为2或4.
21世纪教育网(www.21cnjy.com)
冀教版九年级数学下册第29章 直线与圆的位置关系单元测试卷
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中,只有一项是符合题目要求的)
1.若☉O的半径为7cm,圆心O到直线l的距离为8cm,则直线l与☉O的位置关系是 ( )
A.相交 B.相切 C.相离 D.不确定
2.☉O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与☉O的位置关系是 ( )
A.点P在☉O内 B.点P的☉O上
C.点P在☉O外 D.点P在☉O上或☉O外
3.如图,在半径为2的☉O中,C为直径AB延长线上一点,CD与☉O相切于点D,连接AD,已知∠DAC=30°,则线段CD的长为 ( )
A.1 B. C.2 D.2
第3题图 第4题图
4.如图,AB是☉O的直径,点C为☉O外一点,CA,CD是☉O的切线,A,D为切点,连接BD,AD.若∠ACD=48°,则∠DBA的大小是 ( )
A.32° B.48° C.60° D.66°
5.如图,边长为a的正六边形内有两个三角形(数据如图),则= ( )
A.3 B.4 C.5 D.6
第5题图 第6题图
6.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,连接OC与半圆相交于点D,则CD的长为 ( )
A.1 B. C.2 D.2
7.在数轴上,点A所表示的实数为3,点B所表示的实数为a,☉A的半径为2.下列说法不正确的是 ( )
A.当a<5时,点B在☉A内 B.当1
8.如图,△ABC是一张周长为17cm的三角形纸片,BC=5cm,☉O是它的内切圆,小明准备用剪刀在☉O的右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm B.7cm
C.6cm D.随直线MN的变化而变化
9.如图,已知P为☉O外一点,连接OP交☉O于点A,且OA=2AP,求作直线PB,使PB与☉O相切.以下是甲、乙两同学的作法.
甲:作OP的中垂线,交☉O于点B,则直线PB即所求.
乙:取OP的中点M,以M为圆心、OM长为半径画弧,交☉O于点B,则直线PB即所求.
对于两人的作法,下列说法正确的是 ( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
第9题图 第10题图
10.如图,等腰三角形ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也停止.设运动时间为t(s),以点O为圆心,OB长为半径的☉O与BA交于另一点E,连接ED.当直线DE与☉O相切时,t的取值是 ( )
A. B. C. D.
11.如图,圆内接正八边形的边长为1,以正八边形的一边AB作正方形ABCD,将正方形ABCD绕点B顺时针旋转,使BC与正八边形的另一边BC'重合,则正方形ABCD与正方形A'BC'D'重叠部分的面积为 ( )
A. B.-1 C. D.
第11题图 第12题图
12.如图,已知△ABC,以AB为直径的☉O交AC于点E,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下结论:①DF是☉O的切线;②CF=EF;③=.其中正确结论的序号是 ( )
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题共4小题,每小题3分,共12分)
13.如图,正八边形ABCDEFGH内接于☉O,点P是上的任意一点,则∠CPE的度数为 .?
第13题图 第14题图
14.如图,P是△ABC的内心,连接PA,PB,PC,△PAB,△PBC,△PAC的面积分别为S1,S2,S3.则S1 S2+S3.(填“<”“=”或“>”)?
15.如图,∠ABC=80°,O为射线BC上一点,以点O为圆心、OB长为半径作☉O,要使射线BA与☉O相切,应将射线BA绕点B按顺时针方向旋转的度数为 .?
第15题图 第16题图
16.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB的中点,以CD为直径作☉O,☉O分别与AC,BC交于点E,F,过点F作☉O的切线FG,交AB于点G,则FG的长为 .?
三、解答题(本大题共6小题,共52分)
17.(本小题满分7分)
已知矩形ABCD的边AB=6cm,AD=8cm.
(1)以点A为圆心、8cm为半径作☉A,求点B,C,D与☉A的位置关系;
(2)若以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,求☉A的半径r的取值范围.
18.(本小题满分7分)
如图,P是直线y=2x上的一点,以点P为圆心、1个单位长度为半径作☉P,设点P的坐标为(x,y).
(1)求当x为何值时,☉P与直线y=3相切,并求点P的坐标;
(2)直接写出当x为何值时,☉P与直线y=3相交、相离.
19.(本小题满分8分)
如图,在Rt△ABC中,∠C=90°,以BC为直径的☉O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.
20.(本小题满分8分)
已知☉O中,AC为直径,MA,MB分别切☉O于点A,B.
(1)如图1,若∠BAC=23°,求∠AMB的大小;
(2)如图2,过点B作BD∥MA,交AC于点E,交☉O于点D,若BD=MA,求∠AMB的大小.
21.(本小题满分10分)
如图,☉O的直径AB为10cm,弦BC为5cm,D,E分别是∠ACB的平分线与☉O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC,AD的长;
(2)试判断PC与☉O的位置关系,并说明理由.
22.(本小题满分12分)
如图1,在Rt△OGF中,∠GOF=90°,OF=2,∠GFO=30°.
(1)OG= ;?
(2)若☉O的半径为1,交直线OF于点C,点P是直线GF上的动点,PA,PB分别切☉O于点A,B.
①求PB的最小值;
②连接BC,AC,如图2所示,若∠BCA=54°,求∠APB的度数;
③在直线GF上是否存在点P,使得∠APB=60°?若存在,请求出FP的长;若不存在,请说明理由.
图1 图2
参 考 答 案 与 解 析
1.C 【解析】 ∵☉O的半径为7cm,圆心O到直线l的距离为8cm,7<8,∴直线l与☉O相离.故选C.
2.A 【解析】 ∵圆心O的坐标为(0,0),点P的坐标为(4,2),∴OP==<5,∴点P在☉O内.故选A.
3.D 【解析】 连接OD,∵OA=OD,∴∠OAD=∠ODA=30°.∵CD与☉O相切于点D,∴OD⊥CD.∵∠DOC=2∠DAC=2×30°=60°,∴∠C=30°,∴CD=OD=2.故选D.
4.D 【解析】 ∵CA,CD是☉O的切线,∴CA=CD.∵∠ACD=48°,∴∠CAD=∠CDA=66°.∵CA⊥AB,AB是直径,∴∠ADB=∠CAB=90°,∴∠DBA+∠DAB=90°,∠CAD+∠DAB=90°,∴∠DBA=∠CAD=66°,故选D.
5.C 【解析】 解法一 如图,设正六边形的中心为O.连接OA,OB.∵∠AOB=360°÷6=60°,OA=OB,∴△OAB是等边三角形,易知S正六边形=6S△OAB.∵图中的两个直角三角形可拼成一个边长为a的等边三角形,∴S空白=S△OAB,∴=====5.
解法二 通过割补题图可得如图所示的图形,所以=5.
6.C 【解析】 如图,设☉O与AC相切于点E,连接OE,则OE⊥AC,∵AB=10,AC=8,BC=6,∴AB2=AC2+BC2,∴∠ACB=90°,∴BC⊥AC,∴OE∥BC.由AO=OB=AB,易知OE=BC=3,∴OD=3.在Rt△ABC中,OC是斜边AB上的中线,∴OC=AB=5,∴CD=OC-OD=5-3=2.故选C.
7.A 【解析】 设点A,B之间的距离为d,由于圆心A在数轴上所表示的实数为3,圆的半径r=2,所以当d=r时,☉A与数轴交于两点,所表示的实数分别是1和5,故当a=1或a=5时,点B在☉A上;当d
8.B 【解析】 如图,设D,E,F分别是☉O的切点,∵☉O是△ABC的内切圆,BC=5cm,∴BD+CE=BC=5cm,∵AB+BC+AC=17cm,∴AD+AE=7cm.∵DM=MF,FN=EN,∴AM+AN+MN=AD+AE=7cm.故选B.
9.D 【解析】 如图1,作OP的垂直平分线交OP于点H,连接OB,设AP=x,则OA=2x,OB=2x.∵BH垂直平分OP,∴BO=BP=2x.∵OB2+BP2=(2x)2+(2x)2=8x2,OP2=(3x)2=9x2,∴△OBP不是直角三角形,∴PB不是☉O的切线,∴甲的作法错误.如图2,连接OB,∵点M为OP的中点,∴OP为☉M的直径,∴∠OBP=90°,∴OB⊥PB,∴PB与☉O相切,∴乙的作法正确.故选D.
10.A 【解析】 如图,作AH⊥BC于H,依题意得BE=2tcm,BD=(8-2t)cm.∵AB=AC=5cm,BC=8cm,∴BH=CH=BC=4cm.当BE⊥DE时,直线DE与☉O相切,则∠BED=90°,又∵∠EBD=∠ABH,∴△BED∽△BHA,∴=,即=,解得t=.故选A.
11.B 【解析】 正八边形的内角∠ABC'==135°,正方形ABCD绕点B顺时针旋转,使BC与正八边形的另一边BC'重合,设CD与A'D'相交于点E,∴∠ABC=∠A'BC'=90°,∠BA'D'=∠BAD=90°,∴∠ABA'=135°-90°=45°.延长BA',则BA'过点D,如图,则∠A'DE=∠ABA'=∠A'ED=45°,∴A'E=A'D.∵AB=1,∴A'B=AB=1,BD=,∴A'E=A'D=-1,∴正方形ABCD与正方形A'BC'D'重叠部分的面积=S△BDC-S△DA'E=×1×1-×(-1)×(-1)=-1.故选B.
12.A 【解析】 如图,连接OD,DE,AD,∵DB=DC,∴OD是△ABC的中位线,∴OD∥AC.∵DF⊥AC,∴DF⊥OD,∴DF是☉O的切线,故①正确.∵∠CED+∠AED=180°,∠B+∠AED=180°,∴∠CED=∠B.∵AB是☉O的直径,∴∠ADB=90°,即AD⊥BC.∵BD=CD,∴AB=AC,∴∠B=∠C,∴∠CED=∠C,∴DC=DE.又∵DF⊥AC,∴CF=EF,故②正确.当∠EAD=∠EDA时,=,此时△ABC为等边三角形,当△ABC不是等边三角形时,∠EAD≠∠EDA,则≠,∴=不一定正确.综上,正确结论的序号是①②.故选A.
13.45° 【解析】 连接OD,OC,OE,∵八边形ABCDEFGH是正八边形,∴∠COD=∠DOE==45°,∴∠COE=45°+45°=90°,∴∠CPE=∠COE=45°.
14.< 【解析】 过点P作三边的垂线PD,PE,PF,根据点P是△ABC的内心,可得PD=PE=PF,设PD=PE=PF=h,则S1=AB·h,S2+S3=(AC+BC)·h,根据三角形的两边之和大于第三边,得S1
16. 【解析】 如图,连接DF,OF,∵∠ACB=90°,AC=6,BC=8,∴AB=10.又∵点D是AB的中点,∴CD=BD=AB=5.∵CD是☉O的直径,∴∠CFD=90°,∴BF=CF=BC=4,∴DF==3.∵OC=OD,CF=BF,∴OF∥AB,∴∠OFC=∠B.∵FG是☉O的切线,∴∠OFG=90°,∴∠OFC+∠BFG=90°,∴∠BFG+∠B=90°,∴FG⊥AB,∴S△BDF=DF·BF=BD·FG,即×3×4=×5×FG,∴FG=.
17.【解析】 (1)连接AC,∵AB=6cm,AD=8cm,∴AC=10cm,
∴点B在☉A内,点C在☉A外,点D在☉A上.
(2)∵以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,∴☉A的半径r的取值范围是6cm
∵☉P与直线y=3相切,
∴P点的纵坐标为2或4,
当y=2时,x=1,当y=4时,x=2,
∴点P的坐标为(1,2)或(2,4).
(2)当1
19.【解析】 (1)连接OD,∵DE是☉O的切线,∴∠ODE=90°,
∴∠ADE+∠BDO=90°.
∵∠ACB=90°,∴∠A+∠B=90°.
∵OD=OB,∴∠B=∠BDO,∴∠ADE=∠A.
(2)连接CD.∵∠ADE=∠A,∴AE=DE.
∵BC是☉O的直径,∠ACB=90°,∴EC是☉O的切线,
∴ED=EC,∴AE=EC.
∵DE=10,∴AC=2DE=20,
在Rt△ADC中,DC==12,
设BD=x,在Rt△BDC中,BC2=x2+122,
在Rt△ABC中,BC2=(x+16)2-202,
∴x2+122=(x+16)2-202,解得x=9,
∴BC==15.
20.【解析】 (1)如图1,连接OB,∵MA,MB分别切☉O于点A,B,
∴∠OBM=∠OAM=90°.
∵∠BOC=2∠BAC=46°,
∴∠BOA=180°-46°=134°,
∴∠AMB=360°-90°-90°-134°=46°.
(2)如图2,连接AD,AB.
∵BD∥AM,DB=AM,
∴四边形BMAD是平行四边形,∴BM=AD.
∵MA切☉O于点A,∴AC⊥AM.∵BD∥AM,∴BD⊥AC.
∵AC为直径,∴BE=DE,∴AB=AD=BM.
∵MA,MB分别切☉O于点A,B,∴MA=MB,∴BM=MA=AB,∴△BMA是等边三角形,∴∠AMB=60°.
21.【解析】 (1)如图,连接BD,∵AB是☉O的直径,
∴∠ACB=∠ADB=90°.
∵CD平分∠ACB,∴∠ACD=∠DCB=45°,
∴∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,
∴△ADB是等腰直角三角形.
∵AB=10,∴AD=BD==5.
在Rt△ACB中,AB=10,BC=5,
∴AC==5.
(2)直线PC与☉O相切.理由如下:
如图,连接OC.在Rt△ACB中,AB=10,BC=5,
∴∠BAC=30°.
∵OA=OC,∴∠OCA=∠OAC=30°,∴∠COB=60°.
∵∠ACD=45°,∴∠OCD=45°-30°=15°,
∴∠CEP=∠COB+∠OCD=60°+15°=75°.
∵PC=PE,∴∠PCE=∠CEP=75°,
∴∠OCP=∠OCD+∠ECP=15°+75°=90°,
∴直线PC与☉O相切.
22.【解析】 (1)2
解法提示:∵OF=2,∠GFO=30°,
∴在Rt△GOF中,OG=OF·tan30°=2.
(2)①连接OB,OP,如图1,
∵PB为☉O的切线,
∴OB⊥PB,∴∠PBO=90°.
在Rt△POB中,OB=1,
∴PB==,
∴当OP取最小值时,PB的值最小.
易知当OP⊥FG时,OP取得最小值,
在Rt△OPF中,OF=2,∠OFP=30°,
∴OP=OF=,
∴PB的最小值为=.
②连接PO并延长,交☉O于点D,连接OB,BD,AD,如图2,
则∠BDA=∠BCA=54°.
∵PA,PB分别切☉O于点A,B,
∴∠BDO=∠ADO=27°,∠OBP=90°,
∴∠BOP=2∠BDO=54°,
∴∠BPO=90°-54°=36°,
∴∠APB=2∠BPO=72°.
③存在.
∵PA,PB为☉O的切线,
∴OP平分∠APB,
∴∠OPB=∠APB=×60°=30°.
在Rt△OPB中,OB=1,∠OPB=30°,
∴OP=2OB=2.
∵OG=2,
∴当点P在点G的位置时,满足要求,此时PF=GF=4.
当点P不与点G重合时,
∵∠OFG=30°,∴∠OGF=60°.
∵OP=OG=2,∴△OPG为等边三角形,
∴PG=OP=2,∴PF=2.
综上所述,PF的长为2或4.
21世纪教育网(www.21cnjy.com)
