华东师大版八年级上册数学13.5.2 线段垂直平分线(共28张PPT)
文档属性
| 名称 | 华东师大版八年级上册数学13.5.2 线段垂直平分线(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 701.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 15:41:28 | ||
图片预览







文档简介
(共28张PPT)
第13章
全等三角形
13.5
逆命题与逆定理
第2课时
线段垂直平分线
引入
我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴,并知道线段的垂直平分线上的点到这条线段的两个端点的距离相等.我们也可以用逻辑推理的方法证明这一结论.
探究新知
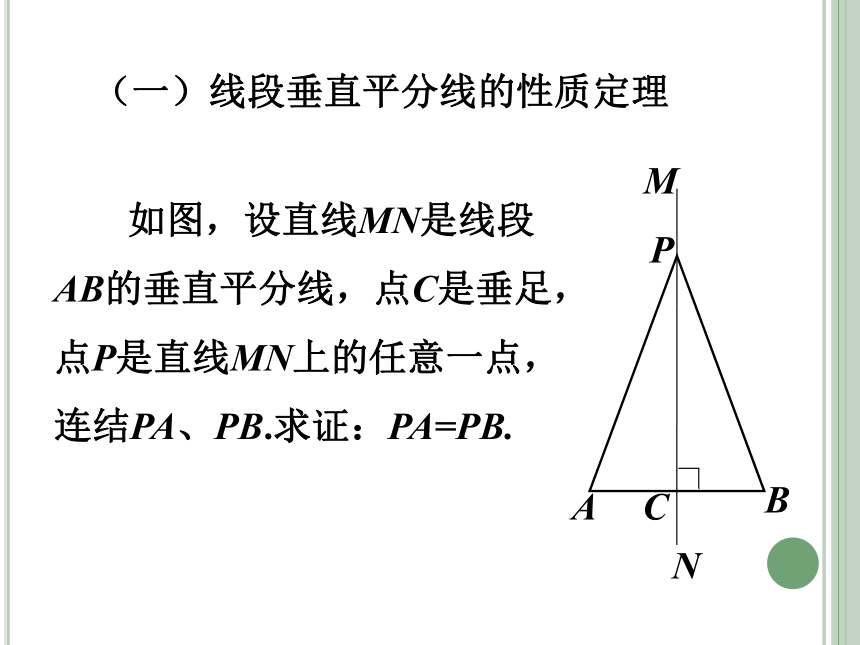
(一)线段垂直平分线的性质定理
如图,设直线MN是线段AB的垂直平分线,点C是垂足,点P是直线MN上的任意一点,连结PA、PB.求证:PA=PB.
B
A
C
N
M
P
过程
证明:在△APC
和△BPC
中,
∵PC=PC,∠PCB=∠PCA,AC=BC,
∴△APC≌△BPC(S.A.S.).
∴PA=PB.
B
A
C
N
M
P
已知:MN⊥AB,垂足为点C,AC=BC,点P是直线MN上任意一点.
求证:PA=PB.
定理
线段的垂直平分线上的点到这条线段的两个端点的距离相等.
(二)线段垂直平分线的判定定理
上述命题的逆命题应当怎样表述?
逆命题:到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.
思考
如果有一点到一条线段的两个端点的距离相等,那么这一点在这条线段的垂直平分线上.
将其改写成“如果……,那么……”的形式.
命题:到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.
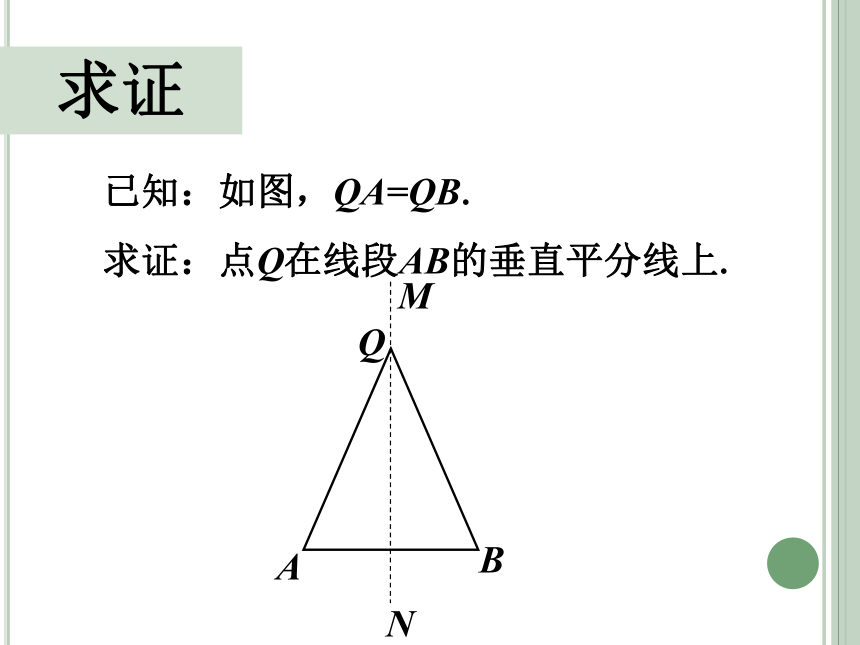
求证
已知:如图,QA=QB.
求证:点Q在线段AB的垂直平分线上.
N
A
Q
B
M
证明
证明:设点C为线段AB的中点,连结QC,在△ACQ与△BCQ中,
∵QA=QB,AC=BC,QC=QC,
∴
△ACQ≌△BCQ,
∴∠QCA=∠QCB.
又∵∠QCA+∠QCB=180°,
∴
∠QCA=∠QCB=90°.
∴QC垂直平分线段AB.
∴点Q在线段AB垂直平分线上.
A
C
N
M
Q
B
小结
到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.
上述两条定理互为逆定理,根据上述两条定理,我们很容易证明:三角形三边的垂直平分线交于一点.
(三)三角形三边的垂直平分线交于一点
线段的垂直平分线上的点到这条线段的两个端点的距离相等.
到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.
求证
已知:△ABC中,AB的垂直平分线l与AC的垂直平分线n相交于一点O.
求证:点O在BC的垂直平分线上.
A
B
C
O
l
m
n
证明
证明:连结OA、OB、OC.
∵O是AB的垂直平分线l上的一点,
∴OA=OB.
∵O是AC的垂直平分线n上的一点,
∴OA=OC.
∴OB=OC.
∴O在线段BC的垂直平分线上.
A
B
C
O
l
m
n
随堂练习
练习
1.如图,已知点A、B和直线l,在直线l上求作一点P,使PA=PB.
l
A
B
.
.
P
练习
2.如图,BD⊥AC,垂足为E,AE=CE.求证:AB+CD=AD+BC.
A
B
C
D
E
证明:∵BD⊥AC,AE=CE,
∴BD是线段AC的垂直平分线.
∵B、D在垂直平分线上,
∴AD=DC,AB=CB,
∴AB+CD=AD+BC.
练习
3.如图,在△ABC中,点D在BC上,且BD+AD=BC.求证:点D在AC垂直平分线上.
A
B
C
D
证明:∵BD+AD=BC,BD+DC=BC,
∴AD=DC,
∴△ADC是等腰三角形,
∴点D在AC的垂直平分线上.
课时总结
小结
会证明线段垂直平分线的性质定理与判断定理.
布置作业
作业
1.教材第99页习题13.5第2题.
作业
2.备选习题
(1)到△ABC三个顶点的距离相等的点的位置是在
(
)
A.三角形的内部
B.三角形的外部
C.三角形的边上
D.以上三种都有可能
作业
2.备选习题
(2)如图,线段MN与线段AB交于点O,给出下列条件:①MN=MB,OA=OB;
②MA=MB,NA=NB;
③∠AMO=∠BMO,∠MAO=∠MBO;④∠AMO=∠BMO,∠ANO=∠BNO.其中能说明MN是AB垂直平分线的是
(
)
A.
①③
B.
②③④
C.
①②
D.
①②③④
M
A
B
N
O
作业
2.备选习题
(3)在等腰直角△ABC中,AB=AC,BC=a,其斜边上的中线与一腰的垂直平分线交于点O,则点O到三角形三个顶点的距离是
.
作业
2.备选习题
(4)如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形共有
对.
A
B
C
D
E
作业
2.备选习题
(5)如图,已知△ABC中,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连结EC,EA=EC.求证:BA=BC.
A
B
C
D
E
F
作业
2.备选习题
(6)如图,A、B两个村子在河CD同侧,A、B两村子到河CD的距离分别为AC=1
km,BD=3
km,且CD=3
km.现要在河边CD上建一水厂,向A、B两村输送自来水,铺设水管的工程费用为每千米2万元.请你在CD上确定水厂的位置,使铺设水管的费用最少,并求出铺设水管的总费用.
A
B
C
D
第13章
全等三角形
13.5
逆命题与逆定理
第2课时
线段垂直平分线
引入
我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴,并知道线段的垂直平分线上的点到这条线段的两个端点的距离相等.我们也可以用逻辑推理的方法证明这一结论.
探究新知
(一)线段垂直平分线的性质定理
如图,设直线MN是线段AB的垂直平分线,点C是垂足,点P是直线MN上的任意一点,连结PA、PB.求证:PA=PB.
B
A
C
N
M
P
过程
证明:在△APC
和△BPC
中,
∵PC=PC,∠PCB=∠PCA,AC=BC,
∴△APC≌△BPC(S.A.S.).
∴PA=PB.
B
A
C
N
M
P
已知:MN⊥AB,垂足为点C,AC=BC,点P是直线MN上任意一点.
求证:PA=PB.
定理
线段的垂直平分线上的点到这条线段的两个端点的距离相等.
(二)线段垂直平分线的判定定理
上述命题的逆命题应当怎样表述?
逆命题:到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.
思考
如果有一点到一条线段的两个端点的距离相等,那么这一点在这条线段的垂直平分线上.
将其改写成“如果……,那么……”的形式.
命题:到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.
求证
已知:如图,QA=QB.
求证:点Q在线段AB的垂直平分线上.
N
A
Q
B
M
证明
证明:设点C为线段AB的中点,连结QC,在△ACQ与△BCQ中,
∵QA=QB,AC=BC,QC=QC,
∴
△ACQ≌△BCQ,
∴∠QCA=∠QCB.
又∵∠QCA+∠QCB=180°,
∴
∠QCA=∠QCB=90°.
∴QC垂直平分线段AB.
∴点Q在线段AB垂直平分线上.
A
C
N
M
Q
B
小结
到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.
上述两条定理互为逆定理,根据上述两条定理,我们很容易证明:三角形三边的垂直平分线交于一点.
(三)三角形三边的垂直平分线交于一点
线段的垂直平分线上的点到这条线段的两个端点的距离相等.
到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.
求证
已知:△ABC中,AB的垂直平分线l与AC的垂直平分线n相交于一点O.
求证:点O在BC的垂直平分线上.
A
B
C
O
l
m
n
证明
证明:连结OA、OB、OC.
∵O是AB的垂直平分线l上的一点,
∴OA=OB.
∵O是AC的垂直平分线n上的一点,
∴OA=OC.
∴OB=OC.
∴O在线段BC的垂直平分线上.
A
B
C
O
l
m
n
随堂练习
练习
1.如图,已知点A、B和直线l,在直线l上求作一点P,使PA=PB.
l
A
B
.
.
P
练习
2.如图,BD⊥AC,垂足为E,AE=CE.求证:AB+CD=AD+BC.
A
B
C
D
E
证明:∵BD⊥AC,AE=CE,
∴BD是线段AC的垂直平分线.
∵B、D在垂直平分线上,
∴AD=DC,AB=CB,
∴AB+CD=AD+BC.
练习
3.如图,在△ABC中,点D在BC上,且BD+AD=BC.求证:点D在AC垂直平分线上.
A
B
C
D
证明:∵BD+AD=BC,BD+DC=BC,
∴AD=DC,
∴△ADC是等腰三角形,
∴点D在AC的垂直平分线上.
课时总结
小结
会证明线段垂直平分线的性质定理与判断定理.
布置作业
作业
1.教材第99页习题13.5第2题.
作业
2.备选习题
(1)到△ABC三个顶点的距离相等的点的位置是在
(
)
A.三角形的内部
B.三角形的外部
C.三角形的边上
D.以上三种都有可能
作业
2.备选习题
(2)如图,线段MN与线段AB交于点O,给出下列条件:①MN=MB,OA=OB;
②MA=MB,NA=NB;
③∠AMO=∠BMO,∠MAO=∠MBO;④∠AMO=∠BMO,∠ANO=∠BNO.其中能说明MN是AB垂直平分线的是
(
)
A.
①③
B.
②③④
C.
①②
D.
①②③④
M
A
B
N
O
作业
2.备选习题
(3)在等腰直角△ABC中,AB=AC,BC=a,其斜边上的中线与一腰的垂直平分线交于点O,则点O到三角形三个顶点的距离是
.
作业
2.备选习题
(4)如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形共有
对.
A
B
C
D
E
作业
2.备选习题
(5)如图,已知△ABC中,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连结EC,EA=EC.求证:BA=BC.
A
B
C
D
E
F
作业
2.备选习题
(6)如图,A、B两个村子在河CD同侧,A、B两村子到河CD的距离分别为AC=1
km,BD=3
km,且CD=3
km.现要在河边CD上建一水厂,向A、B两村输送自来水,铺设水管的工程费用为每千米2万元.请你在CD上确定水厂的位置,使铺设水管的费用最少,并求出铺设水管的总费用.
A
B
C
D
