苏科版八年级数学上册第三章《勾股定理》填空题苏州历年试题汇编(Word版 含解析)
文档属性
| 名称 | 苏科版八年级数学上册第三章《勾股定理》填空题苏州历年试题汇编(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 23:18:02 | ||
图片预览



文档简介
第三章《勾股定理》填空题苏州历年试题汇编
一.直角三角形的性质
1.(2016春?工业园区期中)如图,已知点P是射线ON上一动点(即P可在射线ON上运动),∠AON=30°,当∠A=
时,△AOP为直角三角形.
二.勾股定理
2.(2020春?相城区期末)如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当AD平分∠BAC时,AP的长为
.
3.(2019秋?太仓市期末)如图示,在Rt△ABC中,∠ACB=90°,AC=3,BC=,点P在Rt△ABC内部,且∠PAB=∠PBC,连接CP,则CP的最小值等于
.
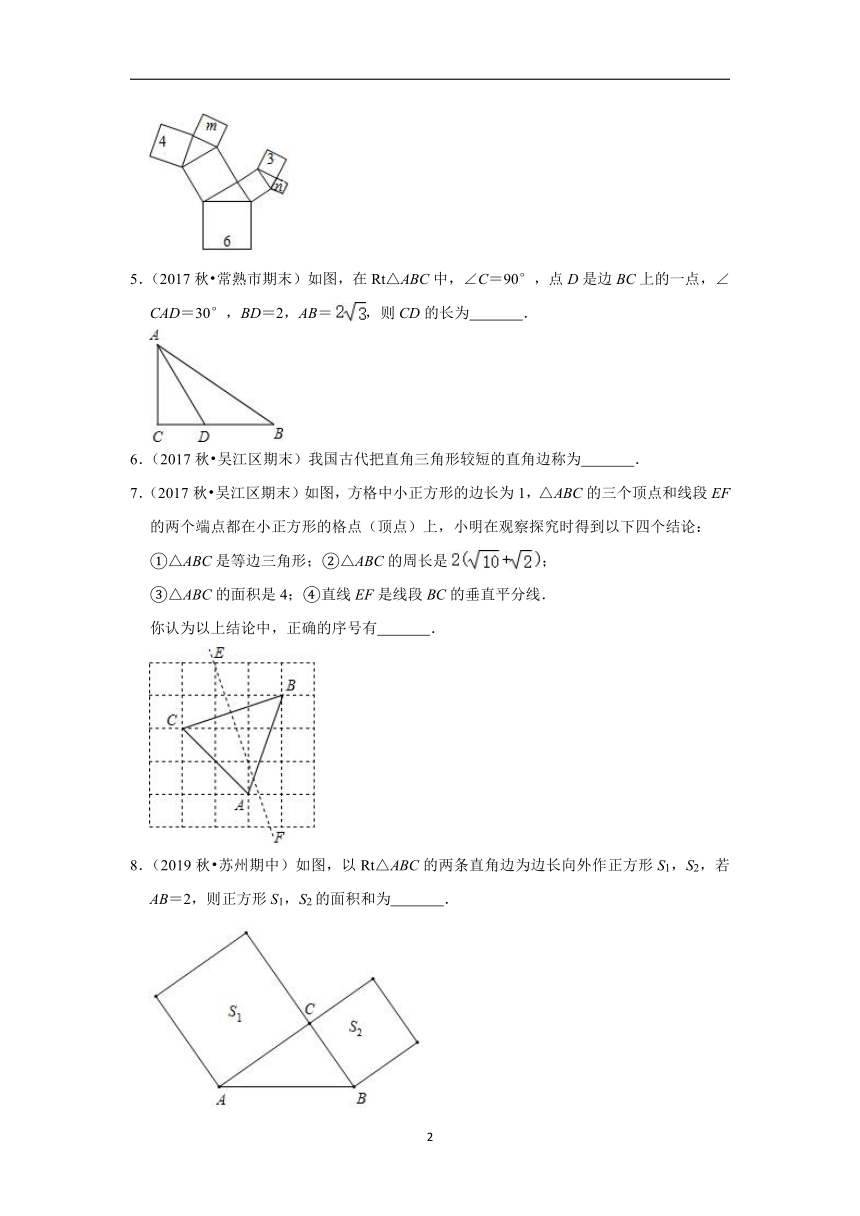
4.(2017秋?苏州期末)在如图所示的“勾股树”中,已知正方形内的数字或字母表示该正方形的边长,由此可以计算:m2+n2=
.
5.(2017秋?常熟市期末)如图,在Rt△ABC中,∠C=90°,点D是边BC上的一点,∠CAD=30°,BD=2,AB=,则CD的长为
.
6.(2017秋?吴江区期末)我国古代把直角三角形较短的直角边称为
.
7.(2017秋?吴江区期末)如图,方格中小正方形的边长为1,△ABC的三个顶点和线段EF的两个端点都在小正方形的格点(顶点)上,小明在观察探究时得到以下四个结论:
①△ABC是等边三角形;②△ABC的周长是;
③△ABC的面积是4;④直线EF是线段BC的垂直平分线.
你认为以上结论中,正确的序号有
.
8.(2019秋?苏州期中)如图,以Rt△ABC的两条直角边为边长向外作正方形S1,S2,若AB=2,则正方形S1,S2的面积和为
.
9.(2018秋?吴江区期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=32,AB=40,且BD:DC=5:3.则△ADB的面积为
.
10.(2017秋?相城区期中)如图,在Rt△ABC中∠B=90°,AC=25,BC=15,以AC,BC为直径的半圆的面积分别为S1,S2,则S1﹣S2=
.(结果保留π)
11.(2017秋?张家港市校级期中)若等腰三角形中腰长为10cm,第三边长为16cm,那么第三边上的高为
.
12.(2017秋?太仓市校级期中)如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD2=
.
13.(2017秋?太仓市期中)在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,a=5,b=12,则c=
.
14.(2016秋?虎丘区校级期中)如图,Rt△ABC,∠ACB=90°,以三边为边长向外作正方形,64、400分别为所在正方形的面积,则图中字母S所代表的正方形面积是
.
15.(2016秋?吴中区期中)已知直角三角形的两边长为3cm、5cm,则它的第三边长为
.
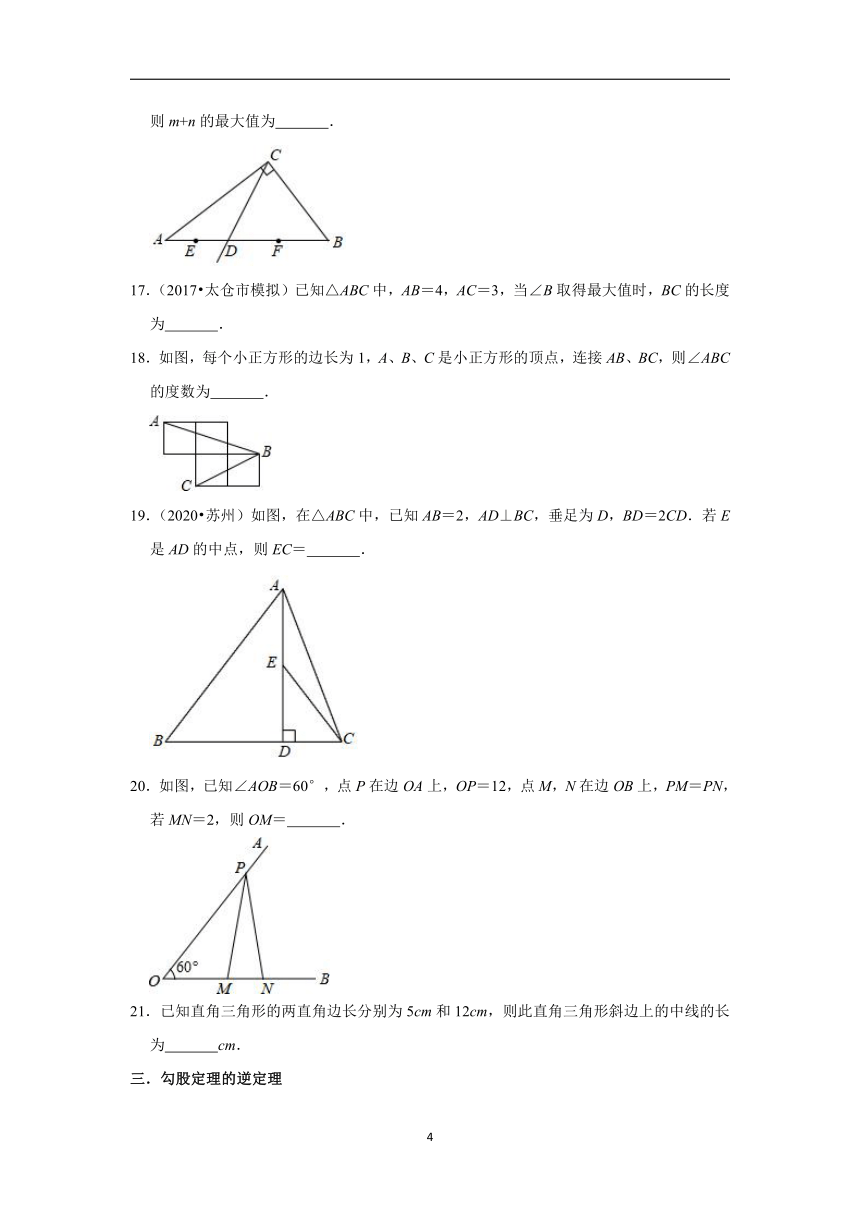
16.(2020?姑苏区一模)如图,△ABC中,∠ACB=90°,AC=4,BC=3,射线CD与边AB交于点D,E、F分别为AD、BD中点,设点E、F到射线CD的距离分别为m、n,则m+n的最大值为
.
17.(2017?太仓市模拟)已知△ABC中,AB=4,AC=3,当∠B取得最大值时,BC的长度为
.
18.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,连接AB、BC,则∠ABC的度数为
.
19.(2020?苏州)如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC=
.
20.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
.
21.已知直角三角形的两直角边长分别为5cm和12cm,则此直角三角形斜边上的中线的长为
cm.
三.勾股定理的逆定理
22.(2017秋?高新区期末)一个三角形的三边长之比是5:12:13,且周长是60,则它的面积是
.
23.(2016秋?吴江区期中)三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是
.
四.等腰直角三角形
24.(2020春?工业园区期末)如图,四边形纸片ABCD中,AB=BC,∠ABC=∠ADC=90°.若该纸片的面积为10cm2,则对角线BD=
cm.
25.(2020春?常熟市期末)如图,在五边形ABCDE中,∠A=∠ABC=90°,AE=,BC=6,连接CE,BD.若CE⊥CD且CE=CD,则△BCD的面积为
.
26.(2018秋?苏州期末)如图,△ABC为等腰直角三角形,∠ABC=90°,△ADB为等边三角形,则∠ADC=
°.
27.(2019秋?苏州期中)如图,△ABC中,∠C=90°,点D为AC上一点,∠ABD=2∠BAC=45°,若AD=12,则△ABD的面积为
.
28.(2019秋?苏州期中)如图,一块含有45°角的直角三角板,外框的一条直角边长为6cm,三角板的外框线和与其平行的内框线之间的距离均为cm,则图中阴影部分的面积为
cm2(结果保留根号).
29.(2019?张家港市模拟)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°),按如图所示的位置摆放,若∠1=55°,则∠2的度数为
.
30.(2018?昆山市一模)如图,在等腰Rt△ABC中,∠ACB=90°,AB=4,点E为AB的中点.以AE为边作等边△ADE(点D与点C分别在AB的异侧),连接CD.则△ACD的面积为
.
31.(2016?苏州二模)如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是
.
32.如图,以OA为斜边作等腰Rt△OAB,再以OB为斜边在△OAB外侧作等腰Rt△OBC,如此继续,得到8个等腰直角三角形,则△OAB与△OHI面积的比值是
.
答案与解析
一.直角三角形的性质
1.【分析】根据点P的运动轨迹,分∠APO是直角和锐角两种情况讨论求解.
【解答】解:若∠APO是直角,则∠A=90°﹣∠AON=90°﹣30°=60°,
若∠APO是锐角,∵∠AON=30°是锐角,
∴∠A=90°,
综上所述,∠A=60°或90°.
故答案为:60°或90°.
二.勾股定理(共20小题)
2.【分析】根据勾股定理求出AC,根据角平分线的定义、平行线的性质得到∠ADP=∠PAD,得到PA=PD,根据相似三角形的性质列出比例式,计算即可.
【解答】解:∵∠C=90°,AB=5,BC=4,
∴AC==3,
∵PQ∥AB,
∴∠BAD=∠ADP,
又∵AD平分∠BAC,
∴∠BAD=∠PAD,
∴∠ADP=∠PAD,
∴PA=PD,
∴QP=2PA,
∵PQ∥AB,
∴△CPQ∽△CAB,
∴=,即=,
解得PA=.
故答案为:.
3.【分析】构造点P在以AB为弦的圆上,首先求得∠APB=120°,然后求得半径和OC的长,当点O、P、C在一条直线上时,CP有最小值.
【解答】解:如图所示,
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=,
∴tan∠BAC==,
∴∠BAC=30°,
∴∠CBA=60°,即∠1+∠2=60°,
∵∠PAB=∠1,
∴∠PAB+∠2=60°,
∴∠APB=120°,
∴点P在以AB为弦的圆O上,
∴∠AOB=120°,
∵OA=OB,
∴∠3=∠4=30°,
∴∠1+∠2+∠3=90°,即∠CBO=90°,
∠DAO=∠BAC+∠4=60°,∠AOD=30°,
过点O作OD⊥AC于点D,
∴∠DOB=90°,
∵∠DCB=90°,
∴四边形DCBO是矩形,
∴DC=OB,OD=BC=,
∴在Rt△ADO中,AD=OD?tan30°=×=1,
∴DC=AC﹣DC=3﹣1=2,
∴OB=OP=2,
∴OC===,
当点O、P、C在一条直线上时,CP有最小值,
∴CP的最小值为OC﹣OP=﹣2.
故答案为﹣2.
4.【分析】根据勾股定理和正方形的面积公式解答.
【解答】解:如图,m2=a2﹣42,n2=b2﹣32,a2+b2=62
则m2+n2=a2﹣42+b2﹣32=62﹣42﹣32=11.
故答案是:11.
5.【分析】设CD=x,根据直角三角形的性质用x表示出AD,根据勾股定理求出AC,再根据勾股定理列方程,解方程得到答案.
【解答】解:设CD=x,
∵∠C=90°,∠CAD=30°,
∴AD=2CD=2x,
由勾股定理得,AC==x,
则(x)2+(x+2)2=12
解得,x1=1,x2=﹣2(舍去)
故答案为:1.
6.【分析】根据勾股定理的概念解答即可.
【解答】解:我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦,
故答案为:勾
7.【分析】根据勾股定理求出AC、BC、AB长,即可判断①和②,求出AC边上的高,即可判断③,证△MTD≌△BZC,推出∠ZBC=∠TMD,能求出EF⊥BC,根据等腰三角形性质即可求出CO=BO,即可判断④.
【解答】解:∵由勾股定理得:AB=,AC=,BC=,
∴AB=BC,
∴△ABC的形状是等腰三角形,∴①错误;
△ABC的周长是++2=2+2,∴②正确;
连接BN,由勾股定理得:AN=CN,
在△BCN和△BAN中
∴△BCN≌△BAN,
∴∠BNC=∠BNA,
∵∠BNC+∠BNA=180°,
∴∠BNC=90°,
由勾股定理得:BN=,
∴△ABC的面积是AC×BN=×2×2=4,∴③正确;
在△MTD和△BZC中
∴△MTD≌△BZC,
∴∠ZBC=∠TMD,
∵∠MTD=90°,
∴∠TDM+∠TMD=∠ZBC+∠BRO=90°,
∴∠ROB=90°,
∴EF⊥BC,
由勾股定理得:BM=CM,
∴CO=BO,
直线EF是线段BC的垂直平分线,∴④正确;
故答案为:②③④.
8.【分析】根据正方形的面积公式和勾股定理得到正方形S1,S2的面积和是斜边AB的平方.
【解答】解:∵以Rt△ABC的两条直角边为边长向外作正方形S1,S2,
∴正方形S1的面积是AC2,正方形S2的面积是BC2,AC2+BC2=AB2,
∴正方形S1,S2的面积和为:AC2+BC2=AB2=22=4.
故答案是:4.
9.【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC,再由BC=32,BD:DC=5:3,CD=×32=12,则DE=12,然后根据三角形面积公式计算即可.
【解答】解:作DE⊥AB于E,如图,
∵∠C=90°,AD平分∠BAC,
∴DE=DC,
∵BC=32,BD:DC=5:3,
∴CD=×32=12,
∴DE=12,
∴△ADB的面积=AB?DE=×40×12=240.
故答案为:240.
10.【分析】根据半圆面积公式,求出S1、S2即可解决问题.
【解答】解:S1=π()2=πAC2=π,S2=πBC2=π,
所以S1﹣S2=50π.
11.【分析】根据等腰三角形的性质先求出BD,然后在RT△ABD中,可根据勾股定理进行求解.
【解答】解:如图:
由题意得:AB=AC=10cm,BC=16cm,
作AD⊥BC于点D,则有DB=BC=8cm,
在Rt△ABD中,AD==6cm.
故答案为:6cm.
12.【分析】根据等式的性质,可得∠BAD与∠CAD′的关系,根据SAS,可得△BAD与△CAD′的关系,根据全等三角形的性质,可得BD与CD′的关系,根据勾股定理,可得答案.
【解答】解:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:
∵∠BAC+∠CAD=∠DAD′+∠CAD,
即∠BAD=∠CAD′,
在△BAD与△CAD′中,
,
∴△BAD≌△CAD′(SAS),
∴BD=CD′.
∠DAD′=90°
由勾股定理得DD′=,
∠D′DA+∠ADC=90°,
由勾股定理得CD′=,
∴BD=CD′=,即BD2=41.
故答案为:41.
13.【分析】在Rt△ABC中,利用勾股定理可求出c的长度即可.
【解答】解:因为在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,a=5,b=12,
所以c===13,
故答案为:13.
14.【分析】要求图中字母S所代表的正方形面积,根据面积=边长×边长=边长的平方,已知斜边和一直角边的平方,由勾股定理可求出图中字母S所代表的正方形的面积.
【解答】解:Rt△ABC,∠ACB=90°,以三边为边长向外作正方形,64、400分别为所在正方形的面积,
400﹣64=336.
故图中字母S所代表的正方形面积是336.
故答案为:336.
15.【分析】分类讨论,①当5为直角边时,②当5为斜边时,依次求出答案即可.
【解答】解:①当5是直角边时,斜边=,此时第三边为;
②当5为斜边时,此时第三边=,
综上可得第三边的长度为4或.
故答案为:4或.
16.【分析】根据勾股定理可求AB,再根据垂线段最短可求CD⊥AB时,m+n有最大值.
【解答】解:∵△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB==5,
∵E、F分别为AD、BD中点,
∴EF=AB=2.5,
由垂线段最短可求CD⊥AB时,m+n有最大值2.5.
故答案为:2.5.
17.【分析】根据题意得到点C在以A为圆心,3为半径的圆上(不在直线AB上),当BC与圆A相切时,AC⊥BC,∠B取得最大值,然后根据勾股定理即可得到答案.
【解答】解:如图所示:
∵AC=3,
∴点C在以A为圆心,3为半径的圆上(不在直线AB上),
当BC与圆A相切时,AC⊥BC,∠B取得最大值,
∴BC===,
故答案为:.
18.【分析】分别在格点三角形中,根据勾股定理即可得到AB,BC,AC的长度,继而可得出∠ABC的度数.
【解答】解:
连接AC.
根据勾股定理可以得到:AC=BC=,AB=,
∵+=,即AC2+BC2=AB2,
∴△ABC是等腰直角三角形.
∴∠ABC=45°.
故答案为:45°.
19.【分析】设AE=ED=x,CD=y,根据勾股定理即可求出答案.
【解答】解:设AE=ED=x,CD=y,
∴BD=2y,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,
∴AB2=4x2+4y2,
∴x2+y2=1,
在Rt△CDE中,
∴EC2=x2+y2=1
∵EC>0
∴EC=1.
另解:依据AD⊥BC,BD=2CD,E是AD的中点,
即可得判定△CDE∽△BDA,
且相似比为1:2,
∴=,
即CE=1.
故答案为:1
20.【分析】过P作PD⊥OB,交OB于点D,在直角三角形POD中,利用锐角三角函数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据MN求出MD的长,由OD﹣MD即可求出OM的长.
【解答】解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,cos60°==,OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴OM=OD﹣MD=6﹣1=5.
故答案为:5.
21.【分析】本题考查直角三角形的性质及勾股定理,利用直角三角形的性质及勾股定理解答即可.
【解答】解:∵直角三角形的两直角边长分别为5cm和12cm
∴根据勾股定理斜边的长为:=13cm
∴三角形斜边上的中线的长为×13=6.5cm.
三.勾股定理的逆定理
22.【分析】先求得三角形的三边长,然后依据勾股定理的逆定理证明三角形为直角三角形,最后,再利用三角形的面积公式求解即可.
【解答】解:三角形的三边长分别为60×=10,60×=24,60×=26.
∵102+242=262,
∴三角形为直角三角形.
∴三角形的面积=×10×24=120.
故答案为:120.
23.【分析】先根据完全平方公式对已知等式进行化简,再根据勾股定理的逆定理进行判定.
【解答】解:∵(a+b)2=c2+2ab,
∴a2+2ab+b2﹣c2=2ab,
∴a2+b2=c2,
∴三角形是直角三角形.
故答案为直角三角形.
四.等腰直角三角形
24.【分析】作BE⊥AD于E,BF⊥CD于F,则四边形BEDF是矩形,证明△ABE≌△CBF(AAS),得出BE=BF,△ABE的面积=△CBF的面积,则四边形BEDF是正方形,四边形ABCD的面积=正方形BEDF的面积,求出BE=,则BD=BE=2
【解答】解:作BE⊥AD于E,BF⊥CD于F,如图所示:
则∠BEA=∠BFC=90°,
∵∠ADC=90°,
∴四边形BEDF是矩形,
∴∠EBF=90°,
∵∠ABC=90°,
∴∠EBF=∠ABC=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,,
∴△ABE≌△CBF(AAS),
∴BE=BF,△ABE的面积=△CBF的面积,
∴四边形BEDF是正方形,四边形ABCD的面积=正方形BEDF的面积,
∴BE=DE,BE2=10,
∴BE=,
∴BD=BE=2;
故答案为:2.
25.【分析】过E作EG⊥BC于G,过D作DF⊥BC交BC的延长线于F,得到四边形ABGE是矩形,求得BG=AE=,得到CG=6﹣=,根据全等三角形的性质得到DF=CG=,根据三角形的面积公式即可得到结论.
【解答】解:过E作EG⊥BC于G,过D作DF⊥BC交BC的延长线于F,
∵∠A=∠ABC=90°,
∴∠A=∠ABC=∠EGC=90°,
∴四边形ABGE是矩形,
∴BG=AE=,
∵BC=6,
∴CG=6﹣=,
∵CE⊥CD,
∴∠EGC=∠DFC=90°,
∴∠GEC+∠ECG=∠ECG+∠DCF=90°,
∵EC=CD,
∴△EGC≌△CFD(AAS),
∴DF=CG=,
∴△BCD的面积=BC?DF==.
故答案为:.
26.【分析】利用等腰三角形的性质分别求出∠ADB,∠BDC即可解决问题.
【解答】解:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BA=BD,
∵BA=BC,∠ABC=90°,
∴BD=BC,∠CBD=30°,
∴∠BDC=∠BCD=(180°﹣30°)=75°,
∴∠ADC=∠ADB+∠BDC=135°,
故答案为135.
27.【分析】作△ABC关于AC的对称△AEC,延长BD交AE于点F,则∠EAC=∠BAC,BC=EC,证出BF=AF,∠AFD=90°,证△BFE≌△AFD(AAS),得BE=AD=12,则BC=EC=6,由三角形面积公式即可得出答案.
【解答】解:作△ABC关于AC的对称△AEC,延长BD交AE于点F,如图所示:
则∠EAC=∠BAC,BC=EC,
∵∠ABD=2∠BAC=45°,
∴∠BAF=45°=∠ABD,
∴BF=AF,
∠AFD=90°,
∴BFE=90°,
∵∠EBF+∠E=∠DAF+∠E=90°,
∴∠EBF=∠DAF,
在△BFE和△AFD中,,
∴△BFE≌△AFD(AAS),
∴BE=AD=12,
∴BC=EC=6,
∴△ABD的面积=AD×BC=×12×6=36;
故答案为:36.
28.【分析】阴影部分的面积=外框大直角三角板的面积﹣内框小直角三角板的面积,根据等腰直角三角形的性质求出内框直角边长,再根据三角形面积公式计算即可求解.
【解答】解:如图,EF=DG=CH=,
∵含有45°角的直角三角板,
∴BC=,GH=2,
∴FG=6﹣﹣2﹣=4﹣2,
∴图中阴影部分的面积为:
×6×6﹣×(4﹣2)×(4﹣2)=18﹣12+8=6+8(cm2),
故答案为:(6+8).
29.【分析】给图中各角标上序号,由三角形外角的性质及对顶角相等可求出∠5的度数,由∠5的度数结合邻补角互补可求出∠3的度数,由直线a∥b利用“两直线平行,同位角相等”可得出∠2=∠3=80°,此题得解.
【解答】解:给图中各角标上序号,如图所示.
∵∠5=∠4+∠B,∠4=∠1=55°,∠B=45°,
∴∠5=45°+55°=100°.
∵∠3+∠5=180°,
∴∠3=80°.
∵直线a∥b,
∴∠2=∠3=80°.
故答案为:80°.
30.【分析】根据圆的定义,证明D、A、C、B四点共圆,可得∠ADF=45°,作高线AF,构建等腰直角△ADF和30度的直角△AFC,可以求得AF、DF、CF的长,利用三角形面积公式可得结论.
【解答】解:连接CE,
∵∠ACB=90°,E为AB的中点,
∴CE=AE=BE,
∵△ADE是等边三角形,
∴DE=AE,
∴DE=AE=CE=BE,
∴D、A、C、B在以点E为圆心的圆上,作⊙E,
∴∠ADC=∠ABC=45°,
过A作AF⊥CD于F,
∴△ADF是等腰直角三角形,
∵AD=AE=AB=2,
∴AF=DF==,
∵∠CAF=∠DAB+∠BAC﹣∠DAF=60°+45°﹣45°=60°,
∴∠ACF=30°,
∴AC=2AF=2,
由勾股定理得:CF===,
∴S△ADC=CD?AF=(+)×=1+,
故答案为:1.
31.【分析】由等腰直角三角形的性质可用BC把DE2表示出来,再利用二次函数的性质可求得答案.
【解答】解:
在等腰RT△ACD和等腰RT△CBE中AD=CD,CE=BE,∠ACD=∠A=45°,∠ECB=∠B=45°
∴∠DCE=90°
∴AD2+CD2=AC2,CE2+BE2=CB2
∴CD2=AC2,CE2=CB2,
∴DE2=DC2+EC2=AC2+CB2=(AC+BC)2﹣AC?BC=﹣BC(5﹣BC)=BC2﹣5BC+=(BC﹣)2+,
∴当CB=时,DE2有最小值的值最小,
即x2+y2的最小值为,
故答案为:.
32.【分析】设AO=a,解直角三角形,求出每个等腰直角三角形的斜边长,再证相似,根据相似三角形的性质即可求出答案.
【解答】解:设AO=a,
∵AB=OB,∠ABO=90°,
∴∠BOA=45°,
∴BO=AO×cos45°=AO=a,
同理CO=BO=()2a,
DO=()3a,
EO=()4a,
FO=()5a,
GO=()6a,
HO=()7a,
∵△OAB和△OHI都是等腰三角形,
∴两三角形相似,
∵OH:OA=()7
∴△OAB与△OHI面积的比是()2=[()7]2=128,
故答案为:128.
1
一.直角三角形的性质
1.(2016春?工业园区期中)如图,已知点P是射线ON上一动点(即P可在射线ON上运动),∠AON=30°,当∠A=
时,△AOP为直角三角形.
二.勾股定理
2.(2020春?相城区期末)如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当AD平分∠BAC时,AP的长为
.
3.(2019秋?太仓市期末)如图示,在Rt△ABC中,∠ACB=90°,AC=3,BC=,点P在Rt△ABC内部,且∠PAB=∠PBC,连接CP,则CP的最小值等于
.
4.(2017秋?苏州期末)在如图所示的“勾股树”中,已知正方形内的数字或字母表示该正方形的边长,由此可以计算:m2+n2=
.
5.(2017秋?常熟市期末)如图,在Rt△ABC中,∠C=90°,点D是边BC上的一点,∠CAD=30°,BD=2,AB=,则CD的长为
.
6.(2017秋?吴江区期末)我国古代把直角三角形较短的直角边称为
.
7.(2017秋?吴江区期末)如图,方格中小正方形的边长为1,△ABC的三个顶点和线段EF的两个端点都在小正方形的格点(顶点)上,小明在观察探究时得到以下四个结论:
①△ABC是等边三角形;②△ABC的周长是;
③△ABC的面积是4;④直线EF是线段BC的垂直平分线.
你认为以上结论中,正确的序号有
.
8.(2019秋?苏州期中)如图,以Rt△ABC的两条直角边为边长向外作正方形S1,S2,若AB=2,则正方形S1,S2的面积和为
.
9.(2018秋?吴江区期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=32,AB=40,且BD:DC=5:3.则△ADB的面积为
.
10.(2017秋?相城区期中)如图,在Rt△ABC中∠B=90°,AC=25,BC=15,以AC,BC为直径的半圆的面积分别为S1,S2,则S1﹣S2=
.(结果保留π)
11.(2017秋?张家港市校级期中)若等腰三角形中腰长为10cm,第三边长为16cm,那么第三边上的高为
.
12.(2017秋?太仓市校级期中)如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD2=
.
13.(2017秋?太仓市期中)在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,a=5,b=12,则c=
.
14.(2016秋?虎丘区校级期中)如图,Rt△ABC,∠ACB=90°,以三边为边长向外作正方形,64、400分别为所在正方形的面积,则图中字母S所代表的正方形面积是
.
15.(2016秋?吴中区期中)已知直角三角形的两边长为3cm、5cm,则它的第三边长为
.
16.(2020?姑苏区一模)如图,△ABC中,∠ACB=90°,AC=4,BC=3,射线CD与边AB交于点D,E、F分别为AD、BD中点,设点E、F到射线CD的距离分别为m、n,则m+n的最大值为
.
17.(2017?太仓市模拟)已知△ABC中,AB=4,AC=3,当∠B取得最大值时,BC的长度为
.
18.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,连接AB、BC,则∠ABC的度数为
.
19.(2020?苏州)如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC=
.
20.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
.
21.已知直角三角形的两直角边长分别为5cm和12cm,则此直角三角形斜边上的中线的长为
cm.
三.勾股定理的逆定理
22.(2017秋?高新区期末)一个三角形的三边长之比是5:12:13,且周长是60,则它的面积是
.
23.(2016秋?吴江区期中)三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是
.
四.等腰直角三角形
24.(2020春?工业园区期末)如图,四边形纸片ABCD中,AB=BC,∠ABC=∠ADC=90°.若该纸片的面积为10cm2,则对角线BD=
cm.
25.(2020春?常熟市期末)如图,在五边形ABCDE中,∠A=∠ABC=90°,AE=,BC=6,连接CE,BD.若CE⊥CD且CE=CD,则△BCD的面积为
.
26.(2018秋?苏州期末)如图,△ABC为等腰直角三角形,∠ABC=90°,△ADB为等边三角形,则∠ADC=
°.
27.(2019秋?苏州期中)如图,△ABC中,∠C=90°,点D为AC上一点,∠ABD=2∠BAC=45°,若AD=12,则△ABD的面积为
.
28.(2019秋?苏州期中)如图,一块含有45°角的直角三角板,外框的一条直角边长为6cm,三角板的外框线和与其平行的内框线之间的距离均为cm,则图中阴影部分的面积为
cm2(结果保留根号).
29.(2019?张家港市模拟)已知直线a∥b,将一块含45°角的直角三角板(∠C=90°),按如图所示的位置摆放,若∠1=55°,则∠2的度数为
.
30.(2018?昆山市一模)如图,在等腰Rt△ABC中,∠ACB=90°,AB=4,点E为AB的中点.以AE为边作等边△ADE(点D与点C分别在AB的异侧),连接CD.则△ACD的面积为
.
31.(2016?苏州二模)如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是
.
32.如图,以OA为斜边作等腰Rt△OAB,再以OB为斜边在△OAB外侧作等腰Rt△OBC,如此继续,得到8个等腰直角三角形,则△OAB与△OHI面积的比值是
.
答案与解析
一.直角三角形的性质
1.【分析】根据点P的运动轨迹,分∠APO是直角和锐角两种情况讨论求解.
【解答】解:若∠APO是直角,则∠A=90°﹣∠AON=90°﹣30°=60°,
若∠APO是锐角,∵∠AON=30°是锐角,
∴∠A=90°,
综上所述,∠A=60°或90°.
故答案为:60°或90°.
二.勾股定理(共20小题)
2.【分析】根据勾股定理求出AC,根据角平分线的定义、平行线的性质得到∠ADP=∠PAD,得到PA=PD,根据相似三角形的性质列出比例式,计算即可.
【解答】解:∵∠C=90°,AB=5,BC=4,
∴AC==3,
∵PQ∥AB,
∴∠BAD=∠ADP,
又∵AD平分∠BAC,
∴∠BAD=∠PAD,
∴∠ADP=∠PAD,
∴PA=PD,
∴QP=2PA,
∵PQ∥AB,
∴△CPQ∽△CAB,
∴=,即=,
解得PA=.
故答案为:.
3.【分析】构造点P在以AB为弦的圆上,首先求得∠APB=120°,然后求得半径和OC的长,当点O、P、C在一条直线上时,CP有最小值.
【解答】解:如图所示,
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=,
∴tan∠BAC==,
∴∠BAC=30°,
∴∠CBA=60°,即∠1+∠2=60°,
∵∠PAB=∠1,
∴∠PAB+∠2=60°,
∴∠APB=120°,
∴点P在以AB为弦的圆O上,
∴∠AOB=120°,
∵OA=OB,
∴∠3=∠4=30°,
∴∠1+∠2+∠3=90°,即∠CBO=90°,
∠DAO=∠BAC+∠4=60°,∠AOD=30°,
过点O作OD⊥AC于点D,
∴∠DOB=90°,
∵∠DCB=90°,
∴四边形DCBO是矩形,
∴DC=OB,OD=BC=,
∴在Rt△ADO中,AD=OD?tan30°=×=1,
∴DC=AC﹣DC=3﹣1=2,
∴OB=OP=2,
∴OC===,
当点O、P、C在一条直线上时,CP有最小值,
∴CP的最小值为OC﹣OP=﹣2.
故答案为﹣2.
4.【分析】根据勾股定理和正方形的面积公式解答.
【解答】解:如图,m2=a2﹣42,n2=b2﹣32,a2+b2=62
则m2+n2=a2﹣42+b2﹣32=62﹣42﹣32=11.
故答案是:11.
5.【分析】设CD=x,根据直角三角形的性质用x表示出AD,根据勾股定理求出AC,再根据勾股定理列方程,解方程得到答案.
【解答】解:设CD=x,
∵∠C=90°,∠CAD=30°,
∴AD=2CD=2x,
由勾股定理得,AC==x,
则(x)2+(x+2)2=12
解得,x1=1,x2=﹣2(舍去)
故答案为:1.
6.【分析】根据勾股定理的概念解答即可.
【解答】解:我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦,
故答案为:勾
7.【分析】根据勾股定理求出AC、BC、AB长,即可判断①和②,求出AC边上的高,即可判断③,证△MTD≌△BZC,推出∠ZBC=∠TMD,能求出EF⊥BC,根据等腰三角形性质即可求出CO=BO,即可判断④.
【解答】解:∵由勾股定理得:AB=,AC=,BC=,
∴AB=BC,
∴△ABC的形状是等腰三角形,∴①错误;
△ABC的周长是++2=2+2,∴②正确;
连接BN,由勾股定理得:AN=CN,
在△BCN和△BAN中
∴△BCN≌△BAN,
∴∠BNC=∠BNA,
∵∠BNC+∠BNA=180°,
∴∠BNC=90°,
由勾股定理得:BN=,
∴△ABC的面积是AC×BN=×2×2=4,∴③正确;
在△MTD和△BZC中
∴△MTD≌△BZC,
∴∠ZBC=∠TMD,
∵∠MTD=90°,
∴∠TDM+∠TMD=∠ZBC+∠BRO=90°,
∴∠ROB=90°,
∴EF⊥BC,
由勾股定理得:BM=CM,
∴CO=BO,
直线EF是线段BC的垂直平分线,∴④正确;
故答案为:②③④.
8.【分析】根据正方形的面积公式和勾股定理得到正方形S1,S2的面积和是斜边AB的平方.
【解答】解:∵以Rt△ABC的两条直角边为边长向外作正方形S1,S2,
∴正方形S1的面积是AC2,正方形S2的面积是BC2,AC2+BC2=AB2,
∴正方形S1,S2的面积和为:AC2+BC2=AB2=22=4.
故答案是:4.
9.【分析】作DE⊥AB于E,根据角平分线的性质得到DE=DC,再由BC=32,BD:DC=5:3,CD=×32=12,则DE=12,然后根据三角形面积公式计算即可.
【解答】解:作DE⊥AB于E,如图,
∵∠C=90°,AD平分∠BAC,
∴DE=DC,
∵BC=32,BD:DC=5:3,
∴CD=×32=12,
∴DE=12,
∴△ADB的面积=AB?DE=×40×12=240.
故答案为:240.
10.【分析】根据半圆面积公式,求出S1、S2即可解决问题.
【解答】解:S1=π()2=πAC2=π,S2=πBC2=π,
所以S1﹣S2=50π.
11.【分析】根据等腰三角形的性质先求出BD,然后在RT△ABD中,可根据勾股定理进行求解.
【解答】解:如图:
由题意得:AB=AC=10cm,BC=16cm,
作AD⊥BC于点D,则有DB=BC=8cm,
在Rt△ABD中,AD==6cm.
故答案为:6cm.
12.【分析】根据等式的性质,可得∠BAD与∠CAD′的关系,根据SAS,可得△BAD与△CAD′的关系,根据全等三角形的性质,可得BD与CD′的关系,根据勾股定理,可得答案.
【解答】解:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:
∵∠BAC+∠CAD=∠DAD′+∠CAD,
即∠BAD=∠CAD′,
在△BAD与△CAD′中,
,
∴△BAD≌△CAD′(SAS),
∴BD=CD′.
∠DAD′=90°
由勾股定理得DD′=,
∠D′DA+∠ADC=90°,
由勾股定理得CD′=,
∴BD=CD′=,即BD2=41.
故答案为:41.
13.【分析】在Rt△ABC中,利用勾股定理可求出c的长度即可.
【解答】解:因为在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,a=5,b=12,
所以c===13,
故答案为:13.
14.【分析】要求图中字母S所代表的正方形面积,根据面积=边长×边长=边长的平方,已知斜边和一直角边的平方,由勾股定理可求出图中字母S所代表的正方形的面积.
【解答】解:Rt△ABC,∠ACB=90°,以三边为边长向外作正方形,64、400分别为所在正方形的面积,
400﹣64=336.
故图中字母S所代表的正方形面积是336.
故答案为:336.
15.【分析】分类讨论,①当5为直角边时,②当5为斜边时,依次求出答案即可.
【解答】解:①当5是直角边时,斜边=,此时第三边为;
②当5为斜边时,此时第三边=,
综上可得第三边的长度为4或.
故答案为:4或.
16.【分析】根据勾股定理可求AB,再根据垂线段最短可求CD⊥AB时,m+n有最大值.
【解答】解:∵△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB==5,
∵E、F分别为AD、BD中点,
∴EF=AB=2.5,
由垂线段最短可求CD⊥AB时,m+n有最大值2.5.
故答案为:2.5.
17.【分析】根据题意得到点C在以A为圆心,3为半径的圆上(不在直线AB上),当BC与圆A相切时,AC⊥BC,∠B取得最大值,然后根据勾股定理即可得到答案.
【解答】解:如图所示:
∵AC=3,
∴点C在以A为圆心,3为半径的圆上(不在直线AB上),
当BC与圆A相切时,AC⊥BC,∠B取得最大值,
∴BC===,
故答案为:.
18.【分析】分别在格点三角形中,根据勾股定理即可得到AB,BC,AC的长度,继而可得出∠ABC的度数.
【解答】解:
连接AC.
根据勾股定理可以得到:AC=BC=,AB=,
∵+=,即AC2+BC2=AB2,
∴△ABC是等腰直角三角形.
∴∠ABC=45°.
故答案为:45°.
19.【分析】设AE=ED=x,CD=y,根据勾股定理即可求出答案.
【解答】解:设AE=ED=x,CD=y,
∴BD=2y,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,
∴AB2=4x2+4y2,
∴x2+y2=1,
在Rt△CDE中,
∴EC2=x2+y2=1
∵EC>0
∴EC=1.
另解:依据AD⊥BC,BD=2CD,E是AD的中点,
即可得判定△CDE∽△BDA,
且相似比为1:2,
∴=,
即CE=1.
故答案为:1
20.【分析】过P作PD⊥OB,交OB于点D,在直角三角形POD中,利用锐角三角函数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据MN求出MD的长,由OD﹣MD即可求出OM的长.
【解答】解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,cos60°==,OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=MN=1,
∴OM=OD﹣MD=6﹣1=5.
故答案为:5.
21.【分析】本题考查直角三角形的性质及勾股定理,利用直角三角形的性质及勾股定理解答即可.
【解答】解:∵直角三角形的两直角边长分别为5cm和12cm
∴根据勾股定理斜边的长为:=13cm
∴三角形斜边上的中线的长为×13=6.5cm.
三.勾股定理的逆定理
22.【分析】先求得三角形的三边长,然后依据勾股定理的逆定理证明三角形为直角三角形,最后,再利用三角形的面积公式求解即可.
【解答】解:三角形的三边长分别为60×=10,60×=24,60×=26.
∵102+242=262,
∴三角形为直角三角形.
∴三角形的面积=×10×24=120.
故答案为:120.
23.【分析】先根据完全平方公式对已知等式进行化简,再根据勾股定理的逆定理进行判定.
【解答】解:∵(a+b)2=c2+2ab,
∴a2+2ab+b2﹣c2=2ab,
∴a2+b2=c2,
∴三角形是直角三角形.
故答案为直角三角形.
四.等腰直角三角形
24.【分析】作BE⊥AD于E,BF⊥CD于F,则四边形BEDF是矩形,证明△ABE≌△CBF(AAS),得出BE=BF,△ABE的面积=△CBF的面积,则四边形BEDF是正方形,四边形ABCD的面积=正方形BEDF的面积,求出BE=,则BD=BE=2
【解答】解:作BE⊥AD于E,BF⊥CD于F,如图所示:
则∠BEA=∠BFC=90°,
∵∠ADC=90°,
∴四边形BEDF是矩形,
∴∠EBF=90°,
∵∠ABC=90°,
∴∠EBF=∠ABC=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,,
∴△ABE≌△CBF(AAS),
∴BE=BF,△ABE的面积=△CBF的面积,
∴四边形BEDF是正方形,四边形ABCD的面积=正方形BEDF的面积,
∴BE=DE,BE2=10,
∴BE=,
∴BD=BE=2;
故答案为:2.
25.【分析】过E作EG⊥BC于G,过D作DF⊥BC交BC的延长线于F,得到四边形ABGE是矩形,求得BG=AE=,得到CG=6﹣=,根据全等三角形的性质得到DF=CG=,根据三角形的面积公式即可得到结论.
【解答】解:过E作EG⊥BC于G,过D作DF⊥BC交BC的延长线于F,
∵∠A=∠ABC=90°,
∴∠A=∠ABC=∠EGC=90°,
∴四边形ABGE是矩形,
∴BG=AE=,
∵BC=6,
∴CG=6﹣=,
∵CE⊥CD,
∴∠EGC=∠DFC=90°,
∴∠GEC+∠ECG=∠ECG+∠DCF=90°,
∵EC=CD,
∴△EGC≌△CFD(AAS),
∴DF=CG=,
∴△BCD的面积=BC?DF==.
故答案为:.
26.【分析】利用等腰三角形的性质分别求出∠ADB,∠BDC即可解决问题.
【解答】解:∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BA=BD,
∵BA=BC,∠ABC=90°,
∴BD=BC,∠CBD=30°,
∴∠BDC=∠BCD=(180°﹣30°)=75°,
∴∠ADC=∠ADB+∠BDC=135°,
故答案为135.
27.【分析】作△ABC关于AC的对称△AEC,延长BD交AE于点F,则∠EAC=∠BAC,BC=EC,证出BF=AF,∠AFD=90°,证△BFE≌△AFD(AAS),得BE=AD=12,则BC=EC=6,由三角形面积公式即可得出答案.
【解答】解:作△ABC关于AC的对称△AEC,延长BD交AE于点F,如图所示:
则∠EAC=∠BAC,BC=EC,
∵∠ABD=2∠BAC=45°,
∴∠BAF=45°=∠ABD,
∴BF=AF,
∠AFD=90°,
∴BFE=90°,
∵∠EBF+∠E=∠DAF+∠E=90°,
∴∠EBF=∠DAF,
在△BFE和△AFD中,,
∴△BFE≌△AFD(AAS),
∴BE=AD=12,
∴BC=EC=6,
∴△ABD的面积=AD×BC=×12×6=36;
故答案为:36.
28.【分析】阴影部分的面积=外框大直角三角板的面积﹣内框小直角三角板的面积,根据等腰直角三角形的性质求出内框直角边长,再根据三角形面积公式计算即可求解.
【解答】解:如图,EF=DG=CH=,
∵含有45°角的直角三角板,
∴BC=,GH=2,
∴FG=6﹣﹣2﹣=4﹣2,
∴图中阴影部分的面积为:
×6×6﹣×(4﹣2)×(4﹣2)=18﹣12+8=6+8(cm2),
故答案为:(6+8).
29.【分析】给图中各角标上序号,由三角形外角的性质及对顶角相等可求出∠5的度数,由∠5的度数结合邻补角互补可求出∠3的度数,由直线a∥b利用“两直线平行,同位角相等”可得出∠2=∠3=80°,此题得解.
【解答】解:给图中各角标上序号,如图所示.
∵∠5=∠4+∠B,∠4=∠1=55°,∠B=45°,
∴∠5=45°+55°=100°.
∵∠3+∠5=180°,
∴∠3=80°.
∵直线a∥b,
∴∠2=∠3=80°.
故答案为:80°.
30.【分析】根据圆的定义,证明D、A、C、B四点共圆,可得∠ADF=45°,作高线AF,构建等腰直角△ADF和30度的直角△AFC,可以求得AF、DF、CF的长,利用三角形面积公式可得结论.
【解答】解:连接CE,
∵∠ACB=90°,E为AB的中点,
∴CE=AE=BE,
∵△ADE是等边三角形,
∴DE=AE,
∴DE=AE=CE=BE,
∴D、A、C、B在以点E为圆心的圆上,作⊙E,
∴∠ADC=∠ABC=45°,
过A作AF⊥CD于F,
∴△ADF是等腰直角三角形,
∵AD=AE=AB=2,
∴AF=DF==,
∵∠CAF=∠DAB+∠BAC﹣∠DAF=60°+45°﹣45°=60°,
∴∠ACF=30°,
∴AC=2AF=2,
由勾股定理得:CF===,
∴S△ADC=CD?AF=(+)×=1+,
故答案为:1.
31.【分析】由等腰直角三角形的性质可用BC把DE2表示出来,再利用二次函数的性质可求得答案.
【解答】解:
在等腰RT△ACD和等腰RT△CBE中AD=CD,CE=BE,∠ACD=∠A=45°,∠ECB=∠B=45°
∴∠DCE=90°
∴AD2+CD2=AC2,CE2+BE2=CB2
∴CD2=AC2,CE2=CB2,
∴DE2=DC2+EC2=AC2+CB2=(AC+BC)2﹣AC?BC=﹣BC(5﹣BC)=BC2﹣5BC+=(BC﹣)2+,
∴当CB=时,DE2有最小值的值最小,
即x2+y2的最小值为,
故答案为:.
32.【分析】设AO=a,解直角三角形,求出每个等腰直角三角形的斜边长,再证相似,根据相似三角形的性质即可求出答案.
【解答】解:设AO=a,
∵AB=OB,∠ABO=90°,
∴∠BOA=45°,
∴BO=AO×cos45°=AO=a,
同理CO=BO=()2a,
DO=()3a,
EO=()4a,
FO=()5a,
GO=()6a,
HO=()7a,
∵△OAB和△OHI都是等腰三角形,
∴两三角形相似,
∵OH:OA=()7
∴△OAB与△OHI面积的比是()2=[()7]2=128,
故答案为:128.
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
