人教版小学数学六年级下册讲义 圆柱的表面积和体积的综合练习(含答案)
文档属性
| 名称 | 人教版小学数学六年级下册讲义 圆柱的表面积和体积的综合练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 129.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 00:00:00 | ||
图片预览




文档简介
圆柱的表面积和体积的综合练习
学生姓名
年级
学科
授课教师
日期
时段
核心内容
掌握圆柱的表面积和体积的计算
课型
一对一/一对N
教学目标
1、理解圆柱表面积意义,掌握体积公式的推导方法。
2、能够灵活运用公式计算圆柱的表面积与体积。
3、掌握圆柱体的切割类型题目。
重、难点
重点:教学目标1、2 难点:教学目标3
2532894114886
课首沟通
了解学生对圆柱体表面积以及体积的掌握情况。
知识导图
36830090319
课首小测
两个圆柱体的侧面积相等,它们的体积一定相等。( )
两个圆柱底面积和高分别相等,它们的体积也相等。( )
如果两个圆柱的体积相等,那么它们的底面积和高分别相等。( )
一个圆柱体和一个长方体高相等,底面周长相等,它们的体积也相等。( )
圆柱体底面积和高都扩大2倍,体积就扩大4倍。( )
[单选题] 圆柱体的底面半径和高都扩大2倍,它的体积扩大( )倍。
A.2 B.4 C.6 D.8
[单选题] 等底等高的圆柱体、正方体、长方体的体积相比较,( )。
A.正方体体积大 B.长方体体积大 C.圆柱体体积大 D.一样大
8. [单选题]
圆柱体的底面半径扩大3倍,高不变,体积扩大(
)。
A.3倍
B.9倍
C.6倍
9. [单选题] 求长方体、正方体、圆柱体的体积共同的公式是( )。
A.V=abh B.V= C.V=Sh 10. [单选题] 压路机的前轮转动一圈能压多少路面是指( )。
A.前轮的两个圆的面积 B.前轮的表面积 C.前轮的周长 D.前轮的侧面积
11. [单选题] 把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?
( )。
A.表面积和体积都没变 B.表面积和体积都发生了变化
C.表面积变了,体积没变 D.表面积没变,体积变了
2532894143560
导学一 : 圆柱表面积和体积求解的特殊类型
知识点讲解 1:求圆柱体表面积的特殊类型
侧面积:圆柱的侧面展开是一个长方形或正方形,长方形的长等于圆柱的底面周长(C=2πr=(d),宽等于圆柱的高。 S侧 =Ch =2πr h=πdh
侧面积公式的应用:
①已知C和h,求S侧; ②已知d和h,求S侧; ③已知r和h,求S侧。表面积: S表 = S侧+2S底=Ch+2πr?
表面积公式的应用:
①求一个底面积和侧面积(无盖的桶、茶杯、水池等);②只求侧面积(压路机、排水管、烟囱、通风管等)。
368300228907例 1. 如下图,高都是10厘米,底面半径分别是3厘米、6厘米的两个圆柱组成了一个几何体。求这个物体的表面积。
6131302237469例 2. 在一个棱长4厘米的正方体的六个面各中心挖去一个底面半径为1厘米,深1厘米的圆柱,求它的表面积。
例 3. 有一张长方形铁皮如图所示,剪下阴影部分制成圆柱体(单位:厘米),求这个圆柱体的表面积。(提示:圆桶盖的周长等于长方形铁皮的长)
我爱展示
圆柱的高都是1米,底面半径分别是1米、2米和3米。求这个物体的表面积。
36830093470
368300454904有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的直孔,如下图.圆孔的直径是4厘 米,孔深5厘米.如果将这个零件接触空气部分涂上防锈漆,一共需涂多少平方厘米?
377550200261把一张铁皮如图所示剪开,正好能制成一只铁皮汽油桶,求所制汽油桶的表面积。
知识点讲解 2:求圆柱体体积的特殊类型
体积: V柱=S底h=πr?h 圆柱体积公式的应用:
①已知S底和h,求V;②已知r和h,求V;③已知d和h,求V;④已知C和h,求V。
例 1. 一个圆柱体的体积是640立方厘米,底面积是80平方厘米,它的高是多少厘米?
例 2. 把一块长10厘米,宽1.57厘米,高10厘米的长方体橡皮泥,捏成直径是2厘米的圆橡皮泥条,橡皮泥条长多少厘米?
例 3. 把棱长是8厘米的正方体木块,削成一个最大的圆柱,圆柱体的体积是多少?
例 4. 一只钢管,长100厘米,外直径20厘米,内直径是16厘米,每立方厘米钢重8.2克,这只钢管重多少千克?
例 5. 有一个圆柱形水桶,底面直径2分米,盛水未满,放入一个铁球,当铁球完全沉入水中之后,水面升高3厘米,求铁球的体积?
我爱展示
一个圆柱体的侧面积是12.56平方分米,高2分米,它体积是( )。
一个圆柱形粮囤的底面周长是9.42米,高是2米,每立方米小麦重800千克,这个粮囤能装小麦多少千克?
一个长方体,长8分米,宽8分米,高12分米。把它削成一个最大的圆柱,这个圆柱的体积为多少立方分米?
一个圆柱形水槽,底面半径是8厘米,水槽中完全浸没着一块铁件,当铁件取出时,水面下降了5厘米。这块铁件的体 积是多少立方厘米?
导学二 : 圆柱体切割
知识点讲解 1:圆柱体切割与表面积的联系
① 圆柱的切割变化时,注意比较观察增加(减少)的面;
② 确定已知条件、未知条件,检查单位是否统一,正确选用公式计算。
例 1. 把高10厘米的圆柱体按下图切开,拼成近似的长方体,表面积就增加了40平方厘米,这个圆柱体的底面半径是
( )厘米,体积是( )立方厘米。
例 2. 一个圆柱体,如果把它的高截短2厘米,表面积就减少62.8平方厘米,那么它的体积就减少多少立方厘米?
我爱展示
368300403242将一根长1米圆柱形木条截成三段小圆柱形木条,表面积增加4平方分米,这根圆柱形木条原来的体积是多少立方分 米?
371805193901将一根长1米,底面半径为3分米的圆柱体木料,沿着底面直径劈开,表面积增加了多少平方分米?
一个圆柱体,如果把它的高增加2厘米,表面积就增加37.68平方厘米,那么这个圆柱体的体积增加了多少立方厘米?
2532894130072
限时考场模拟 : 15分钟
(2014年大联盟小升初真题)一个圆柱体的侧面展开图是一个正方形,此圆柱底面直径与高的比是1:π。( )
一个圆柱的底面周长是6.28分米,高2分米,它的侧面积是( )平方分米,表面积是( )平方分米,体积是( )立方分米。
用一张长4分米,宽2分米的长方形纸,围成一个圆柱形纸筒,它的侧面积是( )平方分米。
(2014年天河区小学毕业考试题)如图,将这个长方形绕轴旋转一周,得到的立体图形是( ),它的体积是( )cm?。
一根长4米,横截面半径为2分米的圆柱形木料截成同样长的4段,表面积比原来增加( )平方分米。
372871194799一个圆柱形水池,水池内壁和底面都要镶上瓷砖,水池底面直径6米,池深1.2米。镶瓷砖的面积是多少平方米?
368300412166某种饮料罐的形状为圆柱形,底面直径是7cm,高是12cm。将24罐这种饮料按如图所示的方式放入箱内,这个纸箱的 长、宽、高至少各是多少厘米?
课后作业
1. [单选题]
A.侧面积
一只铁皮水桶能装多少升水是求水桶的(
B.表面积
)。
C.容积
D.体积
[单选题] 做一只圆柱形的油桶,至少要用多少铁皮,是求油桶的( )。
A.侧面积 B.表面积 C.容积 D.体积
[单选题] 做一节圆柱形铁皮通风管要用多少铁皮,是求通风管的( )。
A.侧面积 B.表面积 C.容积 D.体积
[单选题] 求一段圆柱形钢条有多少立方米,是求钢条的( )。
A.侧面积 B.表面积 C.容积 D.体积
[单选题] 把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A.50.24 B.100.48 C.64
(2013年大联盟小升初真题)做一个圆柱形的笔筒,底面半径是4厘米,高是10厘米,做这个笔筒至少需要(
)平方厘米的铁皮。(保留整数)
一个圆柱形油桶,侧面展开是一个正方形,已知这个油桶的底面半径是10厘米,那么油桶的高是( )厘米。
(2011年天河区小学毕业考试题)一根圆柱形木料底面周长是12.56分米,高是6米。如果把它截成四段小圆柱,需要 截( )次,表面积增加( )平方分米。
把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体,表面积比原来增加了200平方厘米。已知 圆柱高20厘米,圆柱的体积是( )立方厘米。
(2010年天河区小学毕业考试题)一台压路机的前轮是圆柱形,轮宽2米,半径0.5米。前轮转动10周,压路的面积 是多少平方米?
(2010年大联盟小升初试题)把一块底面直径8分米、高6分米的圆柱体铜块熔铸成一个长方体,这个长方体长4分 米、宽2分米,它的高是多少分米?
一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米。做这个水桶要用铁皮多少平方厘米?(得数保留 整百平方厘米)这个水桶可以盛水多少千克?(每升水重1千克)
有一根圆柱形的木棒,直径是10厘米,高是20厘米,沿着直径锯成相等的两块,每块的表面积是多少?每块的体积 是多少?
一个圆柱形水池,从里面量底面周长是12.56米,深4米,如果在池底和池壁抹一层水泥,每平方米使用水泥0.8千 克,需要水泥多少千克?这个水池的占地面积是多少?这个水池可以盛水多少升?
有一个高是10厘米的圆柱,如果它的高减少2厘米,表面积就减少18.84平方厘米,原来圆柱的体积是多少立方厘 米?
压路机的前轮是圆柱,底面直径是1米,长是1.5米,从一条公路的一端压到另一端,共滚动了450周,这条公路有多 长?压过的路面有多少平方米?
一种圆柱形的奶粉盒底面周长是37.68厘米,高15厘米,如果装在长3分米、宽3.6分米、高2.4分米的长方体纸箱 内,每箱最多可以装多少盒奶粉?
2532894241365
1、课后先复习本节课的内容;
2、认真完成本堂课的课后作业;
3、本堂课中的错题誊写到错题本上,下节课会对错题进行练习。
2532894212031
课首小测
1.错
解析:因为把同一个长方形可以卷成体积不同的两个圆柱体,所以体积也相等是错误的表述。2.对
解析:根据公式V=Sh,可知它们的体积也相等。3.错
解析:圆柱的体积是V=Sh,S=π r?,所以V=π r?h,V相等,r和h的组合很多,并不一定是它们的底面积和高分别相等 ,所以是错误的。
4.错
解析:底面周长相等的情况下,圆的底面积最大,所以体积应该是圆柱体较大。5.对
解析:根据公式V=Sh,可知体积扩大4倍。6.D
解析:根据公式V=π r?h,可知体积应扩大8倍。7.D
解析:根据公式V=Sh,可知它们的体积也相等。8.B
解析:根据公式V=πr?h,可知体积应扩大9倍。9.C
解析:根据公式V=Sh,都可以分别求出这三个立方体的体积。10.D
解析: 表面积的实际应用,结合生活实际情况,与地面接触的是圆柱体的侧面积。11.C
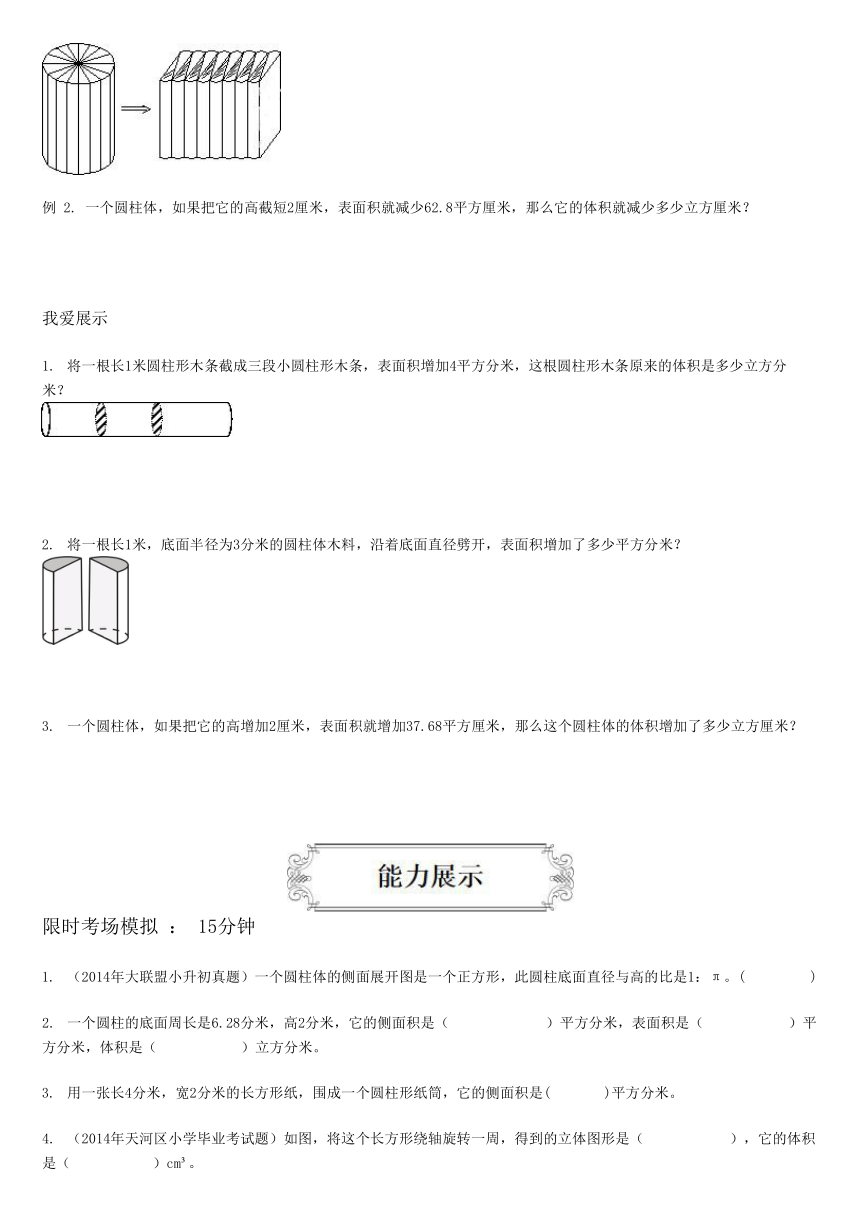
解析:把圆柱体切拼成长方体,这是书本圆柱体体积的推导方法,表面积会变化,体积依然没有变。
导学一
知识点讲解 1:求圆柱体表面积的特殊类型例题
1.791.28平方厘米
解析:图中几何体是由2个圆柱体组成,分别求出两个圆柱体侧面展开图的面积,大圆柱体的两个底面面积,两部分面积 相加即可求出该物体的表面积。
列式:2×3.14×3×10+2×3.14×6×10+3.14×6?×2
=3.14×(60+120+72)
=791.28(平方厘米) 2.133.68平方厘米
解析:这个物体的表面积是棱长为4厘米的正方体的面积,加上6个底面半径为1厘米、高1厘米的的小圆柱体的侧面积,据 此解答即可。
列式:4×4×6+3.14×1×2×1×6=96+37.68=133.68(平方厘米)
3.131.88平方厘米
解析:观察图形可知,组成这个圆柱体的底面积周长为18.84厘米,利用公式C=πd求出圆柱体底面直径d,圆柱体高为10 减去直径d,圆柱体表面积=阴影长方形面积+两个圆面积。
圆柱的底面直径是:18.84÷3.14=6(厘米); 圆柱体的高是:10-6=4(厘米);
圆柱体表面积是:18.84×4+3.14×(6÷2)?×2=131.88(平方厘米)。答:略。
我爱展示
1.94.2平方米
解析:分别求出图中三个圆柱体的侧面展开图的面积,之后求出最大圆柱体的两个底面面积,两部分相加即可求出这个物 体的表面积。
列式:3.14×3?×2+3.14×(1×2+2×2+3×2)×1=94.2(平方米)
答 : 略 。 2.307.72平方厘米
解析:涂漆的面积是:3.14×(6÷2)?×2+3.14×6×10+3.14×4×5=307.72(平方厘米) 答:略。
3.31.4平方分米
解析:观察图形可知,组成的这个圆柱的高为两个圆的直径,底面周长为直径加上圆形周长。汽油桶底面直径:8.28÷(3.14+1)=2(分米)
汽油桶表面积:3.14×(2÷2)?×2+(8.28-2)×2×2=31.4(平方分米)
知识点讲解 2:求圆柱体体积的特殊类型例题
1.8厘米
解析:640÷80=8(厘米) 答:略。
2.50厘米
解析:长方体的体积:10×1.57×10=157(立方厘米); 橡皮泥条底面积: 3.14×(2÷2)?=3.14(平方厘米); 橡皮泥条长:157÷3.14=50(厘米)
3.401.92立方厘米
解析:要使圆柱体最大,正方体的棱长是圆柱体底面直径,根据体积公式即可求出答案。列式:3.14×(8÷2)?×8=401.92(立方厘米)
4.926.928千克
解析:钢管的体积=直径为20厘米的圆柱体体积-直径为16厘米的圆柱体体积。钢管的体积为:3.14×[(20÷2)?-(16÷2)?]×100=11304(立方厘米); 钢管重为:11304×8.2=92692.8(克);92692.8克=92.6928千克
答 : 略 。 5.942立方厘米
解析:铁球体积为水面升高后增加的体积。
列式:2分米=20厘米;3.14×(20÷2)?×3=942(立方厘米)
我爱展示
1.6.28立方分米
解析:由圆柱体的侧面积公式求出圆柱体的底面半径,最后根据圆柱体体积公式求出答案。列式:3.14×(12.56÷2÷3.14÷2)?×2=6.28(立方分米)
2.11304千克
解析:首先根据底面周长求出圆柱体的半径。
能装小麦的重量为:3.14×(9.42÷3.14÷2)?×2×800=11304(千克) 答:略。
3.602.88立方分米
解析:根据题意,把一个长方体,长8分米,宽8分米,高12分米,把它削成一个最大的圆柱,这个圆柱体的直径等于长方 体的长、宽,圆柱的高等于长方体的高,根据圆柱的体积公式:V=sh,把数据代入公式解答。
列式:3.14×(8÷2)?×12=602.88(立方分米) 答:略。
4.1004.8立方厘米
解析:由分析可知,这块铁件的体积是:3.14×8?×5=3.14×64×5 =1004.8(立方厘米) 答:略。
导学二
知识点讲解 1:圆柱体切割与表面积的联系例题
1.2;125.6
解析:把圆柱体转化成长方体来求体积,这是书本圆柱体积的推导方法,增加的表面积为长方体左右两边的长方形,长方 体和圆柱体的高一样,长方体的宽为圆柱体的底面半径,根据增加的表面积求出圆柱体的底面半径。
底面半径:40÷2÷10=2(cm); 圆柱体积:3.14×2?×10=125.6(cm?) 2.157立方厘米
解析:圆柱体的高截短,表面积减少部分展开图为一个长方形,其中长是底面周长,宽是2cm,求出底面周长,根据公式V=π(C÷2π)?h可求出减少的体积。
圆柱体的底面周长:62.8÷2=31.4(cm);
减少的体积:3.14×(31.4÷3.14÷2)?×2=157(cm?) 答:略。
我爱展示
1.10立方分米。
解析:把圆柱形木条截成三段小圆柱形木条,表面积增加的部分是4个相同的底面面积,根据增加的表面积可以求出原来 圆柱形木条的底面面积,根据公式V=Sh进行计算。计算前要先统一单位。
列式:1米=10分米;4÷4×10=10(立方分米)
答 : 略 。 2.120平方分米
解析:把圆柱体沿着底面直径劈开,增加的表面积是2个长方形,其中长方形的长是圆柱体底面的直径,宽圆柱体的高。 计算前要先统一单位。
列式:1米=10分米;3×2×10×2=120(平方分米) 答:略。
3.56.52立方厘米
解析:把圆柱体的高增高,表面积增加部分展开图为一个长方形,其中长是底面周长,宽是2cm,求出底面周长,根据公 式V=π(C÷2π)?h可求出圆柱体的增加体积。
圆柱体的底面周长:37.68÷2=18.84(cm);
增加的体积:3.14×(18.84÷3.14÷2)?×2=56.52(cm?) 答:略。
限时考场模拟
1.对
解析:圆柱体的侧面展开图是一个正方形,相当于底面周长等于圆柱体的高。2.12.56;18.84;6.28
解析:通过底面周长可以求出该圆柱体底面圆形的半径。3.8
解析: 围成的圆柱形纸筒侧面积为长方形的面积。列式:4×2=8(平方分米)
4.圆柱;157
解析:长方形绕轴旋转一周,得到的立体图形是圆柱,半径为原来长方形的长,高为原来长方形的宽。列式:3.14×5?×2=157(立方厘米)
5.75.36
解析:截成同样长的4段,相当于切3次。切1次增加2个横截面,切3次增加6个面。增加的面积:3.14×2×2×6=75.36(平方分米)
6.50.868平方米
解析:镶瓷砖的面积=一个底面面积+圆柱形侧面积。
列式:3.14×(6÷2)?+3.14×6×1.2=50.868(平方米)
答:略。
7.长:42cm;宽:28cm;高:12cm。
课后作业
1.C
2.B
3.A
4.D
5.A
解析:根据公式V=πr?h,题目中r=2dm,h=4dm,代入公式即可求出答案。6.302
解析:笔筒没有顶面,也就是铁皮面积=一个圆柱形底面面积+圆柱形侧面积。保留整数要使用进一法。 S铁=3.14×4×4+2×3.14×4×10=3.14×96=301.44(平方厘米)≈302(平方厘米)
7.62.8
解析:侧面展开图是正方形,说明该油桶的底面周长与高一样。h=C=2πr=2×3.14×10=62.8(厘米) 8.3;75.36
解析:截成四段小圆柱,相当于截3次,截1次增加2个底面,截3次增加6个底面。 S增=6×3.14×(12.56÷2÷3.14)?=75.36(平方分米)
9.1570
解析:圆柱体转化成长方体来求体积,这是书本圆柱体积的推导方法,增加的表面积为长方体左右两边的长方形,长方体 和圆柱体的高一样,长方体的宽为圆柱体的底面半径,根据增加的表面积求出圆柱体的底面半径。
r=200÷2÷20=5(厘米),V柱=3.14×5×5×20=1570(立方厘米) 10.62.8平方米
解析:前轮转动一周,压路的面积是圆柱形前轮的侧面积。列式:2×3.14×0.5×2×10=62.8(平方米)
答:略。11.37.68分米
解析:圆柱体的体积和长方体的体积一样,利用等体积转换即可求出长方体的高。列式:3.14×(8÷2)?×6÷(4×2)=37.68(分米)。
答:略。
12.1900平方厘米;7.536千克。
解析:底面半径:20÷2=10(厘米);
底面积是:3.14×10×10=314(平方厘米);
侧面积是:3.14×20×24=1507.2(平方厘米);
要用铁皮:314+1507.2=1821.2(平方厘米)≈1900(平方厘米); 水桶容积:3.14×10?×24=314×24=7536(毫升)=7.536(升); 水桶可盛水:7.536×1=7.536(千克)
答:略。
13.592.5平方厘米;785立方厘米。
解析:每块的表面积为圆柱表面积的一半加一个长方形面积。
每块的表面积是:[(10÷2)?×3.14×2+10×3.14×20]÷2+10×20=392.5+200=592.5(平方厘米);
每块的体积是:3.14×(10÷2)?×20÷2=785(立方厘米) 答:略。
14.50.24千克;12.56平方米;50240升
解析:圆柱形底面半径:12.56÷3.14÷2=2(米);
需要水泥:(12.56×4+3.14×2?)×0.8=50.24(千克); 占地面积是:3.14×2?=12.56(平方米);
水池可盛水:3.14×2?×4=50.24(立方米)=50240(升) 15.70.65立方厘米
解析:圆柱的底面周长是:18.84÷2=9.42(厘米); 圆柱的底面半径是:9.42÷3.14÷2=1.5(厘米);
原来圆柱的体积是: 3.14×1.5?×10=70.65(立方厘米) 16.1413米;2119.5平方米。
解析:公路长为:3.14×1×450=1413(米); 压过的路面是:1413×1.5=2119.5(平方米) 17.12盒
解析:3分米=30厘米;3.6分米=36厘米;2.4分米=24厘米; 底面直径:37.68÷3.14=12(厘米);
每箱最多可装奶粉:36÷12=3(盒);24÷12=2(盒);30÷152(盒);3×2×2=12(盒)
学生姓名
年级
学科
授课教师
日期
时段
核心内容
掌握圆柱的表面积和体积的计算
课型
一对一/一对N
教学目标
1、理解圆柱表面积意义,掌握体积公式的推导方法。
2、能够灵活运用公式计算圆柱的表面积与体积。
3、掌握圆柱体的切割类型题目。
重、难点
重点:教学目标1、2 难点:教学目标3
2532894114886
课首沟通
了解学生对圆柱体表面积以及体积的掌握情况。
知识导图
36830090319
课首小测
两个圆柱体的侧面积相等,它们的体积一定相等。( )
两个圆柱底面积和高分别相等,它们的体积也相等。( )
如果两个圆柱的体积相等,那么它们的底面积和高分别相等。( )
一个圆柱体和一个长方体高相等,底面周长相等,它们的体积也相等。( )
圆柱体底面积和高都扩大2倍,体积就扩大4倍。( )
[单选题] 圆柱体的底面半径和高都扩大2倍,它的体积扩大( )倍。
A.2 B.4 C.6 D.8
[单选题] 等底等高的圆柱体、正方体、长方体的体积相比较,( )。
A.正方体体积大 B.长方体体积大 C.圆柱体体积大 D.一样大
8. [单选题]
圆柱体的底面半径扩大3倍,高不变,体积扩大(
)。
A.3倍
B.9倍
C.6倍
9. [单选题] 求长方体、正方体、圆柱体的体积共同的公式是( )。
A.V=abh B.V= C.V=Sh 10. [单选题] 压路机的前轮转动一圈能压多少路面是指( )。
A.前轮的两个圆的面积 B.前轮的表面积 C.前轮的周长 D.前轮的侧面积
11. [单选题] 把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?
( )。
A.表面积和体积都没变 B.表面积和体积都发生了变化
C.表面积变了,体积没变 D.表面积没变,体积变了
2532894143560
导学一 : 圆柱表面积和体积求解的特殊类型
知识点讲解 1:求圆柱体表面积的特殊类型
侧面积:圆柱的侧面展开是一个长方形或正方形,长方形的长等于圆柱的底面周长(C=2πr=(d),宽等于圆柱的高。 S侧 =Ch =2πr h=πdh
侧面积公式的应用:
①已知C和h,求S侧; ②已知d和h,求S侧; ③已知r和h,求S侧。表面积: S表 = S侧+2S底=Ch+2πr?
表面积公式的应用:
①求一个底面积和侧面积(无盖的桶、茶杯、水池等);②只求侧面积(压路机、排水管、烟囱、通风管等)。
368300228907例 1. 如下图,高都是10厘米,底面半径分别是3厘米、6厘米的两个圆柱组成了一个几何体。求这个物体的表面积。
6131302237469例 2. 在一个棱长4厘米的正方体的六个面各中心挖去一个底面半径为1厘米,深1厘米的圆柱,求它的表面积。
例 3. 有一张长方形铁皮如图所示,剪下阴影部分制成圆柱体(单位:厘米),求这个圆柱体的表面积。(提示:圆桶盖的周长等于长方形铁皮的长)
我爱展示
圆柱的高都是1米,底面半径分别是1米、2米和3米。求这个物体的表面积。
36830093470
368300454904有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的直孔,如下图.圆孔的直径是4厘 米,孔深5厘米.如果将这个零件接触空气部分涂上防锈漆,一共需涂多少平方厘米?
377550200261把一张铁皮如图所示剪开,正好能制成一只铁皮汽油桶,求所制汽油桶的表面积。
知识点讲解 2:求圆柱体体积的特殊类型
体积: V柱=S底h=πr?h 圆柱体积公式的应用:
①已知S底和h,求V;②已知r和h,求V;③已知d和h,求V;④已知C和h,求V。
例 1. 一个圆柱体的体积是640立方厘米,底面积是80平方厘米,它的高是多少厘米?
例 2. 把一块长10厘米,宽1.57厘米,高10厘米的长方体橡皮泥,捏成直径是2厘米的圆橡皮泥条,橡皮泥条长多少厘米?
例 3. 把棱长是8厘米的正方体木块,削成一个最大的圆柱,圆柱体的体积是多少?
例 4. 一只钢管,长100厘米,外直径20厘米,内直径是16厘米,每立方厘米钢重8.2克,这只钢管重多少千克?
例 5. 有一个圆柱形水桶,底面直径2分米,盛水未满,放入一个铁球,当铁球完全沉入水中之后,水面升高3厘米,求铁球的体积?
我爱展示
一个圆柱体的侧面积是12.56平方分米,高2分米,它体积是( )。
一个圆柱形粮囤的底面周长是9.42米,高是2米,每立方米小麦重800千克,这个粮囤能装小麦多少千克?
一个长方体,长8分米,宽8分米,高12分米。把它削成一个最大的圆柱,这个圆柱的体积为多少立方分米?
一个圆柱形水槽,底面半径是8厘米,水槽中完全浸没着一块铁件,当铁件取出时,水面下降了5厘米。这块铁件的体 积是多少立方厘米?
导学二 : 圆柱体切割
知识点讲解 1:圆柱体切割与表面积的联系
① 圆柱的切割变化时,注意比较观察增加(减少)的面;
② 确定已知条件、未知条件,检查单位是否统一,正确选用公式计算。
例 1. 把高10厘米的圆柱体按下图切开,拼成近似的长方体,表面积就增加了40平方厘米,这个圆柱体的底面半径是
( )厘米,体积是( )立方厘米。
例 2. 一个圆柱体,如果把它的高截短2厘米,表面积就减少62.8平方厘米,那么它的体积就减少多少立方厘米?
我爱展示
368300403242将一根长1米圆柱形木条截成三段小圆柱形木条,表面积增加4平方分米,这根圆柱形木条原来的体积是多少立方分 米?
371805193901将一根长1米,底面半径为3分米的圆柱体木料,沿着底面直径劈开,表面积增加了多少平方分米?
一个圆柱体,如果把它的高增加2厘米,表面积就增加37.68平方厘米,那么这个圆柱体的体积增加了多少立方厘米?
2532894130072
限时考场模拟 : 15分钟
(2014年大联盟小升初真题)一个圆柱体的侧面展开图是一个正方形,此圆柱底面直径与高的比是1:π。( )
一个圆柱的底面周长是6.28分米,高2分米,它的侧面积是( )平方分米,表面积是( )平方分米,体积是( )立方分米。
用一张长4分米,宽2分米的长方形纸,围成一个圆柱形纸筒,它的侧面积是( )平方分米。
(2014年天河区小学毕业考试题)如图,将这个长方形绕轴旋转一周,得到的立体图形是( ),它的体积是( )cm?。
一根长4米,横截面半径为2分米的圆柱形木料截成同样长的4段,表面积比原来增加( )平方分米。
372871194799一个圆柱形水池,水池内壁和底面都要镶上瓷砖,水池底面直径6米,池深1.2米。镶瓷砖的面积是多少平方米?
368300412166某种饮料罐的形状为圆柱形,底面直径是7cm,高是12cm。将24罐这种饮料按如图所示的方式放入箱内,这个纸箱的 长、宽、高至少各是多少厘米?
课后作业
1. [单选题]
A.侧面积
一只铁皮水桶能装多少升水是求水桶的(
B.表面积
)。
C.容积
D.体积
[单选题] 做一只圆柱形的油桶,至少要用多少铁皮,是求油桶的( )。
A.侧面积 B.表面积 C.容积 D.体积
[单选题] 做一节圆柱形铁皮通风管要用多少铁皮,是求通风管的( )。
A.侧面积 B.表面积 C.容积 D.体积
[单选题] 求一段圆柱形钢条有多少立方米,是求钢条的( )。
A.侧面积 B.表面积 C.容积 D.体积
[单选题] 把一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米。
A.50.24 B.100.48 C.64
(2013年大联盟小升初真题)做一个圆柱形的笔筒,底面半径是4厘米,高是10厘米,做这个笔筒至少需要(
)平方厘米的铁皮。(保留整数)
一个圆柱形油桶,侧面展开是一个正方形,已知这个油桶的底面半径是10厘米,那么油桶的高是( )厘米。
(2011年天河区小学毕业考试题)一根圆柱形木料底面周长是12.56分米,高是6米。如果把它截成四段小圆柱,需要 截( )次,表面积增加( )平方分米。
把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体,表面积比原来增加了200平方厘米。已知 圆柱高20厘米,圆柱的体积是( )立方厘米。
(2010年天河区小学毕业考试题)一台压路机的前轮是圆柱形,轮宽2米,半径0.5米。前轮转动10周,压路的面积 是多少平方米?
(2010年大联盟小升初试题)把一块底面直径8分米、高6分米的圆柱体铜块熔铸成一个长方体,这个长方体长4分 米、宽2分米,它的高是多少分米?
一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米。做这个水桶要用铁皮多少平方厘米?(得数保留 整百平方厘米)这个水桶可以盛水多少千克?(每升水重1千克)
有一根圆柱形的木棒,直径是10厘米,高是20厘米,沿着直径锯成相等的两块,每块的表面积是多少?每块的体积 是多少?
一个圆柱形水池,从里面量底面周长是12.56米,深4米,如果在池底和池壁抹一层水泥,每平方米使用水泥0.8千 克,需要水泥多少千克?这个水池的占地面积是多少?这个水池可以盛水多少升?
有一个高是10厘米的圆柱,如果它的高减少2厘米,表面积就减少18.84平方厘米,原来圆柱的体积是多少立方厘 米?
压路机的前轮是圆柱,底面直径是1米,长是1.5米,从一条公路的一端压到另一端,共滚动了450周,这条公路有多 长?压过的路面有多少平方米?
一种圆柱形的奶粉盒底面周长是37.68厘米,高15厘米,如果装在长3分米、宽3.6分米、高2.4分米的长方体纸箱 内,每箱最多可以装多少盒奶粉?
2532894241365
1、课后先复习本节课的内容;
2、认真完成本堂课的课后作业;
3、本堂课中的错题誊写到错题本上,下节课会对错题进行练习。
2532894212031
课首小测
1.错
解析:因为把同一个长方形可以卷成体积不同的两个圆柱体,所以体积也相等是错误的表述。2.对
解析:根据公式V=Sh,可知它们的体积也相等。3.错
解析:圆柱的体积是V=Sh,S=π r?,所以V=π r?h,V相等,r和h的组合很多,并不一定是它们的底面积和高分别相等 ,所以是错误的。
4.错
解析:底面周长相等的情况下,圆的底面积最大,所以体积应该是圆柱体较大。5.对
解析:根据公式V=Sh,可知体积扩大4倍。6.D
解析:根据公式V=π r?h,可知体积应扩大8倍。7.D
解析:根据公式V=Sh,可知它们的体积也相等。8.B
解析:根据公式V=πr?h,可知体积应扩大9倍。9.C
解析:根据公式V=Sh,都可以分别求出这三个立方体的体积。10.D
解析: 表面积的实际应用,结合生活实际情况,与地面接触的是圆柱体的侧面积。11.C
解析:把圆柱体切拼成长方体,这是书本圆柱体体积的推导方法,表面积会变化,体积依然没有变。
导学一
知识点讲解 1:求圆柱体表面积的特殊类型例题
1.791.28平方厘米
解析:图中几何体是由2个圆柱体组成,分别求出两个圆柱体侧面展开图的面积,大圆柱体的两个底面面积,两部分面积 相加即可求出该物体的表面积。
列式:2×3.14×3×10+2×3.14×6×10+3.14×6?×2
=3.14×(60+120+72)
=791.28(平方厘米) 2.133.68平方厘米
解析:这个物体的表面积是棱长为4厘米的正方体的面积,加上6个底面半径为1厘米、高1厘米的的小圆柱体的侧面积,据 此解答即可。
列式:4×4×6+3.14×1×2×1×6=96+37.68=133.68(平方厘米)
3.131.88平方厘米
解析:观察图形可知,组成这个圆柱体的底面积周长为18.84厘米,利用公式C=πd求出圆柱体底面直径d,圆柱体高为10 减去直径d,圆柱体表面积=阴影长方形面积+两个圆面积。
圆柱的底面直径是:18.84÷3.14=6(厘米); 圆柱体的高是:10-6=4(厘米);
圆柱体表面积是:18.84×4+3.14×(6÷2)?×2=131.88(平方厘米)。答:略。
我爱展示
1.94.2平方米
解析:分别求出图中三个圆柱体的侧面展开图的面积,之后求出最大圆柱体的两个底面面积,两部分相加即可求出这个物 体的表面积。
列式:3.14×3?×2+3.14×(1×2+2×2+3×2)×1=94.2(平方米)
答 : 略 。 2.307.72平方厘米
解析:涂漆的面积是:3.14×(6÷2)?×2+3.14×6×10+3.14×4×5=307.72(平方厘米) 答:略。
3.31.4平方分米
解析:观察图形可知,组成的这个圆柱的高为两个圆的直径,底面周长为直径加上圆形周长。汽油桶底面直径:8.28÷(3.14+1)=2(分米)
汽油桶表面积:3.14×(2÷2)?×2+(8.28-2)×2×2=31.4(平方分米)
知识点讲解 2:求圆柱体体积的特殊类型例题
1.8厘米
解析:640÷80=8(厘米) 答:略。
2.50厘米
解析:长方体的体积:10×1.57×10=157(立方厘米); 橡皮泥条底面积: 3.14×(2÷2)?=3.14(平方厘米); 橡皮泥条长:157÷3.14=50(厘米)
3.401.92立方厘米
解析:要使圆柱体最大,正方体的棱长是圆柱体底面直径,根据体积公式即可求出答案。列式:3.14×(8÷2)?×8=401.92(立方厘米)
4.926.928千克
解析:钢管的体积=直径为20厘米的圆柱体体积-直径为16厘米的圆柱体体积。钢管的体积为:3.14×[(20÷2)?-(16÷2)?]×100=11304(立方厘米); 钢管重为:11304×8.2=92692.8(克);92692.8克=92.6928千克
答 : 略 。 5.942立方厘米
解析:铁球体积为水面升高后增加的体积。
列式:2分米=20厘米;3.14×(20÷2)?×3=942(立方厘米)
我爱展示
1.6.28立方分米
解析:由圆柱体的侧面积公式求出圆柱体的底面半径,最后根据圆柱体体积公式求出答案。列式:3.14×(12.56÷2÷3.14÷2)?×2=6.28(立方分米)
2.11304千克
解析:首先根据底面周长求出圆柱体的半径。
能装小麦的重量为:3.14×(9.42÷3.14÷2)?×2×800=11304(千克) 答:略。
3.602.88立方分米
解析:根据题意,把一个长方体,长8分米,宽8分米,高12分米,把它削成一个最大的圆柱,这个圆柱体的直径等于长方 体的长、宽,圆柱的高等于长方体的高,根据圆柱的体积公式:V=sh,把数据代入公式解答。
列式:3.14×(8÷2)?×12=602.88(立方分米) 答:略。
4.1004.8立方厘米
解析:由分析可知,这块铁件的体积是:3.14×8?×5=3.14×64×5 =1004.8(立方厘米) 答:略。
导学二
知识点讲解 1:圆柱体切割与表面积的联系例题
1.2;125.6
解析:把圆柱体转化成长方体来求体积,这是书本圆柱体积的推导方法,增加的表面积为长方体左右两边的长方形,长方 体和圆柱体的高一样,长方体的宽为圆柱体的底面半径,根据增加的表面积求出圆柱体的底面半径。
底面半径:40÷2÷10=2(cm); 圆柱体积:3.14×2?×10=125.6(cm?) 2.157立方厘米
解析:圆柱体的高截短,表面积减少部分展开图为一个长方形,其中长是底面周长,宽是2cm,求出底面周长,根据公式V=π(C÷2π)?h可求出减少的体积。
圆柱体的底面周长:62.8÷2=31.4(cm);
减少的体积:3.14×(31.4÷3.14÷2)?×2=157(cm?) 答:略。
我爱展示
1.10立方分米。
解析:把圆柱形木条截成三段小圆柱形木条,表面积增加的部分是4个相同的底面面积,根据增加的表面积可以求出原来 圆柱形木条的底面面积,根据公式V=Sh进行计算。计算前要先统一单位。
列式:1米=10分米;4÷4×10=10(立方分米)
答 : 略 。 2.120平方分米
解析:把圆柱体沿着底面直径劈开,增加的表面积是2个长方形,其中长方形的长是圆柱体底面的直径,宽圆柱体的高。 计算前要先统一单位。
列式:1米=10分米;3×2×10×2=120(平方分米) 答:略。
3.56.52立方厘米
解析:把圆柱体的高增高,表面积增加部分展开图为一个长方形,其中长是底面周长,宽是2cm,求出底面周长,根据公 式V=π(C÷2π)?h可求出圆柱体的增加体积。
圆柱体的底面周长:37.68÷2=18.84(cm);
增加的体积:3.14×(18.84÷3.14÷2)?×2=56.52(cm?) 答:略。
限时考场模拟
1.对
解析:圆柱体的侧面展开图是一个正方形,相当于底面周长等于圆柱体的高。2.12.56;18.84;6.28
解析:通过底面周长可以求出该圆柱体底面圆形的半径。3.8
解析: 围成的圆柱形纸筒侧面积为长方形的面积。列式:4×2=8(平方分米)
4.圆柱;157
解析:长方形绕轴旋转一周,得到的立体图形是圆柱,半径为原来长方形的长,高为原来长方形的宽。列式:3.14×5?×2=157(立方厘米)
5.75.36
解析:截成同样长的4段,相当于切3次。切1次增加2个横截面,切3次增加6个面。增加的面积:3.14×2×2×6=75.36(平方分米)
6.50.868平方米
解析:镶瓷砖的面积=一个底面面积+圆柱形侧面积。
列式:3.14×(6÷2)?+3.14×6×1.2=50.868(平方米)
答:略。
7.长:42cm;宽:28cm;高:12cm。
课后作业
1.C
2.B
3.A
4.D
5.A
解析:根据公式V=πr?h,题目中r=2dm,h=4dm,代入公式即可求出答案。6.302
解析:笔筒没有顶面,也就是铁皮面积=一个圆柱形底面面积+圆柱形侧面积。保留整数要使用进一法。 S铁=3.14×4×4+2×3.14×4×10=3.14×96=301.44(平方厘米)≈302(平方厘米)
7.62.8
解析:侧面展开图是正方形,说明该油桶的底面周长与高一样。h=C=2πr=2×3.14×10=62.8(厘米) 8.3;75.36
解析:截成四段小圆柱,相当于截3次,截1次增加2个底面,截3次增加6个底面。 S增=6×3.14×(12.56÷2÷3.14)?=75.36(平方分米)
9.1570
解析:圆柱体转化成长方体来求体积,这是书本圆柱体积的推导方法,增加的表面积为长方体左右两边的长方形,长方体 和圆柱体的高一样,长方体的宽为圆柱体的底面半径,根据增加的表面积求出圆柱体的底面半径。
r=200÷2÷20=5(厘米),V柱=3.14×5×5×20=1570(立方厘米) 10.62.8平方米
解析:前轮转动一周,压路的面积是圆柱形前轮的侧面积。列式:2×3.14×0.5×2×10=62.8(平方米)
答:略。11.37.68分米
解析:圆柱体的体积和长方体的体积一样,利用等体积转换即可求出长方体的高。列式:3.14×(8÷2)?×6÷(4×2)=37.68(分米)。
答:略。
12.1900平方厘米;7.536千克。
解析:底面半径:20÷2=10(厘米);
底面积是:3.14×10×10=314(平方厘米);
侧面积是:3.14×20×24=1507.2(平方厘米);
要用铁皮:314+1507.2=1821.2(平方厘米)≈1900(平方厘米); 水桶容积:3.14×10?×24=314×24=7536(毫升)=7.536(升); 水桶可盛水:7.536×1=7.536(千克)
答:略。
13.592.5平方厘米;785立方厘米。
解析:每块的表面积为圆柱表面积的一半加一个长方形面积。
每块的表面积是:[(10÷2)?×3.14×2+10×3.14×20]÷2+10×20=392.5+200=592.5(平方厘米);
每块的体积是:3.14×(10÷2)?×20÷2=785(立方厘米) 答:略。
14.50.24千克;12.56平方米;50240升
解析:圆柱形底面半径:12.56÷3.14÷2=2(米);
需要水泥:(12.56×4+3.14×2?)×0.8=50.24(千克); 占地面积是:3.14×2?=12.56(平方米);
水池可盛水:3.14×2?×4=50.24(立方米)=50240(升) 15.70.65立方厘米
解析:圆柱的底面周长是:18.84÷2=9.42(厘米); 圆柱的底面半径是:9.42÷3.14÷2=1.5(厘米);
原来圆柱的体积是: 3.14×1.5?×10=70.65(立方厘米) 16.1413米;2119.5平方米。
解析:公路长为:3.14×1×450=1413(米); 压过的路面是:1413×1.5=2119.5(平方米) 17.12盒
解析:3分米=30厘米;3.6分米=36厘米;2.4分米=24厘米; 底面直径:37.68÷3.14=12(厘米);
每箱最多可装奶粉:36÷12=3(盒);24÷12=2(盒);30÷152(盒);3×2×2=12(盒)
