人教版小学数学六年级下册讲义 圆柱与圆锥单元整理复习(含答案)
文档属性
| 名称 | 人教版小学数学六年级下册讲义 圆柱与圆锥单元整理复习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 15:00:16 | ||
图片预览




文档简介
圆柱与圆锥单元整理复习
学生姓名
年级
学科
授课教师
日期
时段
核心内容
圆柱与圆锥单元整理复习
课型
一对一/一对N
教学目标
1、掌握圆柱与圆锥的特征及各部分的名称,理解侧面展开图与各部分之间的关系;
2、掌握圆柱与圆锥侧面积、表面积和体积的计算方法,等底等高圆柱与圆锥体积的倍比关系;
3、培养动手操作能力,发展空间观念,提高解决综合题型的能力;
4、提升面试技巧与能力。
重、难点
重点:教学目标1、2 难点:教学目标3、4
2532894114879
课首沟通
了解学生对圆柱与圆锥的特征及各部分之间关系的掌握情况,
是否熟练掌握圆柱与圆锥相关公式的计算方法,能否理解等底等高圆柱与圆锥体积之间的倍比关系。
373220329749知识导图
课首小测
1. 圆柱有( 有的高都(
)个底面和(
)。
)个侧面,底面是(
)的两个圆;圆柱有(
)条高,所
2. 圆锥有(
高,有( )条高。
)个底面和(
)个侧面,侧面是一个(
);( )到(
)的距离叫做
3. 如何计算圆柱的表面积?如何计算圆柱和圆锥的体积?
2532894131349
导学一 : 圆柱与圆锥的认识
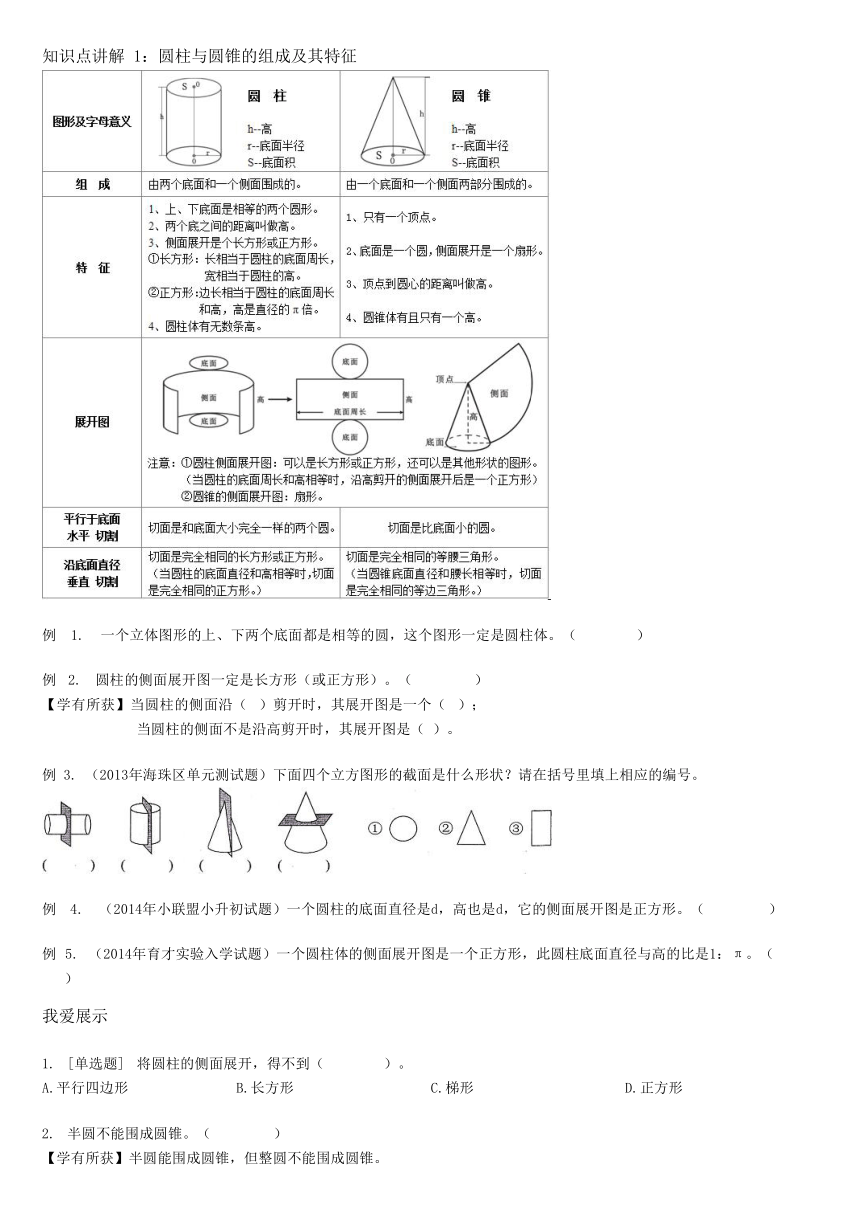
375398256663知识点讲解 1:圆柱与圆锥的组成及其特征
例 1. 一个立体图形的上、下两个底面都是相等的圆,这个图形一定是圆柱体。( ) 例 2. 圆柱的侧面展开图一定是长方形(或正方形)。( )
【学有所获】当圆柱的侧面沿( )剪开时,其展开图是一个( ); 当圆柱的侧面不是沿高剪开时,其展开图是( )。
375291198181例 3. (2013年海珠区单元测试题)下面四个立方图形的截面是什么形状?请在括号里填上相应的编号。
例 4. (2014年小联盟小升初试题)一个圆柱的底面直径是d,高也是d,它的侧面展开图是正方形。( ) 例 5. (2014年育才实验入学试题)一个圆柱体的侧面展开图是一个正方形,此圆柱底面直径与高的比是1:π。(
)
我爱展示
[单选题] 将圆柱的侧面展开,得不到( )。
A.平行四边形 B.长方形 C.梯形 D.正方形
半圆不能围成圆锥。( )
【学有所获】半圆能围成圆锥,但整圆不能围成圆锥。
把圆柱平行于底面水平切割,切面是和底面( )的两个( ), 把圆锥沿底面直径垂直切割,切面是完全相同的( )。
一个高6.28cm的圆柱侧面展开后是一个正方形,这个圆柱的底面周长是( )cm,底面半径是( ) cm。
如果圆柱的侧面展开后是正方形,那么圆柱的高是底面直径的3.14倍。 ( )
导学二 : 圆柱与圆锥的表面积与体积
375300300687知识点讲解 1:圆柱(与圆锥)的表面积
例 1. 要知道下列圆柱形物体用料的面积,需要求哪些面的总面积?
① 铁皮制成的糖果盒 ② 塑料制成的水管 ③ 玻璃制成的杯子
例 2. (2009年大联盟小升初试题)一个圆柱形水池,底面直径8米,高为直径的,若在水池内壁涂水泥,每平方米用水泥5千克,共需要( )千克。
例 3. 在一个棱长为2分米的正方体中,切下一个最大的圆柱,这个圆柱的侧面积是( )平方分米。
例 4. (2011年小联盟小升初试题)一辆压路机,前轮是一个大圆柱体,半径为1米,宽2米,工作时,前轮每分钟滚动10周,这台压路机的前轮每分钟压过的路面的面积是多少平方米?(圆周率约为3.14)
例 5. 一个圆柱体的侧面积是50.24cm?,高和底面半径相等,求圆柱体的表面积。
372890195863例 6. 圆柱的高都是1m,底面半径分别是1m、2m和3m。求这个物体的表面积。
371971194485例 7. (2013年海珠区单元测试题)右图是一个圆柱的表面展开图,这个圆柱的侧面积是多少?
我爱展示
圆柱形的油桶有( )个面,圆柱形的水池有( )个面,圆柱形的通风管有( )个面。
(2013年大联盟小升初试题)做一个圆柱形的笔筒,底面半径是 4 厘米,高是 10 厘米,做这个笔筒至少需要(
)平方厘米的铁皮。(保留整数)
一种压路机滚筒,直径是1.2米,长3米,每分钟转10周,每分钟压路机前进多少米?每分钟压路多少平方米?
[单选题] 把一个实心大圆柱切成3个同样大小的小圆柱,3个小圆柱的表面积之和比大圆柱的表面积多3.6dm?。大圆柱的底面积是( )。
A.1.2dm? B.0.9 dm? C.0.6 dm?
373263643484【学有所获】把一个立体图形一刀切开,表面积会增加,增加两个切面。 5. 把一张铁皮剪开,正好能制成一只铁皮汽油桶,求所制汽油桶的表面积。
知识点讲解 2:圆柱与圆锥的体积
容积: 立体图形容积的计算方法与计算体积的方法一样。
例 1. 一个圆柱形茶叶盒底面半径是10厘米,高是15厘米。它的体积是多少立方厘米?
375475196400例 2. (2013年海珠区单元测试题)计算右图物体体积。
例 3. 一个圆锥形沙堆,底面半径是3米,高是2米。如果每立方米沙重1.8吨。这堆沙重多少吨?
例 4. 一个长方形的长是6厘米,宽是2厘米。转一周所得到的圆柱体的体积是多少?
例 5. 一块直角三角形,两条直角边的长度分别是3厘米和2厘米,分别围绕两条直角边旋转一周,都可以得到一个圆锥体,较大圆锥体的体积是多少?较小的圆锥体体积是多少?
例 6. 把一个圆柱削成一个最大的圆锥,圆柱与圆锥的体积比是( )。若圆柱的体积是60立方分米,则削掉部分的体积是( )立方分米。
例 7. (2013年海珠区单元测试题)一个圆柱与一个圆锥体积相等,高也相等,圆柱的底面积是12cm?,那么圆锥的底面
积是4cm?。( )
【学有所获】利用公式,消除相等的数量,再找题目所求数量的等量关系。
例 8. (2012年大联盟小升初试题)一个圆锥与一个圆柱的底面积相等,已知圆锥与圆柱的体积比是1:9,圆锥的高是4.8厘米,则圆柱的高是( )厘米。
我爱展示
1. 一个圆柱体的底面半径是4厘米,高6厘米,它的体积是( )立方厘米; 一个圆柱体的底面直径是4厘米,高8厘米,它的体积是( )立方厘米;
一个圆柱体的底面周长是6.28分米,高2分米,它的体积是( )立方分米;
373171642587一个圆柱形米桶的底面直径是20米,高4.5米,这个米桶的容积是( )立方米。2. 求下面各形体的体积(单位:厘米)。
把一个棱长6厘米的正方体木料加工成一个最大的圆锥体,这个圆锥体的体积是( )立方厘米。
(2014年省实天河小升初试题)一个圆柱与一个圆锥体积相等,底面积也相等。已知圆柱的高是12cm,圆锥的高 是( )cm。
长4厘米,宽2厘米的长方形,沿边旋转形成两个不同的圆柱,这两个圆柱的体积差是多少?
一个圆锥形稻谷堆,底面周长是18.84米,高1米。如果每立方米稻谷重0.8吨,这堆稻谷重多少吨?
知识点讲解 3:圆柱与圆锥的表面积与体积的应用
问题(1)导入:把一块长10厘米,宽15.7厘米,高10厘米的长方体橡皮泥,捏成直径是2厘米的圆柱形橡皮泥条,橡皮 泥条长多少厘米?
解答:根据橡皮泥前后质量没变化,只是外形变了,由长方体捏成圆柱体,所以长方体的体积等于圆柱体的体积。 V柱=V长=10×15.7×10=1570(立方厘米), r=d÷2=2÷2=1(厘米)
橡皮泥的长即是圆柱体的高,h=V柱÷πr? =1570÷3.14÷1?=500(厘米) 答:橡皮泥条长500厘米。
★ 小结:等积变形,即形状变了,体积不变。先算出其中一个物体的体积,再算另一个物体的部分量。
问题(2)导入:把高10厘米的圆柱体按下图切开,拼成近似的长方体,表面积就增加了40平方厘米,这个圆柱体的底面 半径是多少厘米?体积是多少立方厘米?
解答:表面积增加在长方体左右两个面(长方形),长是圆柱的高,宽是圆柱的半径。r=40÷2÷10=2(厘米),V柱=πr? h=3.14×2?×10=125.6(立方厘米)
答:这个圆柱体的底面半径是2厘米,体积是125.6立方厘米。
★ 小结:立体图形切割变化时,注意比较观察增加(减少)的面,然后分析与立体图形各部分的联系。
370811505489问题(3)导入:有一个圆柱形水桶,底面直径2分米,盛水未满,放入一个铁球,当铁球完全沉入水中之后,水面升高3 厘米,求铁球的体积是多少?
解答:2分米=20厘米, r=d÷2=20÷2=10(厘米)
V铁球=V上升=πr? h升=3.14×10?×3=942(立方厘米) 答:铁球的体积是942立方厘米。
★ 小结:解决立体图形容积的实际问题(运用转化法和排水法): 上升(下降、溢出)水的体积=物体的体积
问题(4)导入:
① 一个圆柱体的底面半径扩大2倍,高不变,则底面直径扩大(
)倍,底面周长扩大(
)倍,
侧面积扩大( )倍,底面积扩大( )倍,体积扩大(
)倍;
② 两个圆柱体底面半径的比是1:2,高的比也是1:2,则底面直径的比是( ),底面周长的比是( ), 底面积的比是( ),体积的比是( )。
解答:
① 根据d=2 r,C=2 π r,S侧=2πrh可得:直径、周长、侧面积和半径的变化一致,半径扩大2倍,直径、底面周长和侧面积扩大2倍;根据S=πr?,V=πr? h可得:高相等,半径扩大2倍,底面积和体积扩大4倍。
② 根据d=2 r,C=2 π r可得:半径比=直径比=周长比;根据S=πr?可得:面积比=半径比的平方; 根据V=πr? h可得:体积比=半径比的立方;
所以底面直径的比是1:2,底面周长的比是1:2,底面积的比是1:4,体积的比是1:8。
★ 小结:两个相似的立体图形,当边的比都一样时,
周长比=边的比, 面积比=边的比的平方, 体积比=边的比的立方
例 1. (2013年海珠区单元测试题)一个圆锥形沙堆,底面积是37.5m?,高是2m,把这堆沙平铺在长8m,宽5m的长方形沙池中,可以铺多厚?
例 2. (2012年小联盟小升初试题)王芳买了一盒净含量为72立方厘米的牙膏,牙膏圆形出口直径为8毫米,她早晚各刷牙一次,每次挤出牙膏长约15毫米,这盒牙膏大约能供她使用多少天?(圆周率π取整数值3)
例 3. 将一根长1米,底面半径为4分米的圆柱体木料横锯成两段(不一定是平均分,锯成的两段后还是圆柱体),表面积增加了多少平方分米?
371805193732例 4. 将一根长1米,底面半径为3分米的圆柱体木料,沿着底面直径劈开,表面积增加了多少平方分米?
372419193756例 5. 有一个底面周长为25.12厘米的圆柱体,斜着截去一段后,剩下部分如图,求截去后剩下的体积?
例 6. (2008年广州小升初试题)一个圆柱体,如果把它的高截短2厘米,表面积就减少62.8平方厘米,那么它的体积就减
少( )立方厘米。
例 7. (2013年海珠区单元测试题)把一块石头完全浸没在底面半径为3.5dm的圆柱形容器的水里,水面上升了0.2dm(水没有溢出)。这块石头的体积是多少?
例 8. (2011年大联盟小升初试题)在一个底面半径为4厘米,高10厘米的圆柱形量杯内放入水,水面高8厘米,把一个小铁球放入水中,水满后还溢出15.7克,求小铁球的体积是多少?(1立方厘米的水重1克)
372716406645例 9. (2014年小联盟小升初试题)唐老鸭用一个圆锥形容器装满了2000克香油,米老鼠趁唐老鸭不在,在容器的中间咬了一个洞,然后开始偷油,一直偷到油面与小洞平齐为止。问:米老鼠共偷得香油多少克?(容器的厚度不计)
我爱展示
把一块长6cm,宽4cm,高5cm的铁块熔铸成一个高15cm的圆锥,这个圆锥的底面积是多少平方厘米?
374499241723把一根8m长的圆柱木材截成4段,表面积比原来增加75.36平方厘米,求原木材体积。
一个圆柱高8cm,如果它的高增加2cm,它的表面积将增加25.12cm?,求原来圆柱的体积。
371532405249一个底面直径是12cm的圆锥形木块,把它分成形状、大小完全相同的两个木块后,表面积比原来增加了120平方厘 米,这个圆锥形木块的体积是多少?
372958405824一个底面直径为20厘米的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6厘米,高为20厘米的圆椎形铅 锤,当铅锤从水中取出后,杯里的水将下降多少厘米?
2532894163486
限时考场模拟
1. ① 半圆不能围成扇形。( )
② 一个圆锥的体积是一个圆柱体积的。( )
375265618157③ 一个圆柱和一个圆锥等底等高,体积相差12.56cm?,圆柱的体积是18.84 cm?。( ) 2. 用一张长方形的纸片可以卷成一个圆柱体,下面的哪一个圆柱体是左边的长方形卷成的?
把2米长的圆柱形木条截成三段小圆柱形木条,表面积增加8平方分米,这根圆柱形木条原来的体积是多少立方分米?
一个圆柱的侧面沿高展开后是一个长12.56cm,宽6.28cm的长方形,求这个圆柱的底面半径。
一个圆柱形水槽,底面半径是8厘米,水槽中完全浸没着一块铁件,当铁件取出时,水面下降了5厘米。这块铁件的体 积是多少立方厘米?
课后作业
一个圆柱的底面半径是4dm,高是7dm,它的侧面积是( )dm?。
一个圆柱的侧面积是18.84m?,高是3m,它的底面积是( )m?。
一个圆柱与一个圆锥等底等高,圆锥的体积是19.2cm?,则圆柱的体积比圆锥的体积多( )cm?。
等底等高的圆柱和圆锥,已知它们的体积之差是24 dm?,则圆柱的体积是( )dm?。
一个圆柱和一个圆锥的底面积相等,体积也相等。圆柱的高是6dm,圆锥的高是( )dm。
① V=S h只能求圆柱的体积。( )
② 如果一个圆锥和一个圆柱的体积相等,底面积也相等,那么它们的高也一定相等。( )
③ 把一个底面积是4dm?,高是4dm的大圆柱截成4个相同的小圆柱,其表面积增加了24dm?。( )
④ 圆柱的侧面展开图可以是一个梯形。( )
⑤ 圆柱和圆锥都有无数条高。( )
[单选题] 求压路机的前轮转动一周能压多少路面就是求压路机前轮的( )。A.侧面积 B.表面积 C.体积
[单选题] 一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的( )倍。
B.4 C.6
[单选题] 一个圆锥的体积是3m?,底面积是3m?,它的高是( )m。
505825526214B.1 C.
[单选题] 在棱长是8cm的正方体上面的正中央向下挖一个底面直径是2cm,高是2cm的圆柱,则正方体的表面积增加
的部分是所挖圆柱的( )。
A.侧面积 B.侧面积+一个底面积 C.表面积
[单选题] 一个圆柱和一个圆锥的底面积相等,圆柱的高是圆锥的高的2倍,圆锥的体积是圆柱体积的(
)。
505825525674A. B. C.
368300401187计算下图的体积。(单位:cm)
一种圆柱形通风管的底面直径是8dm,长是60dm。制作12节这样的通风管至少需要多少平方米铁皮?
孔庙大成殿前檐有10根石雕圆柱,高约6m,直径约1m。如果每立方米石料重2.7吨,这些柱子约重多少吨?
一个圆锥形沙堆的底面周长是12.56m,高是1.8m。用这堆沙子在8m宽的公路上铺3cm厚的路面,能铺多少米?
373709406858一根长2m,横截面半径是20cm的木头浮在水面上,何小泉发现它正好是一半露出水面(如图),你知道这根木头露 出水面的面积是多少吗?
2532894157139
1、完成本堂课的课后作业;
2、把题目的关键字圈出,想清楚问题问的是什么,再开始做题;
3、本堂课中的错题誊写到错题本上,下节课会对错题进行练习。
课首小测
1.2;1;完全相等;无数;相等。
2.1;1;扇形;顶点;底面圆心;1。
3.圆柱的表面积:S表=S侧+2 S底=Ch+2πr?;圆柱的体积:V柱=S底h=πr? h,圆锥的体积:V锥=S底h= πr? h。
导学一
知识点讲解 1:圆柱与圆锥的组成及其特征例题
错
错
解析:圆柱的侧面只有沿着高剪开时,展开图才是一个长方形(或正方形)。3.①; ③; ②; ①。
4.错
解析:圆柱侧面展开图的一边是高(d),一边是底面周长(πd),d≠πd,所以侧面展开图不是正方形。 5.对
解析:圆柱的侧面展开图是一个正方形,高=底面周长=πd,底面直径:高=d:πd=1:π。
我爱展示
1.C
解析:沿着圆柱的高展开,可得到正方形或长方形,沿着斜边展开可得到平行四边形,但得不到梯形。2.错
解析:圆锥的侧面展开图是扇形,而半圆也是扇形,因此半圆能围成圆锥。3.大小完全一样;圆;等腰三角形。
4.6.28;1。
解析:圆柱的侧面展开图是一个正方形,底面周长=高=6.28cm;底面半径=C÷2π=6.28÷2÷3.14=1(cm)。 5.错
解析:圆柱的侧面展开图是一个正方形,高=底面周长=πd,高÷底面直径=πd÷d=π。
导学二
知识点讲解 1:圆柱(与圆锥)的表面积例题
1.① 求一个侧面积和两个底面积;② 求一个侧面积;③ 求一个侧面积和一个底面积。
2.1004.8
解析:h= d= ×8=6(米), r=d= ×8=4(米), S侧=πdh=3.14×8×6=150.72(平方米), S底=πr?=3.14×4?=50.24(平方米), (150.72+50.24)×5=1004.8(千克)
3.56平方米
解析:圆柱的高和直径就是正方体的棱长,d=h=2分米 S侧=πdh=3.14×2×2=12.56(平方分米)
4.6平方米
解析:每分钟压路多少平方米,就是求每分钟压了多少个侧面积。 S侧=Ch=2πrh=2×3.14×1×2×10=125.6(平方米)
答:这台压路机的前轮每分钟压过的路面的面积是125.6平方米。5.100.48cm?
解析:S侧=2(r h=2×3.14×r?=50.24,r?=50.24÷2÷3.14=8(cm?), S表= S侧+2 S底=50.24+2×3.14×8=50.24+50.24=100.48(cm?)
答:圆柱体的表面积是100.48cm?。6.94.2m?
解析:S侧1+S侧2+S侧3+2 S底=2×3.14×(1+2+3)+2×3.14×3?=37.68+56.52=94.2(m?) 答:这个物体的表面积是94.2m?。
7.48dm?
解析:长方形的长由圆的直径和底面周长组成, d+πd=16.56,d=16.56÷(1+π)=16.56÷4.14=4(dm)
高由两个相等的圆的直径组成,
S侧=Ch=πd×2d=3.14×4×2×4=100.48(dm?) 答:这个圆柱的侧面积是100.48dm?。
我爱展示
1.3;2;1。
2.301
解析:笔筒的表面积由一个侧面和一个底面组成,
S表=S侧+S底=2πrh+πr?=2×3.14×4×10+3.14×4?=251.2+50.24=301.44≈301(平方厘米) 3.37.68米;113.04平方米。
解析:每分钟前进多少米,就是求每分钟转了多少个周长。3.14×1.2×10=37.68(米)
每分钟压路多少平方米,就是求每分钟压了多少个侧面积。37.68×3=113.04(平方米) 答:每分钟压路机前进37.68米,每分钟压路113.04平方米。
4.B
解析:切成3个小圆柱,就是切了2刀,增加了(3-1)×2=4(面),S底=3.6÷4=0.9(dm?) 5.31.4dm?
解析:长方形的长由圆的直径和底面周长组成,d+πd=8.28,d=8.28÷(1+π)=8.28÷4.14=2(dm) 高由两个相等的圆的直径组成,h=2d=2×2=4(dm),r=d÷2=2÷2=1(dm)
S表=S侧+2 S底=πdh+2πr?=3.14×2×4+2×3.14×1?=25.12+6.28=31.4(dm?) 答:所制汽油桶的表面积是31.4dm?。
知识点讲解 2:圆柱与圆锥的体积例题
1.4710立方厘米
解析:V柱=S底h=πr? h=3.14×10?×15=4710(立方厘米) 答:它的体积是4710立方厘米。2.50.24立方米
解析:r=d÷2=4÷2=2(米)
V=V锥+V柱= S底h+S底h= S底h= ×3.14×2?×3=50.24(立方米) 3.33.912吨
解析:V锥= S底h= ×3.14×3?×2=18.84(立方米),18.84×1.8=33.912(吨)答:这堆沙重33.912吨。4.226.08立方厘米和75.36立方厘米
解析:以长为半径,宽为高:V柱1=3.14×6?×2=226.08(立方厘米) 以宽为半径,长为高:V柱2=3.14×2?×6=75.36(立方厘米)
答:转一周所得到的圆柱体的体积是226.08立方厘米和75.36立方厘米。5.18.84立方厘米;12.56立方厘米。
解析:V1=3.14×3?×2÷3=18.84(立方厘米); V2=3.14×2?×3÷3=12.56(立方厘米)
答:较大圆锥体的体积是18.84立方厘米,较小的圆锥体体积是12.56立方厘米。6.3:1;40。
18576152333372292384233337解析:削成的圆锥与圆柱等底等高,根据公式V柱=S底h,V锥= S底h,V柱:V锥=3:1;
削掉部分的体积: V柱= ×60=40(立方分米)。
7.错
1709609284048解析:已知V柱:V锥=1:1,h柱:h锥=1:1;根据公式V柱=S底h,V锥= S底h,得:
圆柱的S底×h= 圆锥的S底×h → 3圆柱的S底=圆锥的S底→ 圆锥的S底=3×12=36(cm?)。
8.14.4
解析:已知V柱:V锥=1:9,圆柱与圆锥的底面积相等;根据公式V柱=S底h,V锥= S底h,得:
V柱=9 V锥→ S底×h柱=9××S底×h锥 → h柱=3 h锥 → h柱=3×4.8=14.4(厘米)。
我爱展示
1.301.44;100.48;6.28;1413。
解析:V1=3.14×4?×6=301.44(立方厘米);V2=3.14×( )?×8=100.48(立方厘米); V3=3.14×( )?×2=6.28(立方分米);V4=3.14×( )?×4.5=1413(立方米)。2.10.99cm?
解析:r=d÷2=2÷2=1(cm),V=V柱-V锥=3.14×1?×4- ×3.14×1?×1.5=12.56-1.57=10.99(cm?)。3.56.52
解析:圆锥的底面直径和高等于正方体的棱长,V锥= S底h= ×3.14×( )?×6=56.52(立方厘米) 4.36
解析:圆柱和圆锥等体等底的情况下,根据公式V柱=S底h,V锥= S底h,得:
S底×h柱= S底×h锥 → h柱= h锥 → h锥=3 h柱=3×12=36(cm)。5.50.24立方厘米
解析:V1=3.14×4?×2=100.48(立方厘米), V2=3.14×2?×4=50.24(立方厘米) V1-V2=100.48-50.24(立方厘米)
6.7.536吨
解析:r=18.84÷2÷3.14=3(米), ×3.14×3?×1×0.8=7.536(吨) 答:这堆稻谷重7.536吨。
知识点讲解 3:圆柱与圆锥的表面积与体积的应用例题
1.0.625米
解析:V锥= ×37.5×2=25(立方米), h=25÷8÷5=0.625(米) 答:可以铺0.625米厚。
2.50天
解析:8毫米=0.8厘米,15毫米=1.5厘米,r=d÷2=0.8÷2=0.4(厘米)
V柱=3×0.4×0.4×1.5=0.72(立方厘米),72÷2÷0.72=50(天)答:这盒牙膏大约能供她使用50天。3.100.48平方分米
解析:增加的是两个圆形的底面积,2 S底=2×3.14×4?=100.48(平方分米) 答:表面积增加了100.48平方分米。
4.120平方分米
解析:增加的是两个长方形的面积,长方形的长是圆柱的高,长方形的宽是圆柱的底面直径
1米=10分米,d=2r=2×3=6(分米),S长=2×10×6=120(平方分米) 答:表面积增加了120平方分米。
5.251.2立方厘米
372307241795解析:如下图所示,用两个原来的立体图形拼成一个圆柱体,圆柱体的底面积不变,h=4+6=10(厘米)
r=25.12÷2÷3.14=4(厘米),V= V柱= ×3.14×4×4×10=251.2(立方厘米) 答:截去后剩下的体积是251.2立方厘米。
6.157
373094455172解析:画图观察,如果高截短了2厘米,两个底面积没有变化,虚线表示表面积减少的部分是一个长方形, 长方形的长是底面周长,宽是减少的2厘米。
根据S长=长×宽,可得:C=62.8÷2=31.4(厘米), r=31.4÷2÷3.14=5(厘米) V减=πr? h减=3.14×5?×2=157(立方厘米)
7.7.693立方分米
解析:V石=V升=πr? h升=3.14×3.5×3.5×0.2=7.693(立方分米) 答:这块石头的体积是7.693立方分米。
8.116.18立方厘米
解析:15.7÷1=15.7(立方厘米),V球=3.14×4×4×(10-8)+15.7=116.18(立方厘米) 答:小铁球的体积是116.18立方厘米。
9.1750克
解析:剩下的油和原来的油的体积相似,现在油的高度和原来油的高度比是1:2,那么它们的体积比是1:8, 即剩下的油的体积是原来的油的体积的 。米老鼠偷走了1- = ,2000× =1750(克)
答:米老鼠共偷得香油1750克。
我爱展示
1.24平方厘米
解析:V锥=V长=abh=6×4×5=120(立方厘米),S底=3 V锥÷h=3×120÷15=24(平方厘米) 答:这个圆锥的底面积是24平方厘米。
2.100.48立方厘米
解析:截成4段,就是切了3刀,(4-1)×2=6(面),S底=75.36÷6=12.56(平方厘米) V柱=S底h=12.56×8=100.48(立方厘米)
答:原木材体积是100.48立方厘米。3.100.48立方厘米
解析:增加的面积展开来是一个长方形,长方形的长是底面周长,宽是增加的2厘米。
根据S长=长×宽,可得:C=25.12÷2=12.56(厘米), r=12.56÷2÷3.14=2(厘米)
V柱=πr? h=3.14×2?×8=100.48(立方厘米) 答:原来圆柱的体积是100.48立方厘米。4.376.8立方厘米
解析:表面积增加的部分是两个以底面直径为底边,以圆锥的高为高的等腰三角形, S△=120÷2=60(平方厘米),h=2×60÷12=10(厘米),r=d÷2=12÷2=6(厘米) V锥= ×3.14×6×6×10=376.8(立方厘米)
答:这个圆锥形木块的体积是376.8立方厘米。
5.0.6厘米
解析:玻璃杯是是圆柱形的,铅锤取出后水面下降部分实际是一个小圆柱,这个圆柱的底面与玻璃杯的底面一样,是一个 直径为20厘米的圆,它的体积正好等于圆锥形铅锤的体积,小圆柱的高就是水面下降的高度。
V锥= ×3.14×( )?×20=188.4(立方厘米),S底=3.14×( )?=314(平方厘米)
h降=188.4÷314=0.6(厘米) 答:杯里的水将下降0.6厘米。
限时考场模拟
1.(1)×;(2)×;(3)√
2.①和③
解析:分析:如果用长方形长12.56cm作圆柱底面周长,则底面直径是12.56÷3.14=4(cm),高是3.14cm; 如果用长方形宽3.14cm作圆柱底面周长,则底面直径是3.14÷3.14=1(cm),高是12.56cm。
3.40立方分米
解析:h=2米=20分米,截成三段,增加了(3-1)×2=4(面),S底=8÷4=2(平方分米);
V柱=S底h=2×20=40(立方分米)。 答:这根圆柱形木条原来的体积是40立方分米。4.2cm或1cm
解析:如果以12.56cm 作为底面周长,r1=12.56÷2÷3.14=2(cm) 如果以6.28cm作为底面周长,r2=6.28÷2÷3.14=1(cm)
答:这个圆柱的底面半径是2cm或1cm。5.1004.8立方厘米
解析:V铁=S底h降=3.14×8×8×5=1004.8(立方厘米)答:这块铁件的体积是1004.8立方厘米。
课后作业
1.175.84
解析:S侧=2×3.14×4×7=175.84(dm?) 2.3.14
解析:r=18.84÷3÷2÷3.14=1(m), S底=3.14×1×1=3.14(m?) 3.38.4
解析:等底等高的圆柱与圆锥的体积比是3:1,V柱=3 V锥=3×19.2=57.6(cm?) 57.6-19.2=38.4(cm?)
4.36
解析:等底等高的圆柱与圆锥的体积比是3:1,V柱=24÷(3-1)×3=36(dm?) 5.18
解析:根据已知条件得:V柱=V锥,S底h柱= S底h锥 → h锥=3 h柱=3×6=18(dm)
6.(1)×;(2)×;(3)√;(4)×;(5)×
7.A
8.B
9.A
解析:h=3 V锥÷S底=3×3÷3=3(m) 10.A
11.C
解析:V锥= Sh, V柱=S×2h=2Sh, V锥÷V柱= Sh÷2Sh= 。12.1256cm?
解析:r=6÷2=3(cm),R=10÷2=5(cm),V=S环h=3.14×(5?-3?)×25=1256(cm?) 13.180.864平方米
解析:8分米=0.8米,60分米=6米,S侧×12=πdh=3.14×0.8×6×12=180.864(平方米) 答:制作12节这样的通风管至少需要180.864平方米铁皮。
14.127.17吨
解析:r=1÷2=0.5(米),V柱=3.14×0.5×0.5×6=4.71(立方米),4.71×10×2.7=127.17(吨) 答:这些柱子约重127.17吨。
15.31.4米
解析:r=12.56÷2÷3.14=2(米), V锥=×3.14×2×2×1.8=7.536(立方米) 3厘米=0.03米, 7.536÷8÷0.03=31.4(米)
答:能铺31.4米。16.138.16平方米
解析:2米=20分米,20厘米=2分米,S表=S侧+2 S底=2×3.14×2×20+2×3.14×2×2=276.32(平方米) 276.32÷2=138.16(平方米)
368300187563答:这根木头露出水面的面积是138.16平方米。
学生姓名
年级
学科
授课教师
日期
时段
核心内容
圆柱与圆锥单元整理复习
课型
一对一/一对N
教学目标
1、掌握圆柱与圆锥的特征及各部分的名称,理解侧面展开图与各部分之间的关系;
2、掌握圆柱与圆锥侧面积、表面积和体积的计算方法,等底等高圆柱与圆锥体积的倍比关系;
3、培养动手操作能力,发展空间观念,提高解决综合题型的能力;
4、提升面试技巧与能力。
重、难点
重点:教学目标1、2 难点:教学目标3、4
2532894114879
课首沟通
了解学生对圆柱与圆锥的特征及各部分之间关系的掌握情况,
是否熟练掌握圆柱与圆锥相关公式的计算方法,能否理解等底等高圆柱与圆锥体积之间的倍比关系。
373220329749知识导图
课首小测
1. 圆柱有( 有的高都(
)个底面和(
)。
)个侧面,底面是(
)的两个圆;圆柱有(
)条高,所
2. 圆锥有(
高,有( )条高。
)个底面和(
)个侧面,侧面是一个(
);( )到(
)的距离叫做
3. 如何计算圆柱的表面积?如何计算圆柱和圆锥的体积?
2532894131349
导学一 : 圆柱与圆锥的认识
375398256663知识点讲解 1:圆柱与圆锥的组成及其特征
例 1. 一个立体图形的上、下两个底面都是相等的圆,这个图形一定是圆柱体。( ) 例 2. 圆柱的侧面展开图一定是长方形(或正方形)。( )
【学有所获】当圆柱的侧面沿( )剪开时,其展开图是一个( ); 当圆柱的侧面不是沿高剪开时,其展开图是( )。
375291198181例 3. (2013年海珠区单元测试题)下面四个立方图形的截面是什么形状?请在括号里填上相应的编号。
例 4. (2014年小联盟小升初试题)一个圆柱的底面直径是d,高也是d,它的侧面展开图是正方形。( ) 例 5. (2014年育才实验入学试题)一个圆柱体的侧面展开图是一个正方形,此圆柱底面直径与高的比是1:π。(
)
我爱展示
[单选题] 将圆柱的侧面展开,得不到( )。
A.平行四边形 B.长方形 C.梯形 D.正方形
半圆不能围成圆锥。( )
【学有所获】半圆能围成圆锥,但整圆不能围成圆锥。
把圆柱平行于底面水平切割,切面是和底面( )的两个( ), 把圆锥沿底面直径垂直切割,切面是完全相同的( )。
一个高6.28cm的圆柱侧面展开后是一个正方形,这个圆柱的底面周长是( )cm,底面半径是( ) cm。
如果圆柱的侧面展开后是正方形,那么圆柱的高是底面直径的3.14倍。 ( )
导学二 : 圆柱与圆锥的表面积与体积
375300300687知识点讲解 1:圆柱(与圆锥)的表面积
例 1. 要知道下列圆柱形物体用料的面积,需要求哪些面的总面积?
① 铁皮制成的糖果盒 ② 塑料制成的水管 ③ 玻璃制成的杯子
例 2. (2009年大联盟小升初试题)一个圆柱形水池,底面直径8米,高为直径的,若在水池内壁涂水泥,每平方米用水泥5千克,共需要( )千克。
例 3. 在一个棱长为2分米的正方体中,切下一个最大的圆柱,这个圆柱的侧面积是( )平方分米。
例 4. (2011年小联盟小升初试题)一辆压路机,前轮是一个大圆柱体,半径为1米,宽2米,工作时,前轮每分钟滚动10周,这台压路机的前轮每分钟压过的路面的面积是多少平方米?(圆周率约为3.14)
例 5. 一个圆柱体的侧面积是50.24cm?,高和底面半径相等,求圆柱体的表面积。
372890195863例 6. 圆柱的高都是1m,底面半径分别是1m、2m和3m。求这个物体的表面积。
371971194485例 7. (2013年海珠区单元测试题)右图是一个圆柱的表面展开图,这个圆柱的侧面积是多少?
我爱展示
圆柱形的油桶有( )个面,圆柱形的水池有( )个面,圆柱形的通风管有( )个面。
(2013年大联盟小升初试题)做一个圆柱形的笔筒,底面半径是 4 厘米,高是 10 厘米,做这个笔筒至少需要(
)平方厘米的铁皮。(保留整数)
一种压路机滚筒,直径是1.2米,长3米,每分钟转10周,每分钟压路机前进多少米?每分钟压路多少平方米?
[单选题] 把一个实心大圆柱切成3个同样大小的小圆柱,3个小圆柱的表面积之和比大圆柱的表面积多3.6dm?。大圆柱的底面积是( )。
A.1.2dm? B.0.9 dm? C.0.6 dm?
373263643484【学有所获】把一个立体图形一刀切开,表面积会增加,增加两个切面。 5. 把一张铁皮剪开,正好能制成一只铁皮汽油桶,求所制汽油桶的表面积。
知识点讲解 2:圆柱与圆锥的体积
容积: 立体图形容积的计算方法与计算体积的方法一样。
例 1. 一个圆柱形茶叶盒底面半径是10厘米,高是15厘米。它的体积是多少立方厘米?
375475196400例 2. (2013年海珠区单元测试题)计算右图物体体积。
例 3. 一个圆锥形沙堆,底面半径是3米,高是2米。如果每立方米沙重1.8吨。这堆沙重多少吨?
例 4. 一个长方形的长是6厘米,宽是2厘米。转一周所得到的圆柱体的体积是多少?
例 5. 一块直角三角形,两条直角边的长度分别是3厘米和2厘米,分别围绕两条直角边旋转一周,都可以得到一个圆锥体,较大圆锥体的体积是多少?较小的圆锥体体积是多少?
例 6. 把一个圆柱削成一个最大的圆锥,圆柱与圆锥的体积比是( )。若圆柱的体积是60立方分米,则削掉部分的体积是( )立方分米。
例 7. (2013年海珠区单元测试题)一个圆柱与一个圆锥体积相等,高也相等,圆柱的底面积是12cm?,那么圆锥的底面
积是4cm?。( )
【学有所获】利用公式,消除相等的数量,再找题目所求数量的等量关系。
例 8. (2012年大联盟小升初试题)一个圆锥与一个圆柱的底面积相等,已知圆锥与圆柱的体积比是1:9,圆锥的高是4.8厘米,则圆柱的高是( )厘米。
我爱展示
1. 一个圆柱体的底面半径是4厘米,高6厘米,它的体积是( )立方厘米; 一个圆柱体的底面直径是4厘米,高8厘米,它的体积是( )立方厘米;
一个圆柱体的底面周长是6.28分米,高2分米,它的体积是( )立方分米;
373171642587一个圆柱形米桶的底面直径是20米,高4.5米,这个米桶的容积是( )立方米。2. 求下面各形体的体积(单位:厘米)。
把一个棱长6厘米的正方体木料加工成一个最大的圆锥体,这个圆锥体的体积是( )立方厘米。
(2014年省实天河小升初试题)一个圆柱与一个圆锥体积相等,底面积也相等。已知圆柱的高是12cm,圆锥的高 是( )cm。
长4厘米,宽2厘米的长方形,沿边旋转形成两个不同的圆柱,这两个圆柱的体积差是多少?
一个圆锥形稻谷堆,底面周长是18.84米,高1米。如果每立方米稻谷重0.8吨,这堆稻谷重多少吨?
知识点讲解 3:圆柱与圆锥的表面积与体积的应用
问题(1)导入:把一块长10厘米,宽15.7厘米,高10厘米的长方体橡皮泥,捏成直径是2厘米的圆柱形橡皮泥条,橡皮 泥条长多少厘米?
解答:根据橡皮泥前后质量没变化,只是外形变了,由长方体捏成圆柱体,所以长方体的体积等于圆柱体的体积。 V柱=V长=10×15.7×10=1570(立方厘米), r=d÷2=2÷2=1(厘米)
橡皮泥的长即是圆柱体的高,h=V柱÷πr? =1570÷3.14÷1?=500(厘米) 答:橡皮泥条长500厘米。
★ 小结:等积变形,即形状变了,体积不变。先算出其中一个物体的体积,再算另一个物体的部分量。
问题(2)导入:把高10厘米的圆柱体按下图切开,拼成近似的长方体,表面积就增加了40平方厘米,这个圆柱体的底面 半径是多少厘米?体积是多少立方厘米?
解答:表面积增加在长方体左右两个面(长方形),长是圆柱的高,宽是圆柱的半径。r=40÷2÷10=2(厘米),V柱=πr? h=3.14×2?×10=125.6(立方厘米)
答:这个圆柱体的底面半径是2厘米,体积是125.6立方厘米。
★ 小结:立体图形切割变化时,注意比较观察增加(减少)的面,然后分析与立体图形各部分的联系。
370811505489问题(3)导入:有一个圆柱形水桶,底面直径2分米,盛水未满,放入一个铁球,当铁球完全沉入水中之后,水面升高3 厘米,求铁球的体积是多少?
解答:2分米=20厘米, r=d÷2=20÷2=10(厘米)
V铁球=V上升=πr? h升=3.14×10?×3=942(立方厘米) 答:铁球的体积是942立方厘米。
★ 小结:解决立体图形容积的实际问题(运用转化法和排水法): 上升(下降、溢出)水的体积=物体的体积
问题(4)导入:
① 一个圆柱体的底面半径扩大2倍,高不变,则底面直径扩大(
)倍,底面周长扩大(
)倍,
侧面积扩大( )倍,底面积扩大( )倍,体积扩大(
)倍;
② 两个圆柱体底面半径的比是1:2,高的比也是1:2,则底面直径的比是( ),底面周长的比是( ), 底面积的比是( ),体积的比是( )。
解答:
① 根据d=2 r,C=2 π r,S侧=2πrh可得:直径、周长、侧面积和半径的变化一致,半径扩大2倍,直径、底面周长和侧面积扩大2倍;根据S=πr?,V=πr? h可得:高相等,半径扩大2倍,底面积和体积扩大4倍。
② 根据d=2 r,C=2 π r可得:半径比=直径比=周长比;根据S=πr?可得:面积比=半径比的平方; 根据V=πr? h可得:体积比=半径比的立方;
所以底面直径的比是1:2,底面周长的比是1:2,底面积的比是1:4,体积的比是1:8。
★ 小结:两个相似的立体图形,当边的比都一样时,
周长比=边的比, 面积比=边的比的平方, 体积比=边的比的立方
例 1. (2013年海珠区单元测试题)一个圆锥形沙堆,底面积是37.5m?,高是2m,把这堆沙平铺在长8m,宽5m的长方形沙池中,可以铺多厚?
例 2. (2012年小联盟小升初试题)王芳买了一盒净含量为72立方厘米的牙膏,牙膏圆形出口直径为8毫米,她早晚各刷牙一次,每次挤出牙膏长约15毫米,这盒牙膏大约能供她使用多少天?(圆周率π取整数值3)
例 3. 将一根长1米,底面半径为4分米的圆柱体木料横锯成两段(不一定是平均分,锯成的两段后还是圆柱体),表面积增加了多少平方分米?
371805193732例 4. 将一根长1米,底面半径为3分米的圆柱体木料,沿着底面直径劈开,表面积增加了多少平方分米?
372419193756例 5. 有一个底面周长为25.12厘米的圆柱体,斜着截去一段后,剩下部分如图,求截去后剩下的体积?
例 6. (2008年广州小升初试题)一个圆柱体,如果把它的高截短2厘米,表面积就减少62.8平方厘米,那么它的体积就减
少( )立方厘米。
例 7. (2013年海珠区单元测试题)把一块石头完全浸没在底面半径为3.5dm的圆柱形容器的水里,水面上升了0.2dm(水没有溢出)。这块石头的体积是多少?
例 8. (2011年大联盟小升初试题)在一个底面半径为4厘米,高10厘米的圆柱形量杯内放入水,水面高8厘米,把一个小铁球放入水中,水满后还溢出15.7克,求小铁球的体积是多少?(1立方厘米的水重1克)
372716406645例 9. (2014年小联盟小升初试题)唐老鸭用一个圆锥形容器装满了2000克香油,米老鼠趁唐老鸭不在,在容器的中间咬了一个洞,然后开始偷油,一直偷到油面与小洞平齐为止。问:米老鼠共偷得香油多少克?(容器的厚度不计)
我爱展示
把一块长6cm,宽4cm,高5cm的铁块熔铸成一个高15cm的圆锥,这个圆锥的底面积是多少平方厘米?
374499241723把一根8m长的圆柱木材截成4段,表面积比原来增加75.36平方厘米,求原木材体积。
一个圆柱高8cm,如果它的高增加2cm,它的表面积将增加25.12cm?,求原来圆柱的体积。
371532405249一个底面直径是12cm的圆锥形木块,把它分成形状、大小完全相同的两个木块后,表面积比原来增加了120平方厘 米,这个圆锥形木块的体积是多少?
372958405824一个底面直径为20厘米的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6厘米,高为20厘米的圆椎形铅 锤,当铅锤从水中取出后,杯里的水将下降多少厘米?
2532894163486
限时考场模拟
1. ① 半圆不能围成扇形。( )
② 一个圆锥的体积是一个圆柱体积的。( )
375265618157③ 一个圆柱和一个圆锥等底等高,体积相差12.56cm?,圆柱的体积是18.84 cm?。( ) 2. 用一张长方形的纸片可以卷成一个圆柱体,下面的哪一个圆柱体是左边的长方形卷成的?
把2米长的圆柱形木条截成三段小圆柱形木条,表面积增加8平方分米,这根圆柱形木条原来的体积是多少立方分米?
一个圆柱的侧面沿高展开后是一个长12.56cm,宽6.28cm的长方形,求这个圆柱的底面半径。
一个圆柱形水槽,底面半径是8厘米,水槽中完全浸没着一块铁件,当铁件取出时,水面下降了5厘米。这块铁件的体 积是多少立方厘米?
课后作业
一个圆柱的底面半径是4dm,高是7dm,它的侧面积是( )dm?。
一个圆柱的侧面积是18.84m?,高是3m,它的底面积是( )m?。
一个圆柱与一个圆锥等底等高,圆锥的体积是19.2cm?,则圆柱的体积比圆锥的体积多( )cm?。
等底等高的圆柱和圆锥,已知它们的体积之差是24 dm?,则圆柱的体积是( )dm?。
一个圆柱和一个圆锥的底面积相等,体积也相等。圆柱的高是6dm,圆锥的高是( )dm。
① V=S h只能求圆柱的体积。( )
② 如果一个圆锥和一个圆柱的体积相等,底面积也相等,那么它们的高也一定相等。( )
③ 把一个底面积是4dm?,高是4dm的大圆柱截成4个相同的小圆柱,其表面积增加了24dm?。( )
④ 圆柱的侧面展开图可以是一个梯形。( )
⑤ 圆柱和圆锥都有无数条高。( )
[单选题] 求压路机的前轮转动一周能压多少路面就是求压路机前轮的( )。A.侧面积 B.表面积 C.体积
[单选题] 一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的( )倍。
B.4 C.6
[单选题] 一个圆锥的体积是3m?,底面积是3m?,它的高是( )m。
505825526214B.1 C.
[单选题] 在棱长是8cm的正方体上面的正中央向下挖一个底面直径是2cm,高是2cm的圆柱,则正方体的表面积增加
的部分是所挖圆柱的( )。
A.侧面积 B.侧面积+一个底面积 C.表面积
[单选题] 一个圆柱和一个圆锥的底面积相等,圆柱的高是圆锥的高的2倍,圆锥的体积是圆柱体积的(
)。
505825525674A. B. C.
368300401187计算下图的体积。(单位:cm)
一种圆柱形通风管的底面直径是8dm,长是60dm。制作12节这样的通风管至少需要多少平方米铁皮?
孔庙大成殿前檐有10根石雕圆柱,高约6m,直径约1m。如果每立方米石料重2.7吨,这些柱子约重多少吨?
一个圆锥形沙堆的底面周长是12.56m,高是1.8m。用这堆沙子在8m宽的公路上铺3cm厚的路面,能铺多少米?
373709406858一根长2m,横截面半径是20cm的木头浮在水面上,何小泉发现它正好是一半露出水面(如图),你知道这根木头露 出水面的面积是多少吗?
2532894157139
1、完成本堂课的课后作业;
2、把题目的关键字圈出,想清楚问题问的是什么,再开始做题;
3、本堂课中的错题誊写到错题本上,下节课会对错题进行练习。
课首小测
1.2;1;完全相等;无数;相等。
2.1;1;扇形;顶点;底面圆心;1。
3.圆柱的表面积:S表=S侧+2 S底=Ch+2πr?;圆柱的体积:V柱=S底h=πr? h,圆锥的体积:V锥=S底h= πr? h。
导学一
知识点讲解 1:圆柱与圆锥的组成及其特征例题
错
错
解析:圆柱的侧面只有沿着高剪开时,展开图才是一个长方形(或正方形)。3.①; ③; ②; ①。
4.错
解析:圆柱侧面展开图的一边是高(d),一边是底面周长(πd),d≠πd,所以侧面展开图不是正方形。 5.对
解析:圆柱的侧面展开图是一个正方形,高=底面周长=πd,底面直径:高=d:πd=1:π。
我爱展示
1.C
解析:沿着圆柱的高展开,可得到正方形或长方形,沿着斜边展开可得到平行四边形,但得不到梯形。2.错
解析:圆锥的侧面展开图是扇形,而半圆也是扇形,因此半圆能围成圆锥。3.大小完全一样;圆;等腰三角形。
4.6.28;1。
解析:圆柱的侧面展开图是一个正方形,底面周长=高=6.28cm;底面半径=C÷2π=6.28÷2÷3.14=1(cm)。 5.错
解析:圆柱的侧面展开图是一个正方形,高=底面周长=πd,高÷底面直径=πd÷d=π。
导学二
知识点讲解 1:圆柱(与圆锥)的表面积例题
1.① 求一个侧面积和两个底面积;② 求一个侧面积;③ 求一个侧面积和一个底面积。
2.1004.8
解析:h= d= ×8=6(米), r=d= ×8=4(米), S侧=πdh=3.14×8×6=150.72(平方米), S底=πr?=3.14×4?=50.24(平方米), (150.72+50.24)×5=1004.8(千克)
3.56平方米
解析:圆柱的高和直径就是正方体的棱长,d=h=2分米 S侧=πdh=3.14×2×2=12.56(平方分米)
4.6平方米
解析:每分钟压路多少平方米,就是求每分钟压了多少个侧面积。 S侧=Ch=2πrh=2×3.14×1×2×10=125.6(平方米)
答:这台压路机的前轮每分钟压过的路面的面积是125.6平方米。5.100.48cm?
解析:S侧=2(r h=2×3.14×r?=50.24,r?=50.24÷2÷3.14=8(cm?), S表= S侧+2 S底=50.24+2×3.14×8=50.24+50.24=100.48(cm?)
答:圆柱体的表面积是100.48cm?。6.94.2m?
解析:S侧1+S侧2+S侧3+2 S底=2×3.14×(1+2+3)+2×3.14×3?=37.68+56.52=94.2(m?) 答:这个物体的表面积是94.2m?。
7.48dm?
解析:长方形的长由圆的直径和底面周长组成, d+πd=16.56,d=16.56÷(1+π)=16.56÷4.14=4(dm)
高由两个相等的圆的直径组成,
S侧=Ch=πd×2d=3.14×4×2×4=100.48(dm?) 答:这个圆柱的侧面积是100.48dm?。
我爱展示
1.3;2;1。
2.301
解析:笔筒的表面积由一个侧面和一个底面组成,
S表=S侧+S底=2πrh+πr?=2×3.14×4×10+3.14×4?=251.2+50.24=301.44≈301(平方厘米) 3.37.68米;113.04平方米。
解析:每分钟前进多少米,就是求每分钟转了多少个周长。3.14×1.2×10=37.68(米)
每分钟压路多少平方米,就是求每分钟压了多少个侧面积。37.68×3=113.04(平方米) 答:每分钟压路机前进37.68米,每分钟压路113.04平方米。
4.B
解析:切成3个小圆柱,就是切了2刀,增加了(3-1)×2=4(面),S底=3.6÷4=0.9(dm?) 5.31.4dm?
解析:长方形的长由圆的直径和底面周长组成,d+πd=8.28,d=8.28÷(1+π)=8.28÷4.14=2(dm) 高由两个相等的圆的直径组成,h=2d=2×2=4(dm),r=d÷2=2÷2=1(dm)
S表=S侧+2 S底=πdh+2πr?=3.14×2×4+2×3.14×1?=25.12+6.28=31.4(dm?) 答:所制汽油桶的表面积是31.4dm?。
知识点讲解 2:圆柱与圆锥的体积例题
1.4710立方厘米
解析:V柱=S底h=πr? h=3.14×10?×15=4710(立方厘米) 答:它的体积是4710立方厘米。2.50.24立方米
解析:r=d÷2=4÷2=2(米)
V=V锥+V柱= S底h+S底h= S底h= ×3.14×2?×3=50.24(立方米) 3.33.912吨
解析:V锥= S底h= ×3.14×3?×2=18.84(立方米),18.84×1.8=33.912(吨)答:这堆沙重33.912吨。4.226.08立方厘米和75.36立方厘米
解析:以长为半径,宽为高:V柱1=3.14×6?×2=226.08(立方厘米) 以宽为半径,长为高:V柱2=3.14×2?×6=75.36(立方厘米)
答:转一周所得到的圆柱体的体积是226.08立方厘米和75.36立方厘米。5.18.84立方厘米;12.56立方厘米。
解析:V1=3.14×3?×2÷3=18.84(立方厘米); V2=3.14×2?×3÷3=12.56(立方厘米)
答:较大圆锥体的体积是18.84立方厘米,较小的圆锥体体积是12.56立方厘米。6.3:1;40。
18576152333372292384233337解析:削成的圆锥与圆柱等底等高,根据公式V柱=S底h,V锥= S底h,V柱:V锥=3:1;
削掉部分的体积: V柱= ×60=40(立方分米)。
7.错
1709609284048解析:已知V柱:V锥=1:1,h柱:h锥=1:1;根据公式V柱=S底h,V锥= S底h,得:
圆柱的S底×h= 圆锥的S底×h → 3圆柱的S底=圆锥的S底→ 圆锥的S底=3×12=36(cm?)。
8.14.4
解析:已知V柱:V锥=1:9,圆柱与圆锥的底面积相等;根据公式V柱=S底h,V锥= S底h,得:
V柱=9 V锥→ S底×h柱=9××S底×h锥 → h柱=3 h锥 → h柱=3×4.8=14.4(厘米)。
我爱展示
1.301.44;100.48;6.28;1413。
解析:V1=3.14×4?×6=301.44(立方厘米);V2=3.14×( )?×8=100.48(立方厘米); V3=3.14×( )?×2=6.28(立方分米);V4=3.14×( )?×4.5=1413(立方米)。2.10.99cm?
解析:r=d÷2=2÷2=1(cm),V=V柱-V锥=3.14×1?×4- ×3.14×1?×1.5=12.56-1.57=10.99(cm?)。3.56.52
解析:圆锥的底面直径和高等于正方体的棱长,V锥= S底h= ×3.14×( )?×6=56.52(立方厘米) 4.36
解析:圆柱和圆锥等体等底的情况下,根据公式V柱=S底h,V锥= S底h,得:
S底×h柱= S底×h锥 → h柱= h锥 → h锥=3 h柱=3×12=36(cm)。5.50.24立方厘米
解析:V1=3.14×4?×2=100.48(立方厘米), V2=3.14×2?×4=50.24(立方厘米) V1-V2=100.48-50.24(立方厘米)
6.7.536吨
解析:r=18.84÷2÷3.14=3(米), ×3.14×3?×1×0.8=7.536(吨) 答:这堆稻谷重7.536吨。
知识点讲解 3:圆柱与圆锥的表面积与体积的应用例题
1.0.625米
解析:V锥= ×37.5×2=25(立方米), h=25÷8÷5=0.625(米) 答:可以铺0.625米厚。
2.50天
解析:8毫米=0.8厘米,15毫米=1.5厘米,r=d÷2=0.8÷2=0.4(厘米)
V柱=3×0.4×0.4×1.5=0.72(立方厘米),72÷2÷0.72=50(天)答:这盒牙膏大约能供她使用50天。3.100.48平方分米
解析:增加的是两个圆形的底面积,2 S底=2×3.14×4?=100.48(平方分米) 答:表面积增加了100.48平方分米。
4.120平方分米
解析:增加的是两个长方形的面积,长方形的长是圆柱的高,长方形的宽是圆柱的底面直径
1米=10分米,d=2r=2×3=6(分米),S长=2×10×6=120(平方分米) 答:表面积增加了120平方分米。
5.251.2立方厘米
372307241795解析:如下图所示,用两个原来的立体图形拼成一个圆柱体,圆柱体的底面积不变,h=4+6=10(厘米)
r=25.12÷2÷3.14=4(厘米),V= V柱= ×3.14×4×4×10=251.2(立方厘米) 答:截去后剩下的体积是251.2立方厘米。
6.157
373094455172解析:画图观察,如果高截短了2厘米,两个底面积没有变化,虚线表示表面积减少的部分是一个长方形, 长方形的长是底面周长,宽是减少的2厘米。
根据S长=长×宽,可得:C=62.8÷2=31.4(厘米), r=31.4÷2÷3.14=5(厘米) V减=πr? h减=3.14×5?×2=157(立方厘米)
7.7.693立方分米
解析:V石=V升=πr? h升=3.14×3.5×3.5×0.2=7.693(立方分米) 答:这块石头的体积是7.693立方分米。
8.116.18立方厘米
解析:15.7÷1=15.7(立方厘米),V球=3.14×4×4×(10-8)+15.7=116.18(立方厘米) 答:小铁球的体积是116.18立方厘米。
9.1750克
解析:剩下的油和原来的油的体积相似,现在油的高度和原来油的高度比是1:2,那么它们的体积比是1:8, 即剩下的油的体积是原来的油的体积的 。米老鼠偷走了1- = ,2000× =1750(克)
答:米老鼠共偷得香油1750克。
我爱展示
1.24平方厘米
解析:V锥=V长=abh=6×4×5=120(立方厘米),S底=3 V锥÷h=3×120÷15=24(平方厘米) 答:这个圆锥的底面积是24平方厘米。
2.100.48立方厘米
解析:截成4段,就是切了3刀,(4-1)×2=6(面),S底=75.36÷6=12.56(平方厘米) V柱=S底h=12.56×8=100.48(立方厘米)
答:原木材体积是100.48立方厘米。3.100.48立方厘米
解析:增加的面积展开来是一个长方形,长方形的长是底面周长,宽是增加的2厘米。
根据S长=长×宽,可得:C=25.12÷2=12.56(厘米), r=12.56÷2÷3.14=2(厘米)
V柱=πr? h=3.14×2?×8=100.48(立方厘米) 答:原来圆柱的体积是100.48立方厘米。4.376.8立方厘米
解析:表面积增加的部分是两个以底面直径为底边,以圆锥的高为高的等腰三角形, S△=120÷2=60(平方厘米),h=2×60÷12=10(厘米),r=d÷2=12÷2=6(厘米) V锥= ×3.14×6×6×10=376.8(立方厘米)
答:这个圆锥形木块的体积是376.8立方厘米。
5.0.6厘米
解析:玻璃杯是是圆柱形的,铅锤取出后水面下降部分实际是一个小圆柱,这个圆柱的底面与玻璃杯的底面一样,是一个 直径为20厘米的圆,它的体积正好等于圆锥形铅锤的体积,小圆柱的高就是水面下降的高度。
V锥= ×3.14×( )?×20=188.4(立方厘米),S底=3.14×( )?=314(平方厘米)
h降=188.4÷314=0.6(厘米) 答:杯里的水将下降0.6厘米。
限时考场模拟
1.(1)×;(2)×;(3)√
2.①和③
解析:分析:如果用长方形长12.56cm作圆柱底面周长,则底面直径是12.56÷3.14=4(cm),高是3.14cm; 如果用长方形宽3.14cm作圆柱底面周长,则底面直径是3.14÷3.14=1(cm),高是12.56cm。
3.40立方分米
解析:h=2米=20分米,截成三段,增加了(3-1)×2=4(面),S底=8÷4=2(平方分米);
V柱=S底h=2×20=40(立方分米)。 答:这根圆柱形木条原来的体积是40立方分米。4.2cm或1cm
解析:如果以12.56cm 作为底面周长,r1=12.56÷2÷3.14=2(cm) 如果以6.28cm作为底面周长,r2=6.28÷2÷3.14=1(cm)
答:这个圆柱的底面半径是2cm或1cm。5.1004.8立方厘米
解析:V铁=S底h降=3.14×8×8×5=1004.8(立方厘米)答:这块铁件的体积是1004.8立方厘米。
课后作业
1.175.84
解析:S侧=2×3.14×4×7=175.84(dm?) 2.3.14
解析:r=18.84÷3÷2÷3.14=1(m), S底=3.14×1×1=3.14(m?) 3.38.4
解析:等底等高的圆柱与圆锥的体积比是3:1,V柱=3 V锥=3×19.2=57.6(cm?) 57.6-19.2=38.4(cm?)
4.36
解析:等底等高的圆柱与圆锥的体积比是3:1,V柱=24÷(3-1)×3=36(dm?) 5.18
解析:根据已知条件得:V柱=V锥,S底h柱= S底h锥 → h锥=3 h柱=3×6=18(dm)
6.(1)×;(2)×;(3)√;(4)×;(5)×
7.A
8.B
9.A
解析:h=3 V锥÷S底=3×3÷3=3(m) 10.A
11.C
解析:V锥= Sh, V柱=S×2h=2Sh, V锥÷V柱= Sh÷2Sh= 。12.1256cm?
解析:r=6÷2=3(cm),R=10÷2=5(cm),V=S环h=3.14×(5?-3?)×25=1256(cm?) 13.180.864平方米
解析:8分米=0.8米,60分米=6米,S侧×12=πdh=3.14×0.8×6×12=180.864(平方米) 答:制作12节这样的通风管至少需要180.864平方米铁皮。
14.127.17吨
解析:r=1÷2=0.5(米),V柱=3.14×0.5×0.5×6=4.71(立方米),4.71×10×2.7=127.17(吨) 答:这些柱子约重127.17吨。
15.31.4米
解析:r=12.56÷2÷3.14=2(米), V锥=×3.14×2×2×1.8=7.536(立方米) 3厘米=0.03米, 7.536÷8÷0.03=31.4(米)
答:能铺31.4米。16.138.16平方米
解析:2米=20分米,20厘米=2分米,S表=S侧+2 S底=2×3.14×2×20+2×3.14×2×2=276.32(平方米) 276.32÷2=138.16(平方米)
368300187563答:这根木头露出水面的面积是138.16平方米。
