人教版小学数学六年级下册讲义 圆锥的认识和体积;圆柱和圆锥体积的应用(含答案)
文档属性
| 名称 | 人教版小学数学六年级下册讲义 圆锥的认识和体积;圆柱和圆锥体积的应用(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 278.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 00:00:00 | ||
图片预览





文档简介
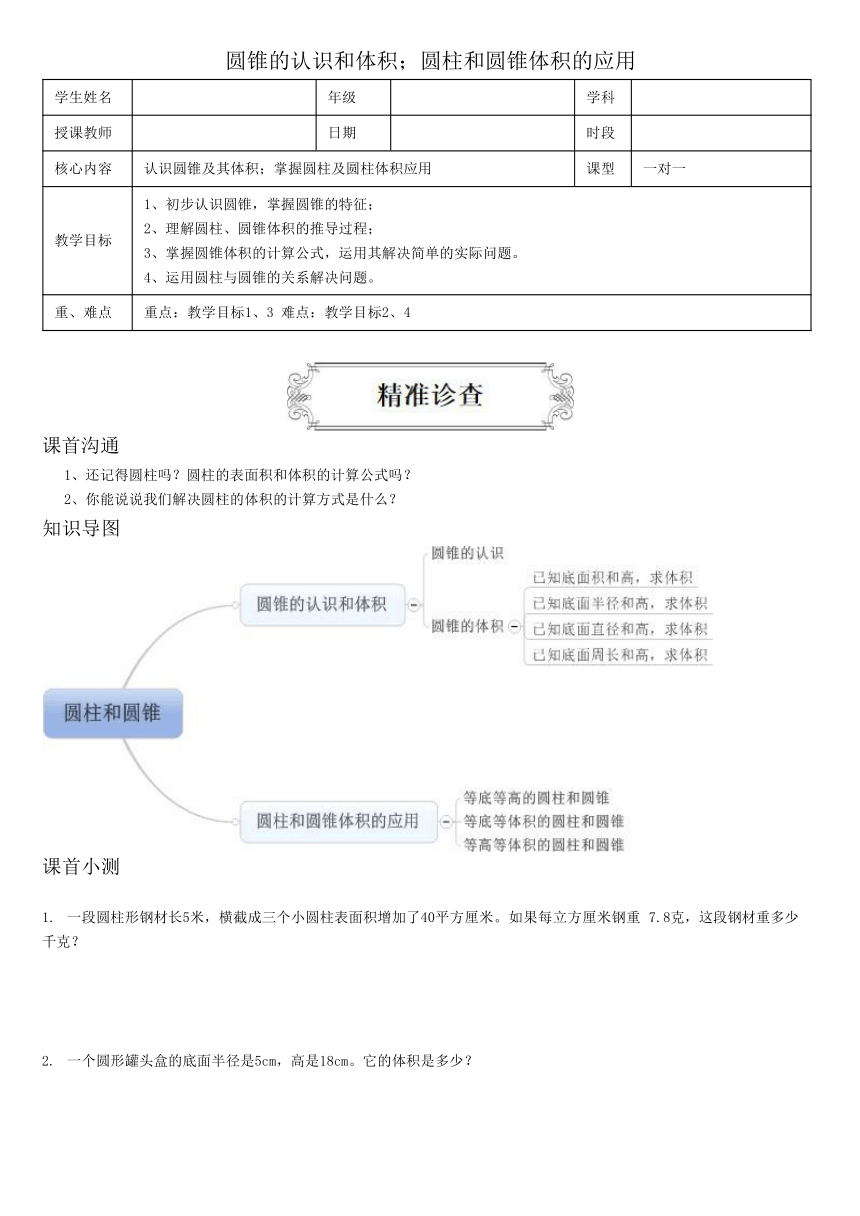
圆锥的认识和体积;圆柱和圆锥体积的应用
学生姓名
年级
学科
授课教师
日期
时段
核心内容
认识圆锥及其体积;掌握圆柱及圆柱体积应用
课型
一对一
教学目标
1、初步认识圆锥,掌握圆锥的特征;
2、理解圆柱、圆锥体积的推导过程;
3、掌握圆锥体积的计算公式,运用其解决简单的实际问题。
4、运用圆柱与圆锥的关系解决问题。
重、难点
重点:教学目标1、3 难点:教学目标2、4
2532894114879
课首沟通
1、还记得圆柱吗?圆柱的表面积和体积的计算公式吗?
2、你能说说我们解决圆柱的体积的计算方式是什么?
387246334977知识导图
课首小测
一段圆柱形钢材长5米,横截成三个小圆柱表面积增加了40平方厘米。如果每立方厘米钢重 7.8克,这段钢材重多少千克?
一个圆形罐头盒的底面半径是5cm,高是18cm。它的体积是多少?
导学一 : 圆锥的认识和体积
知识点讲解 1:圆锥的认识
圆锥是由一个底面和一个侧面两部分组成的。
418097493965(1)底面:圆锥中圆形的面就是它的底面,它有一个底面。底面的圆心、半径、直径和周长分别叫做圆锥的底面圆心、底 面半径、底面直径和底面周长,分别用字母O、r、d和C表示。
侧面:圆锥周围的面就是它的侧面。圆锥的侧面是一个曲面
5746035-431440高:从圆锥的顶点到底面圆心的距离 就是圆锥的高,高用字母h表示。圆锥只有一条高。
例 1. 圆锥的底面是一个( );侧面是一个( ),侧面展开是一个( )。例 2. 圆锥的高是指从圆锥( )到底面( )的( )。
【学有所获】测量圆锥的高:“先把圆锥的底面放平,用一块平板水平地放在圆锥的顶点上面,竖直地量出平板和底面 之间的距离。”
我爱展示
圆锥有( )条高
371752191264画出下列每个圆锥的高
知识点讲解 2:圆锥的体积
一个圆锥所占空间的大小,叫做这个圆锥的体积。
圆锥的体积的计算公式:圆锥的体积=底面积×高× V圆锥= Sh
2181380258650推导公式:圆柱的体积=底面积×高,与圆柱等底等高的圆锥的体积等于圆柱体积的 , 推得圆锥的体积=底面积×高×
例 1. 如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?(单位:cm)
【学有所获】同底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍。
例 2. (2013年海珠区六年级数学单元检测卷)一个圆锥形容器,底面半径是2dm,高3dm。把它装满水,然后全部倒入一个底面半径为1dm的圆柱形空容器中(未装满),圆柱形容器的水深多少分米?
例 3. 一个圆锥的底面直径是5dm,高是4dm,求圆锥的体积。(得数保留两位小数)
我爱展示
[单选题] 一个圆锥的高不变,底面积扩大到原来的3倍,则它的体积( )
A.扩大到原来的3倍 B.缩小到原来的 C.不变
计算下面各圆锥的体积。
(1)底面直径是4dm,高是6dm。 (2)底面半径是 3cm,高是2dm。 (3)底面周长是6.28m,高是1.5m。
导学二 : 圆锥体积计算公式的应用
知识点讲解 1:已知圆锥的底面积和高,求圆锥的体积。
直接利用圆锥的体积计算公式V= Sh进行计算
例 1. 一个圆锥形铁锤的底面积是24cm?,高是8cm。这个铁锤的体积是多少立方厘米?
知识点讲解 2:已知圆锥的底面半径和高,求圆锥的体积。
例 1. 求右边圆锥的体积。(单位:cm)。
知识点讲解 3:已知圆锥的底面直径和高,求圆锥的体积。
已知圆锥的底面直径和高,可以直接利用公式V= π( )?h来求圆锥的体积
2838350401271例 1. 工地上有一堆沙子,近似于一个圆锥(如右图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?(得数保留两位小数)
知识点讲解 4:已知圆锥的底面周长和高,求圆锥的体积。
5983296469886计算时先根据公式S=π( )?(求出圆锥的底面积,再根据公式V= Sh求出圆锥的体积。
例 1. 天坛祈年殿塔的顶端近似于圆锥形,它的底面周长是18.84m,高是6m,求塔的顶端的体积。
我爱展示
李伯伯家种的小麦丰收了,他把小麦放在院子里堆成了圆锥形,底面周长是12.56m,高是1.5m。如果每立方米小麦重
750kg,这堆小麦重多少千克?
一个近似圆锥形的稻谷堆,底面周长是9.42m,高是1.2m。每立方米稻谷大约重730千克,把这些稻谷装进袋子里,每 袋装90千克,需要多少个袋子?
沙漏是两个完全相同的圆锥形容器的组合体,单个圆锥形容器高6cm,漏口每秒可漏细沙0.05cm?,漏完全部细沙用时
3683002439395分钟,这个沙漏的底面积是多少平方厘米?
导学三 : 圆柱和圆锥体积的应用
知识点讲解 1:等底等高的圆柱和圆锥:圆锥的体积等于和它等底等高的圆柱体积的。
2310885304901圆柱的体积比圆锥的体积多2倍;圆锥的体积比圆柱的体积少 。等底等高的圆柱和圆锥的体积比:
例 1. 一个圆柱的底面半径是3cm,高是2cm,与它等底等高的圆锥的体积是( )cm?。
知识点讲解 2:等底等体积的圆柱和圆锥:圆锥的高是圆柱的高的3倍,或者说圆锥的高比圆柱的高多2 倍;圆柱的高是圆锥的高的 ,或者说圆柱的高比圆锥的高少 。
例 1. 圆柱的高是3cm,与它等底等体积的圆锥的高是9cm。( )
知识点讲解 3:
等高等体积的圆柱和圆锥:圆锥的底面积是圆柱的底面积的3倍,或者说圆锥的底面积比圆柱的底面积多2倍;圆柱的底 面积是圆锥的底面积的 ,或者说圆柱的底面积比圆锥的底面积少 。
例 1. (2013年海珠区单元测试题)一个圆柱与一个圆锥体积相等,高也相等,圆柱的底面积是12cm?,那么圆锥的底面积是4cm?。( )
我爱展示
一个圆柱体和一个圆锥体的体积相等,它们的底面积的比是3:5,圆柱的高8厘米,圆锥的高是( )厘米。
把一个体积是120cm?的圆柱形木材削成一个最大的圆锥,则削去部分的体积是( )cm?
(2010年广州市大联盟小升初试题)一个圆柱体和一个圆锥体等底等高,他们的体积和是72立方分米,圆锥的体积是
( )立方分米,圆柱体的体积是( )立方分米。4. 等底等高的正方体、长方体的和圆柱的体积都相等( )
圆柱体的体积与圆锥体的体积比是3:1。( )
等体积等高的圆柱和圆锥:圆柱的底面积是圆锥的底面积的3倍。( )
692063193701计算下列圆柱的体积。
2699401-166506(1) (2)
一个圆柱形鱼缸,底面直径是40cm,高是25cm,里面盛了一些水,把一个底面半径为10cm的圆锥放入鱼缸中(圆锥全 部浸入水中),鱼缸中的水面升高了2cm。这个圆锥的高是多少?
2532894266735
限时考场模拟
1.
等底等高的圆柱和圆锥,圆柱的体积是圆锥的(
),圆锥的体积是圆柱的(
),圆柱的体积比圆锥大
(
),圆锥的体积比圆柱小( )。
一个圆柱和一个圆锥的体积都是24.6立方分米,底面积都是6平方分米,那么圆柱的高是( )分米,圆锥的高是( )分米。
(2014年天河区小升初数学招生试卷).一个圆柱与一个圆锥体积相等,底面积也相等。已知圆柱的高是12cm,圆锥 的高是( )cm。
课后作业
(2012年大联盟小升初试题)一个圆锥与一个圆柱的底面积相等,已知圆锥与圆柱的体积比是1:9,圆锥的高是4.8 厘米,则圆柱的高是( )厘米。
一个圆锥的体积是10.8立方米,与它等底等高的圆柱的体积是( )。
一个圆锥的体积是50.24立方米,底面半径是2米,它的高是( )米。
一个圆柱的底面半径是3分米,高2分米,体积是( )立方分米
一个圆锥体,底面直径和高都是3cm,它的体积是( )立方厘米
一个圆锥的体积是75.36dm?,底面半径是3dm,它的高是( )dm
V=Sh只能求圆柱的体积( )
圆柱和圆锥都有无数条高。( )
一个圆锥的底面半径扩大到原来的5倍,它的体积也扩大到原来的25倍。( )
[单选题] 同底等高的圆柱体的体积是圆锥体积的( )
A.3倍 B. C.无法确定
11. [单选题]
将一个圆柱体铝块熔铸成圆锥体,它的(
)不变。
A.表面积
B.体积
C.底面积
12. [单选题] 一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的( )被。
A.2 B.4 C.6
13.
[单选题]
一个圆锥的体积是3m?,底面积是3㎡,它的高是(
)m。
A.3
B.1
C.
5123008434202
[单选题] (2013年广州市小联盟数学试题)把底面积是18平方厘米,高是2厘米的圆柱形零件削成最大的圆锥体, 削成的最大圆锥体的体积是( )立方厘米
A.12 B.18 C.24 D.36
70131445955419485313366964022210246792计算下图的体积。(单位:cm)
(1) (2) (3)
一个圆柱体和一个圆锥体等底等高,它们的体积相差50.24立方厘米。如果圆锥体的底面半径是2厘米,这个圆锥体 的高是多少厘米?
一个圆锥形沙堆,它的底面周长是12.56m,高是1.8m。用这堆沙子在8m宽的公路上铺3cm厚的路面,能铺多少米?
有一囤稻谷,上面是圆锥形,下面是圆柱,量得圆柱的底面周长是6.28米,高是2米,圆锥的高0.3米,这囤稻谷重 多少千克?(每立方米稻谷重650千克)
(2014年广州市小联盟数学试题)唐老鸭用一个圆锥形容器装满了2000克香油,米老鼠趁唐老鸭不在,在容器的中 间咬了一个洞,然后开始偷油,一直偷到油面与小洞平齐为止(如图)。问:米老鼠共偷得香油多少克(容器的厚度不 计)?
2532894112798
1、学完这节课的内容后,回去复习圆锥和圆柱的知识。
2、标注理解不够深刻的例题及时复习整理。
3、总结圆柱与圆锥的体积应用题。
4、整理课堂上做错的习题到错题本上,课下及时完成相应练习。
2532894211904
课首小测
1.39千克。
解析:5米=500厘米
40÷4×500×7.8=39000(克)
=39(千克) 答:这段钢材重39千克。
2.1413cm?。
解析:3.14×5?×18
=3.14×25×18
=1413(cm?)
答:它的体积是1413 cm?。
导学一
知识点讲解 1:圆锥的认识例题
圆;曲面;扇形
顶点;圆心;垂直距离
我爱展示
5012262619501.1
2.
知识点讲解 2:圆锥的体积
例题
1.4cm
解析: ×12=4(cm)
答:这时乙容器中的水有4cm。2.4分米
解析: ×3.14×2?×3÷(1?×3.14)=4(分米)
答:圆柱形容器的水深4分米。3.26.17dm?
解析: ×[3.14×(5÷2)?]×4≈26.17(dm?)
答:圆锥的体积约为26.17 dm?。
我爱展示
1.A
解析: 圆锥的体积=底面积×高× ,当底面积扩大3倍时,
圆锥现在的体积=(底面积×3)×高× ,即3倍圆锥原来的体积。所以选扩大到原来的3倍。2.(1)25.12dm?;(2)188.4cm?;(3)1.57m?
解析:(1) ×3.14×(4÷2)?×6=25.12(dm?)
(2)2dm=20cm ×3.14×3?×20=188.4(cm?)
(3) ×3.14×(6.28÷3.14÷2)?×1.5=1.57(m?)
导学二
知识点讲解 1:已知圆锥的底面积和高,求圆锥的体积。例题
1.64cm?。
解析: ×24×8=64(cm?)
答:这个铁锤的体积是64cm?
知识点讲解 2:已知圆锥的底面半径和高,求圆锥的体积。例题
1.113.04cm?。
解析: 3.14×3?=28.26(cm?) ×28.26×12=113.04(cm?)
答:这个圆锤的体积是113.04cm?
知识点讲解 3:已知圆锥的底面直径和高,求圆锥的体积。例题
1.5.02m?;7.53t。
解析:(1)沙堆的底面积:3.14×(4÷2)?
=3.14×4
=12.56(m?)
(2)沙堆的体积: ×12.56×1.2
=12.56×0.4
=5.024(m?)
≈5.02(m?)
(3)沙堆的质量:5.02×1.5=7.53(t)
答:这堆沙子的体积大约是5.03m?,大约重7.53t。
知识点讲解 4:已知圆锥的底面周长和高,求圆锥的体积。例题
1.56.52m?。
解析: 圆锥的底面积:3.14×(18.84÷3.14÷2)?
=3.14×9
=28.26(m?)
圆锥的体积: ×28.26×6
=2×28.26
=56.52(m?)。答:塔的顶端的体积是56.52m?
我爱展示
1.4710千克
解析: ×3.14×(12.56÷3.14÷2)? ×1.5×750=4710(kg)
答:这堆小麦重4710千克。
2.23个
解析:3.14×(9.42÷3.14÷2)?×1.2× ×730÷90≈23(个)
答:需要23个袋子。3.7.5平方厘米
解析: 0.05×(5×60)÷ ÷6=7.5(cm?)
答:这个沙漏的底面积是7.5平方厘米。
导学三
知识点讲解 1:等底等高的圆柱和圆锥:圆锥的体积等于和它等底等高的圆柱体积的。例题
1.18.84。
解析: 因为圆锥的体积等于和它等底等高的圆柱体积的 ,所以圆锥的体积= ×圆柱的体积即 ×3.14×3?×2=18.84(cm?)
知识点讲解 2:等底等体积的圆柱和圆锥:圆锥的高是圆柱的高的3倍,或者说圆锥的高比圆柱的高多2倍;圆柱的高是圆锥的高的 ,或者说圆柱的高比圆锥的高少 。
例题
1.对
解析:因为等底等体积的圆柱和圆锥,圆锥的高是圆柱的高的3倍;圆柱的高是3cm,圆锥的高是9cm;故此题判断对。
知识点讲解 3: 例题
1.错
266240090620380020090620544677290620627930944370解析:因为等高等体积的圆柱和圆锥中, , ;根据公式 , ,
得:
244039135464圆柱的底面积×圆柱的高= 圆锥的底面积×圆锥的高 → 3倍圆柱的底面积=圆锥的底面积 → 圆锥的底面积
=3×12=36(cm?)。
我爱展示
1.14.4厘米
110833290699470673990699解析: 已知 ,圆柱与圆锥的底面积之比是3:5;根据公式 , ,得:
95107573916→
=14.4(厘米)。
→
圆锥的高= 2.80
解析: 把一个圆柱削成一个最大的圆锥,这个圆锥与圆柱等底等高,所以
削去部分的体积=圆柱的体积-圆锥的体积
且等底等高的圆锥的体积等于圆柱体积的 即削去部分的体积=120- ×120=80(cm?)
3.18;54
解析: 等底等高的圆柱和圆锥的体积比: 所以圆锥的体积:72÷(1+3)=18(立方分米)
圆柱的体积:72-18=54(立方分米)
对
错
解析:等底等高的圆柱和圆锥的体积比: ,故判断为错6.错
解析:等体积等高的圆柱和圆锥:圆柱的底面积是圆锥的底面积的 倍。故判断为错。7.(1)1130.4cm?;(2)251.2cm?
解析:(1)3.14×6?×10=1130.4(cm?);(2)3.14×( )?×20=251.2(cm?) 8.24cm
解析: 3.14×(40÷2)?×2×3÷(3.14×10?)
=7536÷314
=24(cm)
答:这个圆锥的高是24cm。
限时考场模拟
1.3倍; ;2倍;
2.4.1;12.3
解析: 圆锥的体积= ×底面积×高;圆锥的高=圆锥的体积×3÷底面积, 所以圆锥的高是:24.6×3÷6=12.3(分米)
圆柱的体积=底面积×高;圆柱的高=圆柱的体积÷底面积, 即 圆柱的高是:24.6÷6=4.1(分米)
3.36
解析: 本题主要考察了圆柱和圆锥等体等底的情况下,它们的高的关系的知识点。圆柱和圆锥等体等底的情况下,圆锥的高是圆柱高的3倍,所以12×3=36。
课后作业
1.14.4
110833290699438297590699解析: 已知 ,圆柱与圆锥的底面积相等;根据公式 , ,得:
95107564676388345464676→ →
圆柱的高=3×4.8=14.4(厘米)。2.32.4立方米
解析: 等底等高的圆柱和圆锥,圆柱的体积是圆锥的体积的3倍
即 圆柱的体积=圆锥的体积×3=10.8×3=32.4(立方米)
3.12
解析: 圆锥的体积=底面积×高,圆锥的高=圆锥的体积÷ ÷底面积即 圆锥的高:50.24÷ ÷(3.14×2?)=12(米)
4.56.52
解析:3.14×3?×2=56.52(立方分米) 5.7.065
解析: ×3.14×(3÷2)?×3=7.065(立方厘米)
6.8
解析:75.36÷ ÷(3.14×3?)=8(dm) 7.错
解析:不只是圆柱的体积=底面积×高8.错
解析:圆柱有无数条高,但是圆锥只有一条高。9.对
解析:圆锥的体积= ×底面积×高,底面半径扩大5倍,底面半径就扩大25倍,圆锥的体积也扩大25倍,故判断为√。
10.A
解析: 因为圆锥的体积= ×底面积×高,圆柱的体积=底面积×高,所以同底等高的圆柱体的体积是圆锥体的3倍。11.B
12.B
13.A
解析: 圆锥的体积= ×底面积×高,高=圆锥的体积÷ ÷底面积=3÷ ÷3=3(m) 14.A
解析:圆锥的体积: ×18×2=12(立方厘米) 15.(1)25.12cm?;(2)10.99cm?;(3)9.57cm? 解析:(1) ×3.14×2?×6=25.12(cm?);
(2)3.14×(2÷2)?×4- ×3.14×(2÷2)?×1.5=10.99(cm?);
(3)2×2×2+3.14×(1÷2)?×2=9.57(cm?) 16.6厘米
解析:等底等高的圆柱和圆锥体,圆柱的体积比圆锥的体积多2倍。圆锥的体积:50.24÷2=25.12(立方厘米)
圆锥体的高:25.12×3÷(3.14×2?)
=75.36÷12.56
=6(厘米) 答:这个圆锥体的高是6厘米。
17.31.4米
解析:3cm=0.03m ×3.14×(12.56÷3.14÷2)?×1.8÷(8×0.03)=31.4(米)
答:能铺31.4米。18.4286.1千克
解析:稻谷的体积: ×3.14×(6.28÷3.14÷2)?×0.3+3.14×(6.28÷3.14÷2)?×2=6.594(立方米)
稻谷的重量:6.594×650=4286.1(千克) 答:这囤稻谷重4286.1千克。
19.1750克
解析: 剩下的油和原来的油的体积相似,现在油的高度和原来油的高度比是1:2,那么它们的体积比是1:8,
即剩下的油的体积是原来的油的体积的 。米老鼠偷走了1- = ,2000× =1750(克) 答:米老鼠共偷得香油1750克。
学生姓名
年级
学科
授课教师
日期
时段
核心内容
认识圆锥及其体积;掌握圆柱及圆柱体积应用
课型
一对一
教学目标
1、初步认识圆锥,掌握圆锥的特征;
2、理解圆柱、圆锥体积的推导过程;
3、掌握圆锥体积的计算公式,运用其解决简单的实际问题。
4、运用圆柱与圆锥的关系解决问题。
重、难点
重点:教学目标1、3 难点:教学目标2、4
2532894114879
课首沟通
1、还记得圆柱吗?圆柱的表面积和体积的计算公式吗?
2、你能说说我们解决圆柱的体积的计算方式是什么?
387246334977知识导图
课首小测
一段圆柱形钢材长5米,横截成三个小圆柱表面积增加了40平方厘米。如果每立方厘米钢重 7.8克,这段钢材重多少千克?
一个圆形罐头盒的底面半径是5cm,高是18cm。它的体积是多少?
导学一 : 圆锥的认识和体积
知识点讲解 1:圆锥的认识
圆锥是由一个底面和一个侧面两部分组成的。
418097493965(1)底面:圆锥中圆形的面就是它的底面,它有一个底面。底面的圆心、半径、直径和周长分别叫做圆锥的底面圆心、底 面半径、底面直径和底面周长,分别用字母O、r、d和C表示。
侧面:圆锥周围的面就是它的侧面。圆锥的侧面是一个曲面
5746035-431440高:从圆锥的顶点到底面圆心的距离 就是圆锥的高,高用字母h表示。圆锥只有一条高。
例 1. 圆锥的底面是一个( );侧面是一个( ),侧面展开是一个( )。例 2. 圆锥的高是指从圆锥( )到底面( )的( )。
【学有所获】测量圆锥的高:“先把圆锥的底面放平,用一块平板水平地放在圆锥的顶点上面,竖直地量出平板和底面 之间的距离。”
我爱展示
圆锥有( )条高
371752191264画出下列每个圆锥的高
知识点讲解 2:圆锥的体积
一个圆锥所占空间的大小,叫做这个圆锥的体积。
圆锥的体积的计算公式:圆锥的体积=底面积×高× V圆锥= Sh
2181380258650推导公式:圆柱的体积=底面积×高,与圆柱等底等高的圆锥的体积等于圆柱体积的 , 推得圆锥的体积=底面积×高×
例 1. 如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?(单位:cm)
【学有所获】同底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍。
例 2. (2013年海珠区六年级数学单元检测卷)一个圆锥形容器,底面半径是2dm,高3dm。把它装满水,然后全部倒入一个底面半径为1dm的圆柱形空容器中(未装满),圆柱形容器的水深多少分米?
例 3. 一个圆锥的底面直径是5dm,高是4dm,求圆锥的体积。(得数保留两位小数)
我爱展示
[单选题] 一个圆锥的高不变,底面积扩大到原来的3倍,则它的体积( )
A.扩大到原来的3倍 B.缩小到原来的 C.不变
计算下面各圆锥的体积。
(1)底面直径是4dm,高是6dm。 (2)底面半径是 3cm,高是2dm。 (3)底面周长是6.28m,高是1.5m。
导学二 : 圆锥体积计算公式的应用
知识点讲解 1:已知圆锥的底面积和高,求圆锥的体积。
直接利用圆锥的体积计算公式V= Sh进行计算
例 1. 一个圆锥形铁锤的底面积是24cm?,高是8cm。这个铁锤的体积是多少立方厘米?
知识点讲解 2:已知圆锥的底面半径和高,求圆锥的体积。
例 1. 求右边圆锥的体积。(单位:cm)。
知识点讲解 3:已知圆锥的底面直径和高,求圆锥的体积。
已知圆锥的底面直径和高,可以直接利用公式V= π( )?h来求圆锥的体积
2838350401271例 1. 工地上有一堆沙子,近似于一个圆锥(如右图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?(得数保留两位小数)
知识点讲解 4:已知圆锥的底面周长和高,求圆锥的体积。
5983296469886计算时先根据公式S=π( )?(求出圆锥的底面积,再根据公式V= Sh求出圆锥的体积。
例 1. 天坛祈年殿塔的顶端近似于圆锥形,它的底面周长是18.84m,高是6m,求塔的顶端的体积。
我爱展示
李伯伯家种的小麦丰收了,他把小麦放在院子里堆成了圆锥形,底面周长是12.56m,高是1.5m。如果每立方米小麦重
750kg,这堆小麦重多少千克?
一个近似圆锥形的稻谷堆,底面周长是9.42m,高是1.2m。每立方米稻谷大约重730千克,把这些稻谷装进袋子里,每 袋装90千克,需要多少个袋子?
沙漏是两个完全相同的圆锥形容器的组合体,单个圆锥形容器高6cm,漏口每秒可漏细沙0.05cm?,漏完全部细沙用时
3683002439395分钟,这个沙漏的底面积是多少平方厘米?
导学三 : 圆柱和圆锥体积的应用
知识点讲解 1:等底等高的圆柱和圆锥:圆锥的体积等于和它等底等高的圆柱体积的。
2310885304901圆柱的体积比圆锥的体积多2倍;圆锥的体积比圆柱的体积少 。等底等高的圆柱和圆锥的体积比:
例 1. 一个圆柱的底面半径是3cm,高是2cm,与它等底等高的圆锥的体积是( )cm?。
知识点讲解 2:等底等体积的圆柱和圆锥:圆锥的高是圆柱的高的3倍,或者说圆锥的高比圆柱的高多2 倍;圆柱的高是圆锥的高的 ,或者说圆柱的高比圆锥的高少 。
例 1. 圆柱的高是3cm,与它等底等体积的圆锥的高是9cm。( )
知识点讲解 3:
等高等体积的圆柱和圆锥:圆锥的底面积是圆柱的底面积的3倍,或者说圆锥的底面积比圆柱的底面积多2倍;圆柱的底 面积是圆锥的底面积的 ,或者说圆柱的底面积比圆锥的底面积少 。
例 1. (2013年海珠区单元测试题)一个圆柱与一个圆锥体积相等,高也相等,圆柱的底面积是12cm?,那么圆锥的底面积是4cm?。( )
我爱展示
一个圆柱体和一个圆锥体的体积相等,它们的底面积的比是3:5,圆柱的高8厘米,圆锥的高是( )厘米。
把一个体积是120cm?的圆柱形木材削成一个最大的圆锥,则削去部分的体积是( )cm?
(2010年广州市大联盟小升初试题)一个圆柱体和一个圆锥体等底等高,他们的体积和是72立方分米,圆锥的体积是
( )立方分米,圆柱体的体积是( )立方分米。4. 等底等高的正方体、长方体的和圆柱的体积都相等( )
圆柱体的体积与圆锥体的体积比是3:1。( )
等体积等高的圆柱和圆锥:圆柱的底面积是圆锥的底面积的3倍。( )
692063193701计算下列圆柱的体积。
2699401-166506(1) (2)
一个圆柱形鱼缸,底面直径是40cm,高是25cm,里面盛了一些水,把一个底面半径为10cm的圆锥放入鱼缸中(圆锥全 部浸入水中),鱼缸中的水面升高了2cm。这个圆锥的高是多少?
2532894266735
限时考场模拟
1.
等底等高的圆柱和圆锥,圆柱的体积是圆锥的(
),圆锥的体积是圆柱的(
),圆柱的体积比圆锥大
(
),圆锥的体积比圆柱小( )。
一个圆柱和一个圆锥的体积都是24.6立方分米,底面积都是6平方分米,那么圆柱的高是( )分米,圆锥的高是( )分米。
(2014年天河区小升初数学招生试卷).一个圆柱与一个圆锥体积相等,底面积也相等。已知圆柱的高是12cm,圆锥 的高是( )cm。
课后作业
(2012年大联盟小升初试题)一个圆锥与一个圆柱的底面积相等,已知圆锥与圆柱的体积比是1:9,圆锥的高是4.8 厘米,则圆柱的高是( )厘米。
一个圆锥的体积是10.8立方米,与它等底等高的圆柱的体积是( )。
一个圆锥的体积是50.24立方米,底面半径是2米,它的高是( )米。
一个圆柱的底面半径是3分米,高2分米,体积是( )立方分米
一个圆锥体,底面直径和高都是3cm,它的体积是( )立方厘米
一个圆锥的体积是75.36dm?,底面半径是3dm,它的高是( )dm
V=Sh只能求圆柱的体积( )
圆柱和圆锥都有无数条高。( )
一个圆锥的底面半径扩大到原来的5倍,它的体积也扩大到原来的25倍。( )
[单选题] 同底等高的圆柱体的体积是圆锥体积的( )
A.3倍 B. C.无法确定
11. [单选题]
将一个圆柱体铝块熔铸成圆锥体,它的(
)不变。
A.表面积
B.体积
C.底面积
12. [单选题] 一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的( )被。
A.2 B.4 C.6
13.
[单选题]
一个圆锥的体积是3m?,底面积是3㎡,它的高是(
)m。
A.3
B.1
C.
5123008434202
[单选题] (2013年广州市小联盟数学试题)把底面积是18平方厘米,高是2厘米的圆柱形零件削成最大的圆锥体, 削成的最大圆锥体的体积是( )立方厘米
A.12 B.18 C.24 D.36
70131445955419485313366964022210246792计算下图的体积。(单位:cm)
(1) (2) (3)
一个圆柱体和一个圆锥体等底等高,它们的体积相差50.24立方厘米。如果圆锥体的底面半径是2厘米,这个圆锥体 的高是多少厘米?
一个圆锥形沙堆,它的底面周长是12.56m,高是1.8m。用这堆沙子在8m宽的公路上铺3cm厚的路面,能铺多少米?
有一囤稻谷,上面是圆锥形,下面是圆柱,量得圆柱的底面周长是6.28米,高是2米,圆锥的高0.3米,这囤稻谷重 多少千克?(每立方米稻谷重650千克)
(2014年广州市小联盟数学试题)唐老鸭用一个圆锥形容器装满了2000克香油,米老鼠趁唐老鸭不在,在容器的中 间咬了一个洞,然后开始偷油,一直偷到油面与小洞平齐为止(如图)。问:米老鼠共偷得香油多少克(容器的厚度不 计)?
2532894112798
1、学完这节课的内容后,回去复习圆锥和圆柱的知识。
2、标注理解不够深刻的例题及时复习整理。
3、总结圆柱与圆锥的体积应用题。
4、整理课堂上做错的习题到错题本上,课下及时完成相应练习。
2532894211904
课首小测
1.39千克。
解析:5米=500厘米
40÷4×500×7.8=39000(克)
=39(千克) 答:这段钢材重39千克。
2.1413cm?。
解析:3.14×5?×18
=3.14×25×18
=1413(cm?)
答:它的体积是1413 cm?。
导学一
知识点讲解 1:圆锥的认识例题
圆;曲面;扇形
顶点;圆心;垂直距离
我爱展示
5012262619501.1
2.
知识点讲解 2:圆锥的体积
例题
1.4cm
解析: ×12=4(cm)
答:这时乙容器中的水有4cm。2.4分米
解析: ×3.14×2?×3÷(1?×3.14)=4(分米)
答:圆柱形容器的水深4分米。3.26.17dm?
解析: ×[3.14×(5÷2)?]×4≈26.17(dm?)
答:圆锥的体积约为26.17 dm?。
我爱展示
1.A
解析: 圆锥的体积=底面积×高× ,当底面积扩大3倍时,
圆锥现在的体积=(底面积×3)×高× ,即3倍圆锥原来的体积。所以选扩大到原来的3倍。2.(1)25.12dm?;(2)188.4cm?;(3)1.57m?
解析:(1) ×3.14×(4÷2)?×6=25.12(dm?)
(2)2dm=20cm ×3.14×3?×20=188.4(cm?)
(3) ×3.14×(6.28÷3.14÷2)?×1.5=1.57(m?)
导学二
知识点讲解 1:已知圆锥的底面积和高,求圆锥的体积。例题
1.64cm?。
解析: ×24×8=64(cm?)
答:这个铁锤的体积是64cm?
知识点讲解 2:已知圆锥的底面半径和高,求圆锥的体积。例题
1.113.04cm?。
解析: 3.14×3?=28.26(cm?) ×28.26×12=113.04(cm?)
答:这个圆锤的体积是113.04cm?
知识点讲解 3:已知圆锥的底面直径和高,求圆锥的体积。例题
1.5.02m?;7.53t。
解析:(1)沙堆的底面积:3.14×(4÷2)?
=3.14×4
=12.56(m?)
(2)沙堆的体积: ×12.56×1.2
=12.56×0.4
=5.024(m?)
≈5.02(m?)
(3)沙堆的质量:5.02×1.5=7.53(t)
答:这堆沙子的体积大约是5.03m?,大约重7.53t。
知识点讲解 4:已知圆锥的底面周长和高,求圆锥的体积。例题
1.56.52m?。
解析: 圆锥的底面积:3.14×(18.84÷3.14÷2)?
=3.14×9
=28.26(m?)
圆锥的体积: ×28.26×6
=2×28.26
=56.52(m?)。答:塔的顶端的体积是56.52m?
我爱展示
1.4710千克
解析: ×3.14×(12.56÷3.14÷2)? ×1.5×750=4710(kg)
答:这堆小麦重4710千克。
2.23个
解析:3.14×(9.42÷3.14÷2)?×1.2× ×730÷90≈23(个)
答:需要23个袋子。3.7.5平方厘米
解析: 0.05×(5×60)÷ ÷6=7.5(cm?)
答:这个沙漏的底面积是7.5平方厘米。
导学三
知识点讲解 1:等底等高的圆柱和圆锥:圆锥的体积等于和它等底等高的圆柱体积的。例题
1.18.84。
解析: 因为圆锥的体积等于和它等底等高的圆柱体积的 ,所以圆锥的体积= ×圆柱的体积即 ×3.14×3?×2=18.84(cm?)
知识点讲解 2:等底等体积的圆柱和圆锥:圆锥的高是圆柱的高的3倍,或者说圆锥的高比圆柱的高多2倍;圆柱的高是圆锥的高的 ,或者说圆柱的高比圆锥的高少 。
例题
1.对
解析:因为等底等体积的圆柱和圆锥,圆锥的高是圆柱的高的3倍;圆柱的高是3cm,圆锥的高是9cm;故此题判断对。
知识点讲解 3: 例题
1.错
266240090620380020090620544677290620627930944370解析:因为等高等体积的圆柱和圆锥中, , ;根据公式 , ,
得:
244039135464圆柱的底面积×圆柱的高= 圆锥的底面积×圆锥的高 → 3倍圆柱的底面积=圆锥的底面积 → 圆锥的底面积
=3×12=36(cm?)。
我爱展示
1.14.4厘米
110833290699470673990699解析: 已知 ,圆柱与圆锥的底面积之比是3:5;根据公式 , ,得:
95107573916→
=14.4(厘米)。
→
圆锥的高= 2.80
解析: 把一个圆柱削成一个最大的圆锥,这个圆锥与圆柱等底等高,所以
削去部分的体积=圆柱的体积-圆锥的体积
且等底等高的圆锥的体积等于圆柱体积的 即削去部分的体积=120- ×120=80(cm?)
3.18;54
解析: 等底等高的圆柱和圆锥的体积比: 所以圆锥的体积:72÷(1+3)=18(立方分米)
圆柱的体积:72-18=54(立方分米)
对
错
解析:等底等高的圆柱和圆锥的体积比: ,故判断为错6.错
解析:等体积等高的圆柱和圆锥:圆柱的底面积是圆锥的底面积的 倍。故判断为错。7.(1)1130.4cm?;(2)251.2cm?
解析:(1)3.14×6?×10=1130.4(cm?);(2)3.14×( )?×20=251.2(cm?) 8.24cm
解析: 3.14×(40÷2)?×2×3÷(3.14×10?)
=7536÷314
=24(cm)
答:这个圆锥的高是24cm。
限时考场模拟
1.3倍; ;2倍;
2.4.1;12.3
解析: 圆锥的体积= ×底面积×高;圆锥的高=圆锥的体积×3÷底面积, 所以圆锥的高是:24.6×3÷6=12.3(分米)
圆柱的体积=底面积×高;圆柱的高=圆柱的体积÷底面积, 即 圆柱的高是:24.6÷6=4.1(分米)
3.36
解析: 本题主要考察了圆柱和圆锥等体等底的情况下,它们的高的关系的知识点。圆柱和圆锥等体等底的情况下,圆锥的高是圆柱高的3倍,所以12×3=36。
课后作业
1.14.4
110833290699438297590699解析: 已知 ,圆柱与圆锥的底面积相等;根据公式 , ,得:
95107564676388345464676→ →
圆柱的高=3×4.8=14.4(厘米)。2.32.4立方米
解析: 等底等高的圆柱和圆锥,圆柱的体积是圆锥的体积的3倍
即 圆柱的体积=圆锥的体积×3=10.8×3=32.4(立方米)
3.12
解析: 圆锥的体积=底面积×高,圆锥的高=圆锥的体积÷ ÷底面积即 圆锥的高:50.24÷ ÷(3.14×2?)=12(米)
4.56.52
解析:3.14×3?×2=56.52(立方分米) 5.7.065
解析: ×3.14×(3÷2)?×3=7.065(立方厘米)
6.8
解析:75.36÷ ÷(3.14×3?)=8(dm) 7.错
解析:不只是圆柱的体积=底面积×高8.错
解析:圆柱有无数条高,但是圆锥只有一条高。9.对
解析:圆锥的体积= ×底面积×高,底面半径扩大5倍,底面半径就扩大25倍,圆锥的体积也扩大25倍,故判断为√。
10.A
解析: 因为圆锥的体积= ×底面积×高,圆柱的体积=底面积×高,所以同底等高的圆柱体的体积是圆锥体的3倍。11.B
12.B
13.A
解析: 圆锥的体积= ×底面积×高,高=圆锥的体积÷ ÷底面积=3÷ ÷3=3(m) 14.A
解析:圆锥的体积: ×18×2=12(立方厘米) 15.(1)25.12cm?;(2)10.99cm?;(3)9.57cm? 解析:(1) ×3.14×2?×6=25.12(cm?);
(2)3.14×(2÷2)?×4- ×3.14×(2÷2)?×1.5=10.99(cm?);
(3)2×2×2+3.14×(1÷2)?×2=9.57(cm?) 16.6厘米
解析:等底等高的圆柱和圆锥体,圆柱的体积比圆锥的体积多2倍。圆锥的体积:50.24÷2=25.12(立方厘米)
圆锥体的高:25.12×3÷(3.14×2?)
=75.36÷12.56
=6(厘米) 答:这个圆锥体的高是6厘米。
17.31.4米
解析:3cm=0.03m ×3.14×(12.56÷3.14÷2)?×1.8÷(8×0.03)=31.4(米)
答:能铺31.4米。18.4286.1千克
解析:稻谷的体积: ×3.14×(6.28÷3.14÷2)?×0.3+3.14×(6.28÷3.14÷2)?×2=6.594(立方米)
稻谷的重量:6.594×650=4286.1(千克) 答:这囤稻谷重4286.1千克。
19.1750克
解析: 剩下的油和原来的油的体积相似,现在油的高度和原来油的高度比是1:2,那么它们的体积比是1:8,
即剩下的油的体积是原来的油的体积的 。米老鼠偷走了1- = ,2000× =1750(克) 答:米老鼠共偷得香油1750克。
