人教版八年级上册数学课件:11.3.2多边形的内角和(18张)
文档属性
| 名称 | 人教版八年级上册数学课件:11.3.2多边形的内角和(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 08:48:53 | ||
图片预览



文档简介
(共18张PPT)
11.3.2多边形的内角和与外角和
第十一章
三角形
一、知识回顾
1、多边形的定义:
2、从多边形的一个顶点出发能画几条对角线?把
多边形分成几个三角形?
3、多边形的对角线:
4、正多边形:
B
A
C
D
E
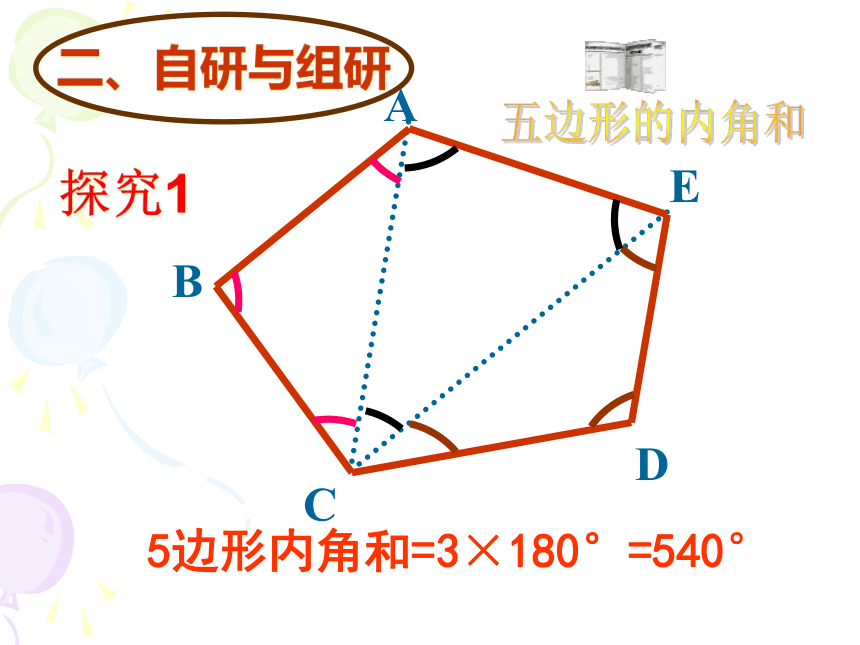
探究1
5边形内角和=3×180°=540°
二、自研与组研
五边形的内角和
三角形的内角和是
度;
四边形可分成
个三角形,其内角和是
度;
五边形可分成
个三角形,其内角和是
度;
六边形可分成
个三角形,其内角和是
度;
…
…
十五边形可分成
个三角形,其内角和是
度;
…
…
n边形可分成
个三角形,其内角和是
度。
180
2
360
3
540
4
720
13
2340
(n-2)
(n-2)
·180
探究2
多边形的内角和
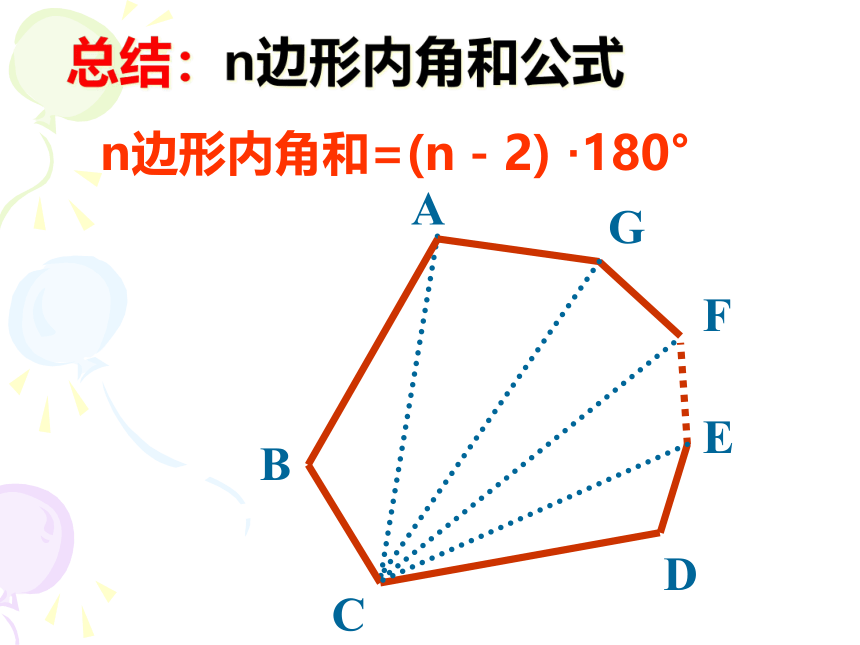
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2)
·180°
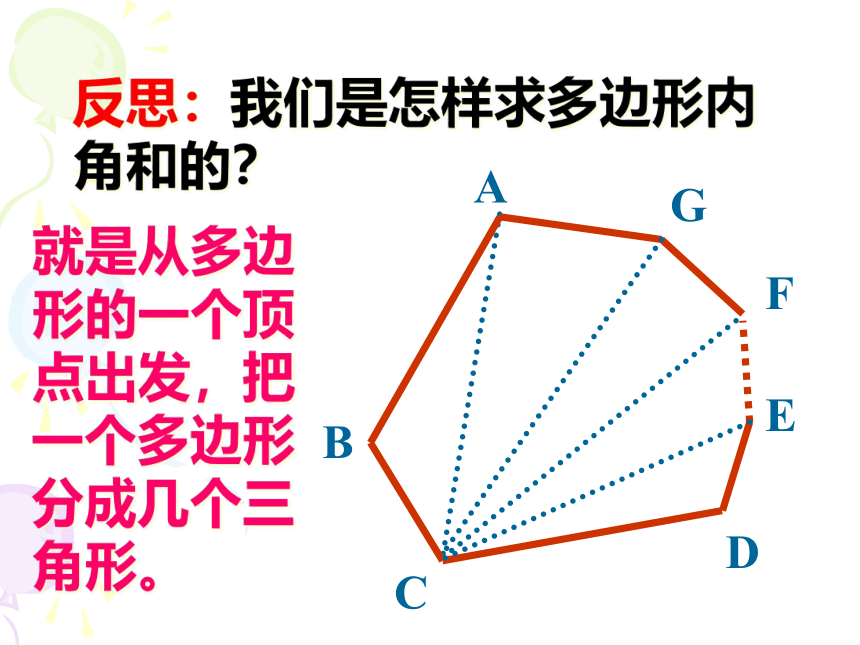
反思:我们是怎样求多边形内
角和的?
B
A
C
D
G
F
E
就是从多边形的一个顶点出发,把一个多边形分成几个三角形。
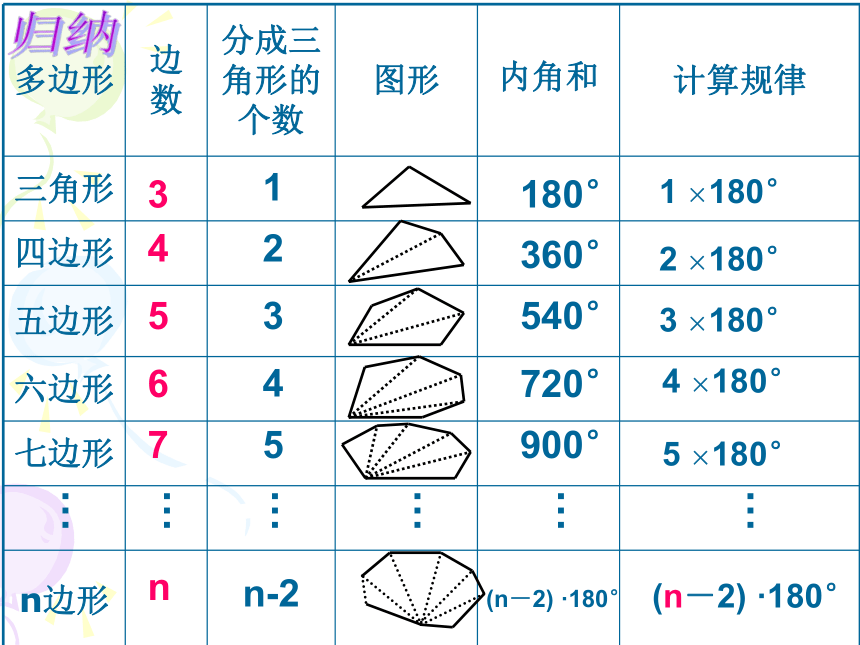
多边形
边数
分成三角形的个数
图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2)
·180°
(n-2)
·180°
5
×180°
4
×180°
3
×180°
2
×180°
1
×180°
归纳
十二边形的内角和是(
)。
一个多边形当边数增加1时,它的内角和增加(
)。
一个多边形的内角和是720?,则此多边形共有(
)个内角。
如果一个多边形的内角和是1440度,那么这是(
)边形。
1800?
180?
六
十
三、走进展研
5、如果一个多边形的内角和是1440度,那么这是
边形。
解:由多边形的内角和公式可得
(n
-
2)·
180
=
1440
(n
-
2)
=
8
n
=
10
∴这是十边形。
十
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
结论:五边形的外角和等于360°
-(5-2)
×
180°
=360
°
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2)
×
180°
=360
°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180
°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360?
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
n边形外角和=360
°
四、走进升研
2、正五边形的每一个外角等于____,每一个内角等于_____。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108
°
3、
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:
设多边形的边数为n
则
(n-2)?180°=360°×
2,
解得:
n=6
∴这个多边形的边数为6。
想想这节课你有哪些收获?
看看谁最棒?
11.3.2多边形的内角和与外角和
第十一章
三角形
一、知识回顾
1、多边形的定义:
2、从多边形的一个顶点出发能画几条对角线?把
多边形分成几个三角形?
3、多边形的对角线:
4、正多边形:
B
A
C
D
E
探究1
5边形内角和=3×180°=540°
二、自研与组研
五边形的内角和
三角形的内角和是
度;
四边形可分成
个三角形,其内角和是
度;
五边形可分成
个三角形,其内角和是
度;
六边形可分成
个三角形,其内角和是
度;
…
…
十五边形可分成
个三角形,其内角和是
度;
…
…
n边形可分成
个三角形,其内角和是
度。
180
2
360
3
540
4
720
13
2340
(n-2)
(n-2)
·180
探究2
多边形的内角和
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2)
·180°
反思:我们是怎样求多边形内
角和的?
B
A
C
D
G
F
E
就是从多边形的一个顶点出发,把一个多边形分成几个三角形。
多边形
边数
分成三角形的个数
图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2)
·180°
(n-2)
·180°
5
×180°
4
×180°
3
×180°
2
×180°
1
×180°
归纳
十二边形的内角和是(
)。
一个多边形当边数增加1时,它的内角和增加(
)。
一个多边形的内角和是720?,则此多边形共有(
)个内角。
如果一个多边形的内角和是1440度,那么这是(
)边形。
1800?
180?
六
十
三、走进展研
5、如果一个多边形的内角和是1440度,那么这是
边形。
解:由多边形的内角和公式可得
(n
-
2)·
180
=
1440
(n
-
2)
=
8
n
=
10
∴这是十边形。
十
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
结论:五边形的外角和等于360°
-(5-2)
×
180°
=360
°
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2)
×
180°
=360
°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180
°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360?
1、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
n边形外角和=360
°
四、走进升研
2、正五边形的每一个外角等于____,每一个内角等于_____。
5X=360°
X=72°
72°
108°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108
°
3、
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:
设多边形的边数为n
则
(n-2)?180°=360°×
2,
解得:
n=6
∴这个多边形的边数为6。
想想这节课你有哪些收获?
看看谁最棒?
