2020年北师大版八年级数学上册第三章位置与坐标国庆自测作业(word版,含答案)
文档属性
| 名称 | 2020年北师大版八年级数学上册第三章位置与坐标国庆自测作业(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 152.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 00:00:00 | ||
图片预览



文档简介
北师大版八年级数学上册
第三章位置与坐标
国庆自测作业
一.选择题
1.在平面直角坐标系中,已知点P(2,-3),则点P在
( )
A.第一象限 B.第二象限
C.第三象限
D.第四象限
2.在平面直角坐标系中,点A(-3,0)在( )
A.x轴正半轴上
B.x轴负半轴上
C.y轴正半轴上
D.y轴负半轴上
3.已知点A(m+1,﹣2)和点B(3,m﹣1),若直线AB∥x轴,则m的值为(
)
A.2
B.﹣4
C.﹣1
D.3
4.在平面直角坐标系中,若点P在轴上,则的值是(?
)
A.-3
B.1
C.3
D.-1
5.设点A(m,n)在x轴上,且位于原点的左侧,则下列结论正确的是
( )
A.m=0,n为一切实数
B.m=0,n<0
C.m为一切实数,n=0
D.m<0,n=0
6.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为( ).
A.(-4,0)
B.(6,0)
C.(-4,0)或(6,0)
D.无法确定
7.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是( )
A.(3,1)
B.(﹣3,﹣1)
C.(1,﹣3)
D.(3,﹣1)
8.若0<a<1,则点M(a﹣1,a)在第(?)象限.
A.一
B.二
C.三
D.四
9.如果点A(m,n)在第二象限,那么点B(-m,|n|)在
( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10.如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到长方形OABC的边时反弹,反弹时反射角等于入射角.小球第1次碰到长方形的边时的点为P1,第2次碰到长方形的边时的点为P2……第n次碰到长方形的边时的点为Pn,则点P3的坐标是(8,3),点P2
018的坐标是( )
A.(8,3)
B.(7,4)
C.(5,0)
D.(3,0)
二.填空题
11.(5分)如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,﹣1)和(﹣3,1),那么“卒”的坐标为
.
在电影票上,将“7排6号”表示为(7,6),那么“5排4号”应该表示
为___________.
13.一只蚂蚁由点(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是 .?
14.点__________与(-3,7)关于x轴对称,点__________与(-3,7)关于y轴对称,点(-3,7)与(-3,-2)之间的距离是________.
15.当x=
时,点M(x﹣3,x﹣1)在y轴上.
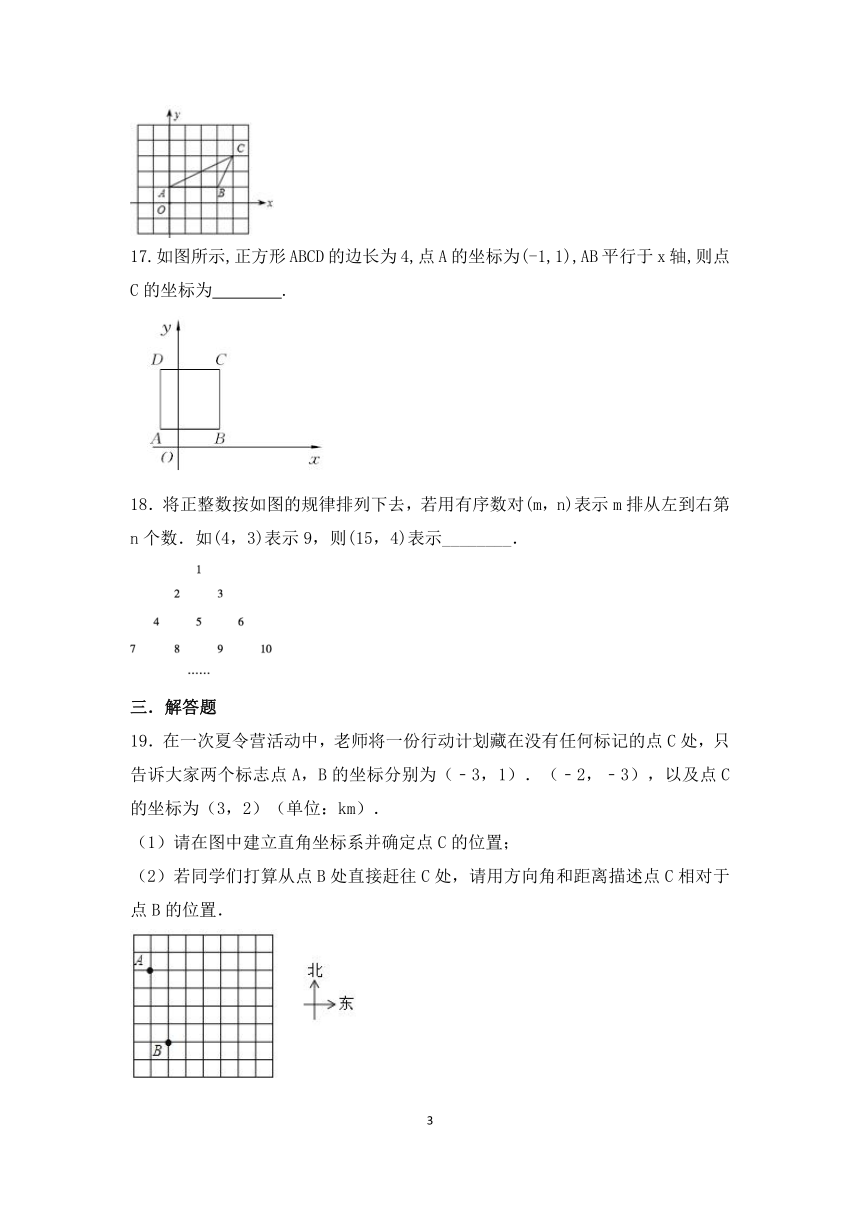
16.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3)如果要使以点A.B.D为顶点的三角形与△ABC全等,那么点D的坐标是_____________.
17.如图所示,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为 .
?
18.将正整数按如图的规律排列下去,若用有序数对(m,n)表示m排从左到右第n个数.如(4,3)表示9,则(15,4)表示________.
三.解答题
19.在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(﹣3,1).(﹣2,﹣3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立直角坐标系并确定点C的位置;
(2)若同学们打算从点B处直接赶往C处,请用方向角和距离描述点C相对于点B的位置.
20.如图所示,在直角坐标系中,RtΔAOB的两条直角边OA,OB分别在x轴的负半轴和y轴的负半轴上,且OA=2,OB=1.将RtΔAOB绕点O按顺时针方向旋转90°,再把所得的三角形沿x轴正方向平移1个单位长度,得ΔCDO.
(1)写出点A,C的坐标;
(2)求点A和点C之间的距离.
21.在直角坐标系中,有点A(3,0),B(0,4),若有一个直角三角形与Rt△ABO全等且它们只有一条公共直角边,请写出这些直角三角形各顶点的坐标(不要求写计算过程).
22.在平面直角坐标系xOy中,点M的坐标为(3,﹣2),线段AB的位置如图所示,其中点A的坐标为(7,3),点B的坐标为(1,4).
(1)将线段AB平移可以得到线段MN,其中点A的对应点为M(3,﹣2),点B的对应点为N,则点N的坐标为
.
(2)在(1)的条件下,若点C的坐标为(4,0),请在图中描出点N并顺次连接BC,CM,MN,NB,然后求出四边形BCMN的面积S.
23.已知点A(a,3),B(-4,b),试根据下列条件求出a,b的值
(1)A.B两点关于y轴对称;
(2)A.B两点关于原点对称;
(3)A.B两点关于x轴对称;
(4)A.B两点在第二.四象限的角平分线上
24.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一个动点,求PA+PC的最小值是多少?
答案提示
1.D
2.B
3.C.4.B.
5.D
6.C
7.A.8.B.9.A10.B
11.(﹣2,﹣2).
12.(5,4)
13.(3,2)
14.(-3,-7);(3,7);9
15.3.
16.(4,-1).(-1,3).(-1,-1)
17.(3,5)
18.109
19.解:(1)根据A(﹣3,1),B(﹣2,﹣3)画出直角坐标系,
描出点C(3,2),如图所示;
(2)BC=5,所以点C在点B北偏东45°方向上,距离点B的5
km处.
20.解:(1)点A的坐标是(-2,0),点C的坐标是(1,2). (2)如图所示,连接AC,在RtΔACD中,AD=OA+OD=3,CD=2,∴AC2=CD2+AD2=22+32=13,∴AC=.
21.解:根据两个三角形全等及有一条公共直角边,可利用轴对称得到满足这些条件的直角三角形共有6个.如图:
①Rt△OO1A,②Rt△OBO1,③Rt△A2BO,④Rt△A1BO,⑤Rt△OB1A,⑥Rt△OAB2.
这些三角形各个顶点的坐标分别为:①(0,0),(3,4),(3,0);
②(0,0),(0,4),(3,4);
③(-3,4),(0,4),(0,0);
④(-3,0),(0,4),(0,0);
⑤(0,0),(0,-4),(3,0);
⑥(0,0),(3,0),(3,-4).
22.解:(1)由点M(3,﹣2)的对应点A(7,3)知先向右平移4个单位.再向上平移5个单位,
∴点B(1,4)的对应点N的坐标为(﹣3,﹣1),
故答案为:(﹣3,﹣1).
(2)如图,描出点N并画出四边形BCMN,
S=×4×5+×6×1+×1×2+2×1+×3×4
=10+3+1+2+6
=22.
23.解:(1)A.B两点关于y轴对称,
故有a=4,b=3;
(2)A.B两点关于原点对称,
故有a=4,b=-3
(3)A.B两点关于x轴对称;
所以有a=-4,b=-3;
(4)如图:
根据题意,a+3=0;
b-4=0;
所以a=-3,b=4.
24.解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,
则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(3,),
∴AB=,OA=3,∠B=60°,由勾股定理得:OB=,
由三角形面积公式得:×OA×AB=×OB×AM,
∴AM=,
∴AD=2×=3,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN=AD=,由勾股定理得:DN=,
∵C(,0),
∴CN=3--=1,
在Rt△DNC中,由勾股定理得:DC=,
即PA+PC的最小值是,
第三章位置与坐标
国庆自测作业
一.选择题
1.在平面直角坐标系中,已知点P(2,-3),则点P在
( )
A.第一象限 B.第二象限
C.第三象限
D.第四象限
2.在平面直角坐标系中,点A(-3,0)在( )
A.x轴正半轴上
B.x轴负半轴上
C.y轴正半轴上
D.y轴负半轴上
3.已知点A(m+1,﹣2)和点B(3,m﹣1),若直线AB∥x轴,则m的值为(
)
A.2
B.﹣4
C.﹣1
D.3
4.在平面直角坐标系中,若点P在轴上,则的值是(?
)
A.-3
B.1
C.3
D.-1
5.设点A(m,n)在x轴上,且位于原点的左侧,则下列结论正确的是
( )
A.m=0,n为一切实数
B.m=0,n<0
C.m为一切实数,n=0
D.m<0,n=0
6.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为( ).
A.(-4,0)
B.(6,0)
C.(-4,0)或(6,0)
D.无法确定
7.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(﹣1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是( )
A.(3,1)
B.(﹣3,﹣1)
C.(1,﹣3)
D.(3,﹣1)
8.若0<a<1,则点M(a﹣1,a)在第(?)象限.
A.一
B.二
C.三
D.四
9.如果点A(m,n)在第二象限,那么点B(-m,|n|)在
( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10.如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到长方形OABC的边时反弹,反弹时反射角等于入射角.小球第1次碰到长方形的边时的点为P1,第2次碰到长方形的边时的点为P2……第n次碰到长方形的边时的点为Pn,则点P3的坐标是(8,3),点P2
018的坐标是( )
A.(8,3)
B.(7,4)
C.(5,0)
D.(3,0)
二.填空题
11.(5分)如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,﹣1)和(﹣3,1),那么“卒”的坐标为
.
在电影票上,将“7排6号”表示为(7,6),那么“5排4号”应该表示
为___________.
13.一只蚂蚁由点(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是 .?
14.点__________与(-3,7)关于x轴对称,点__________与(-3,7)关于y轴对称,点(-3,7)与(-3,-2)之间的距离是________.
15.当x=
时,点M(x﹣3,x﹣1)在y轴上.
16.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3)如果要使以点A.B.D为顶点的三角形与△ABC全等,那么点D的坐标是_____________.
17.如图所示,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为 .
?
18.将正整数按如图的规律排列下去,若用有序数对(m,n)表示m排从左到右第n个数.如(4,3)表示9,则(15,4)表示________.
三.解答题
19.在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(﹣3,1).(﹣2,﹣3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立直角坐标系并确定点C的位置;
(2)若同学们打算从点B处直接赶往C处,请用方向角和距离描述点C相对于点B的位置.
20.如图所示,在直角坐标系中,RtΔAOB的两条直角边OA,OB分别在x轴的负半轴和y轴的负半轴上,且OA=2,OB=1.将RtΔAOB绕点O按顺时针方向旋转90°,再把所得的三角形沿x轴正方向平移1个单位长度,得ΔCDO.
(1)写出点A,C的坐标;
(2)求点A和点C之间的距离.
21.在直角坐标系中,有点A(3,0),B(0,4),若有一个直角三角形与Rt△ABO全等且它们只有一条公共直角边,请写出这些直角三角形各顶点的坐标(不要求写计算过程).
22.在平面直角坐标系xOy中,点M的坐标为(3,﹣2),线段AB的位置如图所示,其中点A的坐标为(7,3),点B的坐标为(1,4).
(1)将线段AB平移可以得到线段MN,其中点A的对应点为M(3,﹣2),点B的对应点为N,则点N的坐标为
.
(2)在(1)的条件下,若点C的坐标为(4,0),请在图中描出点N并顺次连接BC,CM,MN,NB,然后求出四边形BCMN的面积S.
23.已知点A(a,3),B(-4,b),试根据下列条件求出a,b的值
(1)A.B两点关于y轴对称;
(2)A.B两点关于原点对称;
(3)A.B两点关于x轴对称;
(4)A.B两点在第二.四象限的角平分线上
24.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一个动点,求PA+PC的最小值是多少?
答案提示
1.D
2.B
3.C.4.B.
5.D
6.C
7.A.8.B.9.A10.B
11.(﹣2,﹣2).
12.(5,4)
13.(3,2)
14.(-3,-7);(3,7);9
15.3.
16.(4,-1).(-1,3).(-1,-1)
17.(3,5)
18.109
19.解:(1)根据A(﹣3,1),B(﹣2,﹣3)画出直角坐标系,
描出点C(3,2),如图所示;
(2)BC=5,所以点C在点B北偏东45°方向上,距离点B的5
km处.
20.解:(1)点A的坐标是(-2,0),点C的坐标是(1,2). (2)如图所示,连接AC,在RtΔACD中,AD=OA+OD=3,CD=2,∴AC2=CD2+AD2=22+32=13,∴AC=.
21.解:根据两个三角形全等及有一条公共直角边,可利用轴对称得到满足这些条件的直角三角形共有6个.如图:
①Rt△OO1A,②Rt△OBO1,③Rt△A2BO,④Rt△A1BO,⑤Rt△OB1A,⑥Rt△OAB2.
这些三角形各个顶点的坐标分别为:①(0,0),(3,4),(3,0);
②(0,0),(0,4),(3,4);
③(-3,4),(0,4),(0,0);
④(-3,0),(0,4),(0,0);
⑤(0,0),(0,-4),(3,0);
⑥(0,0),(3,0),(3,-4).
22.解:(1)由点M(3,﹣2)的对应点A(7,3)知先向右平移4个单位.再向上平移5个单位,
∴点B(1,4)的对应点N的坐标为(﹣3,﹣1),
故答案为:(﹣3,﹣1).
(2)如图,描出点N并画出四边形BCMN,
S=×4×5+×6×1+×1×2+2×1+×3×4
=10+3+1+2+6
=22.
23.解:(1)A.B两点关于y轴对称,
故有a=4,b=3;
(2)A.B两点关于原点对称,
故有a=4,b=-3
(3)A.B两点关于x轴对称;
所以有a=-4,b=-3;
(4)如图:
根据题意,a+3=0;
b-4=0;
所以a=-3,b=4.
24.解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,
则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(3,),
∴AB=,OA=3,∠B=60°,由勾股定理得:OB=,
由三角形面积公式得:×OA×AB=×OB×AM,
∴AM=,
∴AD=2×=3,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN=AD=,由勾股定理得:DN=,
∵C(,0),
∴CN=3--=1,
在Rt△DNC中,由勾股定理得:DC=,
即PA+PC的最小值是,
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
