必修1 8. 匀变速直线运动规律的应用课件22张PPT
文档属性
| 名称 | 必修1 8. 匀变速直线运动规律的应用课件22张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 170.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-29 09:18:58 | ||
图片预览








文档简介
匀变速直线运动规律的应用
匀变速直线运动的公式、规律、推论较多,往往一道题多种解法,这就要求同学们在解题时头脑灵活,具有良好的发散思维能力,才能在迅速的找到恰当的方法,可以使解题步骤、运算过程大大简化,起到事半功倍的效?果,
1、基本公式
3、初速度为零的匀加速直线运动的特殊规律
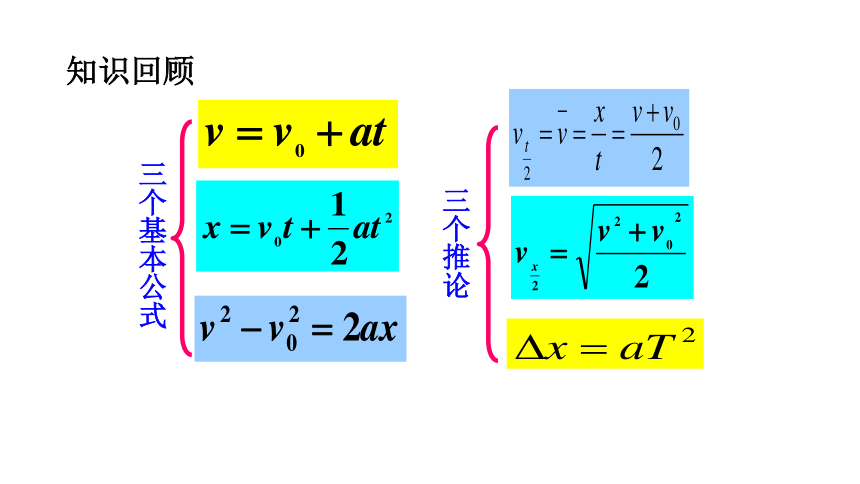
知识回顾
2、推论
知识回顾
三个基本公式
三个推论
初速度为零的匀加速直线运动的特殊规律
三个基本公式
一、等分运动时间
1T末、2T末、3T末……nT末的瞬时速度之比:
1T内、2T内、3T内……nT内的位移之比:
第一个T内、第二个T内……第n个T内的位移之比:
初速度为零的匀加速直线运动的特殊规律
二、等分运动位移
通过1X、2X、3X……所用时间之比:
通过第一个X、第二个X……所用时间之比:
通过1X末、2X末、3X末……的瞬时速度之比:
初速度为零的匀加速直线运动的特殊规律
注意:
1、只适用于初速度为0的匀加速直线运动
2、确定研究的问题(等分运动时间/等分运动位移)
3、区分nT内和第几个T的位移比
nX内和第几个X内的时间比
4、匀减速直线运动可以看做反向的匀加速直线运动
(逆向思维)
经典例题:
一个匀减速直线运动的物体在头两秒内经过的位移是20m,在第二个两秒内经过的位移是12m,求这个物体的加速度和初速度各是多少?
解法1:基本公式法
设初速度为V0,加速度为a,由题意画出草图
由题知:X1=V0t+at2/2
X1+ X2=2V0t+a(2t)2/2
两式联立得:a=-2m/s2 ,V0=12m/s
解法2:基本公式法
设初速度为V0,加速度为a,由题意画出草图
由题知:2aX1= V1 2-V02
2a(X1+ X2)= V2 2-V02
V1= V0+at V2= V0+2at
四式联立得:a=-2m/s2 ,V0=12m/s
解法3:基本公式与推论相结合
设初速度为V0,加速度为a,由题意画出草图
由推论ΔX=aT2得:X2 -X1=at2
X1=V0t+at2/2
联立解得:a=-2m/s2 ,V0=12m/s
根据前边的解答过程,学生得到下列组合:
X2 -X1=at2与 X1+ X2=2V0t+a(2t)2/2
或X2 -X1=at2与2aX1= V12-V02,V1=V0+at
或X2 -X1=at2与2a(X1+ X2)= V22-V02,V2=V0+2at
解法4:基本公式、平均速度与推论相结合
设初速度为V0,加速度为a,由题意画出草图
X2 -X1=at2 ; V1= V0+at
V1=(X1+ X2)/(2t)
联立解得:a=-2m/s2 ,V0=12m/s
或:X2 -X1=at2 ;V1′= V0+at1 V1′= X1/t t1=t/2
或X2 -X1=at2 ;V2′= V0+at2 V2′= X2/t t2=3t/2
解法5:平均速度
设初速度为V0,加速度为a,由题意画出草图
V1′= X1/t;V2′= X2/t;
V1=(X1 +X2)/(2t)
V2′= V1′+at或V2′= V1+at/2或V1= V1′+at/2
得a=-2m/s2
由V1′= V0+at/2 或V1= V0+at或V2′= V0+3at/2
得V0=12m/s
解法6:图像法
设初速度为V0,加速度为a,由题意画出草图
2V1t=X1 +X2
(V1+ V0)t/2= X1
V1= V0+at
联立解得:a=-2m/s2 ,V0=12m/s
解法7:推论与逆向思维
设初速度为V0,加速度为a,由题意画出草图
X2 -X1=at2;X3-X2=at2
解得:a=-2m/s2;X3=4m
X3∶X2 ∶X1=1∶3∶5
所以V3=0;V3= V0+3at
得:V0=12m/s 或2a (X3+X2 +X1)= V02
课堂小结
课堂检测
1、火车紧急刹车后经7s停止,设火车做的是匀减速直线运动,它在最后1s内的位移是2 m,则火车在刹车过程中通过的位移和开始刹车时的速度各是多少?
X=98m
v0=28m/s
D
3、汽车以加速度为2m/s2的加速度由静止开始作匀加速直线运动,求汽车第5秒内的平均速度?
V=9m/s
4、中国女子冰壶队首次夺得世界冠军,如图1-2-7所示,一冰壶以速度v垂直进入三个矩形区域做匀减速运动,且刚要离开第三个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是( )
BD
匀变速直线运动的公式、规律、推论较多,往往一道题多种解法,这就要求同学们在解题时头脑灵活,具有良好的发散思维能力,才能在迅速的找到恰当的方法,可以使解题步骤、运算过程大大简化,起到事半功倍的效?果,
1、基本公式
3、初速度为零的匀加速直线运动的特殊规律
知识回顾
2、推论
知识回顾
三个基本公式
三个推论
初速度为零的匀加速直线运动的特殊规律
三个基本公式
一、等分运动时间
1T末、2T末、3T末……nT末的瞬时速度之比:
1T内、2T内、3T内……nT内的位移之比:
第一个T内、第二个T内……第n个T内的位移之比:
初速度为零的匀加速直线运动的特殊规律
二、等分运动位移
通过1X、2X、3X……所用时间之比:
通过第一个X、第二个X……所用时间之比:
通过1X末、2X末、3X末……的瞬时速度之比:
初速度为零的匀加速直线运动的特殊规律
注意:
1、只适用于初速度为0的匀加速直线运动
2、确定研究的问题(等分运动时间/等分运动位移)
3、区分nT内和第几个T的位移比
nX内和第几个X内的时间比
4、匀减速直线运动可以看做反向的匀加速直线运动
(逆向思维)
经典例题:
一个匀减速直线运动的物体在头两秒内经过的位移是20m,在第二个两秒内经过的位移是12m,求这个物体的加速度和初速度各是多少?
解法1:基本公式法
设初速度为V0,加速度为a,由题意画出草图
由题知:X1=V0t+at2/2
X1+ X2=2V0t+a(2t)2/2
两式联立得:a=-2m/s2 ,V0=12m/s
解法2:基本公式法
设初速度为V0,加速度为a,由题意画出草图
由题知:2aX1= V1 2-V02
2a(X1+ X2)= V2 2-V02
V1= V0+at V2= V0+2at
四式联立得:a=-2m/s2 ,V0=12m/s
解法3:基本公式与推论相结合
设初速度为V0,加速度为a,由题意画出草图
由推论ΔX=aT2得:X2 -X1=at2
X1=V0t+at2/2
联立解得:a=-2m/s2 ,V0=12m/s
根据前边的解答过程,学生得到下列组合:
X2 -X1=at2与 X1+ X2=2V0t+a(2t)2/2
或X2 -X1=at2与2aX1= V12-V02,V1=V0+at
或X2 -X1=at2与2a(X1+ X2)= V22-V02,V2=V0+2at
解法4:基本公式、平均速度与推论相结合
设初速度为V0,加速度为a,由题意画出草图
X2 -X1=at2 ; V1= V0+at
V1=(X1+ X2)/(2t)
联立解得:a=-2m/s2 ,V0=12m/s
或:X2 -X1=at2 ;V1′= V0+at1 V1′= X1/t t1=t/2
或X2 -X1=at2 ;V2′= V0+at2 V2′= X2/t t2=3t/2
解法5:平均速度
设初速度为V0,加速度为a,由题意画出草图
V1′= X1/t;V2′= X2/t;
V1=(X1 +X2)/(2t)
V2′= V1′+at或V2′= V1+at/2或V1= V1′+at/2
得a=-2m/s2
由V1′= V0+at/2 或V1= V0+at或V2′= V0+3at/2
得V0=12m/s
解法6:图像法
设初速度为V0,加速度为a,由题意画出草图
2V1t=X1 +X2
(V1+ V0)t/2= X1
V1= V0+at
联立解得:a=-2m/s2 ,V0=12m/s
解法7:推论与逆向思维
设初速度为V0,加速度为a,由题意画出草图
X2 -X1=at2;X3-X2=at2
解得:a=-2m/s2;X3=4m
X3∶X2 ∶X1=1∶3∶5
所以V3=0;V3= V0+3at
得:V0=12m/s 或2a (X3+X2 +X1)= V02
课堂小结
课堂检测
1、火车紧急刹车后经7s停止,设火车做的是匀减速直线运动,它在最后1s内的位移是2 m,则火车在刹车过程中通过的位移和开始刹车时的速度各是多少?
X=98m
v0=28m/s
D
3、汽车以加速度为2m/s2的加速度由静止开始作匀加速直线运动,求汽车第5秒内的平均速度?
V=9m/s
4、中国女子冰壶队首次夺得世界冠军,如图1-2-7所示,一冰壶以速度v垂直进入三个矩形区域做匀减速运动,且刚要离开第三个矩形区域时速度恰好为零,则冰壶依次进入每个矩形区域时的速度之比和穿过每个矩形区域所用的时间之比分别是( )
BD
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
