六年级上册数学课件-2.4 比例的 基本性质 冀教版 (共22张PPT)
文档属性
| 名称 | 六年级上册数学课件-2.4 比例的 基本性质 冀教版 (共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 679.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 15:46:46 | ||
图片预览



文档简介
根据比例的意义判断下面那两个比可以组成比例。
6∶10 和 9∶15
因为: 6∶10=0.6
9∶15=0.6
0.6=0.6
所以: 6∶10=9∶15
根据比例的意义判断下面那两个比可以组成比例。
20∶5 和 1∶4
因为:20∶5 =4
1∶4 =0.25
4 ≠0.25
所以:20∶5和1∶4
不能组成比例。
6cm
4cm
3cm
2cm
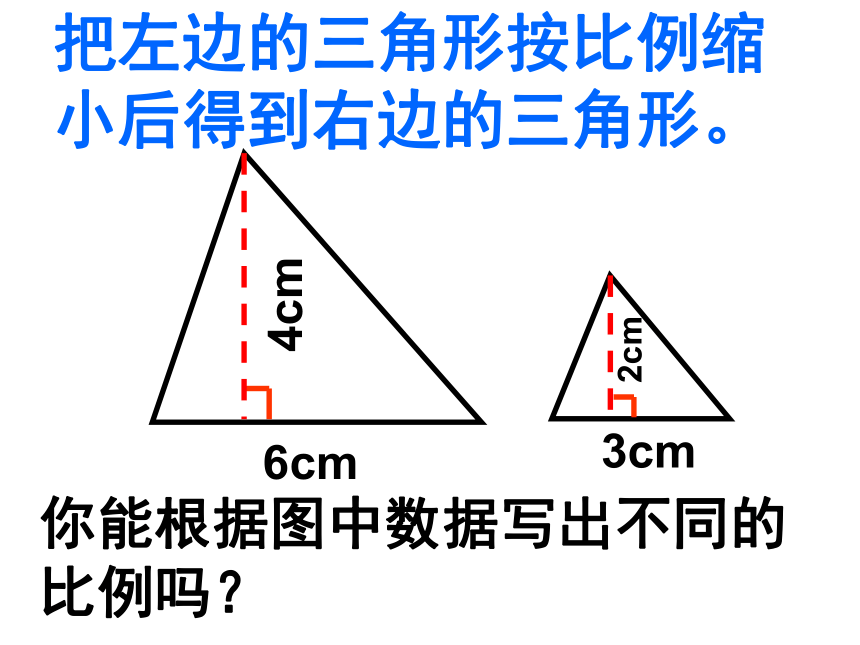
你能根据图中数据写出不同的比例吗?
把左边的三角形按比例缩小后得到右边的三角形。
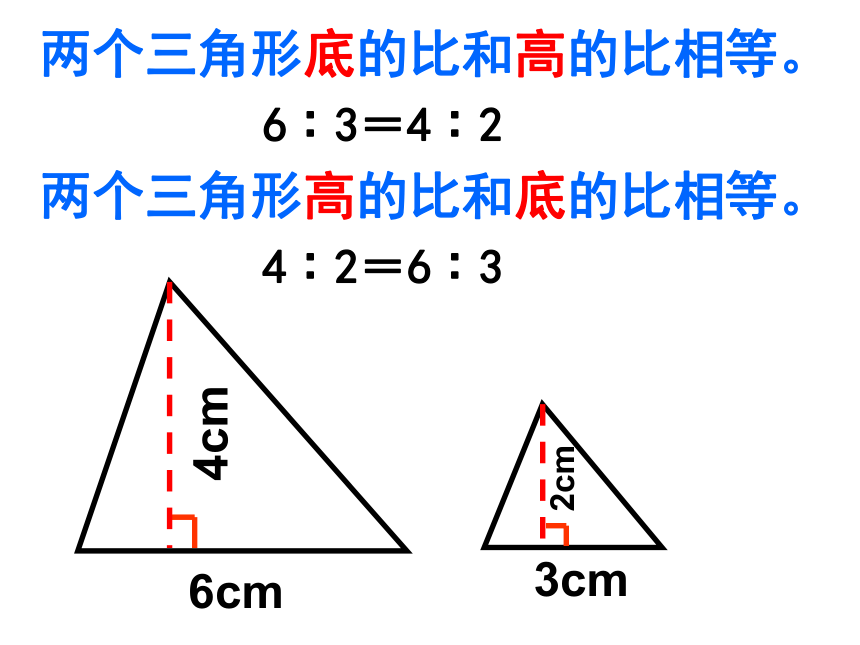
两个三角形底的比和高的比相等。
6∶3=4∶2
两个三角形高的比和底的比相等。
4∶2=6∶3
6cm
4cm
3cm
2cm
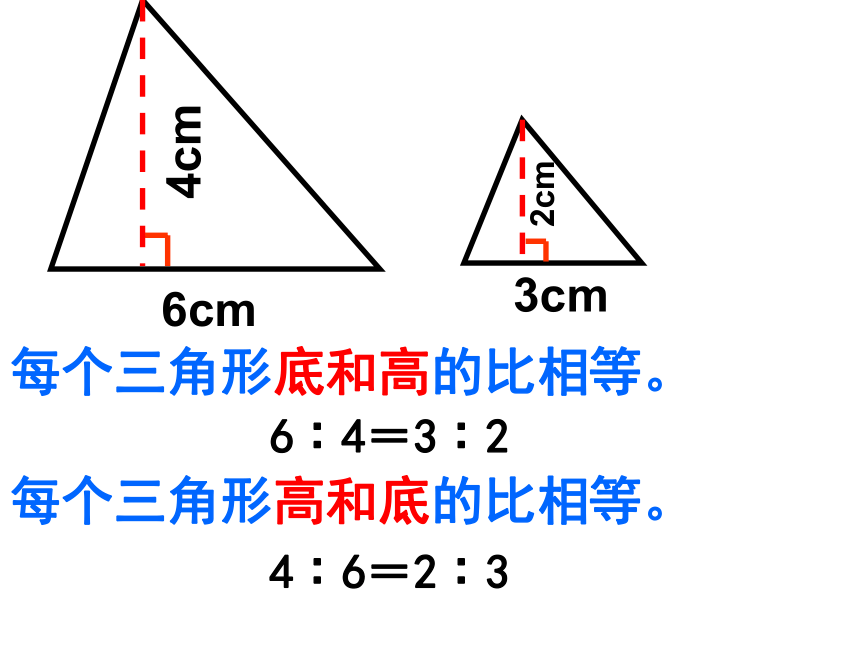
每个三角形底和高的比相等。
6∶4=3∶2
每个三角形高和底的比相等。
4∶6=2∶3
6cm
4cm
3cm
2cm
6 ︰ 3
4 ︰ 2
=
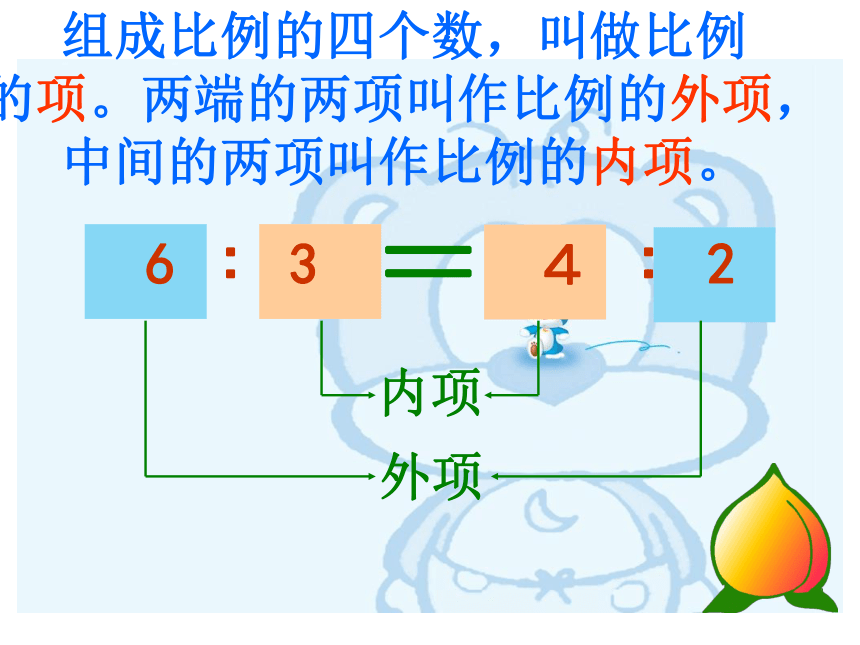
内项
外项
组成比例的四个数,叫做比例
的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。
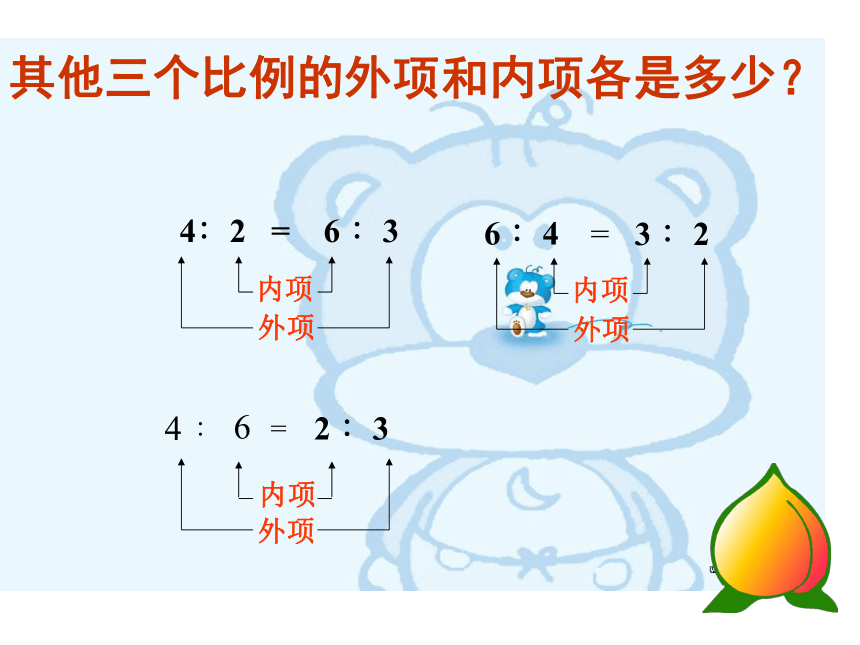
其他三个比例的外项和内项各是多少?
4∶2 = 6 ∶3
6 ∶4
= 3 ∶2
外项
内项
外项
内项
外项
内项
∶
=
2 ∶3
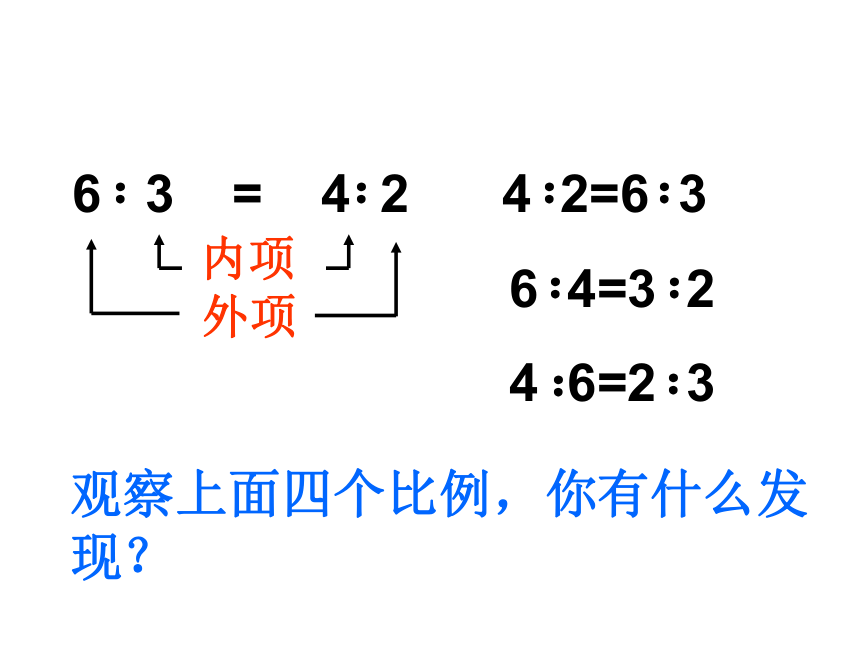
6 3 = 4 2 4 2=6 3
6 4=3 2
4 6=2 3
:
:
:
:
:
:
:
:
内项
外项
观察上面四个比例,你有什么发现?
6 ︰ 3
4 ︰ 2
=
外项
内项
内项积是:
3 × 4=12
外项积是:
6 × 2 =12
6
2
3
4
×
×
=
6 ︰3
4︰2
=
外项
内项
=
6×2
3×4
在比例里,两个外项的积等于两
内项的积。
再写出一些,看看是不是有同样的规律。
5 4=15 12
:
:
0.2 1= 0.6 3
:
:
:
:
1
3
1
4
2
3
1
2
=
如果用字母表示比例的四个项,即a :b=c :d,那么这个规律可以表示成:
a×d=b×c
在比例里,两个内项的积等于两个外项的积,这叫做比例的基本性质。
比 例 的 基 本 性 质
如果把比例写成分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
6×2 =3×4
应用比例的基本性质,判断下面每组
的两个比能否组成比例。如果能组成
比例,把组成的比例写出来。
3.6 :1.8 和 0.5 :0.25
( )×( )=( )
( )×( )=( )
1.8 0.5 0.9
3.6 0.25 0.9
3.6 :1.8 = 0.5 :025
1、应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
9∶12和12∶16
因为: 9 × 16 = 144
12 × 12 = 144
所以: 9∶12 = 12∶16
144 = 144
学校航模小组有男生18人,女生15人;
美术组有男生24人,女生20人。
(1)航模组男、女生人数的比和美术组男、女生人数的比能组成比例吗?
(2)如果能组成比例,指出比例的内项和外项。
18 15=24 20
:
:
4、把图A按比例缩小得到图B,按比例放大得到图C。从图中选择两组数据组成比例,并用比例的基本性质进行检验。
12厘米
9厘米
15厘米
4厘米
3厘米
5厘米
A
B
C
10厘米
8厘米
6厘米
:
:
8 2=24( )
( )
15
=
4
5
5、根据比例的基本性质,在括号里填合适的数。
1.5 3=( )3.4
:
:
48 ( )=3.6 9
:
:
6
12
1.7
120
在一个比例中,两个外项正好互为倒数,已知一个内项是 ,另一个内项是( )
16
3
3
16
思考
下面的四个数可以组成比例吗?把组成的比例写出来(能写几个写几个).
2、3、4 和 6
2 ∶3 = 4 ∶6
2 ∶4 = 3 ∶6
6 ∶3 = 4 ∶2
6 ∶4 = 3 ∶2
4 ∶2 = 6 ∶3
4 ∶6 = 2 ∶3
3 ∶2 = 6 ∶4
3 ∶6 = 2 ∶4
思考
2×6=3×4
最小×最大=中间两数积
比例的基本性质是什么?你觉得学了它有什么用处?
6∶10 和 9∶15
因为: 6∶10=0.6
9∶15=0.6
0.6=0.6
所以: 6∶10=9∶15
根据比例的意义判断下面那两个比可以组成比例。
20∶5 和 1∶4
因为:20∶5 =4
1∶4 =0.25
4 ≠0.25
所以:20∶5和1∶4
不能组成比例。
6cm
4cm
3cm
2cm
你能根据图中数据写出不同的比例吗?
把左边的三角形按比例缩小后得到右边的三角形。
两个三角形底的比和高的比相等。
6∶3=4∶2
两个三角形高的比和底的比相等。
4∶2=6∶3
6cm
4cm
3cm
2cm
每个三角形底和高的比相等。
6∶4=3∶2
每个三角形高和底的比相等。
4∶6=2∶3
6cm
4cm
3cm
2cm
6 ︰ 3
4 ︰ 2
=
内项
外项
组成比例的四个数,叫做比例
的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。
其他三个比例的外项和内项各是多少?
4∶2 = 6 ∶3
6 ∶4
= 3 ∶2
外项
内项
外项
内项
外项
内项
∶
=
2 ∶3
6 3 = 4 2 4 2=6 3
6 4=3 2
4 6=2 3
:
:
:
:
:
:
:
:
内项
外项
观察上面四个比例,你有什么发现?
6 ︰ 3
4 ︰ 2
=
外项
内项
内项积是:
3 × 4=12
外项积是:
6 × 2 =12
6
2
3
4
×
×
=
6 ︰3
4︰2
=
外项
内项
=
6×2
3×4
在比例里,两个外项的积等于两
内项的积。
再写出一些,看看是不是有同样的规律。
5 4=15 12
:
:
0.2 1= 0.6 3
:
:
:
:
1
3
1
4
2
3
1
2
=
如果用字母表示比例的四个项,即a :b=c :d,那么这个规律可以表示成:
a×d=b×c
在比例里,两个内项的积等于两个外项的积,这叫做比例的基本性质。
比 例 的 基 本 性 质
如果把比例写成分数形式,把等号两端的分子、分母交叉相乘,结果怎样?
6×2 =3×4
应用比例的基本性质,判断下面每组
的两个比能否组成比例。如果能组成
比例,把组成的比例写出来。
3.6 :1.8 和 0.5 :0.25
( )×( )=( )
( )×( )=( )
1.8 0.5 0.9
3.6 0.25 0.9
3.6 :1.8 = 0.5 :025
1、应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
9∶12和12∶16
因为: 9 × 16 = 144
12 × 12 = 144
所以: 9∶12 = 12∶16
144 = 144
学校航模小组有男生18人,女生15人;
美术组有男生24人,女生20人。
(1)航模组男、女生人数的比和美术组男、女生人数的比能组成比例吗?
(2)如果能组成比例,指出比例的内项和外项。
18 15=24 20
:
:
4、把图A按比例缩小得到图B,按比例放大得到图C。从图中选择两组数据组成比例,并用比例的基本性质进行检验。
12厘米
9厘米
15厘米
4厘米
3厘米
5厘米
A
B
C
10厘米
8厘米
6厘米
:
:
8 2=24( )
( )
15
=
4
5
5、根据比例的基本性质,在括号里填合适的数。
1.5 3=( )3.4
:
:
48 ( )=3.6 9
:
:
6
12
1.7
120
在一个比例中,两个外项正好互为倒数,已知一个内项是 ,另一个内项是( )
16
3
3
16
思考
下面的四个数可以组成比例吗?把组成的比例写出来(能写几个写几个).
2、3、4 和 6
2 ∶3 = 4 ∶6
2 ∶4 = 3 ∶6
6 ∶3 = 4 ∶2
6 ∶4 = 3 ∶2
4 ∶2 = 6 ∶3
4 ∶6 = 2 ∶3
3 ∶2 = 6 ∶4
3 ∶6 = 2 ∶4
思考
2×6=3×4
最小×最大=中间两数积
比例的基本性质是什么?你觉得学了它有什么用处?
