四年级上册数学课件-4.3 角与角的度量冀教版 (共23张PPT)
文档属性
| 名称 | 四年级上册数学课件-4.3 角与角的度量冀教版 (共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 00:00:00 | ||
图片预览






文档简介
4.3 角与角的度量
本节学习目标:
角的两种定义及角的三种表示方法.
角的度量单位及角的换算.
生活中角的形象!
什么是角呢? 生活中有许多与角有关的实例,观察下图,你能指出图中的角吗?
角是由两条具有公共端点的射线组成的图形。
顶点
射线
射线
边
边
角的定义(静态)
角也可以看做一条射线绕端点旋转所组成的图形。
始边
终边
角的定义(动态)
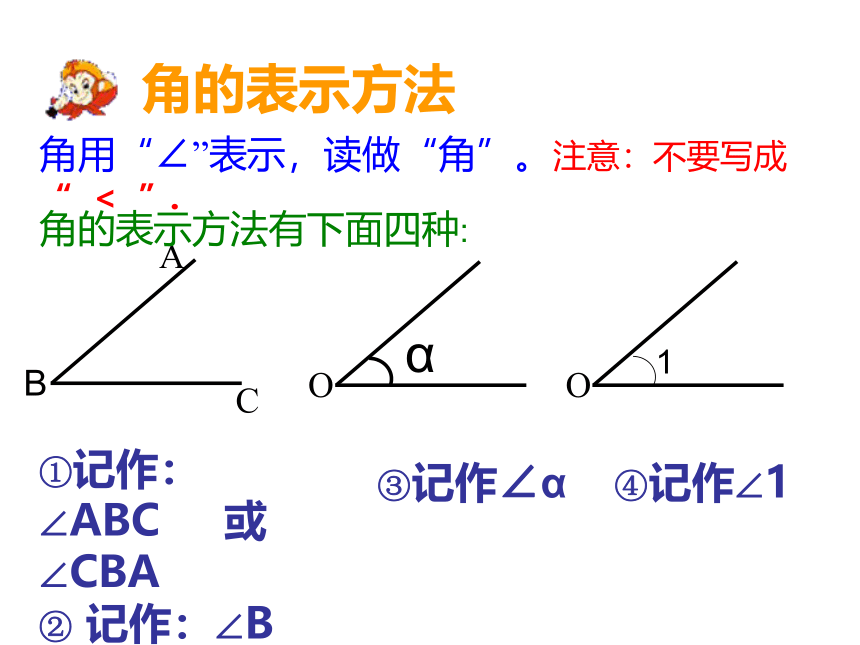
角的表示方法
B
A
C
O
α
O
1
①记作:∠ABC 或∠CBA
② 记作:∠B
③记作∠α
④记作∠1
角用“∠”表示,读做“角”。注意:不要写成“ < ”.
角的表示方法有下面四种:
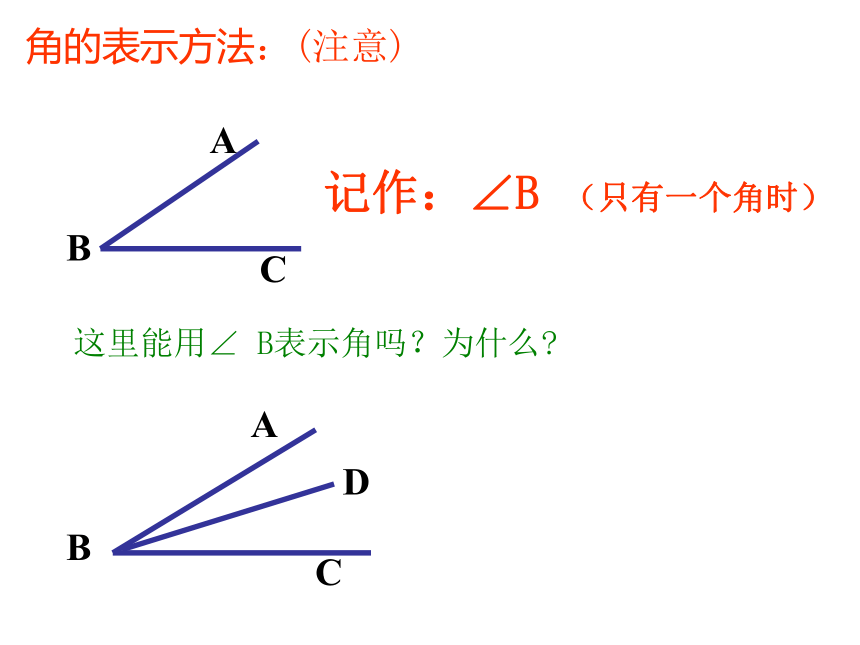
角的表示方法:(注意)
记作:∠B (只有一个角时)
A
B
C
A
B
C
D
这里能用∠ B表示角吗?为什么?
O
A
B
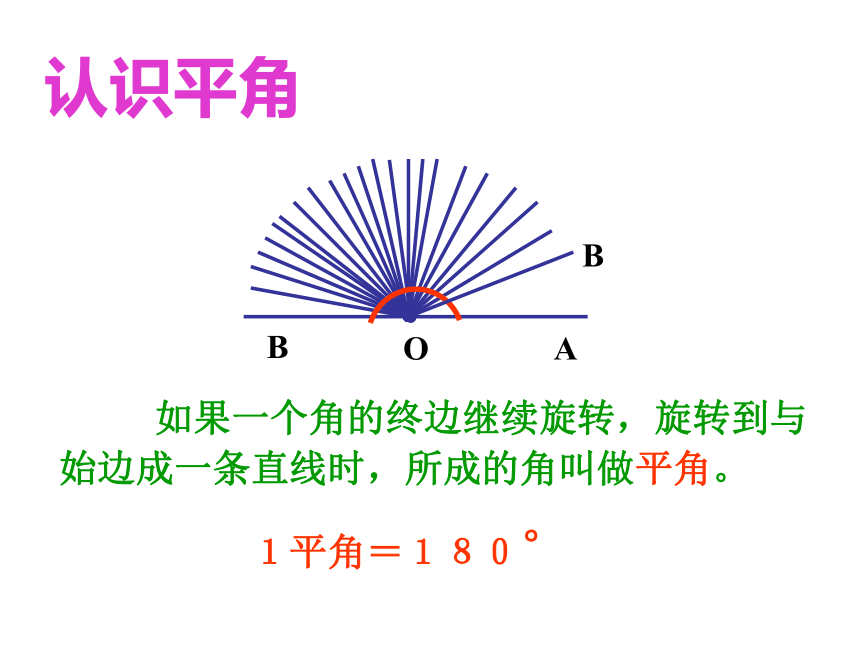
如果一个角的终边继续旋转,旋转到与始边成一条直线时,所成的角叫做平角。
1平角=180°
认识平角
B
O
A
(B)
当终边旋转到与始边重合时,所成的角叫做周角。
1周角=360°
认识周角
想一想:
小学我们还学过那些角?
练一练:
课本第122页 练习1
习题1
一判断题.
(1)两条射线组成的图形叫角。( )
(2)平角是一条直线。 ( )
(3)周角是一条射线。 ( )
(4)有一条射线旋转而成的图形叫做角。( )
(5)角的两边长短与角的大小无关。 ( )
×
×
×
×
√
∠1
∠ACB
∠BAC
∠ABC
将图中的角用不同方法表示出来,并填写下表:
2
1
B
A
D
C
E
做一做:
∠BAD
∠BCE
∠2
∠
∠
∠B
小组活动:
课本121页 做一做
角度制:
角的换算:
解:先把0.32 °化为分,
0.32 °=60′×0.32 =19 .2′
再把0.2′化为秒,
0.2′=60″× 0.2=12″
所以 57.32°=57 °19′12″
例 1 将 57.32°用度、分、秒表示。
用度、分、秒表示:
(1) 78.26 °
(2) 48.32 °
解:(1) 78.26°=78°15′36″
(2) 48.32°=48°19′12″
用度、分、秒表示:
(1)0.75 °
(2)( )°
1
8
小结:
想一想:本节课你有何收获?
1. 角的两种定义;
2. 角的四种表示方法;
3. 平角、周角;
4. 角的换算。
经过1小时,钟表的时针转过的角度是( ),分针转过的角度是( ),经过15分钟,分针转过的角度是( ),时针转过的角度是( )。
思考题:
答案:30°,360°,90°,7.5°
作业:
1 数学课本第123页: 4
2《点金教练》
再 见
本节学习目标:
角的两种定义及角的三种表示方法.
角的度量单位及角的换算.
生活中角的形象!
什么是角呢? 生活中有许多与角有关的实例,观察下图,你能指出图中的角吗?
角是由两条具有公共端点的射线组成的图形。
顶点
射线
射线
边
边
角的定义(静态)
角也可以看做一条射线绕端点旋转所组成的图形。
始边
终边
角的定义(动态)
角的表示方法
B
A
C
O
α
O
1
①记作:∠ABC 或∠CBA
② 记作:∠B
③记作∠α
④记作∠1
角用“∠”表示,读做“角”。注意:不要写成“ < ”.
角的表示方法有下面四种:
角的表示方法:(注意)
记作:∠B (只有一个角时)
A
B
C
A
B
C
D
这里能用∠ B表示角吗?为什么?
O
A
B
如果一个角的终边继续旋转,旋转到与始边成一条直线时,所成的角叫做平角。
1平角=180°
认识平角
B
O
A
(B)
当终边旋转到与始边重合时,所成的角叫做周角。
1周角=360°
认识周角
想一想:
小学我们还学过那些角?
练一练:
课本第122页 练习1
习题1
一判断题.
(1)两条射线组成的图形叫角。( )
(2)平角是一条直线。 ( )
(3)周角是一条射线。 ( )
(4)有一条射线旋转而成的图形叫做角。( )
(5)角的两边长短与角的大小无关。 ( )
×
×
×
×
√
∠1
∠ACB
∠BAC
∠ABC
将图中的角用不同方法表示出来,并填写下表:
2
1
B
A
D
C
E
做一做:
∠BAD
∠BCE
∠2
∠
∠
∠B
小组活动:
课本121页 做一做
角度制:
角的换算:
解:先把0.32 °化为分,
0.32 °=60′×0.32 =19 .2′
再把0.2′化为秒,
0.2′=60″× 0.2=12″
所以 57.32°=57 °19′12″
例 1 将 57.32°用度、分、秒表示。
用度、分、秒表示:
(1) 78.26 °
(2) 48.32 °
解:(1) 78.26°=78°15′36″
(2) 48.32°=48°19′12″
用度、分、秒表示:
(1)0.75 °
(2)( )°
1
8
小结:
想一想:本节课你有何收获?
1. 角的两种定义;
2. 角的四种表示方法;
3. 平角、周角;
4. 角的换算。
经过1小时,钟表的时针转过的角度是( ),分针转过的角度是( ),经过15分钟,分针转过的角度是( ),时针转过的角度是( )。
思考题:
答案:30°,360°,90°,7.5°
作业:
1 数学课本第123页: 4
2《点金教练》
再 见
