人教版九年级数学上册第二十三章第一节图形的旋转课时同步训练
文档属性
| 名称 | 人教版九年级数学上册第二十三章第一节图形的旋转课时同步训练 |

|
|
| 格式 | rar | ||
| 文件大小 | 430.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-18 00:00:00 | ||
图片预览



文档简介
登陆21世纪教育 助您教考全无忧
第二十三章 旋转
23.1 图形的旋转
第1课时
课前预习篇
1.旋转的概念
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动称为旋转.这个定点称为旋转中心,转过的这个角称为旋转角.
2.旋转不改变图形的大小和形状,只改变图形的位置.
3.平移和旋转的异同
(1)相同:都是一种运动;运动前后不改变图形的形状和大小
(2)不同点:平移是沿直线运动,运动量的大小由移动的距离决定;旋转是按顺时针或逆时针方向运动,运动量的大小由转动的角度决定.
典例剖析篇
【例1】如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
【解析】此题考查了对旋转、旋转中心、旋转角的理解.观察图形在旋转的过程中各部分的位置变化情况,发现点O的位置没有发生变化,即可确定点O是旋转中心,点A与点E,点B与点F分别为对应点,∠AOE与∠BOF都是旋转角.
【答案】(1)旋转中心是点O.
(2)点A移到了点E,点B移到了点F.
【例2】同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,如下图.是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心( )
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
【解析】要确定四边形的放旋转角度,只需找准其一边旋转的角度即可.AD边绕点A逆时针旋转120度得到AG边,因此四边形AEFG可以看作是四边形ABCD以A点为旋转中心,逆时针旋转120度得到的.
【答案】 D
基础夯实篇
1.在下列运动中,属于旋转的是( A )
①电风扇扇页的运动 ②转呼拉圈 ③转陀螺
④彩旗飘扬 ⑤跳蝇
A.①②③ B.②③
C.①③⑤ D. ②③⑤
2.下列关于旋转的描述,不正确的是( D )
A. 旋转时图形上每一点都绕旋转中心沿相同的方向转动了相同的角度
B.旋转时图形中的任意一对对应点与旋转中心的连线所成的角都相同
C.旋转时图形中的任意一对对应点到旋转中心的距离相等
D.旋转时图形中的任意一对对应点间的距离都等于定长
3.(2010珠海)现有如图1所示的四张牌,若只将其中一张牌旋转180°后得到图2,则旋转的牌是( B )
4.下列图形中,旋转60度可以与原图形重合的是( A )
A.正六边形 B.正五边形 C.正方形 D.正三角形
5.(2010咸宁)平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转得到,则点的坐标是( C )
A.(,3) B.(,4) C.(3,) D.(4,)
6.如下图,把矩形放在直角坐标系中,在轴上,在轴上,且,,把矩形绕着原点顺时针旋转得到矩形,则点的坐标为( C )
( http: / / )
A. B. C. D.
7.(2010永嘉)将点A(,0)绕着原点顺时针方向旋转60°得到点B,则点B的坐标是 (6,) .
8.(2009钦州)钟表分针的运动可看作是一种旋转现象,一只标准时钟的分针匀速旋转,经过15分钟旋转了_90_度.
9.(2009十堰)如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是 (4,-1) .
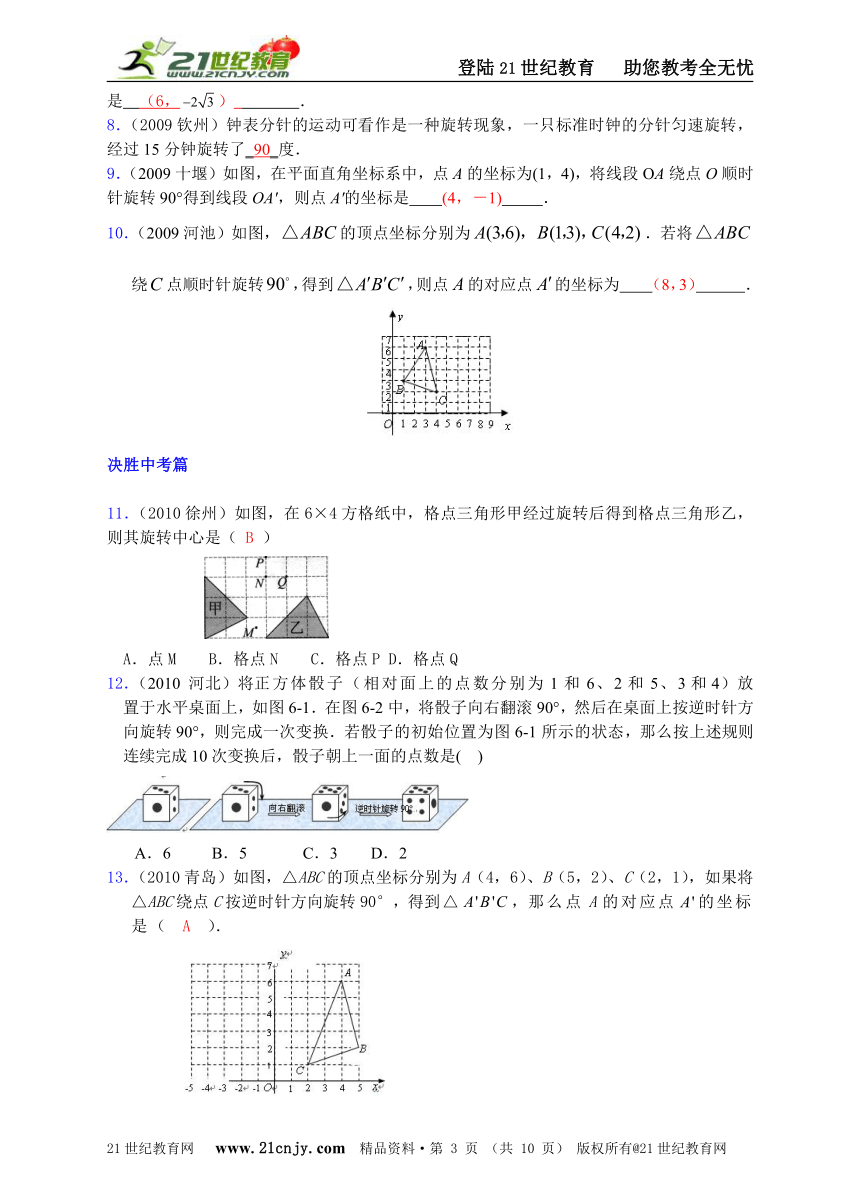
10.(2009河池)如图,的顶点坐标分别为.若将绕点顺时针旋转,得到,则点的对应点的坐标为 (8,3) .
决胜中考篇
11.(2010徐州)如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( B )
A.点M B.格点N C.格点P D.格点Q
12.(2010 河北)将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图6-1.在图6-2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图6-1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.2
13.(2010青岛)如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△,那么点A的对应点的坐标是( A ).
A.(-3,3) B.(3,-3) C.(-2,4) D.(1,4)
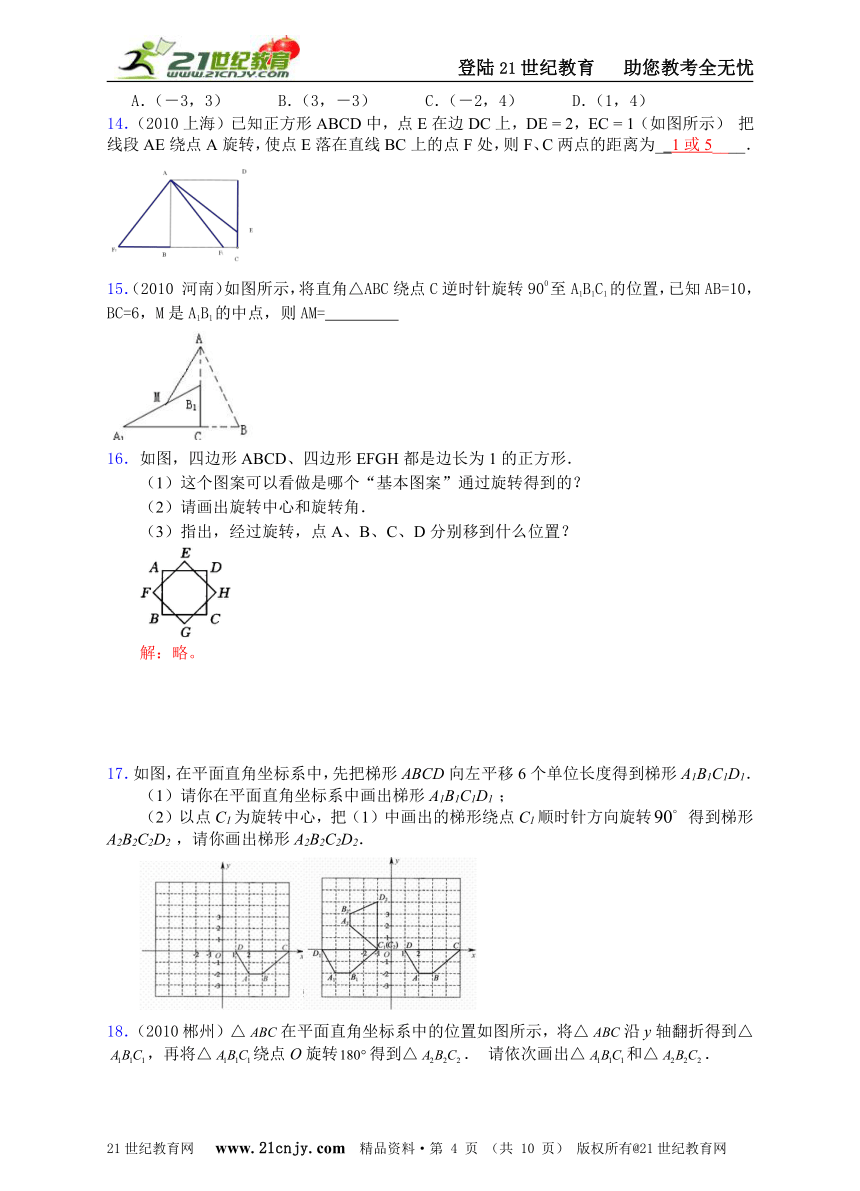
14.(2010上海)已知正方形ABCD中,点E在边DC上,DE = 2,EC = 1(如图所示) 把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为__1或5____.
15.(2010 河南)如图所示,将直角△ABC绕点C逆时针旋转900至A1B1C1的位置,已知AB=10,BC=6,M是A1B1的中点,则AM=
16.如图,四边形ABCD、四边形EFGH都是边长为1的正方形.
(1)这个图案可以看做是哪个“基本图案”通过旋转得到的?
(2)请画出旋转中心和旋转角.
(3)指出,经过旋转,点A、B、C、D分别移到什么位置?
( http: / / www. / )
解:略。
17.如图,在平面直角坐标系中,先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1.
(1)请你在平面直角坐标系中画出梯形A1B1C1D1 ;
(2)以点C1为旋转中心,把(1)中画出的梯形绕点C1顺时针方向旋转 得到梯形A2B2C2D2 ,请你画出梯形A2B2C2D2.
18.(2010郴州)△在平面直角坐标系中的位置如图所示,将△沿y轴翻折得到△,再将△绕点O旋转得到△. 请依次画出△和△.
19.(2010重庆)有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,……,则第10次旋转后得到的图形与图①~④中相同的是( B )
A.图① B.图② C.图③ D.图④
20.如图17所示是一种花瓣图案,它可以看作是一个什么“基本图案”形成的,试用两种方法分析其形成过程.
解:方法一:可看作整个花瓣的六分之一部分,图案为绕中心O依次旋转60°、120°、180°、240°、300°而得到整个图案.
方法二:可看作是绕中心O依次旋转60°、120°得到整个图案的.
方法三:可看作整个花瓣的一半绕中心O旋转180°得到的,也可看作是花瓣的一半.经过轴对称得到的
第2课时
课前预习篇
1. 旋转的性质
(1)旋转不改变图形的大小和形状.
(2)对应点到旋转中心的距离相等.
(3)对应点与旋转中心所连接线段的夹角等于旋转角.
(4)旋转前后的图形全等.
2.旋转的作图的步骤:
(1)找出图形的关键点;(2)确定旋转中心、旋转方向和旋转角;(3)将关键点与旋转中心连接起来,然后按旋转方向将它们旋转一个旋转角,得到关键点的对应点;(4)按照原图形的顺序连接这些对应点,所得图形就是旋转后的图形.
典例剖析篇
【例1】如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B对应点的位置,以及旋转后的三角形.
【解析】绕C点旋转,A点的对应点是D点,那么旋转角就是∠ACD,根据对应点与旋转中心所连线段的夹角等于旋转角,即∠BCB′=ACD,又由对应点到旋转中心的距离相等,即CB=CB′,就可确定B′的位置,如图所示.
( http: / / www. / )
解:(1)连接CD
(2)以CB为一边作∠BCE,使得∠BCE=∠ACD
(3)在射线CE上截取CB′=CB, 则B′即为所求的B的对应点.
(4)连接DB′. 则△DB′C就是△ABC绕C点旋转后的图形.
【例2】(2010台州)如图,菱形ABCD中,AB=2 ,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O所经过的路径总长为(结果保留π) .
【解析】由图得OA=,BO=1,菱形每3次操作是一次循环,中心O所经过的路径长为π×+π×1=(+)π.
所以菱形中心O所经过的路径总长为12(+)π=(8+4)π
【答案】(8+4)π
基础夯实篇
1.将正三角形绕其中心旋转,要使旋转后与自身重合,至少要旋转( B )
A.60° B.120° C.180° D.72°
2.在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是(B )
3.如图,这个图形旋转一周会与原图形重合几次?( )
A、0 B、1 C、2 D、4
5.(2010十堰)如图,将△ABC绕点C顺时针方向旋转40°得△A’CB’,若AC⊥A’B’,则∠BAC等于( A )
A.50° B.60° C.70° D.80°
6.如图3的方格纸中,左边图形到右边图形的变换是( D )
A.向右平移7格
B.以AB的垂直平分线为对称轴作轴对称,再以AB为对称轴作轴对称
C.绕AB的中点旋转1800,再以AB为对称轴作轴对称
D.以AB为对称轴作轴对称,再向右平移7格
7.下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( C )
A B C D
8.如图5所示,图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是( B )
A.l个 B.2个
C.3个 D.4个
9.(2010菏泽)如图,若将△ABC绕点 C, 顺时针旋转90°后得到,则A点的对应点的坐标是 .
10.如图1,△ABC是等腰直角三角形,D是AB上一点, △CBD经旋转后到达△ACE的位置,则旋转中心是__点C___;旋转角度是___90°__;点B的对应点是__点A___;点D的对应点是_点E____;线段CB的对应点是__CA___;∠B的对应角是__∠EAC____;如果点M是CB的,那么经过上述旋转后,点M移到了_____点N处____.
决胜中考篇
11.如图,ΔABC和ΔADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图7,再将图23—A—4作为“基本图形”绕着A点经过逆时针连续旋转得到图7.两次旋转的角度分别为( A )
A.45°,90° B.90°,45°
C.60°,30° D.30°,60
12. (2010杭州)如图,在△ABC中, ∠CAB=70°,. 在同一平面内, 将△ABC绕点A旋转到△AB′C′的位置, 使得CC′∥AB, 则∠BAB′= ( C )
A. 30° B. 35° C. 40° D. 50°
13.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是_____90 ____.
14.(2010天津)如图,已知正方形的边长为3,为边上一点, .以点为中心,把△顺时针旋转,得△,连接,则的长等于 .
15.如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L、M在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.
解:∵四边形ABCD、四边形AKLM是正方形,∴AB=AD,AK=AM,且∠BAD=∠KAM为旋转角且为90°
∴△ADM是以A为旋转中心,∠BAD为旋转角由△ABK旋转而成的
∴BK=DM
16.(2010台州)如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK___=____MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK_ >__MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK__ >_MK,证明你所得到的结论.
(3)如果,请直接写出∠CDF的度数和的值.
解:
证明:作点C关于FD的对称点G,
连接GK,GM,GD,
则CD=GD ,GK = CK,∠GDK=∠CDK,
∵D是AB的中点,∴AD=CD=GD.
∵30°,∴∠CDA=120°,
∵∠EDF=60°,∴∠GDM+∠GDK=60°,
∠ADM+∠CDK =60°.
∴∠ADM=∠GDM,
∵DM=DM,
∴△ADM≌△GDM,∴GM=AM.
∵GM+GK>MK,∴AM+CK>MK.
(3)∠CDF=15°,
17.如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:
(1)画出四边形ABCD旋转后的图形;
(2)求点C旋转过程事所经过的路径长;
(3)设点B旋转后的对应点为B’,求证:.
答案
(2)易知点C的旋转路径是以为O圆心,OC为半径的半圆
因为OC=,所以半圆的周长为π
(3)
,
所以
所以是直角三角形,
所以.
18. 如图,正方形ABCD的对角线相交于点O.点O是正方形A'B'C'O的一个顶点.如果两个正方形的边长相等,那么正方形A'B'C'O绕点O无论怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的1/4,想一想,为什么?
解:当四边形A'B'C'O旋转至如图1所示的位置时,阴部分△OBC的面积就是正方形ABCD面积的1/4.当正方形A'B'C'O顺时针旋转至图2所示的位置时,设OA′交AB于点E,OC′交BC于点F.因为OB=OC,且∠BOE=∠COF,∠OBE=∠OCF=45°,所以△BOE可以看作是△OCF绕点O顺时针旋转90得到的,点E与点F是对应点.由于旋转不改变图形的形状和大小,所以△BOE与△COF的面积相等,因此阴影部分的与△BOC的面积相等,阴影部他的面积也等于一个正方形面积的1/4.
图6
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 11 页) 版权所有@21世纪教育网
第二十三章 旋转
23.1 图形的旋转
第1课时
课前预习篇
1.旋转的概念
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动称为旋转.这个定点称为旋转中心,转过的这个角称为旋转角.
2.旋转不改变图形的大小和形状,只改变图形的位置.
3.平移和旋转的异同
(1)相同:都是一种运动;运动前后不改变图形的形状和大小
(2)不同点:平移是沿直线运动,运动量的大小由移动的距离决定;旋转是按顺时针或逆时针方向运动,运动量的大小由转动的角度决定.
典例剖析篇
【例1】如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
【解析】此题考查了对旋转、旋转中心、旋转角的理解.观察图形在旋转的过程中各部分的位置变化情况,发现点O的位置没有发生变化,即可确定点O是旋转中心,点A与点E,点B与点F分别为对应点,∠AOE与∠BOF都是旋转角.
【答案】(1)旋转中心是点O.
(2)点A移到了点E,点B移到了点F.
【例2】同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,如下图.是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心( )
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
【解析】要确定四边形的放旋转角度,只需找准其一边旋转的角度即可.AD边绕点A逆时针旋转120度得到AG边,因此四边形AEFG可以看作是四边形ABCD以A点为旋转中心,逆时针旋转120度得到的.
【答案】 D
基础夯实篇
1.在下列运动中,属于旋转的是( A )
①电风扇扇页的运动 ②转呼拉圈 ③转陀螺
④彩旗飘扬 ⑤跳蝇
A.①②③ B.②③
C.①③⑤ D. ②③⑤
2.下列关于旋转的描述,不正确的是( D )
A. 旋转时图形上每一点都绕旋转中心沿相同的方向转动了相同的角度
B.旋转时图形中的任意一对对应点与旋转中心的连线所成的角都相同
C.旋转时图形中的任意一对对应点到旋转中心的距离相等
D.旋转时图形中的任意一对对应点间的距离都等于定长
3.(2010珠海)现有如图1所示的四张牌,若只将其中一张牌旋转180°后得到图2,则旋转的牌是( B )
4.下列图形中,旋转60度可以与原图形重合的是( A )
A.正六边形 B.正五边形 C.正方形 D.正三角形
5.(2010咸宁)平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转得到,则点的坐标是( C )
A.(,3) B.(,4) C.(3,) D.(4,)
6.如下图,把矩形放在直角坐标系中,在轴上,在轴上,且,,把矩形绕着原点顺时针旋转得到矩形,则点的坐标为( C )
( http: / / )
A. B. C. D.
7.(2010永嘉)将点A(,0)绕着原点顺时针方向旋转60°得到点B,则点B的坐标是 (6,) .
8.(2009钦州)钟表分针的运动可看作是一种旋转现象,一只标准时钟的分针匀速旋转,经过15分钟旋转了_90_度.
9.(2009十堰)如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是 (4,-1) .
10.(2009河池)如图,的顶点坐标分别为.若将绕点顺时针旋转,得到,则点的对应点的坐标为 (8,3) .
决胜中考篇
11.(2010徐州)如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( B )
A.点M B.格点N C.格点P D.格点Q
12.(2010 河北)将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图6-1.在图6-2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图6-1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.2
13.(2010青岛)如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△,那么点A的对应点的坐标是( A ).
A.(-3,3) B.(3,-3) C.(-2,4) D.(1,4)
14.(2010上海)已知正方形ABCD中,点E在边DC上,DE = 2,EC = 1(如图所示) 把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为__1或5____.
15.(2010 河南)如图所示,将直角△ABC绕点C逆时针旋转900至A1B1C1的位置,已知AB=10,BC=6,M是A1B1的中点,则AM=
16.如图,四边形ABCD、四边形EFGH都是边长为1的正方形.
(1)这个图案可以看做是哪个“基本图案”通过旋转得到的?
(2)请画出旋转中心和旋转角.
(3)指出,经过旋转,点A、B、C、D分别移到什么位置?
( http: / / www. / )
解:略。
17.如图,在平面直角坐标系中,先把梯形ABCD向左平移6个单位长度得到梯形A1B1C1D1.
(1)请你在平面直角坐标系中画出梯形A1B1C1D1 ;
(2)以点C1为旋转中心,把(1)中画出的梯形绕点C1顺时针方向旋转 得到梯形A2B2C2D2 ,请你画出梯形A2B2C2D2.
18.(2010郴州)△在平面直角坐标系中的位置如图所示,将△沿y轴翻折得到△,再将△绕点O旋转得到△. 请依次画出△和△.
19.(2010重庆)有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,……,则第10次旋转后得到的图形与图①~④中相同的是( B )
A.图① B.图② C.图③ D.图④
20.如图17所示是一种花瓣图案,它可以看作是一个什么“基本图案”形成的,试用两种方法分析其形成过程.
解:方法一:可看作整个花瓣的六分之一部分,图案为绕中心O依次旋转60°、120°、180°、240°、300°而得到整个图案.
方法二:可看作是绕中心O依次旋转60°、120°得到整个图案的.
方法三:可看作整个花瓣的一半绕中心O旋转180°得到的,也可看作是花瓣的一半.经过轴对称得到的
第2课时
课前预习篇
1. 旋转的性质
(1)旋转不改变图形的大小和形状.
(2)对应点到旋转中心的距离相等.
(3)对应点与旋转中心所连接线段的夹角等于旋转角.
(4)旋转前后的图形全等.
2.旋转的作图的步骤:
(1)找出图形的关键点;(2)确定旋转中心、旋转方向和旋转角;(3)将关键点与旋转中心连接起来,然后按旋转方向将它们旋转一个旋转角,得到关键点的对应点;(4)按照原图形的顺序连接这些对应点,所得图形就是旋转后的图形.
典例剖析篇
【例1】如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B对应点的位置,以及旋转后的三角形.
【解析】绕C点旋转,A点的对应点是D点,那么旋转角就是∠ACD,根据对应点与旋转中心所连线段的夹角等于旋转角,即∠BCB′=ACD,又由对应点到旋转中心的距离相等,即CB=CB′,就可确定B′的位置,如图所示.
( http: / / www. / )
解:(1)连接CD
(2)以CB为一边作∠BCE,使得∠BCE=∠ACD
(3)在射线CE上截取CB′=CB, 则B′即为所求的B的对应点.
(4)连接DB′. 则△DB′C就是△ABC绕C点旋转后的图形.
【例2】(2010台州)如图,菱形ABCD中,AB=2 ,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O所经过的路径总长为(结果保留π) .
【解析】由图得OA=,BO=1,菱形每3次操作是一次循环,中心O所经过的路径长为π×+π×1=(+)π.
所以菱形中心O所经过的路径总长为12(+)π=(8+4)π
【答案】(8+4)π
基础夯实篇
1.将正三角形绕其中心旋转,要使旋转后与自身重合,至少要旋转( B )
A.60° B.120° C.180° D.72°
2.在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是(B )
3.如图,这个图形旋转一周会与原图形重合几次?( )
A、0 B、1 C、2 D、4
5.(2010十堰)如图,将△ABC绕点C顺时针方向旋转40°得△A’CB’,若AC⊥A’B’,则∠BAC等于( A )
A.50° B.60° C.70° D.80°
6.如图3的方格纸中,左边图形到右边图形的变换是( D )
A.向右平移7格
B.以AB的垂直平分线为对称轴作轴对称,再以AB为对称轴作轴对称
C.绕AB的中点旋转1800,再以AB为对称轴作轴对称
D.以AB为对称轴作轴对称,再向右平移7格
7.下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( C )
A B C D
8.如图5所示,图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是( B )
A.l个 B.2个
C.3个 D.4个
9.(2010菏泽)如图,若将△ABC绕点 C, 顺时针旋转90°后得到,则A点的对应点的坐标是 .
10.如图1,△ABC是等腰直角三角形,D是AB上一点, △CBD经旋转后到达△ACE的位置,则旋转中心是__点C___;旋转角度是___90°__;点B的对应点是__点A___;点D的对应点是_点E____;线段CB的对应点是__CA___;∠B的对应角是__∠EAC____;如果点M是CB的,那么经过上述旋转后,点M移到了_____点N处____.
决胜中考篇
11.如图,ΔABC和ΔADE都是等腰直角三角形,∠C和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图7,再将图23—A—4作为“基本图形”绕着A点经过逆时针连续旋转得到图7.两次旋转的角度分别为( A )
A.45°,90° B.90°,45°
C.60°,30° D.30°,60
12. (2010杭州)如图,在△ABC中, ∠CAB=70°,. 在同一平面内, 将△ABC绕点A旋转到△AB′C′的位置, 使得CC′∥AB, 则∠BAB′= ( C )
A. 30° B. 35° C. 40° D. 50°
13.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是_____90 ____.
14.(2010天津)如图,已知正方形的边长为3,为边上一点, .以点为中心,把△顺时针旋转,得△,连接,则的长等于 .
15.如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L、M在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.
解:∵四边形ABCD、四边形AKLM是正方形,∴AB=AD,AK=AM,且∠BAD=∠KAM为旋转角且为90°
∴△ADM是以A为旋转中心,∠BAD为旋转角由△ABK旋转而成的
∴BK=DM
16.(2010台州)如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK___=____MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK_ >__MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK__ >_MK,证明你所得到的结论.
(3)如果,请直接写出∠CDF的度数和的值.
解:
证明:作点C关于FD的对称点G,
连接GK,GM,GD,
则CD=GD ,GK = CK,∠GDK=∠CDK,
∵D是AB的中点,∴AD=CD=GD.
∵30°,∴∠CDA=120°,
∵∠EDF=60°,∴∠GDM+∠GDK=60°,
∠ADM+∠CDK =60°.
∴∠ADM=∠GDM,
∵DM=DM,
∴△ADM≌△GDM,∴GM=AM.
∵GM+GK>MK,∴AM+CK>MK.
(3)∠CDF=15°,
17.如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:
(1)画出四边形ABCD旋转后的图形;
(2)求点C旋转过程事所经过的路径长;
(3)设点B旋转后的对应点为B’,求证:.
答案
(2)易知点C的旋转路径是以为O圆心,OC为半径的半圆
因为OC=,所以半圆的周长为π
(3)
,
所以
所以是直角三角形,
所以.
18. 如图,正方形ABCD的对角线相交于点O.点O是正方形A'B'C'O的一个顶点.如果两个正方形的边长相等,那么正方形A'B'C'O绕点O无论怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的1/4,想一想,为什么?
解:当四边形A'B'C'O旋转至如图1所示的位置时,阴部分△OBC的面积就是正方形ABCD面积的1/4.当正方形A'B'C'O顺时针旋转至图2所示的位置时,设OA′交AB于点E,OC′交BC于点F.因为OB=OC,且∠BOE=∠COF,∠OBE=∠OCF=45°,所以△BOE可以看作是△OCF绕点O顺时针旋转90得到的,点E与点F是对应点.由于旋转不改变图形的形状和大小,所以△BOE与△COF的面积相等,因此阴影部分的与△BOC的面积相等,阴影部他的面积也等于一个正方形面积的1/4.
图6
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 11 页) 版权所有@21世纪教育网
同课章节目录
