人教版八年级上册数学13.4 课题学习 造桥选址问题 课件(15张PPT)
文档属性
| 名称 | 人教版八年级上册数学13.4 课题学习 造桥选址问题 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
13.4
课题学习
最短路径问题(2)
造桥选址问题
教学目标
1、知识与技能:
理解利用平移的方法,解决最短路径问题。
2、过程与方法:
(1)在观察、操作、归纳等探索过程中,培养学生的实际动手能力;
(2)在运用知识解决有关问题的过程中,体验并掌握探索、归纳最短路径选取的方法。
3、情感、态度与价值观
(1)体会数学与现实生活的联系,增强克服困难的勇气和信心;
(2)会应用数学知识解决一些简单的实际问题,增强应用意识;
(3)使学生进一步形成数学来源于实践,反过来又服务于实践的辩证唯物主义观点。
1、
两点所有的连线中线段最短。
2、
连接直线外一点与直线上各点的
所有线段中,垂线段最短。
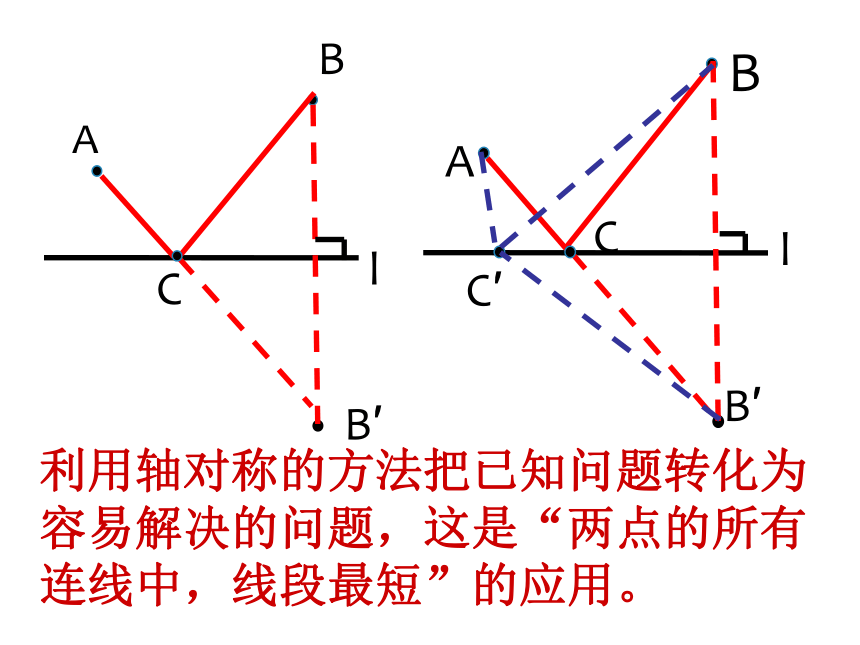
应用1:利用轴对称的方法解决最短路径选取问题。
知识点回顾
B′
l
A
B
C
利用轴对称的方法把已知问题转化为容易解决的问题,这是“两点的所有连线中,线段最短”的应用。
B′
l
A
B
C
C′
如果把一条直线l变成两条直线,会变成生活中的什么问题呢?
提出问题
茅以升简介
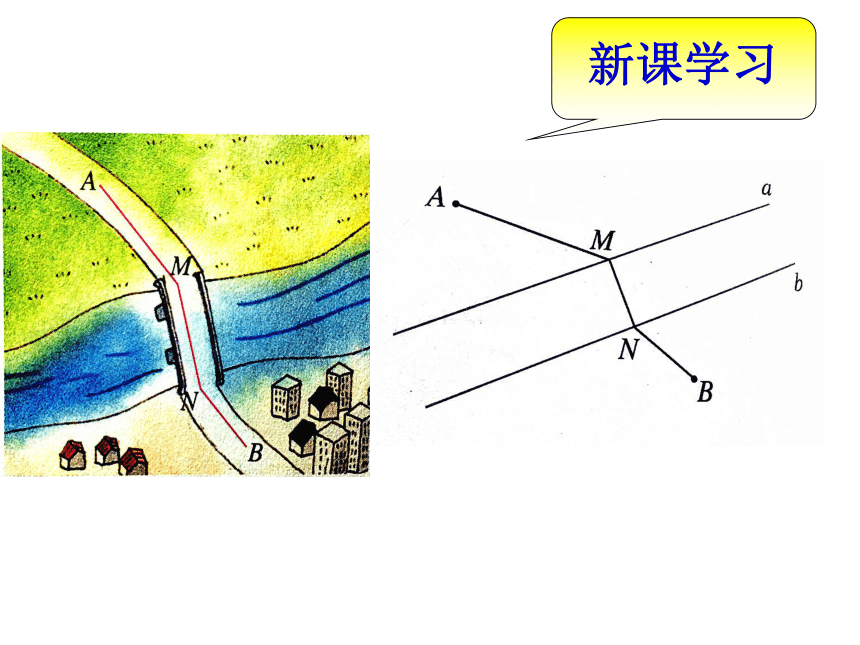
新课学习
A
B
M
N
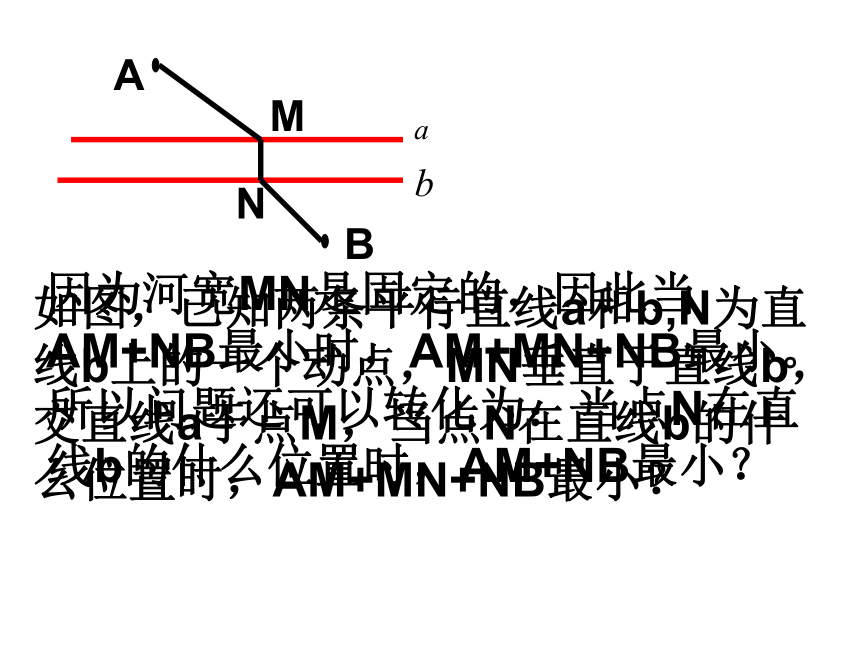
如图,已知两条平行直线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M,当点N在直线b的什么位置时,AM+MN+NB最小?
思维分析
因为河宽MN是固定的,因此当AM+NB最小时,AM+MN+NB最小。所以问题还可以转化为:当点N在直线b的什么位置时,AM+NB最小?
拓展1:如图,如果A、B两地之间有两条平行的河,我们要建的桥都是与河岸垂直的。我们如何找到这个最短的距离呢?
拓展应用
河流1
河流2
A
B
方法
图像
方法:将点A沿与第一条河流垂直的方向平移一个河宽到A1,将B沿与第二条河垂直的方向平移一个河宽到B1,连接A1B1与两条河分别相交于P、M,在P、M两处,分别建桥PQ
、
MN,所得路径AQPMNB最短。
返回
图像
A
B
P
Q
M
N
AQPMNB的路程最短
返回
拓展2:如图,荆州古城河在CC`处直角拐弯,从A处到达B处,需经两座桥:DD`,EE`(桥宽不计),设护城河以及两座桥都是东西、南北方向的,如何架桥可使ADD`E`EB的路程最短?
方法
图像
方法:把点A沿与东西方向的河流垂直的方向平移一个河宽到A`,把点B沿着南北方向的河流垂直的方向平移一个河宽到B`,连接A`B`,与两河分别于D`和E`,在D`和E`处分别建桥DD`和EE`,所得路程ADD`E`EB最短。
返回
图像
B
A
E`
E
D`
D
B`
此时,ADD`E`EB的路程最短。
A`
B
A
B
A
返回
造桥选址问题,要使所得到的路径最短,就是要通过平移,使得除桥长不变外,把其它路径平移在一条直线上,从而做出最短路径的选择。这是“两点所有的连线中,线段最短”的第二个应用。
小结
谢谢!
13.4
课题学习
最短路径问题(2)
造桥选址问题
教学目标
1、知识与技能:
理解利用平移的方法,解决最短路径问题。
2、过程与方法:
(1)在观察、操作、归纳等探索过程中,培养学生的实际动手能力;
(2)在运用知识解决有关问题的过程中,体验并掌握探索、归纳最短路径选取的方法。
3、情感、态度与价值观
(1)体会数学与现实生活的联系,增强克服困难的勇气和信心;
(2)会应用数学知识解决一些简单的实际问题,增强应用意识;
(3)使学生进一步形成数学来源于实践,反过来又服务于实践的辩证唯物主义观点。
1、
两点所有的连线中线段最短。
2、
连接直线外一点与直线上各点的
所有线段中,垂线段最短。
应用1:利用轴对称的方法解决最短路径选取问题。
知识点回顾
B′
l
A
B
C
利用轴对称的方法把已知问题转化为容易解决的问题,这是“两点的所有连线中,线段最短”的应用。
B′
l
A
B
C
C′
如果把一条直线l变成两条直线,会变成生活中的什么问题呢?
提出问题
茅以升简介
新课学习
A
B
M
N
如图,已知两条平行直线a和b,N为直线b上的一个动点,MN垂直于直线b,交直线a于点M,当点N在直线b的什么位置时,AM+MN+NB最小?
思维分析
因为河宽MN是固定的,因此当AM+NB最小时,AM+MN+NB最小。所以问题还可以转化为:当点N在直线b的什么位置时,AM+NB最小?
拓展1:如图,如果A、B两地之间有两条平行的河,我们要建的桥都是与河岸垂直的。我们如何找到这个最短的距离呢?
拓展应用
河流1
河流2
A
B
方法
图像
方法:将点A沿与第一条河流垂直的方向平移一个河宽到A1,将B沿与第二条河垂直的方向平移一个河宽到B1,连接A1B1与两条河分别相交于P、M,在P、M两处,分别建桥PQ
、
MN,所得路径AQPMNB最短。
返回
图像
A
B
P
Q
M
N
AQPMNB的路程最短
返回
拓展2:如图,荆州古城河在CC`处直角拐弯,从A处到达B处,需经两座桥:DD`,EE`(桥宽不计),设护城河以及两座桥都是东西、南北方向的,如何架桥可使ADD`E`EB的路程最短?
方法
图像
方法:把点A沿与东西方向的河流垂直的方向平移一个河宽到A`,把点B沿着南北方向的河流垂直的方向平移一个河宽到B`,连接A`B`,与两河分别于D`和E`,在D`和E`处分别建桥DD`和EE`,所得路程ADD`E`EB最短。
返回
图像
B
A
E`
E
D`
D
B`
此时,ADD`E`EB的路程最短。
A`
B
A
B
A
返回
造桥选址问题,要使所得到的路径最短,就是要通过平移,使得除桥长不变外,把其它路径平移在一条直线上,从而做出最短路径的选择。这是“两点所有的连线中,线段最短”的第二个应用。
小结
谢谢!
