2020-2021学年度湘教版九年级数学下册 第二学期 期中测试卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年度湘教版九年级数学下册 第二学期 期中测试卷(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 00:00:00 | ||
图片预览




文档简介
湘教版九年级数学下册
第二学期
期中测试卷
一、选择题(每题3分,共24分)
1.下列关于抛物线y=(x+2)2+6的说法正确的是( )
A.开口向下
B.顶点坐标为(2,6)
C.对称轴是直线x=2
D.与y轴的交点为(0,10)
2.有下列结论:(1)三点确定一个圆;(2)平分弦的直径垂直于弦;(3)三角形的外心到三角形各边的距离相等.其中正确的有( )
A.0个
B.1个
C.2个
D.3个
3.已知二次函数y=3(x-2)2+5,则有( )
A.当x>-2时,y随x的增大而减小
B.当x>-2时,y随x的增大而增大
C.当x>2时,y随x的增大而减小
D.当x>2时,y随x的增大而增大
4.如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点,已知,的度数分别为88°,32°,则∠P的度数为( )
A.26°
B.28°
C.30°
D.32°
5.如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为( )
A.40°
B.50°
C.65°
D.75°
6.已知A(-1,y1)、B(2,y2)、C(-3,y3)在函数y=-5(x+1)2+3的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y1<y3<y2
C.y2<y3<y1
D.y3<y2<y1
7.如图,在平面直角坐标系中,点A,B均在函数y=(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
A.(2,2)
B.(2,3)
C.(3,2)
D.
8.已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
A.ac>0
B.当x>0时,y随x的增大而减小
C.2a-b=0
D.方程ax2+bx+c=0的两根是x1=-1,x2=3
二、填空题(每题4分,共32分)
9.如图,∠AOB=60°,则∠ACB等于________.
10.如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为________.
11.已知△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径画圆,使得点A在⊙C内,点B在⊙C外,则半径r的取值范围是________.
12.若抛物线y=3x2-6x+a与x轴只有一个公共点,则a的值为________.
13.已知扇形的弧长为8π,圆心角为60°,则它的半径为________.
14.已知二次函数y=ax2+bx+c(a≠0)中,自变量x与函数y的部分对应值如下表:
x
…
-1
0
1
2
…
y
…
0
3
4
3
…
则当y>0时,x的取值范围是________.
15.边长为5的正六边形内接于⊙M,则⊙M的面积是________.
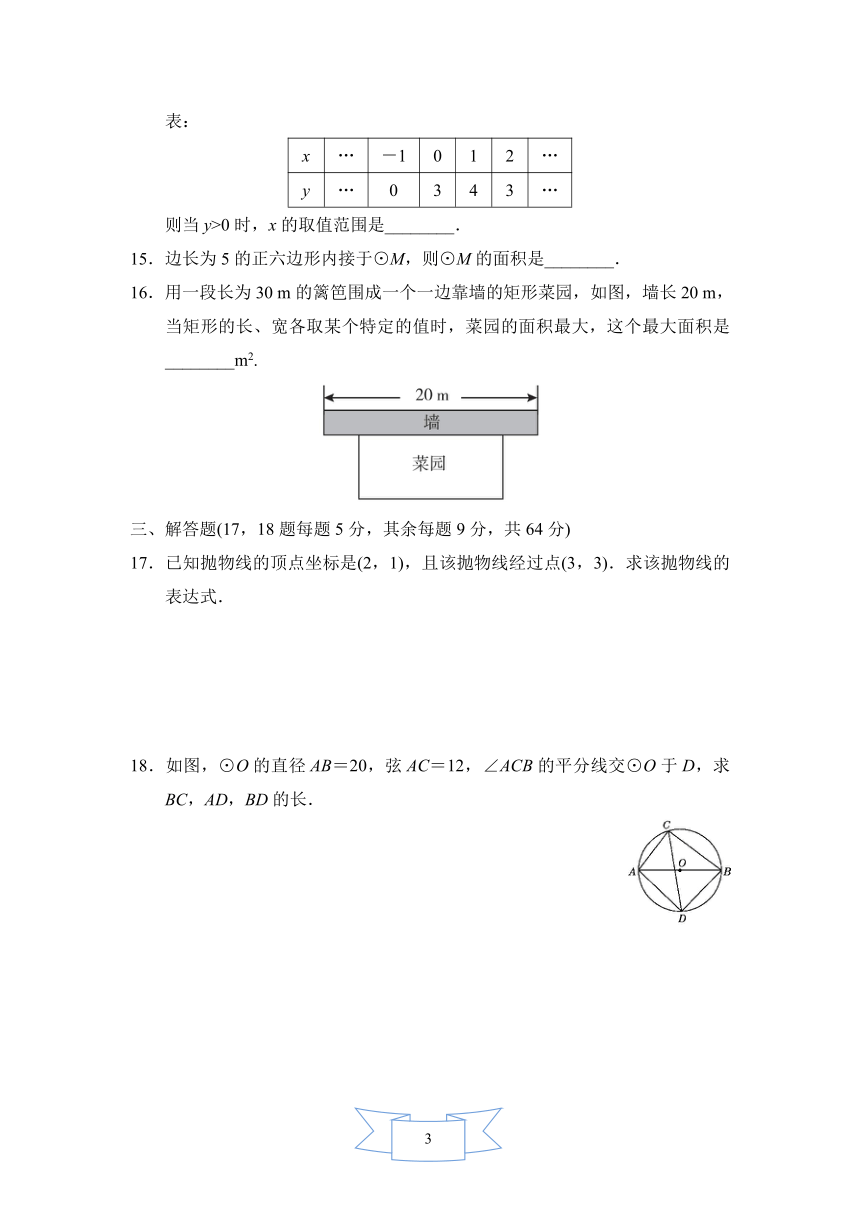
16.用一段长为30
m的篱笆围成一个一边靠墙的矩形菜园,如图,墙长20
m,当矩形的长、宽各取某个特定的值时,菜园的面积最大,这个最大面积是________m2.
三、解答题(17,18题每题5分,其余每题9分,共64分)
17.已知抛物线的顶点坐标是(2,1),且该抛物线经过点(3,3).求该抛物线的表达式.
18.如图,⊙O的直径AB=20,弦AC=12,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
19.如图,二次函数y=-x2+x+3的图象与x轴交于点A,B(点B在点A右侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求△ABC的面积.
20.如图,在△ABC中,AB=AC,以边BC为直径的⊙O与边AB交于点D,与边AC交于点E,连接OD,OE.
(1)求证:CE=BD;
(2)若∠C=55°,BC=10,求扇形ODE的面积.
21.如图,在平面直角坐标系xOy中,点A的坐标是(3,3),点B的坐标是(4,0),点C的坐标是(0,-1).
(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A′B′C;
(2)在(1)的条件下,①求出点A经过的路径的长(结果保留π);②写出点B′的坐标.
22.某商店经销一种双肩包,已知这种双肩包的成本价为每个30元,市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数表达式;
(2)当这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
23.如图,已知△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F,连接DF.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
24.如图①,已知抛物线y=-x2+bx+c经过A(1,0),B(-3,0)两点,且与y轴交于点C.
(1)求b,c的值;
(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由;
(3)如图②,点E为线段BC上一个动点(不与B,C重合),经过B,E,O三点的圆与过点B且垂直于BC的直线交于点F,当△OEF的面积取得最小值时,求点E的坐标.
答案
一、1.D 2.A 3.D 4.B 5.C 6.C
7.C 点拨:将点B的坐标代入反比例函数的表达式得k=6,则反比例函数的表达式是y=.∵点B的坐标为(1,6),⊙B与y轴相切,∴⊙B的半径是1,∴⊙A的半径是2,把y=2代入y=,得x=3,则点A的坐标是(3,2).
8.D 点拨:由二次函数y=ax2+bx+c的图象可得:抛物线开口向下,则a<0,抛物线与y轴的交点在y轴正半轴,则c>0,∴ac<0,选项A错误;由函数图象可得:当0<x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小,故选项B错误;∵对称轴为直线x=1,∴-=1,即2a+b=0,选项C错误;由图象可得抛物线与x轴的一个交点为(3,0),又对称轴为直线x=1,∴抛物线与x轴的另一个交点为(-1,0),则方程ax2+bx+c=0的两根是x1=-1,x2=3,选项D正确.
二、9.30° 10.110° 11.3<r<4 12.3
13.24 14.-1<x<3 15.25π 16.
三、17.解:∵抛物线的顶点坐标是(2,1),
∴设该抛物线的表达式为y=a(x-2)2+1,
又抛物线经过点(3,3).
∴3=a(3-2)2+1,解得a=2,
∴该抛物线的表达式是y=2(x-2)2+1.
18.解:∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∴BC==16.
∵CD是∠ACB的平分线,
∴∠ACD=∠DCB=45°,
∴∠DBA=∠DAB=45°.
在Rt△ABD中,sin
45°=,
∴AD=×AB=10
.
∴AD=BD=10
.
19.解:(1)∵二次函数y=-x2+x+3=-(x-4)(x+1),
∴当x=0时,y=3,当y=0时,x1=4,x2=-1,
即点A的坐标为(-1,0),点B的坐标为(4,0),点C的坐标为(0,3).
(2)由(1)得,AB=5,OC=3,
∴△ABC的面积===.
20.(1)证明:∵AB=AC,∴∠B=∠C,
∴=,∴=,∴CE=BD.
(2)解:∵∠C=55°,∴∠B=∠C=55°.
∵OB=OD,OC=OE,
∴∠B=∠ODB=55°,∠C=∠OEC=55°,
∴∠BOD=∠EOC=70°,
∴∠DOE=40°,∴S扇形ODE==.
21.解:(1)如图所示,△A′B′C即为所求.
INCLUDEPICTURE
"../AppData/Local/Temp/Rar$DIa0.421/19XJDB603.tif"
\
MERGEFORMAT
INCLUDEPICTURE
"F:\\21春初中\\数学\\九年级数学下(XJ版)\\word\\19XJDB603.tif"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\21春初中\\数学\\九年级数学下(XJ版)\\word\\19XJDB603.tif"
\
MERGEFORMATINET
(2)①如图,∵AC==5,∠ACA′=90°,
∴点A经过的路径的长为=.
②由图知点B′的坐标为(-1,3).
22.解:(1)由题意得w=(x-30)·y=(x-30)(-x+60)=-x2+30x+60x-1
800=-x2+90x-1
800,
即w与x之间的函数表达式为w=-x2+90x-1
800.
(2)w=-x2+90x-1
800=-(x-45)2+225,-1<0,∴当x=45时,w取得最大值,最大值是225.即当这种双肩包销售单价定为45元时,每天的销售利润最大,最大利润是225元.
(3)当w=200时,-x2+90x-1
800=200,解得x1=40,x2=50(不符合题意,舍去).
答:销售单价应定为40元.
23.(1)证明:连接OE,则OB=OE.
∵△ABC是等边三角形,∴∠ABC=∠C=60°.
∴△OBE是等边三角形.∴∠OEB=∠C=60°.∴OE∥AC.
∵EF⊥AC,∴EF⊥OE.又OE是⊙O的半径,∴直线EF是⊙O的切线.
(2)解:∵DF是⊙O的切线,∴∠ADF=90°.
设⊙O的半径为r,则BE=r,EC=4-r,AD=4-2r.
在Rt△ADF中,
∵∠A=60°,∴∠AFD=30°.∴AF=2AD=8-4r.∴FC=4-(8-4r)=4r-4.
在Rt△CEF中,
∵∠C=60°,∴∠CEF=30°.∴EC=2FC.
∴4-r=2(4r-4),解得r=.∴⊙O的半径是.
24.解:(1)把A(1,0),B(-3,0)的坐标代入y=-x2+bx+c,
得解得
(2)存在.作PD∥y轴交BC于D,设直线BC的表达式为y=mx+n.
由(1)易知C(0,3).
把点B(-3,0),C(0,3)的坐标分别代入y=mx+n,
得解得
故直线BC的表达式为y=x+3,
设点P的坐标为(x,-x2-2x+3)(-3<x<0),则点D的坐标为(x,x+3),
∴PD=-x2-2x+3-(x+3)=-x2-3x,
∴S△BPC=S△PBD+S△CPD=×3×(-x2-3x)=-x2-x=-+,
当x=-时,△BPC的面积最大,此时S△BPC=,
把x=-代入y=-x2-2x+3,得y=,∴点P的坐标为.
(3)∵OB=OC=3,
∴△OBC为等腰直角三角形,∴∠OBC=∠OCB=45°.
∵BF⊥BE,∴∠FBO=45°,∴∠OEF=∠OBF=45°,∠OFE=∠OBE=45°,
∴△OEF为等腰直角三角形,∴OE=OF,∠EOF=90°,
∴S△OEF=OE·OF=OE2,
∴当OE最小时,△OEF的面积取得最小值.
∵点E在线段BC上,
∴当OE⊥BC时,OE最小,此时点E是BC的中点,∴E.
第二学期
期中测试卷
一、选择题(每题3分,共24分)
1.下列关于抛物线y=(x+2)2+6的说法正确的是( )
A.开口向下
B.顶点坐标为(2,6)
C.对称轴是直线x=2
D.与y轴的交点为(0,10)
2.有下列结论:(1)三点确定一个圆;(2)平分弦的直径垂直于弦;(3)三角形的外心到三角形各边的距离相等.其中正确的有( )
A.0个
B.1个
C.2个
D.3个
3.已知二次函数y=3(x-2)2+5,则有( )
A.当x>-2时,y随x的增大而减小
B.当x>-2时,y随x的增大而增大
C.当x>2时,y随x的增大而减小
D.当x>2时,y随x的增大而增大
4.如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点,已知,的度数分别为88°,32°,则∠P的度数为( )
A.26°
B.28°
C.30°
D.32°
5.如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为( )
A.40°
B.50°
C.65°
D.75°
6.已知A(-1,y1)、B(2,y2)、C(-3,y3)在函数y=-5(x+1)2+3的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y1<y3<y2
C.y2<y3<y1
D.y3<y2<y1
7.如图,在平面直角坐标系中,点A,B均在函数y=(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
A.(2,2)
B.(2,3)
C.(3,2)
D.
8.已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
A.ac>0
B.当x>0时,y随x的增大而减小
C.2a-b=0
D.方程ax2+bx+c=0的两根是x1=-1,x2=3
二、填空题(每题4分,共32分)
9.如图,∠AOB=60°,则∠ACB等于________.
10.如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为________.
11.已知△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径画圆,使得点A在⊙C内,点B在⊙C外,则半径r的取值范围是________.
12.若抛物线y=3x2-6x+a与x轴只有一个公共点,则a的值为________.
13.已知扇形的弧长为8π,圆心角为60°,则它的半径为________.
14.已知二次函数y=ax2+bx+c(a≠0)中,自变量x与函数y的部分对应值如下表:
x
…
-1
0
1
2
…
y
…
0
3
4
3
…
则当y>0时,x的取值范围是________.
15.边长为5的正六边形内接于⊙M,则⊙M的面积是________.
16.用一段长为30
m的篱笆围成一个一边靠墙的矩形菜园,如图,墙长20
m,当矩形的长、宽各取某个特定的值时,菜园的面积最大,这个最大面积是________m2.
三、解答题(17,18题每题5分,其余每题9分,共64分)
17.已知抛物线的顶点坐标是(2,1),且该抛物线经过点(3,3).求该抛物线的表达式.
18.如图,⊙O的直径AB=20,弦AC=12,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
19.如图,二次函数y=-x2+x+3的图象与x轴交于点A,B(点B在点A右侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)求△ABC的面积.
20.如图,在△ABC中,AB=AC,以边BC为直径的⊙O与边AB交于点D,与边AC交于点E,连接OD,OE.
(1)求证:CE=BD;
(2)若∠C=55°,BC=10,求扇形ODE的面积.
21.如图,在平面直角坐标系xOy中,点A的坐标是(3,3),点B的坐标是(4,0),点C的坐标是(0,-1).
(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A′B′C;
(2)在(1)的条件下,①求出点A经过的路径的长(结果保留π);②写出点B′的坐标.
22.某商店经销一种双肩包,已知这种双肩包的成本价为每个30元,市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数表达式;
(2)当这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
23.如图,已知△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F,连接DF.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
24.如图①,已知抛物线y=-x2+bx+c经过A(1,0),B(-3,0)两点,且与y轴交于点C.
(1)求b,c的值;
(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由;
(3)如图②,点E为线段BC上一个动点(不与B,C重合),经过B,E,O三点的圆与过点B且垂直于BC的直线交于点F,当△OEF的面积取得最小值时,求点E的坐标.
答案
一、1.D 2.A 3.D 4.B 5.C 6.C
7.C 点拨:将点B的坐标代入反比例函数的表达式得k=6,则反比例函数的表达式是y=.∵点B的坐标为(1,6),⊙B与y轴相切,∴⊙B的半径是1,∴⊙A的半径是2,把y=2代入y=,得x=3,则点A的坐标是(3,2).
8.D 点拨:由二次函数y=ax2+bx+c的图象可得:抛物线开口向下,则a<0,抛物线与y轴的交点在y轴正半轴,则c>0,∴ac<0,选项A错误;由函数图象可得:当0<x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小,故选项B错误;∵对称轴为直线x=1,∴-=1,即2a+b=0,选项C错误;由图象可得抛物线与x轴的一个交点为(3,0),又对称轴为直线x=1,∴抛物线与x轴的另一个交点为(-1,0),则方程ax2+bx+c=0的两根是x1=-1,x2=3,选项D正确.
二、9.30° 10.110° 11.3<r<4 12.3
13.24 14.-1<x<3 15.25π 16.
三、17.解:∵抛物线的顶点坐标是(2,1),
∴设该抛物线的表达式为y=a(x-2)2+1,
又抛物线经过点(3,3).
∴3=a(3-2)2+1,解得a=2,
∴该抛物线的表达式是y=2(x-2)2+1.
18.解:∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∴BC==16.
∵CD是∠ACB的平分线,
∴∠ACD=∠DCB=45°,
∴∠DBA=∠DAB=45°.
在Rt△ABD中,sin
45°=,
∴AD=×AB=10
.
∴AD=BD=10
.
19.解:(1)∵二次函数y=-x2+x+3=-(x-4)(x+1),
∴当x=0时,y=3,当y=0时,x1=4,x2=-1,
即点A的坐标为(-1,0),点B的坐标为(4,0),点C的坐标为(0,3).
(2)由(1)得,AB=5,OC=3,
∴△ABC的面积===.
20.(1)证明:∵AB=AC,∴∠B=∠C,
∴=,∴=,∴CE=BD.
(2)解:∵∠C=55°,∴∠B=∠C=55°.
∵OB=OD,OC=OE,
∴∠B=∠ODB=55°,∠C=∠OEC=55°,
∴∠BOD=∠EOC=70°,
∴∠DOE=40°,∴S扇形ODE==.
21.解:(1)如图所示,△A′B′C即为所求.
INCLUDEPICTURE
"../AppData/Local/Temp/Rar$DIa0.421/19XJDB603.tif"
\
MERGEFORMAT
INCLUDEPICTURE
"F:\\21春初中\\数学\\九年级数学下(XJ版)\\word\\19XJDB603.tif"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\21春初中\\数学\\九年级数学下(XJ版)\\word\\19XJDB603.tif"
\
MERGEFORMATINET
(2)①如图,∵AC==5,∠ACA′=90°,
∴点A经过的路径的长为=.
②由图知点B′的坐标为(-1,3).
22.解:(1)由题意得w=(x-30)·y=(x-30)(-x+60)=-x2+30x+60x-1
800=-x2+90x-1
800,
即w与x之间的函数表达式为w=-x2+90x-1
800.
(2)w=-x2+90x-1
800=-(x-45)2+225,-1<0,∴当x=45时,w取得最大值,最大值是225.即当这种双肩包销售单价定为45元时,每天的销售利润最大,最大利润是225元.
(3)当w=200时,-x2+90x-1
800=200,解得x1=40,x2=50(不符合题意,舍去).
答:销售单价应定为40元.
23.(1)证明:连接OE,则OB=OE.
∵△ABC是等边三角形,∴∠ABC=∠C=60°.
∴△OBE是等边三角形.∴∠OEB=∠C=60°.∴OE∥AC.
∵EF⊥AC,∴EF⊥OE.又OE是⊙O的半径,∴直线EF是⊙O的切线.
(2)解:∵DF是⊙O的切线,∴∠ADF=90°.
设⊙O的半径为r,则BE=r,EC=4-r,AD=4-2r.
在Rt△ADF中,
∵∠A=60°,∴∠AFD=30°.∴AF=2AD=8-4r.∴FC=4-(8-4r)=4r-4.
在Rt△CEF中,
∵∠C=60°,∴∠CEF=30°.∴EC=2FC.
∴4-r=2(4r-4),解得r=.∴⊙O的半径是.
24.解:(1)把A(1,0),B(-3,0)的坐标代入y=-x2+bx+c,
得解得
(2)存在.作PD∥y轴交BC于D,设直线BC的表达式为y=mx+n.
由(1)易知C(0,3).
把点B(-3,0),C(0,3)的坐标分别代入y=mx+n,
得解得
故直线BC的表达式为y=x+3,
设点P的坐标为(x,-x2-2x+3)(-3<x<0),则点D的坐标为(x,x+3),
∴PD=-x2-2x+3-(x+3)=-x2-3x,
∴S△BPC=S△PBD+S△CPD=×3×(-x2-3x)=-x2-x=-+,
当x=-时,△BPC的面积最大,此时S△BPC=,
把x=-代入y=-x2-2x+3,得y=,∴点P的坐标为.
(3)∵OB=OC=3,
∴△OBC为等腰直角三角形,∴∠OBC=∠OCB=45°.
∵BF⊥BE,∴∠FBO=45°,∴∠OEF=∠OBF=45°,∠OFE=∠OBE=45°,
∴△OEF为等腰直角三角形,∴OE=OF,∠EOF=90°,
∴S△OEF=OE·OF=OE2,
∴当OE最小时,△OEF的面积取得最小值.
∵点E在线段BC上,
∴当OE⊥BC时,OE最小,此时点E是BC的中点,∴E.
同课章节目录
