2.3 相反数 同步课件(共22张PPT)
文档属性
| 名称 | 2.3 相反数 同步课件(共22张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 00:00:00 | ||
图片预览








文档简介
人教版 初中数学
2.3 相反数
学习目标
1.借助数轴理解相反数的概念,了解互为相反数的 点在数轴上的位置关系.
2.能求出一个有理数的相反数.
3.会运用有理数相反数的意义简化多重符号.
(1) 如果规定向东为正,那么,某人向东走1.5km记作 ,向西走1.5km米记作 。
(2)如果规定零上的温度为正,某地白天的温度为零上5度,记作 ,夜间的温度为零下5度,记作 。
(3)如果规定收入为正,那么,某学生利用暑假期间打工收入400元,记作 ,开学后用这笔钱交学费400元,记作 。
+1.5km
—1.5km
+5度
— 5度
— 400元
+400元
一、温故知新,导入新课
二、看一看,辨异同
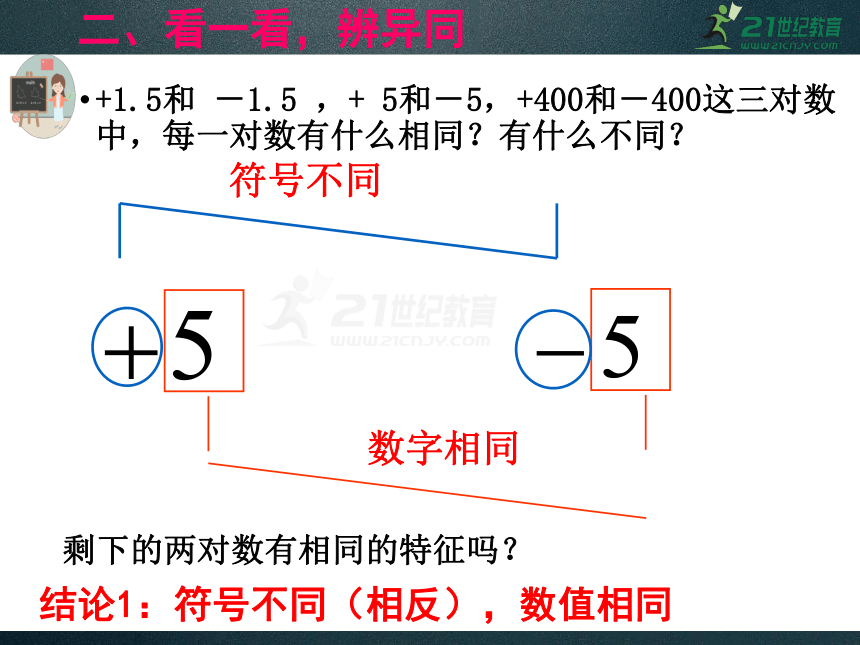
+1.5和 -1.5 ,+ 5和-5,+400和-400这三对数中,每一对数有什么相同?有什么不同?
结论1:符号不同(相反),数值相同
剩下的两对数有相同的特征吗?
数字相同
符号不同
在数轴上,画出表示以下三对数的点:(1)+1 和 -1 (2)+5 和 -5
(3)+2.5 和-2.5
这三对点,各有哪些相同?哪些不同?
- 5 -4 -3 -2 -1
0
1 2 3 4 5
+1
-1
+5
-5
+2.5
-2.5
三、想一想,找规律
结论2:每对数所对应的两点 分别在原点的两侧,到原点的距离相等。
四、相反数定义
说明:
(1)相反数是相对而言的,是成对出现的.即6是-6的
相反数,-6也是6的相反数.
(2)数形特征:符号不同(相反),数字相同
(3)几何意义:
在数轴上表示互为相反数的两数的对应点分别位于原点的两旁,且与原点的距离相等。
规定:零的相反数是零.
像-6和+6 ,-1.5和1.5这样,只有符号不同的两个数互为相反数。
例如:1.5和-1.5互为相反数,称1.5是-1.5的相反数吗,-1.5是1.5的相反数。
(4)任何一个有理数,都只有一个相反数.
(5)“只有”指的是除符号不同外,其他完全相同.
(6)相反数与前面所学的“相反意义的量”是不同的
概念.
2. 易错警示:
“只有正负号不同”不要错误地理解为
“只要正负号不同”,“只有正负号不同”包含两
层意义:(1)符号相反;(2)所含的数字相同.
例1.分别写出下列各数的相反数:
+5, - , -7 , 11.2
解:5的相反数是-5.
-7的相反数是7.
+11.2的相反数是-11.2
- 的相反数是+ .
提问:总结一下,怎样求一个有理数的相反数?
-(11.2)=-11.2
-(- )=+
-(+5)=-5
-(-7 )=+7
例题精析
1. 相反数的求法:求一个数的相反数就是在这个数
的前面加上“-”号,即a的相反数是-a,其实
质是改变这个数的符号.
要点精析:
(1)正数的相反数就是在原数前面加上“-”号;
(2)负数的相反数就是将原数前面的“-”号去掉;
(3)0的相反数是0.
相 反 数 性 质
2. 相反数的性质:若a、b互为相反数,则a+b=0
(a=-b,b=-a);反过来,若a+b=0,则a、
b互为相反数.即:
a、b互为相反数
3. 易错警示:
(1)a的相反数是-a,但-a不一定是负数.
(2)求一个式子的相反数,一定要将整个式子加
上括号,再在括号前面添上“-”号.
a+b=0.
判断题:
(1)-5是5的相反数( );
(2)-5是相反数( );
(3) 与 互为相反数( );
(4)-5和5互为相反数( ).
(5) 相反数等于它本身的数只有0 ﹙ ﹚
(6) 符号不同的两个数互为相反数﹙ ﹚
×
√
×
√
√
×
练一练
注意:
在一个数前面添上“+”号,表示这个数本身.
例如,+ (-4)=-4,+(+12)=12
当然这个“+”号必要时可以省略。
例 2.化简下列各式
(1) –(+10) (2) + (–0.15)
(3) + (+3 ) (4) –(–20 )
解: (1) –(+10)=-10 (2) + (–0.15)=-0.15
(3) +(+3)= 3 (4) –(–20)=20
化简方法:
1.正号可省略不写.
2.负负得正,两个“–”号变为“+”号。
1. 分别说出下列数的相反数。
+11.2 0 -3 -3.6 +9 -a
四、巩固练习,初步运用
-11.2
0
+3
+3.6
-9
+a
2、判断改错:
(1) 符号不同的两个数叫做相反数。 ( )
(2) 零的相反数是它本身。 ( )
(3) 一个数的相反数一定是负数。 ( )
(4) -8是相反数。 ( )
3.有的同学说:一个数的相反数一定小于它本身.你认同她的说法吗?
议一议
解:这种说法不对。
正数的相反数为负数,小于它本身;
负数的相反数为正数,大于它本身;
零的相反数是零,等于它本身。
5、写出下列各数的相反数
2
5
-
2
11
100
0
6 -8
五、分层练习,形成能力
4、如果a = - a , 那么表示a的点在数轴上的什么位置?
解:a点在原点位置。因为a = - a,说明这个数和它的相反数相等,这个数只能是0。
解:6 的相反数是-6;
-8 的相反数是8;
6.说明下列式子的意义,并且简化符号。
(7) - (-(-a)) (8) -(+(-(+a)))
(5) -(-(-2)) (6) - (-(+3))
(3) + ( + 3 ) (4) -(-20)
(1) -(+10 ) (2) -(+0.5)
(-10)
(3)
(-2)
(-a)
(-0.5)
(20)
(3)
(a)
的相反数是-
-
的相反数是
100的相反数是-100
0的相反数是0
7.(1)如果数轴上的两点A , B所表示的数互为
相反数,点A在原点的左侧,并且A,B
之间的距离是8 ,那么点B 所表示 的数
是 。
(2) 若a = -72时,则-a = 。
若-x = - 63时,则 x = 。
(3) 若a + 4 = 0 , 则 a = 。
4
72
63
-4
1.下列叙述正确的是( )
A、符号不同的两个数是互为相反数
B、一个有理数的相反数一定是负有理数
C、 与2.75都是 的相反数
D、0没有相反数
2.填空:
(1)-1.6是______的相反数,______的相反数是 .
(2) 与______互为相反数, 与______互为倒数.
(3)如果a=-a,则表示a的点在数轴的________.(什么位置)
(4)如果a=-13,那么-a=________.
(5)如果-a=-5.4,那么a=________.
(6)如果-x=9,那么x=________.
课堂测试
3.在数轴上标出2、-4.5、0各数与它们的相反数.
4.化简下列各数:
(1)-(-68);(2)-(+0.75);
(3)-(- );(4)+(+50);
5.已知4-m与-1互为相反数,求m的值.
小结:谈谈你对相反数的认识.
相反数
相反数的代数意义
相反数的几何意义
相反数的表示方法
相反数的意义
相反数的应用——利用相反数化简 双重负号
六.课堂小结
七.作业布置
教材P45 习题2.3 1,2
https://www.21cnjy.com/help/help_extract.php
2.3 相反数
学习目标
1.借助数轴理解相反数的概念,了解互为相反数的 点在数轴上的位置关系.
2.能求出一个有理数的相反数.
3.会运用有理数相反数的意义简化多重符号.
(1) 如果规定向东为正,那么,某人向东走1.5km记作 ,向西走1.5km米记作 。
(2)如果规定零上的温度为正,某地白天的温度为零上5度,记作 ,夜间的温度为零下5度,记作 。
(3)如果规定收入为正,那么,某学生利用暑假期间打工收入400元,记作 ,开学后用这笔钱交学费400元,记作 。
+1.5km
—1.5km
+5度
— 5度
— 400元
+400元
一、温故知新,导入新课
二、看一看,辨异同
+1.5和 -1.5 ,+ 5和-5,+400和-400这三对数中,每一对数有什么相同?有什么不同?
结论1:符号不同(相反),数值相同
剩下的两对数有相同的特征吗?
数字相同
符号不同
在数轴上,画出表示以下三对数的点:(1)+1 和 -1 (2)+5 和 -5
(3)+2.5 和-2.5
这三对点,各有哪些相同?哪些不同?
- 5 -4 -3 -2 -1
0
1 2 3 4 5
+1
-1
+5
-5
+2.5
-2.5
三、想一想,找规律
结论2:每对数所对应的两点 分别在原点的两侧,到原点的距离相等。
四、相反数定义
说明:
(1)相反数是相对而言的,是成对出现的.即6是-6的
相反数,-6也是6的相反数.
(2)数形特征:符号不同(相反),数字相同
(3)几何意义:
在数轴上表示互为相反数的两数的对应点分别位于原点的两旁,且与原点的距离相等。
规定:零的相反数是零.
像-6和+6 ,-1.5和1.5这样,只有符号不同的两个数互为相反数。
例如:1.5和-1.5互为相反数,称1.5是-1.5的相反数吗,-1.5是1.5的相反数。
(4)任何一个有理数,都只有一个相反数.
(5)“只有”指的是除符号不同外,其他完全相同.
(6)相反数与前面所学的“相反意义的量”是不同的
概念.
2. 易错警示:
“只有正负号不同”不要错误地理解为
“只要正负号不同”,“只有正负号不同”包含两
层意义:(1)符号相反;(2)所含的数字相同.
例1.分别写出下列各数的相反数:
+5, - , -7 , 11.2
解:5的相反数是-5.
-7的相反数是7.
+11.2的相反数是-11.2
- 的相反数是+ .
提问:总结一下,怎样求一个有理数的相反数?
-(11.2)=-11.2
-(- )=+
-(+5)=-5
-(-7 )=+7
例题精析
1. 相反数的求法:求一个数的相反数就是在这个数
的前面加上“-”号,即a的相反数是-a,其实
质是改变这个数的符号.
要点精析:
(1)正数的相反数就是在原数前面加上“-”号;
(2)负数的相反数就是将原数前面的“-”号去掉;
(3)0的相反数是0.
相 反 数 性 质
2. 相反数的性质:若a、b互为相反数,则a+b=0
(a=-b,b=-a);反过来,若a+b=0,则a、
b互为相反数.即:
a、b互为相反数
3. 易错警示:
(1)a的相反数是-a,但-a不一定是负数.
(2)求一个式子的相反数,一定要将整个式子加
上括号,再在括号前面添上“-”号.
a+b=0.
判断题:
(1)-5是5的相反数( );
(2)-5是相反数( );
(3) 与 互为相反数( );
(4)-5和5互为相反数( ).
(5) 相反数等于它本身的数只有0 ﹙ ﹚
(6) 符号不同的两个数互为相反数﹙ ﹚
×
√
×
√
√
×
练一练
注意:
在一个数前面添上“+”号,表示这个数本身.
例如,+ (-4)=-4,+(+12)=12
当然这个“+”号必要时可以省略。
例 2.化简下列各式
(1) –(+10) (2) + (–0.15)
(3) + (+3 ) (4) –(–20 )
解: (1) –(+10)=-10 (2) + (–0.15)=-0.15
(3) +(+3)= 3 (4) –(–20)=20
化简方法:
1.正号可省略不写.
2.负负得正,两个“–”号变为“+”号。
1. 分别说出下列数的相反数。
+11.2 0 -3 -3.6 +9 -a
四、巩固练习,初步运用
-11.2
0
+3
+3.6
-9
+a
2、判断改错:
(1) 符号不同的两个数叫做相反数。 ( )
(2) 零的相反数是它本身。 ( )
(3) 一个数的相反数一定是负数。 ( )
(4) -8是相反数。 ( )
3.有的同学说:一个数的相反数一定小于它本身.你认同她的说法吗?
议一议
解:这种说法不对。
正数的相反数为负数,小于它本身;
负数的相反数为正数,大于它本身;
零的相反数是零,等于它本身。
5、写出下列各数的相反数
2
5
-
2
11
100
0
6 -8
五、分层练习,形成能力
4、如果a = - a , 那么表示a的点在数轴上的什么位置?
解:a点在原点位置。因为a = - a,说明这个数和它的相反数相等,这个数只能是0。
解:6 的相反数是-6;
-8 的相反数是8;
6.说明下列式子的意义,并且简化符号。
(7) - (-(-a)) (8) -(+(-(+a)))
(5) -(-(-2)) (6) - (-(+3))
(3) + ( + 3 ) (4) -(-20)
(1) -(+10 ) (2) -(+0.5)
(-10)
(3)
(-2)
(-a)
(-0.5)
(20)
(3)
(a)
的相反数是-
-
的相反数是
100的相反数是-100
0的相反数是0
7.(1)如果数轴上的两点A , B所表示的数互为
相反数,点A在原点的左侧,并且A,B
之间的距离是8 ,那么点B 所表示 的数
是 。
(2) 若a = -72时,则-a = 。
若-x = - 63时,则 x = 。
(3) 若a + 4 = 0 , 则 a = 。
4
72
63
-4
1.下列叙述正确的是( )
A、符号不同的两个数是互为相反数
B、一个有理数的相反数一定是负有理数
C、 与2.75都是 的相反数
D、0没有相反数
2.填空:
(1)-1.6是______的相反数,______的相反数是 .
(2) 与______互为相反数, 与______互为倒数.
(3)如果a=-a,则表示a的点在数轴的________.(什么位置)
(4)如果a=-13,那么-a=________.
(5)如果-a=-5.4,那么a=________.
(6)如果-x=9,那么x=________.
课堂测试
3.在数轴上标出2、-4.5、0各数与它们的相反数.
4.化简下列各数:
(1)-(-68);(2)-(+0.75);
(3)-(- );(4)+(+50);
5.已知4-m与-1互为相反数,求m的值.
小结:谈谈你对相反数的认识.
相反数
相反数的代数意义
相反数的几何意义
相反数的表示方法
相反数的意义
相反数的应用——利用相反数化简 双重负号
六.课堂小结
七.作业布置
教材P45 习题2.3 1,2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
