青岛版八年级上 第一章轴对称与轴对称图形预习学案
文档属性
| 名称 | 青岛版八年级上 第一章轴对称与轴对称图形预习学案 |  | |
| 格式 | zip | ||
| 文件大小 | 40.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-18 21:29:23 | ||
图片预览



文档简介
预习课题: 八年级上册 第一章:轴对称与轴对称图形
第一节:我们身边的轴对称图形 (一课时)
预习目标:
1、理解在丰富的现实情景中,观察生活中的轴对称现象,探索轴对称图形的共同特征,经历现实世界中抽象出轴对称概念的活动。
2 通过对折的方法认识轴对称图形,能指出轴对称图形的对称轴和对称点。
3 通过丰富的生活实例,经历抽象出两个图形关于一条直线成轴对称的概念过程,能够识别对称轴与对称点,并能说出“轴对称图形”和“两个图形关于一条直线成轴对称”的区别和联系。
预习重点:轴对称图形的共同特征。
预习任务:
1、预习要求:预习教材P4—P6页,结合教材的轴对称图形,体会轴对称图形的特点。
2、预习活动:按教材要求自己动手折叠一张长方形的纸。
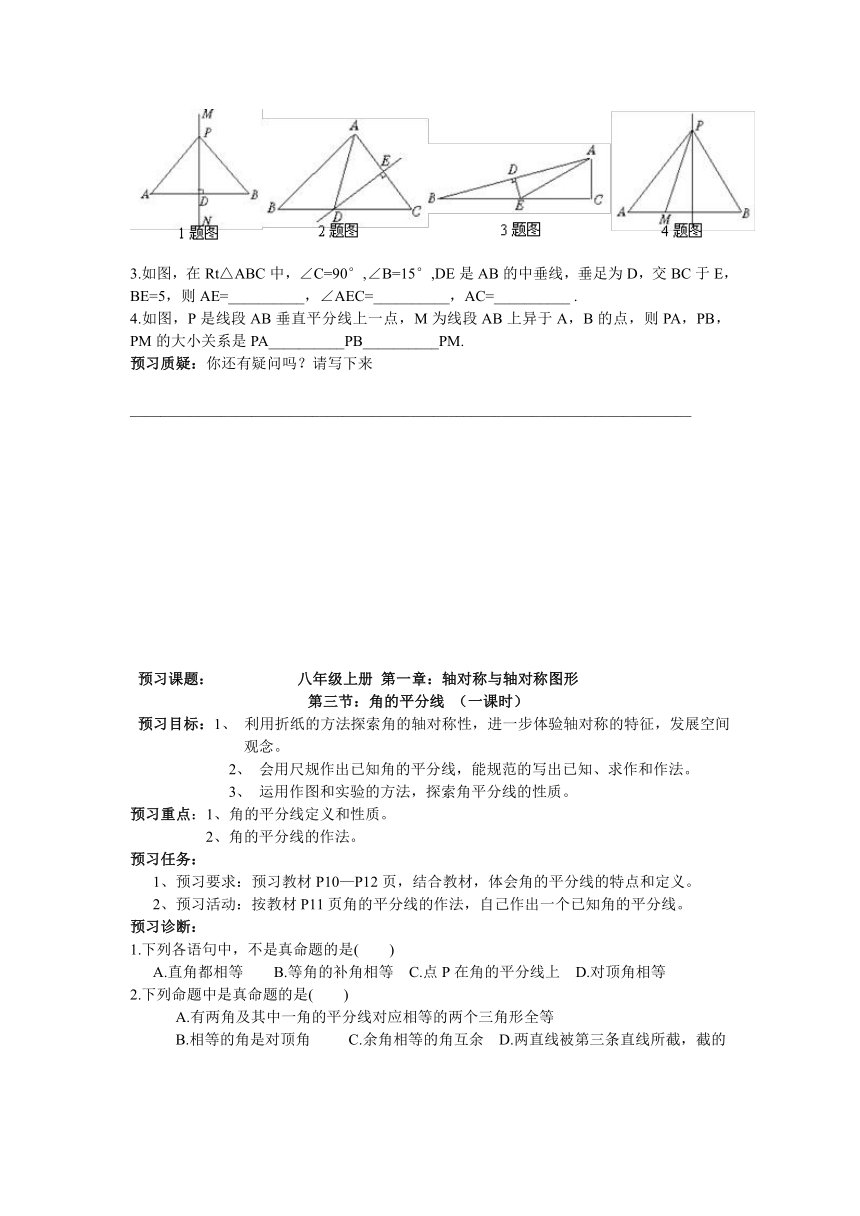
3、写出图2中的对称点;画出下面图形中的对称轴
4、下面的字母、数字、汉字那些是轴对称图形?它们各有几条对称轴?
A C D E F T G H U
1 2 3 4 5 6 7 8 9
王 上 田 大 中 日 人 朋 两
5、请同学们搜集一些生活中的轴对称图形,看谁搜集的多、准?
预习诊断:
一.填空。
1.如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是( ),折痕所在的直线叫做( )。
2.圆的对称轴有( )条,半圆形的对称轴有( )条。
3.在对称图形中,对称轴两侧相对的点到对称轴的( )。
4.( )三角形有三条对称轴,( )三角形有一条对称轴。
5.正方形有( )条对称轴,长方形有( )条对称轴,等腰梯形有( )条对称轴。
二.判断。
1.通过一个圆的圆心的直线是这个圆的对称轴。 ( )
2.圆是轴对称图形,每一条直径都是它的对称轴。( )
3.等腰梯形是对称图形。 ( )
4.正方形只有一条对称轴。 ( )
三.选择。
1.下列图形中,对称轴最多的是( )。
① 等边三角形 ② 正方形 ③ 圆 ④ 长方
预习质疑:你还有疑问吗?请写下来
__________________________________________________________________________
预习课题: 八年级上册 第一章:轴对称与轴对称图形
第二节:线段的垂直平分线 (一课时)
预习目标:1、 经历线段的垂直平分线概念的形成过程,认识线段的轴对称性,进一步体验轴对称的特征,发展空间观念。
2、 会用尺规作出已知线段的垂直平分线,能规范的写出已知、求作和作法。
3、 运用作图和实验的方法,探索线段的垂直平分线的性质。
预习重点:1、线段的垂直平分线的定义和性质。
2、线段的垂直平分线的作法。
预习任务:
1、预习要求:预习教材P8—P9页,结合教材,体会线段的垂直平分线的特点和定义。
2、预习活动:按教材P9页线段的垂直平分线的作法,自己作出一条线段的线段的垂直平分线。
3、下图中的线段AB的垂直平分线是 图中相等的线段有
4、(1)下图中的线段AB的垂直平分线是 图中相等的线段有
(2)在直线DE上任找一点P,连接PA、PB则PA、PB的有怎样的关系?
预习诊断:
1.如图,已知直线MN是线段AB的垂直平分线,垂足为D,点P是MN上一点,若AB=10 cm,则BD=__________cm;若PA=10 cm,则PB=__________cm;此时,PD=__________cm.
2.如图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长是12 cm,AC=5cm,则AB+BD+AD=________cm;AB+BD+DC=__________cm;△ABC的周长是__________cm.
3.如图,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的中垂线,垂足为D,交BC于E,BE=5,则AE=__________,∠AEC=__________,AC=__________ .
4.如图,P是线段AB垂直平分线上一点,M为线段AB上异于A,B的点,则PA,PB,PM的大小关系是PA__________PB__________PM.
预习质疑:你还有疑问吗?请写下来
__________________________________________________________________________
预习课题: 八年级上册 第一章:轴对称与轴对称图形
第三节:角的平分线 (一课时)
预习目标:1、 利用折纸的方法探索角的轴对称性,进一步体验轴对称的特征,发展空间观念。
2、 会用尺规作出已知角的平分线,能规范的写出已知、求作和作法。
3、 运用作图和实验的方法,探索角平分线的性质。
预习重点:1、角的平分线定义和性质。
2、角的平分线的作法。
预习任务:
1、预习要求:预习教材P10—P12页,结合教材,体会角的平分线的特点和定义。
2、预习活动:按教材P11页角的平分线的作法,自己作出一个已知角的平分线。
预习诊断:
1.下列各语句中,不是真命题的是( )
A.直角都相等 B.等角的补角相等 C.点P在角的平分线上 D.对顶角相等
2.下列命题中是真命题的是( )
A.有两角及其中一角的平分线对应相等的两个三角形全等
B.相等的角是对顶角 C.余角相等的角互余 D.两直线被第三条直线所截,截的
同角相等
3.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D, 如果AC=3 cm,那么AE+DE等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
4.如图,已知AB=AC,AE=AF,BE与CF交于点D,则
①△ABE≌△ACF ②△BDF≌△CDE ③D在∠BAC的平分线上,以上结论中,正确的是( )
A.只有① B.只有② C.只有①和② D.①,②与③
5.给出下列结论,正确的有( )
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个 B.2个 C.3个 D.4个
6.(1)利用角平分线的性质,找到△ABC(背面自画任意△)内部距三边距离相等的点.
(2)在上图△ABC所在平面中,找到距三边所在直线距离相等的点.
7.如图5,已知OE、OD分别平分∠AOB和∠BOC,若∠AOB=90°,
∠EOD=70°,求∠BOC的度数.
预习质疑:你还有疑问吗?请写下来
__________________________________________________________________________
预习课题:八年级上册 第一章:轴对称与轴对称图形
第四节等腰三角形 第1课时
预习目标:1.经历探索等腰三角形的性质的过程,掌握等腰三角形的轴对称性、等腰三角形的“三线合一”、 等腰三角形的两个底角相等的性质。
2.经历探索等边三角形的轴对称性和内角相等性质的过程,掌握并会作出合理的解释。
预习重点:对性质的理解和应用。
预习内容:
预习交流:
任务一: 预习课本P13,完成课本六个问题,得出:
性质1: 等腰三角形的轴对称性
等腰三角形是轴对称图形,对称轴是( )。
性质2::等腰三角形的两个底角相等。(等边对等角)
如图,(课本P13图)
∵AB=AC
∴∠( )=∠( )
性质3: 等.腰三角形的“三线合一”性质
等腰三角形的( )、( )、( )重合。
预习诊断:
如右图,(课本P13图)填空:
∵AB=AC,∠1=∠2,
∴( )=( ) ,( )⊥( )
∵AB=AC,AD⊥BC,
∴∠( )=∠( ),( )=( )
∵AB=AC,BD=DC,
∴∠( )=∠( ),( )⊥( )
任务二: 等边三角形的性质
预习课本P14,完成“交流与发现”的问题,得出:
等边三角形是轴对称图形,它有( )条对称轴。
等边三角形的三个内角都( )。
预习诊断:如图,△ABC是等边三角形,AE⊥BC于E,则下列结论中正确的个数是( )
(1) AB=AC=BC (2)∠BAC=∠B=∠C (3) AE是∠BAC 的平分线 (4) AE是△ABC的对称轴
A. 1 B. 2 C . 3 D. 4
预习质疑:
课堂实施:
(一)展示交流:
.以小组为单位交流预习题目中的各个问题,并找出各自的疑难问题,共同解决疑难问题。
(二)反思创新:.已知房屋的顶角∠BAC=1000,过屋顶A的立柱AD⊥BC于D,屋椽AB=AC,求顶架上∠B,∠C、∠BAD、∠CAD的度数。
(三)系统总结:本节学习了哪些知识?
限时作业:
(1)已知等腰三角形有一个内角为700,求其它两个内角的度数。
(2)已知等腰三角形有一个内角为1100,求其它两个内角的度数。
预习课题:八年级上册 第一章:轴对称与轴对称图形
第四节等腰三角形 第2课时
预习目标:掌握已知底边和底边上的高,用尺规作等腰三角形的方法
预习重点:用尺规作等腰三角形
预习内容:任务一 : 已知等腰三角形底边与底边上的高作等腰三角形
预习课本P15,完成下列问题
根据下面所写的已知、求作,填写作法并作出图形
已知:线段a,h,求作:△ABC,使AC=BC,AB=a, 底边上的高CD=h
作法:(1)作线段AB,使AB=______.
(2)作线段AB的___________EF,交AB于点D
(3)在射线DE上截取线段DC,使DC=h
(4)连接( )、( )
△ABC就是( )
预习诊断:①为什么这样画出的三角形是等腰三角形?
②已知:C、D是∠AOB内的两点,
求作:点P,使P到∠AOB两边的距离相等,并且到点C和D的距离也相等
任务二 : 等腰三角形的识别
方法:(1)定义:___________相等的三角形叫等腰三角形。
(2)如果一个三角形有_________相等,那么这两个角所对的边也相等(简写成“等角对等边”)
(3)如果一个三角形一边上的高、中线和这条边所对的角平分线有任意两条线互相重合,那么这个三角形是等腰三角形。
预习诊断:△ABC 中,∠A=360,∠C=720,∠DBC=360,试找出图中所有等腰三角形,并说明理由。
任务三: 等边三角形的识别
①______________都相等的三角形是等边三角形。
②______________都相等的三角形是等边三角形。
预习诊断:如图(课本P16第2题图),在方格纸上有一个△ABC,它是什么形状的三角形?简要说明理由。
预习质疑:
课堂实施:
展示交流:
(二) 反思拓展:
如图(课本P16第4题图),在△ABC中,∠DAC是三角形的一个外角,AE平分∠DAC,AE∥BC,问△ABC是等腰三角形吗?说明你的理由。
(三) 系统总结:本节学习了哪些知识?
限时作业:
已知线段a,s ( s>2a ),求作等腰三角形,
使它的底边等于a,周长等于s.
如图(课本P16第4题图),在△ABC中,AB=AC,∠DAC是三角形的一个外角,AE平分∠DAC,问AE与BC平行吗?为什么?
3.已知在△ABC中,AB=AC,D、E分别是BC边上的点,并且AD=AE,试说明BD=CE
数学八年级上册第一章第五节成轴对称的图形的性质第1课时
预习目标:
动手操作,经历探索轴对称的图形的过程,总结成轴对称的图形的性质
理解连接对应点的线段被对称轴平分,对应线段相等,对应角相等的性质。
预习重点:成轴对称的图形的性质
预习任务:
认真阅读课本17页的实验与探究并回答提出的3个问题。你能总结成轴对称的图形的性质吗?
阅读例1并尝试完成练习1.2题。
预习诊断:
1.如果两个图形关于一条直线成轴对称,那么连接对应点的线段被对称轴 ,对应线段------,对应角------。
2.将一个等腰三角形对折后剪开平移,试指出图中对应点,对应线段,对应角。
预习质疑:
数学八年级上册第一章第五节成轴对称的图形的性质第2课时
预习目标:
理解连接对应点的线段被对称轴平分,对应线段相等,对应角相等的性质。
会画出与已知图形关于某直线对称的图形。
预习重点:与已知图形关于某直线对称的图形的图形的画法。
预习任务:
1.认真阅读课本18页的交流与发现并思考怎样画已知点的对称点。
2.阅读例2并尝试完成练习1.2题。
预习诊断:
1. 画已知点关于某直线的对称点,只需过这个点作这条直线的
并延长,使延长的部分等于所作的 。
2.完成教材20页习题第5题。
预习质疑:
数学八年级上册第一章第六节镜面对称
预习目标:
结合现实生活中的实例,认识镜面对称及其应用,感受镜面对称。
发现镜面对称下图形的变化。
预习重点:镜面对称下图形的变化。
预习任务:
1.认真阅读课本21--23页的内容,并联系现实生活中的实例总结镜面对称的变化规律。
2. 感受镜面对称的数学美,并能说出镜面对称在现实生活中的应用。
3.完成24页练习1.2题。
预习诊断:
镜面对称的------、------相同,但左右位置不同的两个点的位置恰好--------。
尝试做24页习题1.2题。
预习质疑:
数学八年级上册第一章第七节简单的图案设计
预习目标:
发现生活中的轴对称图形,并能分析它是由哪些简单几何图形组成的。
能利用简单几何图形设计轴对称图案,体验数学活动的乐趣和数学美。
预习重点:利用简单几何图形设计轴对称图案。
预习任务:
1.认真阅读课本25--26页的内容并回答提出的问题,联系现实生活中的实例总结轴对称图案的设计规律。
2.完成26页练习1题。
预习诊断:
说出你身边的轴对称的图案。
2.完成26页艺术节徽标设计图案
尝试做24页习题1.2题。
预习质疑:
第一节:我们身边的轴对称图形 (一课时)
预习目标:
1、理解在丰富的现实情景中,观察生活中的轴对称现象,探索轴对称图形的共同特征,经历现实世界中抽象出轴对称概念的活动。
2 通过对折的方法认识轴对称图形,能指出轴对称图形的对称轴和对称点。
3 通过丰富的生活实例,经历抽象出两个图形关于一条直线成轴对称的概念过程,能够识别对称轴与对称点,并能说出“轴对称图形”和“两个图形关于一条直线成轴对称”的区别和联系。
预习重点:轴对称图形的共同特征。
预习任务:
1、预习要求:预习教材P4—P6页,结合教材的轴对称图形,体会轴对称图形的特点。
2、预习活动:按教材要求自己动手折叠一张长方形的纸。
3、写出图2中的对称点;画出下面图形中的对称轴
4、下面的字母、数字、汉字那些是轴对称图形?它们各有几条对称轴?
A C D E F T G H U
1 2 3 4 5 6 7 8 9
王 上 田 大 中 日 人 朋 两
5、请同学们搜集一些生活中的轴对称图形,看谁搜集的多、准?
预习诊断:
一.填空。
1.如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是( ),折痕所在的直线叫做( )。
2.圆的对称轴有( )条,半圆形的对称轴有( )条。
3.在对称图形中,对称轴两侧相对的点到对称轴的( )。
4.( )三角形有三条对称轴,( )三角形有一条对称轴。
5.正方形有( )条对称轴,长方形有( )条对称轴,等腰梯形有( )条对称轴。
二.判断。
1.通过一个圆的圆心的直线是这个圆的对称轴。 ( )
2.圆是轴对称图形,每一条直径都是它的对称轴。( )
3.等腰梯形是对称图形。 ( )
4.正方形只有一条对称轴。 ( )
三.选择。
1.下列图形中,对称轴最多的是( )。
① 等边三角形 ② 正方形 ③ 圆 ④ 长方
预习质疑:你还有疑问吗?请写下来
__________________________________________________________________________
预习课题: 八年级上册 第一章:轴对称与轴对称图形
第二节:线段的垂直平分线 (一课时)
预习目标:1、 经历线段的垂直平分线概念的形成过程,认识线段的轴对称性,进一步体验轴对称的特征,发展空间观念。
2、 会用尺规作出已知线段的垂直平分线,能规范的写出已知、求作和作法。
3、 运用作图和实验的方法,探索线段的垂直平分线的性质。
预习重点:1、线段的垂直平分线的定义和性质。
2、线段的垂直平分线的作法。
预习任务:
1、预习要求:预习教材P8—P9页,结合教材,体会线段的垂直平分线的特点和定义。
2、预习活动:按教材P9页线段的垂直平分线的作法,自己作出一条线段的线段的垂直平分线。
3、下图中的线段AB的垂直平分线是 图中相等的线段有
4、(1)下图中的线段AB的垂直平分线是 图中相等的线段有
(2)在直线DE上任找一点P,连接PA、PB则PA、PB的有怎样的关系?
预习诊断:
1.如图,已知直线MN是线段AB的垂直平分线,垂足为D,点P是MN上一点,若AB=10 cm,则BD=__________cm;若PA=10 cm,则PB=__________cm;此时,PD=__________cm.
2.如图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长是12 cm,AC=5cm,则AB+BD+AD=________cm;AB+BD+DC=__________cm;△ABC的周长是__________cm.
3.如图,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的中垂线,垂足为D,交BC于E,BE=5,则AE=__________,∠AEC=__________,AC=__________ .
4.如图,P是线段AB垂直平分线上一点,M为线段AB上异于A,B的点,则PA,PB,PM的大小关系是PA__________PB__________PM.
预习质疑:你还有疑问吗?请写下来
__________________________________________________________________________
预习课题: 八年级上册 第一章:轴对称与轴对称图形
第三节:角的平分线 (一课时)
预习目标:1、 利用折纸的方法探索角的轴对称性,进一步体验轴对称的特征,发展空间观念。
2、 会用尺规作出已知角的平分线,能规范的写出已知、求作和作法。
3、 运用作图和实验的方法,探索角平分线的性质。
预习重点:1、角的平分线定义和性质。
2、角的平分线的作法。
预习任务:
1、预习要求:预习教材P10—P12页,结合教材,体会角的平分线的特点和定义。
2、预习活动:按教材P11页角的平分线的作法,自己作出一个已知角的平分线。
预习诊断:
1.下列各语句中,不是真命题的是( )
A.直角都相等 B.等角的补角相等 C.点P在角的平分线上 D.对顶角相等
2.下列命题中是真命题的是( )
A.有两角及其中一角的平分线对应相等的两个三角形全等
B.相等的角是对顶角 C.余角相等的角互余 D.两直线被第三条直线所截,截的
同角相等
3.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D, 如果AC=3 cm,那么AE+DE等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
4.如图,已知AB=AC,AE=AF,BE与CF交于点D,则
①△ABE≌△ACF ②△BDF≌△CDE ③D在∠BAC的平分线上,以上结论中,正确的是( )
A.只有① B.只有② C.只有①和② D.①,②与③
5.给出下列结论,正确的有( )
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个 B.2个 C.3个 D.4个
6.(1)利用角平分线的性质,找到△ABC(背面自画任意△)内部距三边距离相等的点.
(2)在上图△ABC所在平面中,找到距三边所在直线距离相等的点.
7.如图5,已知OE、OD分别平分∠AOB和∠BOC,若∠AOB=90°,
∠EOD=70°,求∠BOC的度数.
预习质疑:你还有疑问吗?请写下来
__________________________________________________________________________
预习课题:八年级上册 第一章:轴对称与轴对称图形
第四节等腰三角形 第1课时
预习目标:1.经历探索等腰三角形的性质的过程,掌握等腰三角形的轴对称性、等腰三角形的“三线合一”、 等腰三角形的两个底角相等的性质。
2.经历探索等边三角形的轴对称性和内角相等性质的过程,掌握并会作出合理的解释。
预习重点:对性质的理解和应用。
预习内容:
预习交流:
任务一: 预习课本P13,完成课本六个问题,得出:
性质1: 等腰三角形的轴对称性
等腰三角形是轴对称图形,对称轴是( )。
性质2::等腰三角形的两个底角相等。(等边对等角)
如图,(课本P13图)
∵AB=AC
∴∠( )=∠( )
性质3: 等.腰三角形的“三线合一”性质
等腰三角形的( )、( )、( )重合。
预习诊断:
如右图,(课本P13图)填空:
∵AB=AC,∠1=∠2,
∴( )=( ) ,( )⊥( )
∵AB=AC,AD⊥BC,
∴∠( )=∠( ),( )=( )
∵AB=AC,BD=DC,
∴∠( )=∠( ),( )⊥( )
任务二: 等边三角形的性质
预习课本P14,完成“交流与发现”的问题,得出:
等边三角形是轴对称图形,它有( )条对称轴。
等边三角形的三个内角都( )。
预习诊断:如图,△ABC是等边三角形,AE⊥BC于E,则下列结论中正确的个数是( )
(1) AB=AC=BC (2)∠BAC=∠B=∠C (3) AE是∠BAC 的平分线 (4) AE是△ABC的对称轴
A. 1 B. 2 C . 3 D. 4
预习质疑:
课堂实施:
(一)展示交流:
.以小组为单位交流预习题目中的各个问题,并找出各自的疑难问题,共同解决疑难问题。
(二)反思创新:.已知房屋的顶角∠BAC=1000,过屋顶A的立柱AD⊥BC于D,屋椽AB=AC,求顶架上∠B,∠C、∠BAD、∠CAD的度数。
(三)系统总结:本节学习了哪些知识?
限时作业:
(1)已知等腰三角形有一个内角为700,求其它两个内角的度数。
(2)已知等腰三角形有一个内角为1100,求其它两个内角的度数。
预习课题:八年级上册 第一章:轴对称与轴对称图形
第四节等腰三角形 第2课时
预习目标:掌握已知底边和底边上的高,用尺规作等腰三角形的方法
预习重点:用尺规作等腰三角形
预习内容:任务一 : 已知等腰三角形底边与底边上的高作等腰三角形
预习课本P15,完成下列问题
根据下面所写的已知、求作,填写作法并作出图形
已知:线段a,h,求作:△ABC,使AC=BC,AB=a, 底边上的高CD=h
作法:(1)作线段AB,使AB=______.
(2)作线段AB的___________EF,交AB于点D
(3)在射线DE上截取线段DC,使DC=h
(4)连接( )、( )
△ABC就是( )
预习诊断:①为什么这样画出的三角形是等腰三角形?
②已知:C、D是∠AOB内的两点,
求作:点P,使P到∠AOB两边的距离相等,并且到点C和D的距离也相等
任务二 : 等腰三角形的识别
方法:(1)定义:___________相等的三角形叫等腰三角形。
(2)如果一个三角形有_________相等,那么这两个角所对的边也相等(简写成“等角对等边”)
(3)如果一个三角形一边上的高、中线和这条边所对的角平分线有任意两条线互相重合,那么这个三角形是等腰三角形。
预习诊断:△ABC 中,∠A=360,∠C=720,∠DBC=360,试找出图中所有等腰三角形,并说明理由。
任务三: 等边三角形的识别
①______________都相等的三角形是等边三角形。
②______________都相等的三角形是等边三角形。
预习诊断:如图(课本P16第2题图),在方格纸上有一个△ABC,它是什么形状的三角形?简要说明理由。
预习质疑:
课堂实施:
展示交流:
(二) 反思拓展:
如图(课本P16第4题图),在△ABC中,∠DAC是三角形的一个外角,AE平分∠DAC,AE∥BC,问△ABC是等腰三角形吗?说明你的理由。
(三) 系统总结:本节学习了哪些知识?
限时作业:
已知线段a,s ( s>2a ),求作等腰三角形,
使它的底边等于a,周长等于s.
如图(课本P16第4题图),在△ABC中,AB=AC,∠DAC是三角形的一个外角,AE平分∠DAC,问AE与BC平行吗?为什么?
3.已知在△ABC中,AB=AC,D、E分别是BC边上的点,并且AD=AE,试说明BD=CE
数学八年级上册第一章第五节成轴对称的图形的性质第1课时
预习目标:
动手操作,经历探索轴对称的图形的过程,总结成轴对称的图形的性质
理解连接对应点的线段被对称轴平分,对应线段相等,对应角相等的性质。
预习重点:成轴对称的图形的性质
预习任务:
认真阅读课本17页的实验与探究并回答提出的3个问题。你能总结成轴对称的图形的性质吗?
阅读例1并尝试完成练习1.2题。
预习诊断:
1.如果两个图形关于一条直线成轴对称,那么连接对应点的线段被对称轴 ,对应线段------,对应角------。
2.将一个等腰三角形对折后剪开平移,试指出图中对应点,对应线段,对应角。
预习质疑:
数学八年级上册第一章第五节成轴对称的图形的性质第2课时
预习目标:
理解连接对应点的线段被对称轴平分,对应线段相等,对应角相等的性质。
会画出与已知图形关于某直线对称的图形。
预习重点:与已知图形关于某直线对称的图形的图形的画法。
预习任务:
1.认真阅读课本18页的交流与发现并思考怎样画已知点的对称点。
2.阅读例2并尝试完成练习1.2题。
预习诊断:
1. 画已知点关于某直线的对称点,只需过这个点作这条直线的
并延长,使延长的部分等于所作的 。
2.完成教材20页习题第5题。
预习质疑:
数学八年级上册第一章第六节镜面对称
预习目标:
结合现实生活中的实例,认识镜面对称及其应用,感受镜面对称。
发现镜面对称下图形的变化。
预习重点:镜面对称下图形的变化。
预习任务:
1.认真阅读课本21--23页的内容,并联系现实生活中的实例总结镜面对称的变化规律。
2. 感受镜面对称的数学美,并能说出镜面对称在现实生活中的应用。
3.完成24页练习1.2题。
预习诊断:
镜面对称的------、------相同,但左右位置不同的两个点的位置恰好--------。
尝试做24页习题1.2题。
预习质疑:
数学八年级上册第一章第七节简单的图案设计
预习目标:
发现生活中的轴对称图形,并能分析它是由哪些简单几何图形组成的。
能利用简单几何图形设计轴对称图案,体验数学活动的乐趣和数学美。
预习重点:利用简单几何图形设计轴对称图案。
预习任务:
1.认真阅读课本25--26页的内容并回答提出的问题,联系现实生活中的实例总结轴对称图案的设计规律。
2.完成26页练习1题。
预习诊断:
说出你身边的轴对称的图案。
2.完成26页艺术节徽标设计图案
尝试做24页习题1.2题。
预习质疑:
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
