14.2.1作轴对称图形
文档属性
| 名称 | 14.2.1作轴对称图形 |

|
|
| 格式 | rar | ||
| 文件大小 | 737.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-18 23:37:28 | ||
图片预览









文档简介
(共35张PPT)
雨露学校 八年级数学备课组
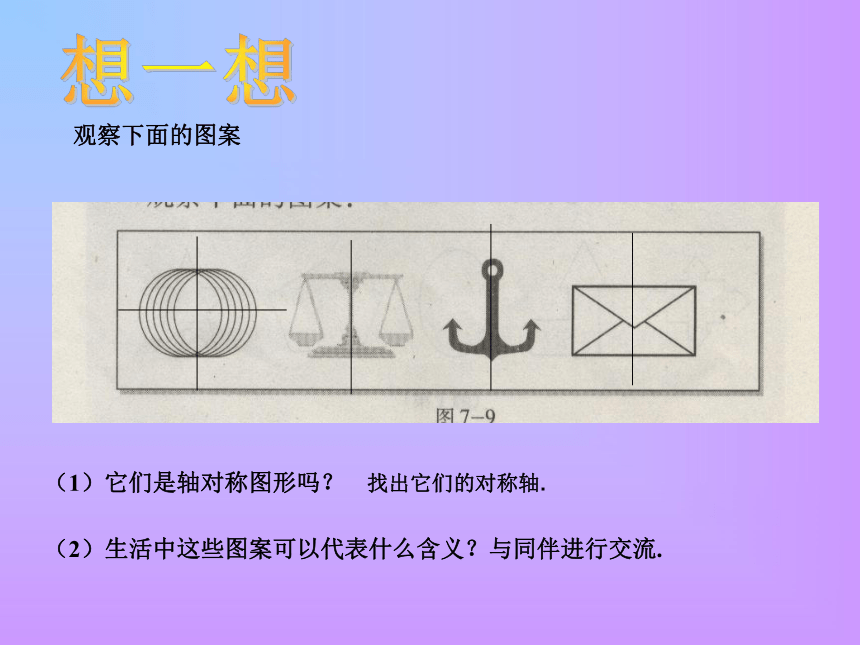
观察下面的图案
(1)它们是轴对称图形吗?
(2)生活中这些图案可以代表什么含义?与同伴进行交流.
找出它们的对称轴.
什么是轴对称图形?什么叫两个图形成轴对称?
1、如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
2、对于两个图形,如果沿一条直线对折后,它们能完全重合,那么 这两个图形成轴对称,这条直线就是对称轴.
轴对称主要有哪些性质?
1、关于某条直线对称的两个图形是全等形;
2、如果两个图形关于某直线对称,那么对应点所连的线段被对称轴垂直平分;
3、成轴对称的两个图形的对应线段相等,对应角相等.
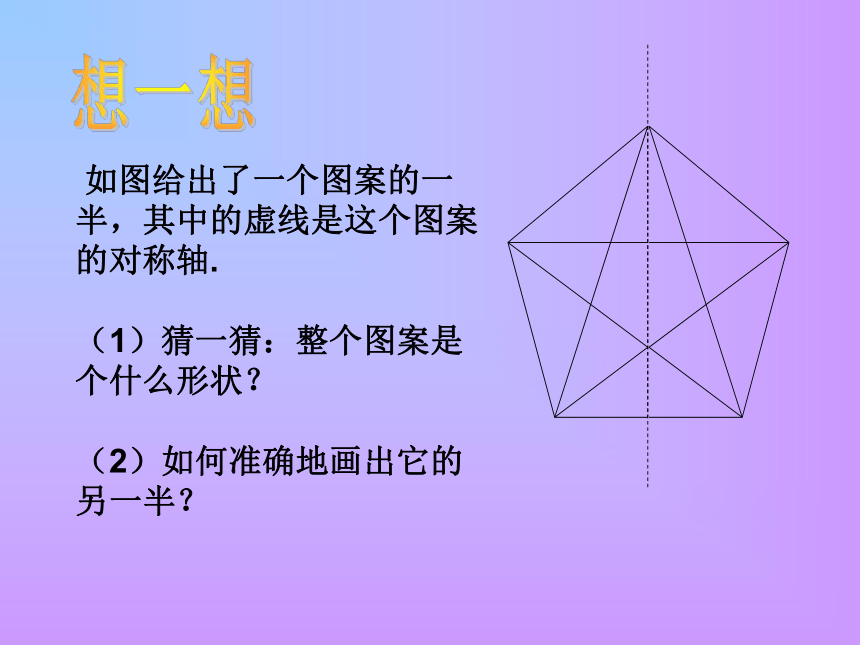
如图给出了一个图案的一半,其中的虚线是这个图案的对称轴.
(1)猜一猜:整个图案是个什么形状?
(2)如何准确地画出它的另一半?
已知对称轴 l 和一个点A如何画出点A关于 l 的对称点A’
3、点 A’ 就是点A关于 l 的对称点.
A
A’
1、过点A作对称轴 l 的垂线,垂足为B;
2、延长A B 至A’,使得BA’= A B.
B
l
1、 如何画线段AB关于直线L的
对称线段A’B’
找关键点作出其对称点!
然后连结线段.
A
B
A’
B’
B’
A’
2、如何画 ⊿ABC关于直线L的
对称⊿ A’B’C’
还是找关键点作出其对称点!
然后顺次连结线段构成三角形.
A
B
几何图形都可以看作由点组成,只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形;对于一些由直线、线段或射线组成的图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
3、如图给出了一个图案的一半,其中
的虚线 是这个图案的对称轴.
(1)整个图案是个什么形状?
(2)请准确地画出它的另一半.
仿照上面完成教科书上P41页练习1
4、请画出⊿ABC关于直线 的对称⊿ A’B’C’.
A
B
C
找关键点作出对称点!然后连结线段.
1、画出点A关于 l 的对称点A’:
( 3 )点 A’ 就是点A关于 l 的对称点.
( 1 )过点A作对称轴 l 的垂线,垂足为B;
( 2 )延长A B 至A’,使得BA’= A B.
A
A’
B
l
2、画简单平面图形的对称图形:
3、利用轴对称设计图案.
由一个平面图形得到它的轴对称的图形叫做轴对称变换。
轴对称变换
轴对称变换不会改变图形的 和
,只会改变图形 。
大小
位置
形状
下面的数据是某个时间经过轴对称变换而得来的,请问它表示的时间是多少?
利用轴对称变换以及变换后的一些特征,我们可以解决许多实际问题。
如图所示:从A地到B地有三条路可供选择,你会选择哪条路距离最短?你的理由是什么?
两点之间线段最短
如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?
P
所以泵站建在点P可使输气管线最短
如图,如果A,B在燃气管道L的同旁,泵站应修在管道的什么地方,可使所用的输气管线最短?
思考???
为什么在P点的位置修建泵站,就能使所用的管线最短呢?
总结经验:
实际上是通过轴对称变换,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”加以解决。
拓展应用,巩固提高
八年级某班同学做游戏,在活动区域边放了一些球,则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A处。
P
路线:小明——P——A
如果另一侧放着一些小木棍,小明先去捡球,还要跑到另一侧去取木棍,则小明又应按怎样的路线跑,去捡哪个位置的球,小木棍,才能最快跑到目的地A处。
D
E
C
路线:小明——D——E——A
如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边给马喝水,然后回到帐篷,请你帮助他确定这一天的最短路线。
如果我们把台球桌做成等边三角形的形状,那么从AC中点D处发出的球,能否依次经BC、AB两条边反射回到D处?如果你认为不能,请说明理由;如果你认为能,请作出球运动的路线。
A
B
C
D
再见
雨露学校 八年级数学备课组
观察下面的图案
(1)它们是轴对称图形吗?
(2)生活中这些图案可以代表什么含义?与同伴进行交流.
找出它们的对称轴.
什么是轴对称图形?什么叫两个图形成轴对称?
1、如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
2、对于两个图形,如果沿一条直线对折后,它们能完全重合,那么 这两个图形成轴对称,这条直线就是对称轴.
轴对称主要有哪些性质?
1、关于某条直线对称的两个图形是全等形;
2、如果两个图形关于某直线对称,那么对应点所连的线段被对称轴垂直平分;
3、成轴对称的两个图形的对应线段相等,对应角相等.
如图给出了一个图案的一半,其中的虚线是这个图案的对称轴.
(1)猜一猜:整个图案是个什么形状?
(2)如何准确地画出它的另一半?
已知对称轴 l 和一个点A如何画出点A关于 l 的对称点A’
3、点 A’ 就是点A关于 l 的对称点.
A
A’
1、过点A作对称轴 l 的垂线,垂足为B;
2、延长A B 至A’,使得BA’= A B.
B
l
1、 如何画线段AB关于直线L的
对称线段A’B’
找关键点作出其对称点!
然后连结线段.
A
B
A’
B’
B’
A’
2、如何画 ⊿ABC关于直线L的
对称⊿ A’B’C’
还是找关键点作出其对称点!
然后顺次连结线段构成三角形.
A
B
几何图形都可以看作由点组成,只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形;对于一些由直线、线段或射线组成的图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
3、如图给出了一个图案的一半,其中
的虚线 是这个图案的对称轴.
(1)整个图案是个什么形状?
(2)请准确地画出它的另一半.
仿照上面完成教科书上P41页练习1
4、请画出⊿ABC关于直线 的对称⊿ A’B’C’.
A
B
C
找关键点作出对称点!然后连结线段.
1、画出点A关于 l 的对称点A’:
( 3 )点 A’ 就是点A关于 l 的对称点.
( 1 )过点A作对称轴 l 的垂线,垂足为B;
( 2 )延长A B 至A’,使得BA’= A B.
A
A’
B
l
2、画简单平面图形的对称图形:
3、利用轴对称设计图案.
由一个平面图形得到它的轴对称的图形叫做轴对称变换。
轴对称变换
轴对称变换不会改变图形的 和
,只会改变图形 。
大小
位置
形状
下面的数据是某个时间经过轴对称变换而得来的,请问它表示的时间是多少?
利用轴对称变换以及变换后的一些特征,我们可以解决许多实际问题。
如图所示:从A地到B地有三条路可供选择,你会选择哪条路距离最短?你的理由是什么?
两点之间线段最短
如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?
P
所以泵站建在点P可使输气管线最短
如图,如果A,B在燃气管道L的同旁,泵站应修在管道的什么地方,可使所用的输气管线最短?
思考???
为什么在P点的位置修建泵站,就能使所用的管线最短呢?
总结经验:
实际上是通过轴对称变换,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”加以解决。
拓展应用,巩固提高
八年级某班同学做游戏,在活动区域边放了一些球,则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A处。
P
路线:小明——P——A
如果另一侧放着一些小木棍,小明先去捡球,还要跑到另一侧去取木棍,则小明又应按怎样的路线跑,去捡哪个位置的球,小木棍,才能最快跑到目的地A处。
D
E
C
路线:小明——D——E——A
如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边给马喝水,然后回到帐篷,请你帮助他确定这一天的最短路线。
如果我们把台球桌做成等边三角形的形状,那么从AC中点D处发出的球,能否依次经BC、AB两条边反射回到D处?如果你认为不能,请说明理由;如果你认为能,请作出球运动的路线。
A
B
C
D
再见
