北师大版九年级数学上册 第3章 概率的进一步认识 单元练习卷(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学上册 第3章 概率的进一步认识 单元练习卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 21:31:26 | ||
图片预览



文档简介
第3章 概率的进一步认识
一.选择题
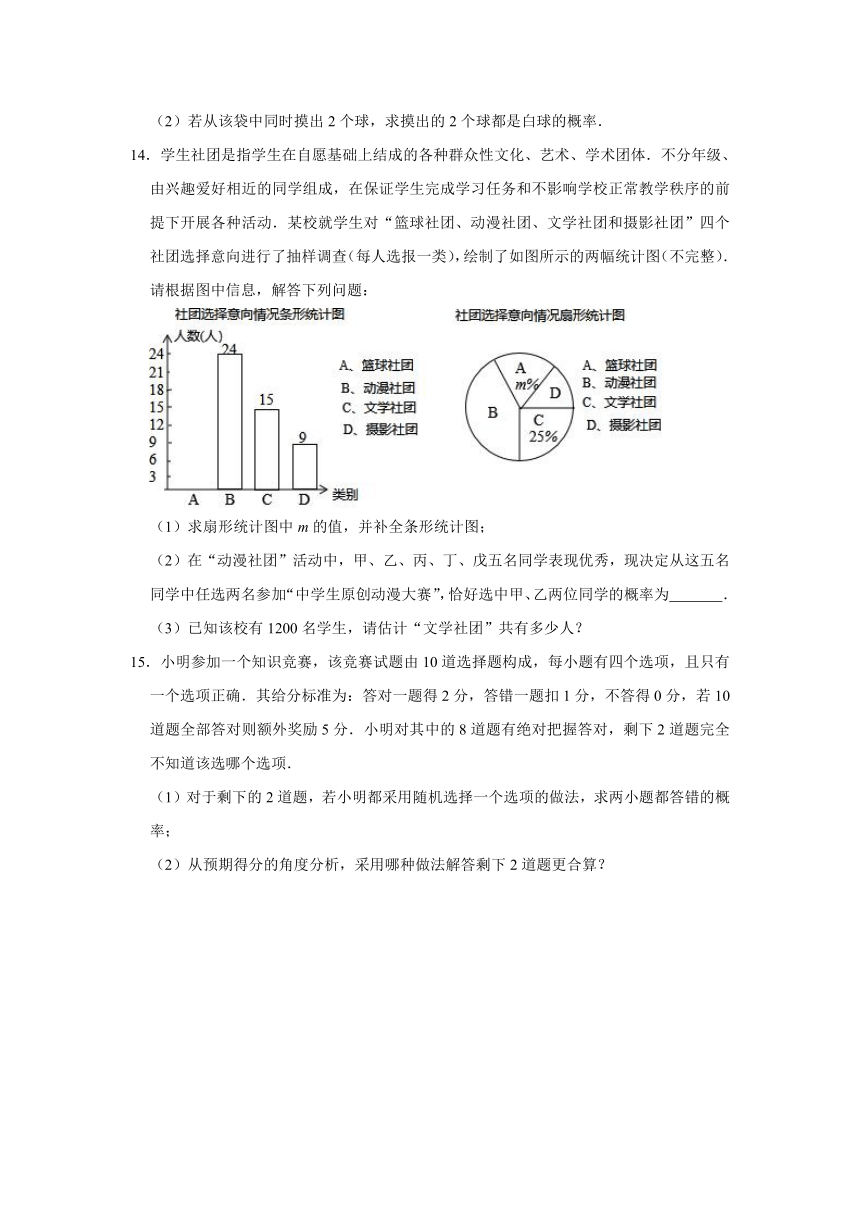
1.现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同,从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是( )
A. B. C. D.
2.不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球,两次都摸出白球的概率是( )
A. B. C. D.
3.在一个不透明的布袋中装有52个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后并放回,通过多次试验后发现,摸到黑球的频率稳定在0.2左右,则布袋中黑球的个数可能有( )
A.11 B.13 C.24 D.30
4.在一个不透明的盒子里装有200个红、黄两种颜色的小球,这些球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球,记下颜色后再放回盒子,通过大量重复试验后发现,摸到黄球的频率稳定在45%,那么估计盒子中黄球的个数为( )
A.80 B.90 C.100 D.110
5.某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82 C.0.85 D.0.84
6.某鱼塘里养了1600条鲤鱼,若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,则该鱼塘捞到鲤鱼的概率约为( )
A. B. C. D.
7.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表,若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
A.200 B.300 C.500 D.800
8.下列说法正确的是( )
A.要了解襄阳市学生在网课期间视力情况适合全面调查
B.用频率估计概率,必须建立在大量重复试验的基础上
C.打开电视机正在放广告,这是一个确定事件
D.甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明乙的跳远成绩比甲稳定
9.新冠疫情发生以来,为保证防控期间的口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,从最初转产时的陌生,到正式投产后达成日均生产100万个口罩的产能.不仅效率高,而且口罩送检合格率也不断提升,真正体现了“大国速度”.以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
抽检数量n/个 20 50 100 200 500 1000 2000 5000 10000
合格数量m/个 19 46 93 185 459 922 1840 4595 9213
口罩合格率 0.950 0.920 0.930 0.925 0.918 0.922 0.920 0.919 0.921
下面四个推断合理的是( )
A.当抽检口罩的数量是10000个时,口罩合格的数量是9213个,所以这批口罩中“口罩合格”的概率是0.921
B.由于抽检口罩的数量分别是50和2000个时,口罩合格率均是0.920,所以可以估计这批口罩中“口罩合格”的概率是0.920
C.随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩中“口罩合格”的概率是0.920
D.当抽检口罩的数量达到20000个时,“口罩合格”的概率一定是0.921
10.下列说法中,正确的是( )
A.为检测市场上正在销售的酸奶质量,应该采用全面调查的方式
B.旅客上飞机前的安检,采用抽样调查方式
C.某同学连续5次抛掷质量均匀的硬币,1次正面向上,因此正面向上的概率是20%
D.在连续6次数学测试中,两名同学的平均分相同,方差较小的同学数学成绩更稳定
11.将分别标有“武”“汉”“加”“油”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀.随机摸出一球,不放回;再随机摸出一球.两次摸出的球上的汉字能组成“加油”的概率是( )
A. B. C. D.
二.解答题
12.宿迁具有丰富的旅游资源,小明利用周日来宿迁游玩,上午从A、B、C三个景点中任意选择一个游玩,下午从D、E两个景点中任意选择一个游玩.
(1)求上午小明选中景点A的概率;
(2)用列表或画树状图的方法列出所有等可能的结果,并求小明恰好选中景点B和D的概率.
13.在一个不透明的袋子中有1个红球,2个白球和若干个黑球.小明将袋子中的球摇匀后,从中任意摸出一个球,记下颜色后放回袋中并摇匀,在多次重复以上操作后,小明统计了摸到红球的频率,并绘制了如折线统计图:
(1)袋子中一共有 个球;
(2)若从该袋中同时摸出2个球,求摸出的2个球都是白球的概率.
14.学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).
请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在“动漫社团”活动中,甲、乙、丙、丁、戊五名同学表现优秀,现决定从这五名同学中任选两名参加“中学生原创动漫大赛”,恰好选中甲、乙两位同学的概率为 .
(3)已知该校有1200名学生,请估计“文学社团”共有多少人?
15.小明参加一个知识竞赛,该竞赛试题由10道选择题构成,每小题有四个选项,且只有一个选项正确.其给分标准为:答对一题得2分,答错一题扣1分,不答得0分,若10道题全部答对则额外奖励5分.小明对其中的8道题有绝对把握答对,剩下2道题完全不知道该选哪个选项.
(1)对于剩下的2道题,若小明都采用随机选择一个选项的做法,求两小题都答错的概率;
(2)从预期得分的角度分析,采用哪种做法解答剩下2道题更合算?
参考答案
一.选择题
1. B.
2. A.
3. B.
4. B.
5. B.
6. C.
7. C.
8. B.
9. C.
10. D.
11. B.
二.解答题
12.解:(1)上午小明选中景点A的概率为;
(2)列表如下:
D E
A (A,D) (A,E)
B (B,D) (B,E)
C (C,D) (C,E)
由表可知,共有6种等可能结果,其中小明恰好选中景点B和D的只有1种结果,
∴小明恰好选中景点B和D的概率为.
13.解:(1)观察折线统计图可知:
摸到红球的频率稳定在0.2,
设袋子中有x个黑球,
所以=0.2,
解得x=2,
所以袋子中一共有5个球.
故答案为:5;
(2)解:将2个白球分别记作“白1”、“白2”,
2个黑球分别记作“黑1”、“黑2”.
从袋中同时摸出2个球,
可能出现的结果有10种,
即(红,白1),(红,白2),(红,黑1),(红,黑2),(白1,白2),(白1,黑1),(白1,黑2),(白2,黑1),(白2,黑2),(黑1,黑2),
并且它们出现的可能性相同.
其中2个球都是白球(记为事件A)的结果有1种,即(白1,白2),
所以P(A)=.
14.解:(1)本次调查的总人数为15÷25%=60(人),
∴A类别人数为:60﹣(24+15+9)=12(人),
则m%=×100%=20%,
∴m=20,
补全图形如下:
(2)列表得:
甲 乙 丙 丁 戊
甲
(甲,乙) (甲,丙) (甲,丁) (甲,戊)
乙 (乙,甲)
(乙,丙) (乙,丁) (乙,戊)
丙 (丙,甲) (丙,乙)
(丙,丁) (丙,戊)
丁 (丁,甲) (丁,乙) (丁,丙)
(丁,戊)
戊 (戊,甲) (戊,乙) (戊,丙) (戊,丁)
∵共有20种等可能的结果,恰好选中甲、乙两位同学的有2种情况,
∴恰好选中甲、乙两位同学的概率为=;
故答案为:;
(3)估计“文学社团”共有1200×25%=300(人).
15.解:(1)因为每小题有四个选项,且只有一个选项是正确的,
所以有三个选项是错误的,
不妨用“对,错,错,错”来表示.因此可列表:
由表格可知,共有16种等可能的结果,
其中两题都答错的有9种结果,
所以两小题都答错的概率为;
(2)小明有3种可能的解答方式分别为:
①两题都不答;
②一题不答,一题随机选择;
③两题都采用随机选择.
①当两题都不答时,预期得分为0+16=16分;
②当一题不答,一题随机选择时,
∵P(对)=,P(错)=,
∴预期得分为:2×﹣1×+0+16=15分;
③当两题都采用随机选择时,有两题都对,一对一错,两题都错三种可能,
所得的分数分别为9分,1分,﹣2分,
相应的概率分别为:
P(答对2题)=,
P(答对1题)=,
P(两题都答错)=,
∴预期得分为:
9×+1×﹣2×+16=15.
∵15<15<16,
∴小明采用都不答的解答方式更合算.
一.选择题
1.现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同,从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是( )
A. B. C. D.
2.不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球,两次都摸出白球的概率是( )
A. B. C. D.
3.在一个不透明的布袋中装有52个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后并放回,通过多次试验后发现,摸到黑球的频率稳定在0.2左右,则布袋中黑球的个数可能有( )
A.11 B.13 C.24 D.30
4.在一个不透明的盒子里装有200个红、黄两种颜色的小球,这些球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球,记下颜色后再放回盒子,通过大量重复试验后发现,摸到黄球的频率稳定在45%,那么估计盒子中黄球的个数为( )
A.80 B.90 C.100 D.110
5.某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中九环以上”的次数 18 68 82 168 327 823
“射中九环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90 B.0.82 C.0.85 D.0.84
6.某鱼塘里养了1600条鲤鱼,若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,则该鱼塘捞到鲤鱼的概率约为( )
A. B. C. D.
7.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表,若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
抛掷次数 100 200 300 400 500
正面朝上的频数 53 98 156 202 244
A.200 B.300 C.500 D.800
8.下列说法正确的是( )
A.要了解襄阳市学生在网课期间视力情况适合全面调查
B.用频率估计概率,必须建立在大量重复试验的基础上
C.打开电视机正在放广告,这是一个确定事件
D.甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明乙的跳远成绩比甲稳定
9.新冠疫情发生以来,为保证防控期间的口罩供应,某公司加紧转产,开设多条生产线争分夺秒赶制口罩,从最初转产时的陌生,到正式投产后达成日均生产100万个口罩的产能.不仅效率高,而且口罩送检合格率也不断提升,真正体现了“大国速度”.以下是质监局对一批口罩进行质量抽检的相关数据,统计如下:
抽检数量n/个 20 50 100 200 500 1000 2000 5000 10000
合格数量m/个 19 46 93 185 459 922 1840 4595 9213
口罩合格率 0.950 0.920 0.930 0.925 0.918 0.922 0.920 0.919 0.921
下面四个推断合理的是( )
A.当抽检口罩的数量是10000个时,口罩合格的数量是9213个,所以这批口罩中“口罩合格”的概率是0.921
B.由于抽检口罩的数量分别是50和2000个时,口罩合格率均是0.920,所以可以估计这批口罩中“口罩合格”的概率是0.920
C.随着抽检数量的增加,“口罩合格”的频率总在0.920附近摆动,显示出一定的稳定性,所以可以估计这批口罩中“口罩合格”的概率是0.920
D.当抽检口罩的数量达到20000个时,“口罩合格”的概率一定是0.921
10.下列说法中,正确的是( )
A.为检测市场上正在销售的酸奶质量,应该采用全面调查的方式
B.旅客上飞机前的安检,采用抽样调查方式
C.某同学连续5次抛掷质量均匀的硬币,1次正面向上,因此正面向上的概率是20%
D.在连续6次数学测试中,两名同学的平均分相同,方差较小的同学数学成绩更稳定
11.将分别标有“武”“汉”“加”“油”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀.随机摸出一球,不放回;再随机摸出一球.两次摸出的球上的汉字能组成“加油”的概率是( )
A. B. C. D.
二.解答题
12.宿迁具有丰富的旅游资源,小明利用周日来宿迁游玩,上午从A、B、C三个景点中任意选择一个游玩,下午从D、E两个景点中任意选择一个游玩.
(1)求上午小明选中景点A的概率;
(2)用列表或画树状图的方法列出所有等可能的结果,并求小明恰好选中景点B和D的概率.
13.在一个不透明的袋子中有1个红球,2个白球和若干个黑球.小明将袋子中的球摇匀后,从中任意摸出一个球,记下颜色后放回袋中并摇匀,在多次重复以上操作后,小明统计了摸到红球的频率,并绘制了如折线统计图:
(1)袋子中一共有 个球;
(2)若从该袋中同时摸出2个球,求摸出的2个球都是白球的概率.
14.学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).
请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在“动漫社团”活动中,甲、乙、丙、丁、戊五名同学表现优秀,现决定从这五名同学中任选两名参加“中学生原创动漫大赛”,恰好选中甲、乙两位同学的概率为 .
(3)已知该校有1200名学生,请估计“文学社团”共有多少人?
15.小明参加一个知识竞赛,该竞赛试题由10道选择题构成,每小题有四个选项,且只有一个选项正确.其给分标准为:答对一题得2分,答错一题扣1分,不答得0分,若10道题全部答对则额外奖励5分.小明对其中的8道题有绝对把握答对,剩下2道题完全不知道该选哪个选项.
(1)对于剩下的2道题,若小明都采用随机选择一个选项的做法,求两小题都答错的概率;
(2)从预期得分的角度分析,采用哪种做法解答剩下2道题更合算?
参考答案
一.选择题
1. B.
2. A.
3. B.
4. B.
5. B.
6. C.
7. C.
8. B.
9. C.
10. D.
11. B.
二.解答题
12.解:(1)上午小明选中景点A的概率为;
(2)列表如下:
D E
A (A,D) (A,E)
B (B,D) (B,E)
C (C,D) (C,E)
由表可知,共有6种等可能结果,其中小明恰好选中景点B和D的只有1种结果,
∴小明恰好选中景点B和D的概率为.
13.解:(1)观察折线统计图可知:
摸到红球的频率稳定在0.2,
设袋子中有x个黑球,
所以=0.2,
解得x=2,
所以袋子中一共有5个球.
故答案为:5;
(2)解:将2个白球分别记作“白1”、“白2”,
2个黑球分别记作“黑1”、“黑2”.
从袋中同时摸出2个球,
可能出现的结果有10种,
即(红,白1),(红,白2),(红,黑1),(红,黑2),(白1,白2),(白1,黑1),(白1,黑2),(白2,黑1),(白2,黑2),(黑1,黑2),
并且它们出现的可能性相同.
其中2个球都是白球(记为事件A)的结果有1种,即(白1,白2),
所以P(A)=.
14.解:(1)本次调查的总人数为15÷25%=60(人),
∴A类别人数为:60﹣(24+15+9)=12(人),
则m%=×100%=20%,
∴m=20,
补全图形如下:
(2)列表得:
甲 乙 丙 丁 戊
甲
(甲,乙) (甲,丙) (甲,丁) (甲,戊)
乙 (乙,甲)
(乙,丙) (乙,丁) (乙,戊)
丙 (丙,甲) (丙,乙)
(丙,丁) (丙,戊)
丁 (丁,甲) (丁,乙) (丁,丙)
(丁,戊)
戊 (戊,甲) (戊,乙) (戊,丙) (戊,丁)
∵共有20种等可能的结果,恰好选中甲、乙两位同学的有2种情况,
∴恰好选中甲、乙两位同学的概率为=;
故答案为:;
(3)估计“文学社团”共有1200×25%=300(人).
15.解:(1)因为每小题有四个选项,且只有一个选项是正确的,
所以有三个选项是错误的,
不妨用“对,错,错,错”来表示.因此可列表:
由表格可知,共有16种等可能的结果,
其中两题都答错的有9种结果,
所以两小题都答错的概率为;
(2)小明有3种可能的解答方式分别为:
①两题都不答;
②一题不答,一题随机选择;
③两题都采用随机选择.
①当两题都不答时,预期得分为0+16=16分;
②当一题不答,一题随机选择时,
∵P(对)=,P(错)=,
∴预期得分为:2×﹣1×+0+16=15分;
③当两题都采用随机选择时,有两题都对,一对一错,两题都错三种可能,
所得的分数分别为9分,1分,﹣2分,
相应的概率分别为:
P(答对2题)=,
P(答对1题)=,
P(两题都答错)=,
∴预期得分为:
9×+1×﹣2×+16=15.
∵15<15<16,
∴小明采用都不答的解答方式更合算.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
