湘 教版八年级数学上册 4.3不等式的解法1课件(17张PPT)
文档属性
| 名称 | 湘 教版八年级数学上册 4.3不等式的解法1课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 190.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 00:00:00 | ||
图片预览






文档简介
一元一次不等式的解法(1)
不等式的三个基本性质:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
知识回顾
不等式的基本性质1
不等式基本性质2
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
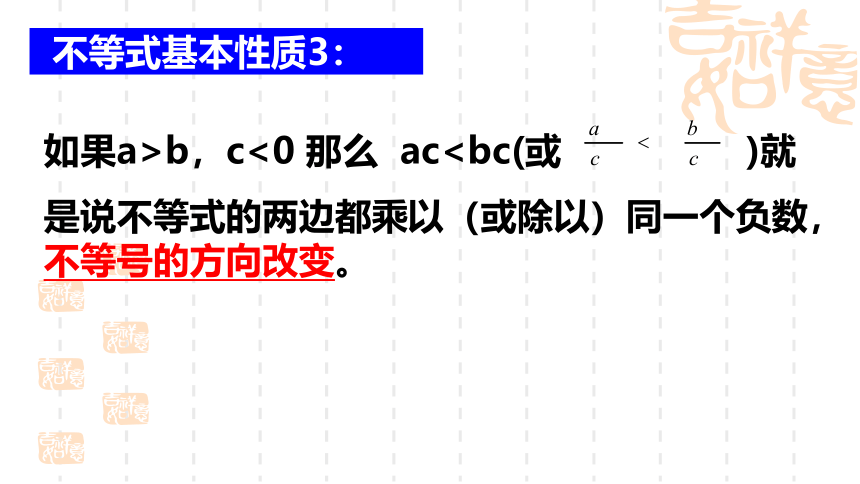
不等式基本性质3:
如果a>b,c<0 那么 ac是说不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
比一比
解:
2x=6
2x<6
x=3
x<3
解:
(1)x的2倍等于6,求x.
(2)x的2倍小于6,求x.
1.口答.
比一比
(1)x的2倍加1等于x的5倍加10 ,求x.
2、练习.
(2)x的2倍加1不小于x的5倍加10 ,求x.
解:
2x+1= 5x+10
2x-5x=+10-1
(2)
(1)
-3x=9
x=-3
2x+1≥ 5x+10
2x-5x≥+10-1
-3x≥9
x≤-3
象①2x<6, ②2x+1≥5x+10,
③3(x-2)+2<x都是一元一次不等式
由①得x<3,由②得x≤-3,由③x<2我们把得到这个结果的过程称为解不等式.
由①得1,2,2.5等都是不等式①的解,
用x<3表示2x<6的解集
一元一次不等式的概念
含有一个未知数,并且含未知数的项的次数为1的不等式,称为一元一次不等式.
不等式的解与解集
满足不等式的每一个未知数的值,称为这个不等式的解.
一个不等式的所有解的全体称为这个不等式的解集.
解不等式
求一个不等式解集的过程,称为解不等式.
解一元一次不等式与解一元一次方程的方法与步骤类似吗?
合作学习
①
⑤
④
③
②
步骤
>
6-2 (x-2) =3x
6-2x+4=3x
-2x -3x=-6-4
-5x=-10
x=2
x<2
6-2 (x-2) >3x
6-2x+4 >3x
-2x -3x >-6-4
-5x >-10
解一元一次不等式和解一元一次方程类似,有
去分母 去括号 移项 合并同类项 系数化为1
等一般步骤.
区别在哪里?
一元一次不等式的解法
在去分母和系数化为1的两步中,要特别注意不等式的两边同乘以(或除以)一个负数时,不等号的方向必须改变.
例2.解下列一元一次不等式
两边同乘以最简公分母
乘法分配律
将项从一边移到另一边
系数相加,字母指数不变
两边同时除以未知数系数
①
⑤
④
③
②
步 骤
去分母
去括号
移项
合并同类项
系数化为1
具体做法
合作学习
类比归纳解一元一次不等式的一般步骤,并指出每个步骤的具体做法.
注意:1.不要漏乘;2.符号问题;3.系数化1时不等号方向; 4.写解集时,字母写在不等号左边。
2.解下列不等式
(1)
(2) .
练习:
火眼金睛
请指出上面的解题过程中,有什么地方产生了错误。
答:在第①步中_ ________________________,在第②步中______________ __,在第③步中 ___ _________,在第④步中_______。
两边同乘-6,不等号没有变号
去分母时,应加括号
移项没有变号
正确
1.解不等式
解:
③
①
②
④
课堂检测
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得,
去括号得,
移项得,
合并同类项得,
化系数为1得,
解:
同乘最简公分母12,方向不变
同除以-7,不等号方向改变
课堂检测
3.当x取何值时,代数式 与 的值的差大于1?
解:根据题意,得
2(x+4)-3(3x-1)>6,
2x+8-9x+3>6,
2x-9x>6-8-3,
-7x>-5,
∴
∴当 的任何数时,代数式 与 的差大于1。
例3.已知: 3(5x+2)+5<4x-6(x+1),
化简:|x+1|-x
例4.不等式 的解集是x>2,
求a的值.(小组讨论)
不等式的三个基本性质:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
知识回顾
不等式的基本性质1
不等式基本性质2
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0 那么 ac
比一比
解:
2x=6
2x<6
x=3
x<3
解:
(1)x的2倍等于6,求x.
(2)x的2倍小于6,求x.
1.口答.
比一比
(1)x的2倍加1等于x的5倍加10 ,求x.
2、练习.
(2)x的2倍加1不小于x的5倍加10 ,求x.
解:
2x+1= 5x+10
2x-5x=+10-1
(2)
(1)
-3x=9
x=-3
2x+1≥ 5x+10
2x-5x≥+10-1
-3x≥9
x≤-3
象①2x<6, ②2x+1≥5x+10,
③3(x-2)+2<x都是一元一次不等式
由①得x<3,由②得x≤-3,由③x<2我们把得到这个结果的过程称为解不等式.
由①得1,2,2.5等都是不等式①的解,
用x<3表示2x<6的解集
一元一次不等式的概念
含有一个未知数,并且含未知数的项的次数为1的不等式,称为一元一次不等式.
不等式的解与解集
满足不等式的每一个未知数的值,称为这个不等式的解.
一个不等式的所有解的全体称为这个不等式的解集.
解不等式
求一个不等式解集的过程,称为解不等式.
解一元一次不等式与解一元一次方程的方法与步骤类似吗?
合作学习
①
⑤
④
③
②
步骤
>
6-2 (x-2) =3x
6-2x+4=3x
-2x -3x=-6-4
-5x=-10
x=2
x<2
6-2 (x-2) >3x
6-2x+4 >3x
-2x -3x >-6-4
-5x >-10
解一元一次不等式和解一元一次方程类似,有
去分母 去括号 移项 合并同类项 系数化为1
等一般步骤.
区别在哪里?
一元一次不等式的解法
在去分母和系数化为1的两步中,要特别注意不等式的两边同乘以(或除以)一个负数时,不等号的方向必须改变.
例2.解下列一元一次不等式
两边同乘以最简公分母
乘法分配律
将项从一边移到另一边
系数相加,字母指数不变
两边同时除以未知数系数
①
⑤
④
③
②
步 骤
去分母
去括号
移项
合并同类项
系数化为1
具体做法
合作学习
类比归纳解一元一次不等式的一般步骤,并指出每个步骤的具体做法.
注意:1.不要漏乘;2.符号问题;3.系数化1时不等号方向; 4.写解集时,字母写在不等号左边。
2.解下列不等式
(1)
(2) .
练习:
火眼金睛
请指出上面的解题过程中,有什么地方产生了错误。
答:在第①步中_ ________________________,在第②步中______________ __,在第③步中 ___ _________,在第④步中_______。
两边同乘-6,不等号没有变号
去分母时,应加括号
移项没有变号
正确
1.解不等式
解:
③
①
②
④
课堂检测
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得,
去括号得,
移项得,
合并同类项得,
化系数为1得,
解:
同乘最简公分母12,方向不变
同除以-7,不等号方向改变
课堂检测
3.当x取何值时,代数式 与 的值的差大于1?
解:根据题意,得
2(x+4)-3(3x-1)>6,
2x+8-9x+3>6,
2x-9x>6-8-3,
-7x>-5,
∴
∴当 的任何数时,代数式 与 的差大于1。
例3.已知: 3(5x+2)+5<4x-6(x+1),
化简:|x+1|-x
例4.不等式 的解集是x>2,
求a的值.(小组讨论)
同课章节目录
