苏科版九年级上册数学课件:2.4圆周角(23张)
文档属性
| 名称 | 苏科版九年级上册数学课件:2.4圆周角(23张) |  | |
| 格式 | pptx | ||
| 文件大小 | 390.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 10:20:03 | ||
图片预览




文档简介
让我们一起,
继续探究,
圆的奥秘 ……
Q
P
O
B
A
C
顶点在圆心的角叫做圆心角.
回顾
圆周角
苏科版 数学
九年级(上册)
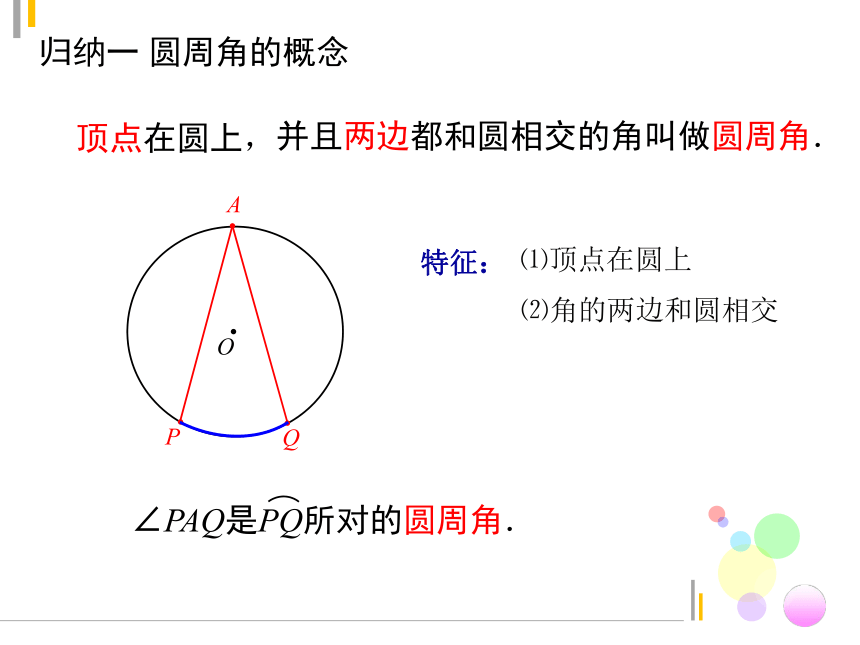
归纳一 圆周角的概念
Q
P
O
A
顶点在圆上,
并且两边都和圆相交的角叫做圆周角.
∠PAQ是PQ所对的圆周角.
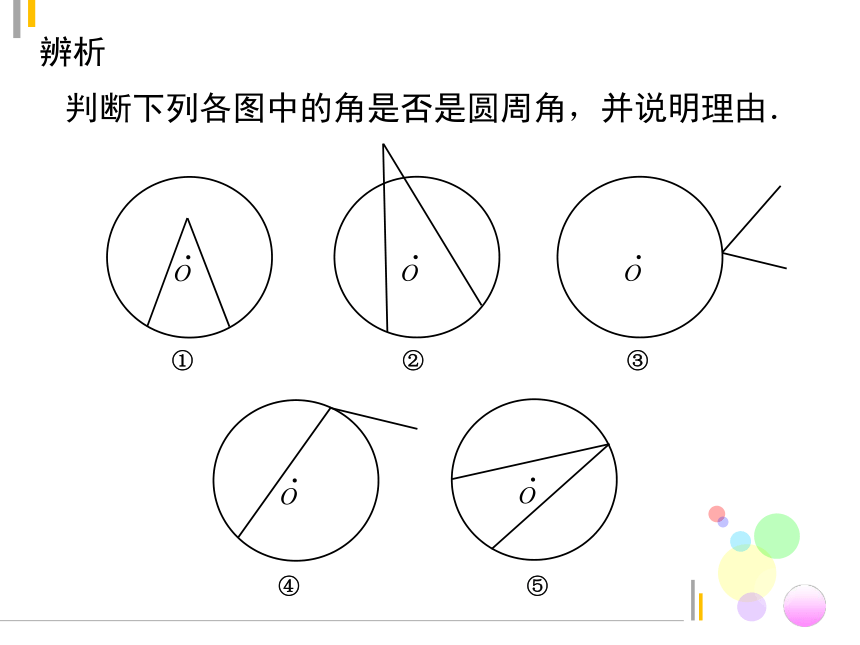
辨析
判断下列各图中的角是否是圆周角,并说明理由.
O
O
O
O
O
① ② ③
④ ⑤
归纳一 圆周角的概念
Q
P
O
A
顶点在圆上,
并且两边都和圆相交的角叫做圆周角.
∠PAQ是PQ所对的圆周角.
⑴顶点在圆上
⑵角的两边和圆相交
特征:
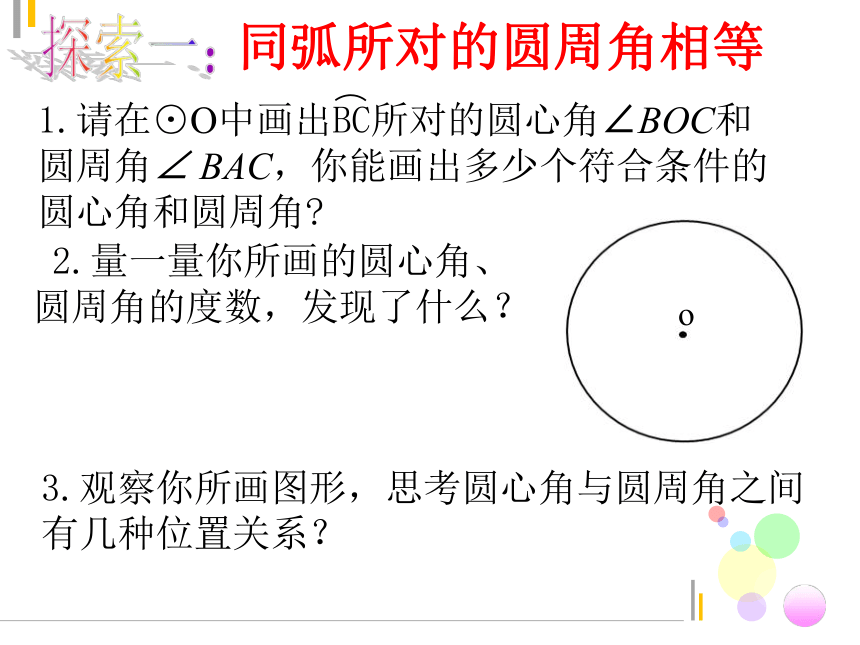
2.量一量你所画的圆心角、
圆周角的度数,发现了什么?
1.请在⊙O中画出BC所对的圆心角∠BOC和圆周角∠ BAC,你能画出多少个符合条件的圆心角和圆周角?
3.观察你所画图形,思考圆心角与圆周角之间有几种位置关系?
探索一:
同弧所对的圆周角相等
o
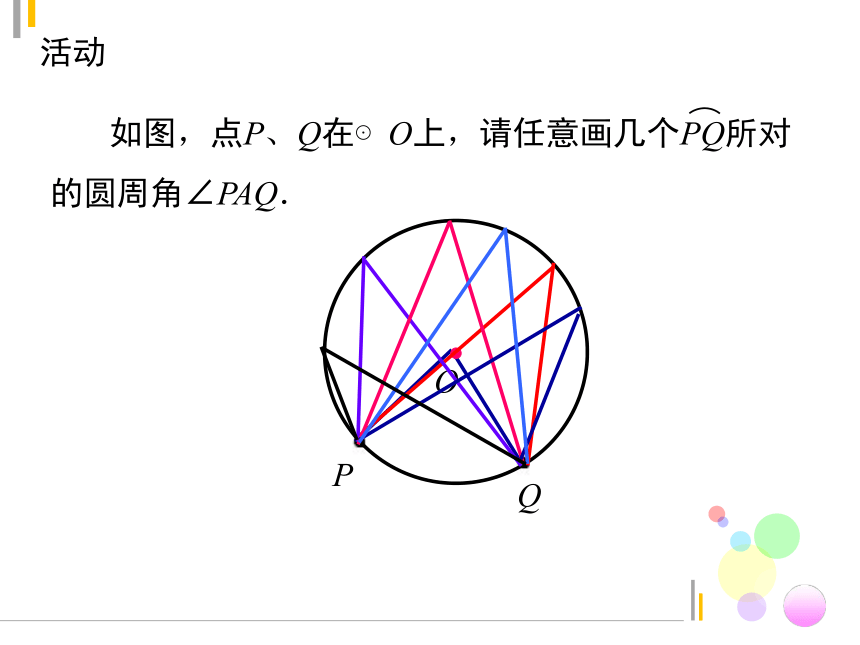
活动
如图,点P、Q在⊙O上,请任意画几个PQ所对的圆周角∠PAQ.
Q
P
O
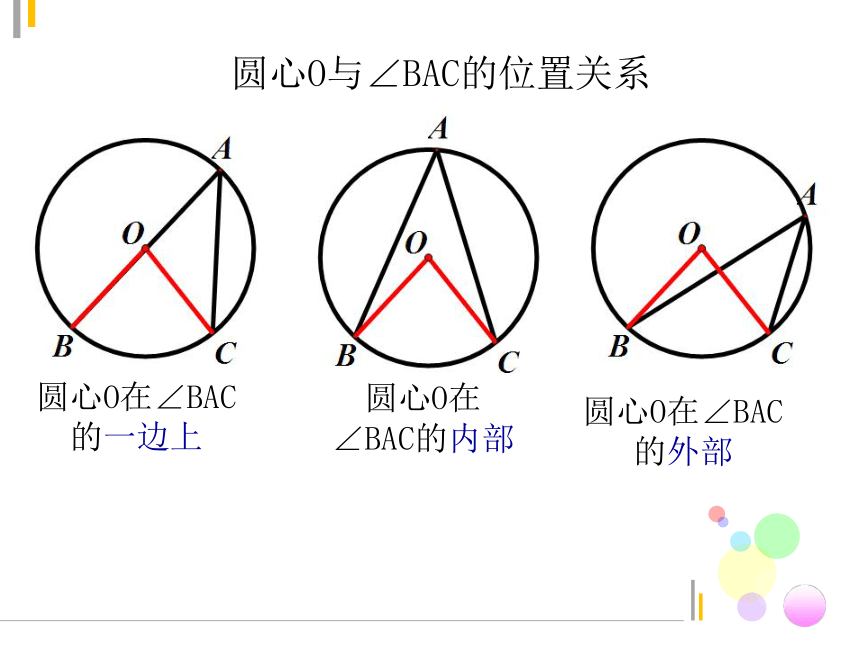
圆心O与∠BAC的位置关系
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
探索二:
∟
O
90°
B
A
C
A
⌒
120°
B
C
O
⌒
A
B
C
n°
O
你发现了什么?
45°
60°
如图,AB为⊙O的直径,∠BOC、∠BAC分别是BC 所对的圆心角、圆周角,求出图中∠BAC的度数.
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
O
A
B
D
O
A
C
D
O
A
B
C
D
O
A
C
D
O
A
B
D
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
归纳二
O
Q
P
A
A
A
圆周角定理:
同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角度数的一半。
试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
例题
例题
2. 如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,AC、BD交于点G.请比较∠BAC与∠BDC的大小.
C
A
O
F
B
D
E
G
新知应用
1、如图,点A、B、C、D在⊙O上,点A与点D在点B、 C所在直线的同侧,∠BAC=35°
(1)∠BDC=______ °,理由是________
(2)∠BOC=______ °,理由是________
2、如图,AB、AC是⊙O的弦,延长CA到点D,使AD=AB,若∠D=20°,则∠BOC=_______。
归纳小结
1.圆周角定义:
顶点在圆上,
并且两边都和圆相交的角叫做圆周角.
同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半.
2.圆周角定理:
作业:课后布置
谢谢!
继续探究,
圆的奥秘 ……
Q
P
O
B
A
C
顶点在圆心的角叫做圆心角.
回顾
圆周角
苏科版 数学
九年级(上册)
归纳一 圆周角的概念
Q
P
O
A
顶点在圆上,
并且两边都和圆相交的角叫做圆周角.
∠PAQ是PQ所对的圆周角.
辨析
判断下列各图中的角是否是圆周角,并说明理由.
O
O
O
O
O
① ② ③
④ ⑤
归纳一 圆周角的概念
Q
P
O
A
顶点在圆上,
并且两边都和圆相交的角叫做圆周角.
∠PAQ是PQ所对的圆周角.
⑴顶点在圆上
⑵角的两边和圆相交
特征:
2.量一量你所画的圆心角、
圆周角的度数,发现了什么?
1.请在⊙O中画出BC所对的圆心角∠BOC和圆周角∠ BAC,你能画出多少个符合条件的圆心角和圆周角?
3.观察你所画图形,思考圆心角与圆周角之间有几种位置关系?
探索一:
同弧所对的圆周角相等
o
活动
如图,点P、Q在⊙O上,请任意画几个PQ所对的圆周角∠PAQ.
Q
P
O
圆心O与∠BAC的位置关系
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
探索二:
∟
O
90°
B
A
C
A
⌒
120°
B
C
O
⌒
A
B
C
n°
O
你发现了什么?
45°
60°
如图,AB为⊙O的直径,∠BOC、∠BAC分别是BC 所对的圆心角、圆周角,求出图中∠BAC的度数.
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
O
A
B
D
O
A
C
D
O
A
B
C
D
O
A
C
D
O
A
B
D
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
已知:⊙O中,BC所对的圆周角是∠BAC,圆心角是∠BOC。
求证:∠BAC= ∠BOC
归纳二
O
Q
P
A
A
A
圆周角定理:
同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角度数的一半。
试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
例题
例题
2. 如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,AC、BD交于点G.请比较∠BAC与∠BDC的大小.
C
A
O
F
B
D
E
G
新知应用
1、如图,点A、B、C、D在⊙O上,点A与点D在点B、 C所在直线的同侧,∠BAC=35°
(1)∠BDC=______ °,理由是________
(2)∠BOC=______ °,理由是________
2、如图,AB、AC是⊙O的弦,延长CA到点D,使AD=AB,若∠D=20°,则∠BOC=_______。
归纳小结
1.圆周角定义:
顶点在圆上,
并且两边都和圆相交的角叫做圆周角.
同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半.
2.圆周角定理:
作业:课后布置
谢谢!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
