人教版八年级上册14.3.2运用完全平方公式分解因式课件(17张PPT)
文档属性
| 名称 | 人教版八年级上册14.3.2运用完全平方公式分解因式课件(17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 563.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 16:23:08 | ||
图片预览




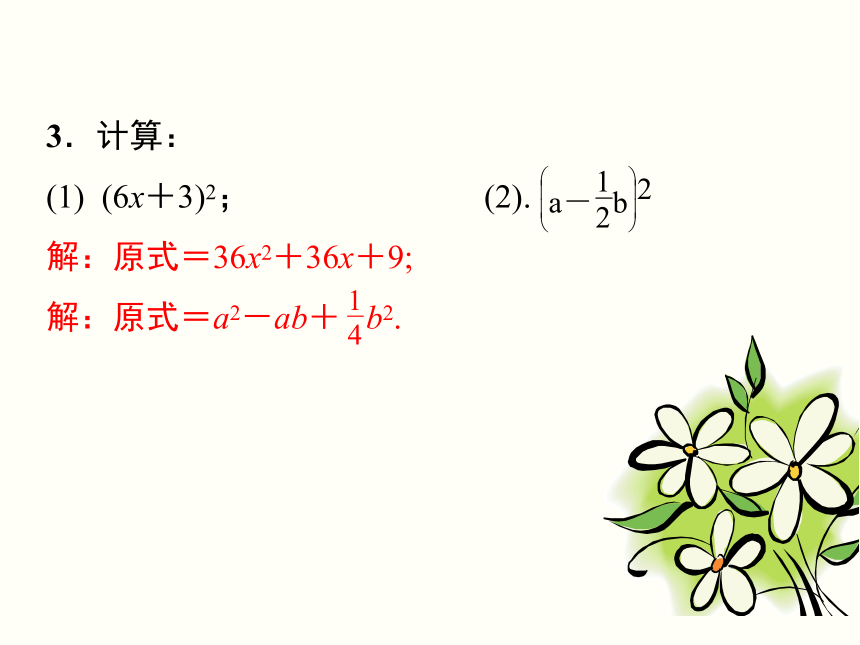


文档简介
第2课时 运用完全平方公式分解因式
一、教学目标
1.掌握完全平方公式的特点.
2.运用完全平方公式进行因式分解.
重点
难点
二、教学重难点
掌握完全平方公式的特点,并会用完全平方公式进行因式分解.
灵活运用完全平方公式进行因式分解.
活动1 新课导入
三、教学设计
1.乘法的完全平方公式:
(a+b)2=a2+____+b2;
(a-b)2=a2-____+b2.
2.填空:
(1) (5x-____)2=____-10xy+y2;
(2) (____+____)2=4a2+12ab+9b2.
3b
2ab
2ab
y
25x2
2a
3.计算:
(1) (6x+3)2; (2).
解:原式=36x2+36x+9;
解:原式=a2-ab+ b2.
活动2 探究新知
1、思考
提出问题:
(1) 整式乘法的完全平方公式有多少个?它们分别是什么?
(2) 多项式a2+2ab+b2与a2-2ab+b2有什么特点?它们是完全平方式吗?它们与整式的完全平方公式有什么关系?
(3) 你能将a2+2ab+b2和a2-2ab+b2分解因式吗?
解: (1) 3ax2+6axy+3ay2
= 3a(x2+2xy+y2)
= 3a(x+y)2;
2、例6 分解因式:
3ax2+6axy+3ay2; (2) (a+b)2 - 12(a+b)+36.
分析:(1)中有公因式3a,应先提出公因式,再进一步
分解;(2)中,将a+b看作一个整体,设a+b=m,则原
式化为完全平方式m2-12m+36.
(2) (a+b)2 - 12(a+b)+36
= (a+b)2 -2·(a+b)·6+62
= (a+b-6)2
提出问题:
(1)例6第(1)小题的因式分解过程给我们什么启示?
(2)例6第(2)小题的因式分解过程给我们什么启示?
活动3 知识归纳
1.两个数的平方和加上这两个数的________,等于这两个数的__的平方.用字母表示为a2+2ab+b2=______ .
2.两个数的平方和减去这两个数的________,等于这两个数的__的平方.用字母表示为a2-2ab+b2=______.
3.像a2+2ab+b2,a2-2ab+b2这样的式子叫做__________.
完全平方式
积的2倍
和
(a+b)2
积的2倍
差
(a-b)2
4.把乘法公式的等号两边________,就可以得到用于分解因式的公式,用来把某些具有特殊形式的多项式分解因式,这种分解因式的方法叫做_______.
互换位置
公式法
活动4 例题与练习
例1 分解因式:
(1) 16x?+24x+9; (2) -x?+4xy - 4y? .
分析:在(1)中,16x?= (4x)?,9=3?,24x=2·4x·3,所以16x?+24x+9是一个完全平方公式,即
16x?+24x+9= (4x)? + 2 · 4x · 3 + 3?.
a? + 2 · a · b + b?
解:(1) 16x?+24x+9
= (4x)? + 2·4x·3 + 3?
= (4x+3)? ;
(2) -x?+4xy - 4y?
= -(x?-4xy+4y?)
= -[x?-2·x·2y+(2y)?]
= -(x-2y)?.
例2 分解因式:
(1) a2+ab+ b2;
解:原式= ;
(2) -2x3y+4x2y-2xy;
解:原式 =-2xy(x2-2x+1)
=-2xy(x-1)2;
(3) (a-b)2-6(b-a)+9;
解:原式 = (a-b)2+6(a-b)+9
= (a-b+3)2;
(4) (x2-2x)2+2(x2-2x)+1.
解:原式 = (x2-2x+1)2
= [(x-1)2]2=(x-1)4.
练 习
1.教材P119 练习第1,2题.
2.分解因式:
(1) (a2-4a)2+8(a2-4a)+16;(2) 2x2-12x+18
(3) x2+xy+ y2; (4) abx2+2abxy+aby2.
解:原式=(a-2)4;
解:原式=2(x-3) 2.
解:原式= (x+y)2;
解:原式=ab(x+y)2.
一、教学目标
1.掌握完全平方公式的特点.
2.运用完全平方公式进行因式分解.
重点
难点
二、教学重难点
掌握完全平方公式的特点,并会用完全平方公式进行因式分解.
灵活运用完全平方公式进行因式分解.
活动1 新课导入
三、教学设计
1.乘法的完全平方公式:
(a+b)2=a2+____+b2;
(a-b)2=a2-____+b2.
2.填空:
(1) (5x-____)2=____-10xy+y2;
(2) (____+____)2=4a2+12ab+9b2.
3b
2ab
2ab
y
25x2
2a
3.计算:
(1) (6x+3)2; (2).
解:原式=36x2+36x+9;
解:原式=a2-ab+ b2.
活动2 探究新知
1、思考
提出问题:
(1) 整式乘法的完全平方公式有多少个?它们分别是什么?
(2) 多项式a2+2ab+b2与a2-2ab+b2有什么特点?它们是完全平方式吗?它们与整式的完全平方公式有什么关系?
(3) 你能将a2+2ab+b2和a2-2ab+b2分解因式吗?
解: (1) 3ax2+6axy+3ay2
= 3a(x2+2xy+y2)
= 3a(x+y)2;
2、例6 分解因式:
3ax2+6axy+3ay2; (2) (a+b)2 - 12(a+b)+36.
分析:(1)中有公因式3a,应先提出公因式,再进一步
分解;(2)中,将a+b看作一个整体,设a+b=m,则原
式化为完全平方式m2-12m+36.
(2) (a+b)2 - 12(a+b)+36
= (a+b)2 -2·(a+b)·6+62
= (a+b-6)2
提出问题:
(1)例6第(1)小题的因式分解过程给我们什么启示?
(2)例6第(2)小题的因式分解过程给我们什么启示?
活动3 知识归纳
1.两个数的平方和加上这两个数的________,等于这两个数的__的平方.用字母表示为a2+2ab+b2=______ .
2.两个数的平方和减去这两个数的________,等于这两个数的__的平方.用字母表示为a2-2ab+b2=______.
3.像a2+2ab+b2,a2-2ab+b2这样的式子叫做__________.
完全平方式
积的2倍
和
(a+b)2
积的2倍
差
(a-b)2
4.把乘法公式的等号两边________,就可以得到用于分解因式的公式,用来把某些具有特殊形式的多项式分解因式,这种分解因式的方法叫做_______.
互换位置
公式法
活动4 例题与练习
例1 分解因式:
(1) 16x?+24x+9; (2) -x?+4xy - 4y? .
分析:在(1)中,16x?= (4x)?,9=3?,24x=2·4x·3,所以16x?+24x+9是一个完全平方公式,即
16x?+24x+9= (4x)? + 2 · 4x · 3 + 3?.
a? + 2 · a · b + b?
解:(1) 16x?+24x+9
= (4x)? + 2·4x·3 + 3?
= (4x+3)? ;
(2) -x?+4xy - 4y?
= -(x?-4xy+4y?)
= -[x?-2·x·2y+(2y)?]
= -(x-2y)?.
例2 分解因式:
(1) a2+ab+ b2;
解:原式= ;
(2) -2x3y+4x2y-2xy;
解:原式 =-2xy(x2-2x+1)
=-2xy(x-1)2;
(3) (a-b)2-6(b-a)+9;
解:原式 = (a-b)2+6(a-b)+9
= (a-b+3)2;
(4) (x2-2x)2+2(x2-2x)+1.
解:原式 = (x2-2x+1)2
= [(x-1)2]2=(x-1)4.
练 习
1.教材P119 练习第1,2题.
2.分解因式:
(1) (a2-4a)2+8(a2-4a)+16;(2) 2x2-12x+18
(3) x2+xy+ y2; (4) abx2+2abxy+aby2.
解:原式=(a-2)4;
解:原式=2(x-3) 2.
解:原式= (x+y)2;
解:原式=ab(x+y)2.
