北师大版八年级数学上册4.1 函数课件(共34张PPT)
文档属性
| 名称 | 北师大版八年级数学上册4.1 函数课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 15:28:57 | ||
图片预览







文档简介
(共34张PPT)
4.1
函数
第四章
一次函数
北师大版八年级数学上册
学习目标
1.掌握函数的概念以及表示方法.(重点)
2.会求函数的值,并确定自变量的取值范围.(难点)
人间四月芳菲尽,
山寺桃花始盛开。
白居易
高处不胜寒
苏轼
情境引入
导入新课
早穿皮袄午穿纱,围着火炉吃西瓜,
说明__________随______的变化而变化.
高处不胜寒,说明
____________随____________的变化而变化.
天气温度
时间
高山气温
海拔高度
万物皆变,大到天体、小到分子都处在不停的运动变化之中,如何从数学的角度来刻画这些运动变化并寻找规律呢?
讲授新课
函数的概念及表示方法
一
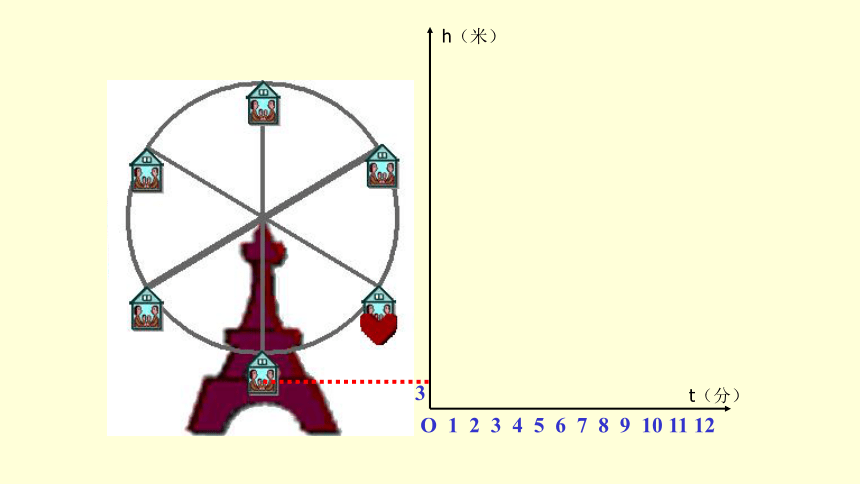
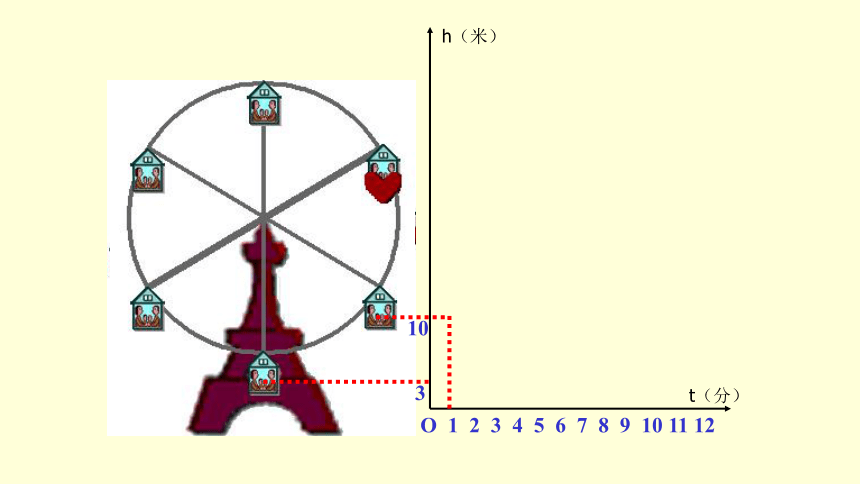
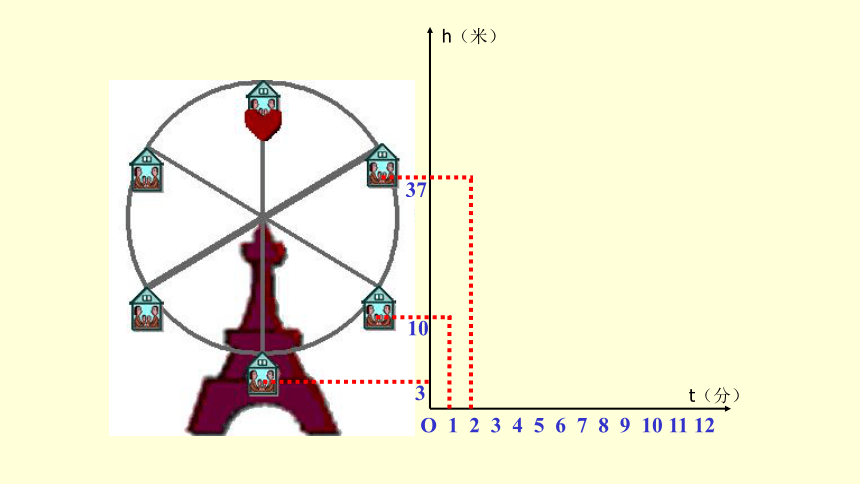
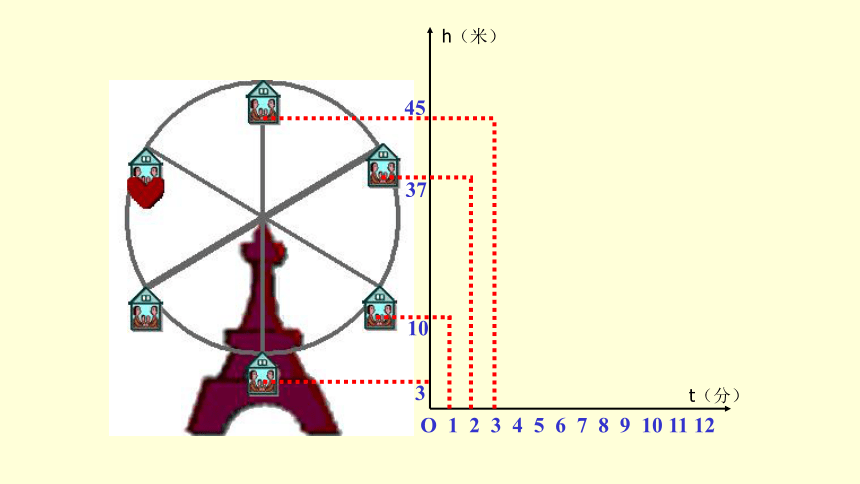
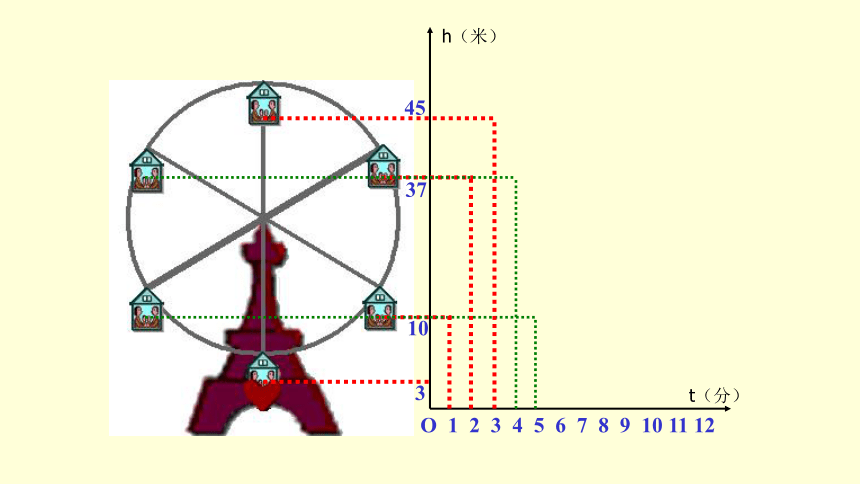
想一想,如果你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
情景一
O
1
2
3
4
5
6
7
8
9
10
11
12
3
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
45
h(米)
t(分)
下图反映了摩天轮上的一点的高度h
(m)与旋转时间t(min)
之间的关系.
T/分
0
1
2
3
4
5
…
h/米
…
(1)根据左图填表:
(2)对于给定的时间t
,相应的高度h确定吗?
11
37
45
37
3
10
瓶子或罐头盒等圆柱形的物体,常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
填写下表:
1
2
3
4
5
…
…
1
3
6
10
15
对于给定任一层数n,相应的物体总数y确定吗?有几个y值和它对应?
层数
n
物体总数y
唯一一个y值
情景二
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少?
(2)给定任一个大于-273
℃的摄氏温度t值,相应的热力学温度T确定吗?有几个T值和它对应?
230K、246K
、273K、291K
唯一一个T值
解:当t=-43时,
T=-43+273=230(K)
情景三
上面的三个问题中,有什么共同特点?
①时间
t
、相应的高度
h
;
②层数n、物体总数y;
③摄氏温度t
、热力学温度T.
共同特点:都有两个变量,给定其中某一个变量的值,相应地就确定了另一个变量的值.
归纳总结
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量.
函数
注意:
函数不是数,它是指某一变化过程中两个变量之间的关系.
表示函数
的一般方法
列表法
图象法
关系式法(解析式法、表达式法)
情景一
情景二
情景三
归纳总结
讨论:
1.y与x
的图象如图所示,问y是x的函数吗?
x
y
o
1
2
-2
y不是x的函数
2.下列各图中,x是自变量,则y是x的函数吗?为什么?
y是x的函数
y不是x的函数
3、
下列关于变量x
,y
的关系式:?y
=2x+3;?y
=x2+3;?y
=2|x|;④
y2-3x=10,其中表示y
是x
的函数关系的是
.
???
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量有唯一确定的值与它对应.
方法
自变量的取值范围
二
问题:上述的三个问题中,要使函数有意义,自变量能取哪些值?
自变量t的取值范围:__________
t≥0
情景一
1
2
3
4
5
…
…
1
3
6
10
15
层数
n
物体总数y
情景二
罐头盒等圆柱形的物体常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
自变量n的取值范围:_________.
n取正整数
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
情景三
自变量t的取值范围:___________.
t≥-273
函数值
三
T(K)与
t(℃)的函数关系:
T=
t+273
(T≥
0),
当t=1时,
T=1+273
=274(K).
那么,274就是当t=1时的函数值.
情景三
函数值
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值.
即:如果y是x的函数,当x=a时,y=b,那么b叫做当x=a时的函数值.
注意:函数不是数,它是指某一变化过程中两个变量之间的关系.而函数值是一个数,它是自变量确定时对应的因变量的值.
归纳总结
例:
已知函数
求当x=2,3,-3时,函数的值;
解:当x=2时,y=
;
当x=3时,y=
;
当x=-3时,y=7;
把自变量x的值带入关系式中,即可求出函数的值.
课堂检测(共50分,用时7分钟)
1.设路程为s,时间为t,速度为v,当v=60时,路程和时间的关系式为
,这个关系式中,
是常量,
是变量,
是
的函数.(每空3分)
60
s=60t
t和s
s
t
2.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是
。(5分)
3.(5分)下列各表达式不是表示y是x的函数的是(
)
A.
B.
C.
D.
C
4.(5分)小明的爸爸早晨出去散步,从家走了20
min到达距离家800
m的公园,他在公园休息了10
min,然后用30
min原路返回家中,那么小明的爸爸离家的距离s(单位:m)与离家的时间t(单位:
min)之间的函数关系图象大致是(
)
D
5.我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值(15分)
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数吗?
为什么?(5分)
当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
函数
定义:自变量、因变量、常量
课堂小结
表示函数的方法:三种表示方法
函数值
自变量的取值范围
课下作业
1、必做:课本习题4.1第1、2题;
2、选做:课本习题4.1第3、4题;
3、预习课本4.2一次函数与正比例函数。
4.1
函数
第四章
一次函数
北师大版八年级数学上册
学习目标
1.掌握函数的概念以及表示方法.(重点)
2.会求函数的值,并确定自变量的取值范围.(难点)
人间四月芳菲尽,
山寺桃花始盛开。
白居易
高处不胜寒
苏轼
情境引入
导入新课
早穿皮袄午穿纱,围着火炉吃西瓜,
说明__________随______的变化而变化.
高处不胜寒,说明
____________随____________的变化而变化.
天气温度
时间
高山气温
海拔高度
万物皆变,大到天体、小到分子都处在不停的运动变化之中,如何从数学的角度来刻画这些运动变化并寻找规律呢?
讲授新课
函数的概念及表示方法
一
想一想,如果你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
情景一
O
1
2
3
4
5
6
7
8
9
10
11
12
3
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
10
37
45
h(米)
t(分)
下图反映了摩天轮上的一点的高度h
(m)与旋转时间t(min)
之间的关系.
T/分
0
1
2
3
4
5
…
h/米
…
(1)根据左图填表:
(2)对于给定的时间t
,相应的高度h确定吗?
11
37
45
37
3
10
瓶子或罐头盒等圆柱形的物体,常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
填写下表:
1
2
3
4
5
…
…
1
3
6
10
15
对于给定任一层数n,相应的物体总数y确定吗?有几个y值和它对应?
层数
n
物体总数y
唯一一个y值
情景二
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少?
(2)给定任一个大于-273
℃的摄氏温度t值,相应的热力学温度T确定吗?有几个T值和它对应?
230K、246K
、273K、291K
唯一一个T值
解:当t=-43时,
T=-43+273=230(K)
情景三
上面的三个问题中,有什么共同特点?
①时间
t
、相应的高度
h
;
②层数n、物体总数y;
③摄氏温度t
、热力学温度T.
共同特点:都有两个变量,给定其中某一个变量的值,相应地就确定了另一个变量的值.
归纳总结
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量.
函数
注意:
函数不是数,它是指某一变化过程中两个变量之间的关系.
表示函数
的一般方法
列表法
图象法
关系式法(解析式法、表达式法)
情景一
情景二
情景三
归纳总结
讨论:
1.y与x
的图象如图所示,问y是x的函数吗?
x
y
o
1
2
-2
y不是x的函数
2.下列各图中,x是自变量,则y是x的函数吗?为什么?
y是x的函数
y不是x的函数
3、
下列关于变量x
,y
的关系式:?y
=2x+3;?y
=x2+3;?y
=2|x|;④
y2-3x=10,其中表示y
是x
的函数关系的是
.
???
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量有唯一确定的值与它对应.
方法
自变量的取值范围
二
问题:上述的三个问题中,要使函数有意义,自变量能取哪些值?
自变量t的取值范围:__________
t≥0
情景一
1
2
3
4
5
…
…
1
3
6
10
15
层数
n
物体总数y
情景二
罐头盒等圆柱形的物体常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
自变量n的取值范围:_________.
n取正整数
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
情景三
自变量t的取值范围:___________.
t≥-273
函数值
三
T(K)与
t(℃)的函数关系:
T=
t+273
(T≥
0),
当t=1时,
T=1+273
=274(K).
那么,274就是当t=1时的函数值.
情景三
函数值
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值.
即:如果y是x的函数,当x=a时,y=b,那么b叫做当x=a时的函数值.
注意:函数不是数,它是指某一变化过程中两个变量之间的关系.而函数值是一个数,它是自变量确定时对应的因变量的值.
归纳总结
例:
已知函数
求当x=2,3,-3时,函数的值;
解:当x=2时,y=
;
当x=3时,y=
;
当x=-3时,y=7;
把自变量x的值带入关系式中,即可求出函数的值.
课堂检测(共50分,用时7分钟)
1.设路程为s,时间为t,速度为v,当v=60时,路程和时间的关系式为
,这个关系式中,
是常量,
是变量,
是
的函数.(每空3分)
60
s=60t
t和s
s
t
2.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是
。(5分)
3.(5分)下列各表达式不是表示y是x的函数的是(
)
A.
B.
C.
D.
C
4.(5分)小明的爸爸早晨出去散步,从家走了20
min到达距离家800
m的公园,他在公园休息了10
min,然后用30
min原路返回家中,那么小明的爸爸离家的距离s(单位:m)与离家的时间t(单位:
min)之间的函数关系图象大致是(
)
D
5.我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值(15分)
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数吗?
为什么?(5分)
当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
函数
定义:自变量、因变量、常量
课堂小结
表示函数的方法:三种表示方法
函数值
自变量的取值范围
课下作业
1、必做:课本习题4.1第1、2题;
2、选做:课本习题4.1第3、4题;
3、预习课本4.2一次函数与正比例函数。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
