2020年秋北师大版数学九年级上册第六章《6.1 反比例函数》课件(20张PPT)
文档属性
| 名称 | 2020年秋北师大版数学九年级上册第六章《6.1 反比例函数》课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 931.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
北师大版数学九年级上册
第六章
反比例函数
6.1
反比例函数
1.领会反比例函数的意义,理解反比例函数的概念,了解反比例函数三种表达式.
2.能根据现实情境确定反比例函数的解析式.
学习目标
我们在前面学过一次函数和正比例函数,知道一次函数的表达式为y=kx+b(其中k,b为常数且k≠0),正比例函数的表达式为y=kx(k为常数且k≠0),在现实生活中,并不是只有这两种类型的表达式,如从A到B地的路程为1200km,某人开车从A地到B地,汽车的速度v(km/h)和时间t(h)之间的关系式为vt=1200,则
中,t和v之间肯定不是正比例函数和一次函数关系,那么它们之间究竟是什么关系呢?这就是本节课我们要揭开的奥秘.
回顾旧知
知识模块 反比例函数的概念及应用
(一)自主探究
电流I,电压U,电阻R之间满足关系式
.当U=220V时,
(1)你能用含R的代数式表示I吗?
U=IR
探究新知
当R越来越大时,
I怎样变化?
当R越来越小呢?
(3)变量I是R的函数吗?为什么?
当R越来越大时,I越来越小;反之I越来越大.
由关系式可知二者是反比例函数关系.
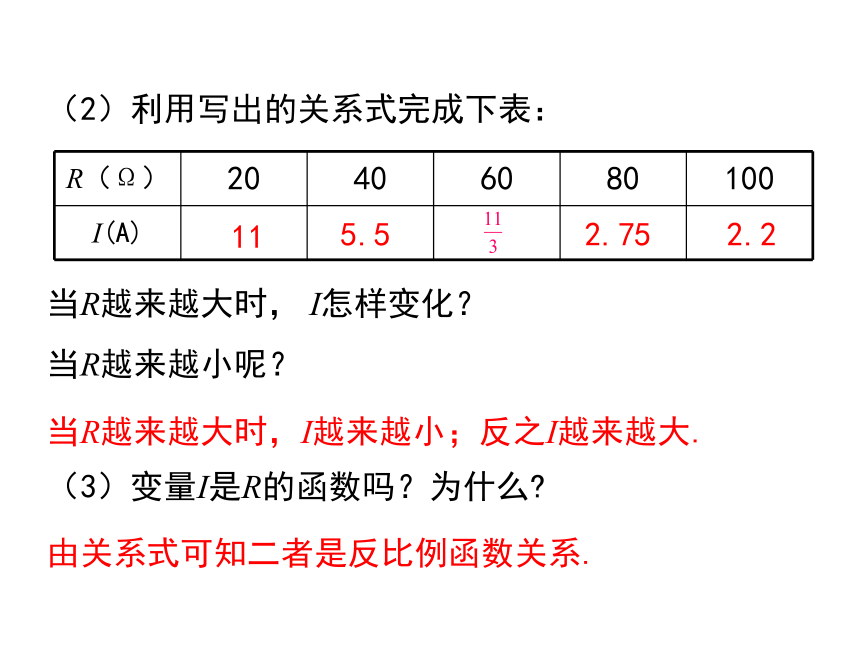
(2)利用写出的关系式完成下表:
R(Ω)
20
40
60
80
100
I(A)
11
5.5
2.75
2.2
1.如果两个变量x、y之间的关系可以表示成________
(k为常数,k≠0)的形式,那么就把y叫做x的反比例函数,其中自变量x的取值范围是_________.
x≠0
2.一般地,反比例函数有以下三种表达式:
(注意
k
≠
0)
练习
(1)京沪铁路全程为1318km,乘坐某次列车所用时间t(单位:h)随该列车平均速度v(单位:km/h)的变化而变化;
(二)合作探究
下列问题中,变量间的对应关系可用怎样的函数关系式表示?这些函数有什么共同特点?
(2)某住宅小区要种值一个面积为1000m2的矩形草坪,草坪的长y随宽x的变化而变化;
(3)已知北京市的总面积为1.68×104平方千米,人均占有土地面积S(单位:平方千米/人)随全市人口n(单位:人)的变化而变化.
解:(1)
(2)
(3)
其中v是自变量,t是v的函数;x是自变量,y是x的函数;n是自变量,S是n的函数.
上面的函数关系式,都具有
的形式,其中k是常
数.
一般地,如果两个变量x,y之间可以表示成
(k为常数且k≠0)的形式,那么称y是x的反比例函数.
归纳结论:
例
已知y是x的反比例函数,当x=2时,y=6.
(1)写出y与x的函数关系式;
(2)求当x=4时,y的值.
分析:因为y是x的反比例函数,所以可设
,
再把x=2和y=6代入上式就可求出常数k的值.
解:(1)设
因为x=2时,y=6,所以有
解得k=12,因此
(2)把x=4代入
练习
1.已知函数
当x=1时,y=-3,那么这个函数
的解析式是( )
A.
B.
C.
D.
B
2.已知y与x成反比,当x=3时,y=4,那么y=3时,x的值等于( )
A.4
B.-4
C.3
D.-3
A
3.若函数y=(m-1)xm2-2是关于x的反比例函数,则m的值______.
4.已知y+1与x成反比例,当y=1时,
(1)求y与x的函数关系式;(2)当x=3时,求y的值.
-1
解:(1)∵y+1与x成反比例,
把
,y=1代入上式中,得
∴k=1,∴y与x的函数关系式为
(2)当x=3时,
1.下面的函数是反比例函数的是( )
A.y=3x+1 B.y=x2+2x
C.
D.
D
课堂练习
2.当路程s一定时,速度v与时间t之间的函数关系是( )
A.正比例函数
B.反比例函数
C.一次函数
D.无法确定
B
3.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为( )
C
4.下列各问题中的两个变量成反比例的是(
)
A.某人的体重与年龄
B.时间不变时,工作量与工作效率
C.矩形的长一定时,它的周长与宽
D.被除数不变时,除数与商
D
5.A、B两地相距120千米,一辆汽车从A地去B地,则其速度v(千米/时)与行驶时间t(小时)之间的函数关系可表示为
.
?
v=
6.有一面积为60的梯形,其上底长是下底长的
,设下底长为x,高为y,则y与x的函数关系式是
;
?
y=
7.某工人承包运输粮食的总数是w吨,每天运x吨,共运了y天,则y与x的关系式为_____,
是______函数.
反比例
8.已知y=y1+y2,且y1与x成正比例,y2与x成反比例,当x=1时,y=4;当x=2时,y=5.
(1)求y与x之间的函数关系式;
(2)求当x=4时,y的值.
建立反比例函数模型
用待定系数法求反比例函数解析式
反比例函数:定义/三种表达方式
反比例函数
总结新知
再
见
北师大版数学九年级上册
第六章
反比例函数
6.1
反比例函数
1.领会反比例函数的意义,理解反比例函数的概念,了解反比例函数三种表达式.
2.能根据现实情境确定反比例函数的解析式.
学习目标
我们在前面学过一次函数和正比例函数,知道一次函数的表达式为y=kx+b(其中k,b为常数且k≠0),正比例函数的表达式为y=kx(k为常数且k≠0),在现实生活中,并不是只有这两种类型的表达式,如从A到B地的路程为1200km,某人开车从A地到B地,汽车的速度v(km/h)和时间t(h)之间的关系式为vt=1200,则
中,t和v之间肯定不是正比例函数和一次函数关系,那么它们之间究竟是什么关系呢?这就是本节课我们要揭开的奥秘.
回顾旧知
知识模块 反比例函数的概念及应用
(一)自主探究
电流I,电压U,电阻R之间满足关系式
.当U=220V时,
(1)你能用含R的代数式表示I吗?
U=IR
探究新知
当R越来越大时,
I怎样变化?
当R越来越小呢?
(3)变量I是R的函数吗?为什么?
当R越来越大时,I越来越小;反之I越来越大.
由关系式可知二者是反比例函数关系.
(2)利用写出的关系式完成下表:
R(Ω)
20
40
60
80
100
I(A)
11
5.5
2.75
2.2
1.如果两个变量x、y之间的关系可以表示成________
(k为常数,k≠0)的形式,那么就把y叫做x的反比例函数,其中自变量x的取值范围是_________.
x≠0
2.一般地,反比例函数有以下三种表达式:
(注意
k
≠
0)
练习
(1)京沪铁路全程为1318km,乘坐某次列车所用时间t(单位:h)随该列车平均速度v(单位:km/h)的变化而变化;
(二)合作探究
下列问题中,变量间的对应关系可用怎样的函数关系式表示?这些函数有什么共同特点?
(2)某住宅小区要种值一个面积为1000m2的矩形草坪,草坪的长y随宽x的变化而变化;
(3)已知北京市的总面积为1.68×104平方千米,人均占有土地面积S(单位:平方千米/人)随全市人口n(单位:人)的变化而变化.
解:(1)
(2)
(3)
其中v是自变量,t是v的函数;x是自变量,y是x的函数;n是自变量,S是n的函数.
上面的函数关系式,都具有
的形式,其中k是常
数.
一般地,如果两个变量x,y之间可以表示成
(k为常数且k≠0)的形式,那么称y是x的反比例函数.
归纳结论:
例
已知y是x的反比例函数,当x=2时,y=6.
(1)写出y与x的函数关系式;
(2)求当x=4时,y的值.
分析:因为y是x的反比例函数,所以可设
,
再把x=2和y=6代入上式就可求出常数k的值.
解:(1)设
因为x=2时,y=6,所以有
解得k=12,因此
(2)把x=4代入
练习
1.已知函数
当x=1时,y=-3,那么这个函数
的解析式是( )
A.
B.
C.
D.
B
2.已知y与x成反比,当x=3时,y=4,那么y=3时,x的值等于( )
A.4
B.-4
C.3
D.-3
A
3.若函数y=(m-1)xm2-2是关于x的反比例函数,则m的值______.
4.已知y+1与x成反比例,当y=1时,
(1)求y与x的函数关系式;(2)当x=3时,求y的值.
-1
解:(1)∵y+1与x成反比例,
把
,y=1代入上式中,得
∴k=1,∴y与x的函数关系式为
(2)当x=3时,
1.下面的函数是反比例函数的是( )
A.y=3x+1 B.y=x2+2x
C.
D.
D
课堂练习
2.当路程s一定时,速度v与时间t之间的函数关系是( )
A.正比例函数
B.反比例函数
C.一次函数
D.无法确定
B
3.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为( )
C
4.下列各问题中的两个变量成反比例的是(
)
A.某人的体重与年龄
B.时间不变时,工作量与工作效率
C.矩形的长一定时,它的周长与宽
D.被除数不变时,除数与商
D
5.A、B两地相距120千米,一辆汽车从A地去B地,则其速度v(千米/时)与行驶时间t(小时)之间的函数关系可表示为
.
?
v=
6.有一面积为60的梯形,其上底长是下底长的
,设下底长为x,高为y,则y与x的函数关系式是
;
?
y=
7.某工人承包运输粮食的总数是w吨,每天运x吨,共运了y天,则y与x的关系式为_____,
是______函数.
反比例
8.已知y=y1+y2,且y1与x成正比例,y2与x成反比例,当x=1时,y=4;当x=2时,y=5.
(1)求y与x之间的函数关系式;
(2)求当x=4时,y的值.
建立反比例函数模型
用待定系数法求反比例函数解析式
反比例函数:定义/三种表达方式
反比例函数
总结新知
再
见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
