沪科版七年级上册数学:1.6 有理数的乘方 课件 共24张PPT)
文档属性
| 名称 | 沪科版七年级上册数学:1.6 有理数的乘方 课件 共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 522.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
1.6
有理数的乘方
返回
下一张
上一张
退出
他是中世纪意大利的数学家,是黄金分割数列的发明者,著有《算盘全书》、《计算之书》,猜一猜他是谁?
斐波那契
)
祝你成功
中世纪意大利数学家斐波那契在《算盘全书》里记载了一首歌谣:
我赴圣地爱弗西,途遇妇女数有七,一人七袋手中提,一袋七猫数整齐,一猫七子紧相依,妇与布袋猫与子,几何同时赴圣地?
祝你成功
妇女:
7
=
动动脑
71
布袋:
7X7=
子:
7X7X7X7
=
72
73
猫:
7X7X7=
74
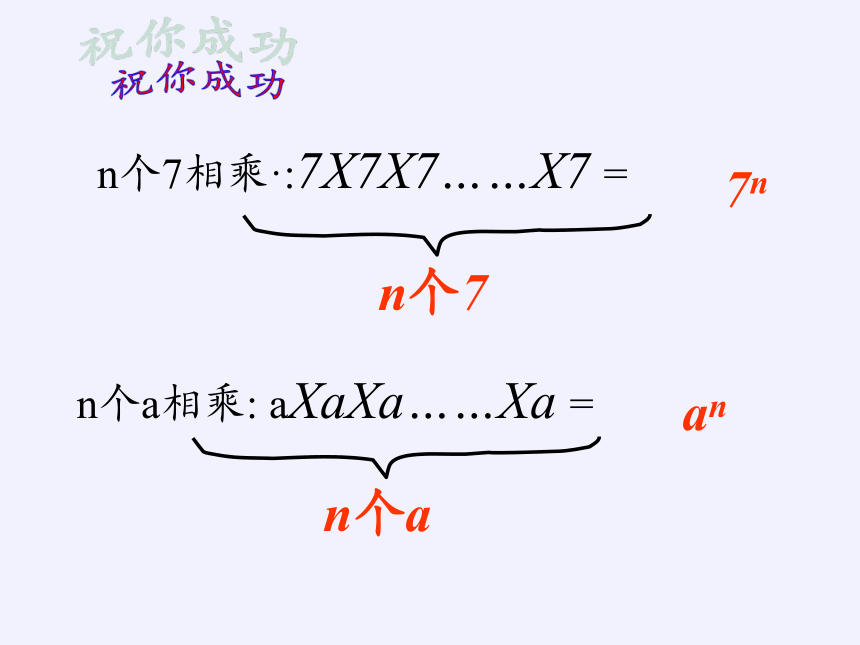
n个7相乘·:7X7X7……X7
=
n个7
7n
n个a相乘:
aXaXa……Xa
=
an
n个a
祝你成功
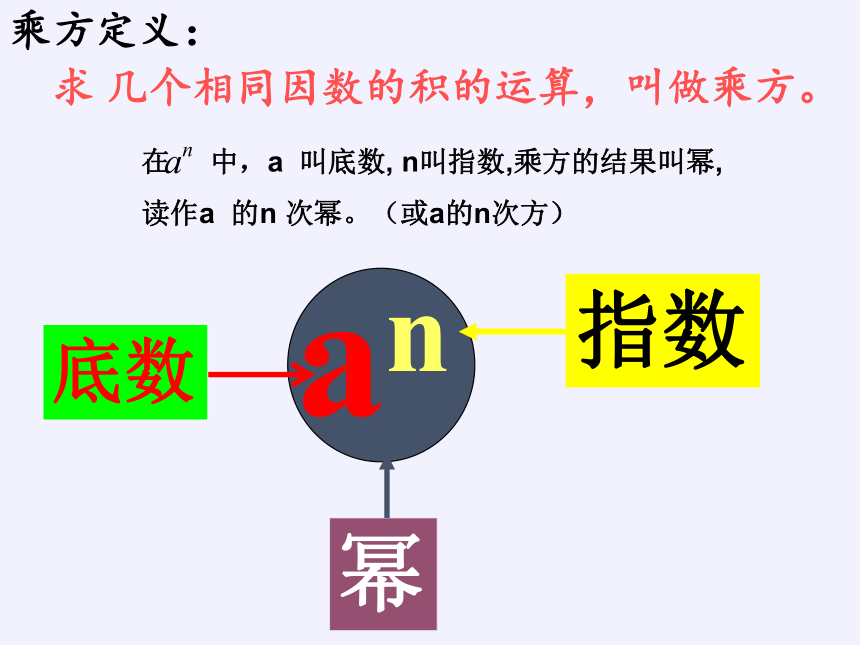
乘方定义:
an
底数
指数
幂
求
几个相同因数的积的运算,叫做乘方。
在
中,a
叫底数,
n叫指数,乘方的结果叫幂,
读作a
的n
次幂。(或a的n次方)
其中a代表相乘的因数,n代表
相乘因数的个数即:
a×a×a···×a
n个a
an
=
乘方的意义
也就是a的n次方等于n个a相乘
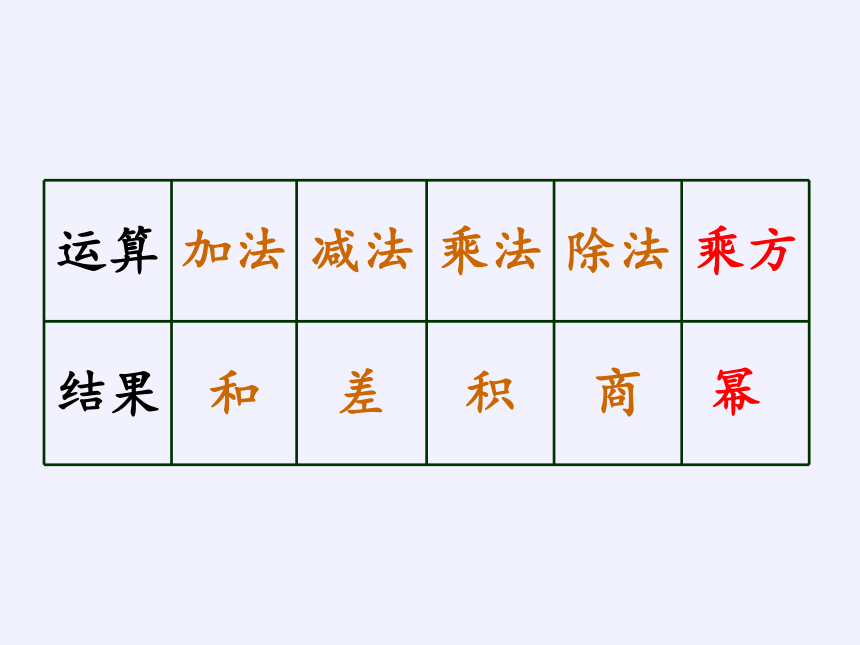
运算
加法
减法
乘法
除法
乘方
结果
和
差
积
商
幂
(1)在(-6)4中,底数是
___,
指数是___;
-6
4
祝你成功
(3)
的底数是
,指数是
读作
;
7
的7次方
(4)在
中,-3是
数,16是
数,读作
。
底
指
-3的16次方
(2)在
(-a)5
中,底数是
指数是
;
5
-a
练一练
5)5看成幂的话,底数是
,指数是
,可读作
;
6)
看成幂的话,底数是
,指数是
,可读作
;
幂
指数
底数
5
1
5的一次方
1
的一次方
幂
指数
底数
注意:
一个数可以看作这个数本身的一次方,
如
5
就是
,但通常幂指数为1时省略不写。
5
1
注意:在书写分数、负数的乘方时一定要把整个分数、负数(连同符号),用小括号括起来。
把下列相同的因数写成幂的形式。
自我探究
1
2
(
)
3
如:
、(-3)2
写法
读法
底数
意义
结果
有括号
无括号
负
3
的
3
次方
3
的
3次方的相反数
-3
3
3个-3相乘
3个3连乘积的相反数
-27
-27
辨一辨
例1
计算:
(1)
(2)
(3)
(1)
(2)
(3)
解:
题目
底数的符号
指数的奇、偶
幂的符号
32
(-3)4
53
(-2)6
(-3)3
(-4)5
+
偶数
+
+
奇数
+
-
偶数
+
-
偶数
+
-
奇数
-
-
奇数
-
填表:你能发现乘方运算符号有什么规律吗?
探究法则
正数的任何次幂都是正数;
乘方的符号法则:
合作探究
负数的奇次幂是负数,
负数的偶次幂是正数。
你能迅速确定下列幂的正负吗?
+
+
+
-
用一用
游戏:找朋友,结果相等的站在一起
-(-4)3
,
34,
0.252,
(-4)3,
(-0.25)2,-43,
82
,(-3)4
返回
下一张
上一张
退出
珠穆朗玛峰是世界的最高峰,
它的海拔高度是8844米。把一张
足够大的厚度为0.1毫米的纸,
连续对折30次的厚度能超过珠穆
朗玛峰。这是真的吗?
这张纸对折30次后能超过珠穆朗玛峰吗?
如果把足够长的厚0.1毫米的纸折叠30次后有10万多米高,有12个珠穆朗玛峰高。
分析:
0.1毫米×230=0.1毫米×1073741824
=107374.1824米
8844.43
×12=106133.16
这下你该
相信了吧!
小结:
你能告诉我这节课的收获吗?
乘方运算的法则:
正数的任何次幂都是正数;
0的任何正整数次幂都是0;负数的奇次幂是负数,负数的偶次幂是正数
乘方:求几个相同因数的积的运算,叫做乘方
一分耕耘,一分收获!
通过这节课的学习,你有什么体会?
反思
“乘方”精神:乘方虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。加油吧!同学们!
布置作业
教科书第41页练习第2、3、4题。
祝同学们学习进步!
谢
谢
1.6
有理数的乘方
返回
下一张
上一张
退出
他是中世纪意大利的数学家,是黄金分割数列的发明者,著有《算盘全书》、《计算之书》,猜一猜他是谁?
斐波那契
)
祝你成功
中世纪意大利数学家斐波那契在《算盘全书》里记载了一首歌谣:
我赴圣地爱弗西,途遇妇女数有七,一人七袋手中提,一袋七猫数整齐,一猫七子紧相依,妇与布袋猫与子,几何同时赴圣地?
祝你成功
妇女:
7
=
动动脑
71
布袋:
7X7=
子:
7X7X7X7
=
72
73
猫:
7X7X7=
74
n个7相乘·:7X7X7……X7
=
n个7
7n
n个a相乘:
aXaXa……Xa
=
an
n个a
祝你成功
乘方定义:
an
底数
指数
幂
求
几个相同因数的积的运算,叫做乘方。
在
中,a
叫底数,
n叫指数,乘方的结果叫幂,
读作a
的n
次幂。(或a的n次方)
其中a代表相乘的因数,n代表
相乘因数的个数即:
a×a×a···×a
n个a
an
=
乘方的意义
也就是a的n次方等于n个a相乘
运算
加法
减法
乘法
除法
乘方
结果
和
差
积
商
幂
(1)在(-6)4中,底数是
___,
指数是___;
-6
4
祝你成功
(3)
的底数是
,指数是
读作
;
7
的7次方
(4)在
中,-3是
数,16是
数,读作
。
底
指
-3的16次方
(2)在
(-a)5
中,底数是
指数是
;
5
-a
练一练
5)5看成幂的话,底数是
,指数是
,可读作
;
6)
看成幂的话,底数是
,指数是
,可读作
;
幂
指数
底数
5
1
5的一次方
1
的一次方
幂
指数
底数
注意:
一个数可以看作这个数本身的一次方,
如
5
就是
,但通常幂指数为1时省略不写。
5
1
注意:在书写分数、负数的乘方时一定要把整个分数、负数(连同符号),用小括号括起来。
把下列相同的因数写成幂的形式。
自我探究
1
2
(
)
3
如:
、(-3)2
写法
读法
底数
意义
结果
有括号
无括号
负
3
的
3
次方
3
的
3次方的相反数
-3
3
3个-3相乘
3个3连乘积的相反数
-27
-27
辨一辨
例1
计算:
(1)
(2)
(3)
(1)
(2)
(3)
解:
题目
底数的符号
指数的奇、偶
幂的符号
32
(-3)4
53
(-2)6
(-3)3
(-4)5
+
偶数
+
+
奇数
+
-
偶数
+
-
偶数
+
-
奇数
-
-
奇数
-
填表:你能发现乘方运算符号有什么规律吗?
探究法则
正数的任何次幂都是正数;
乘方的符号法则:
合作探究
负数的奇次幂是负数,
负数的偶次幂是正数。
你能迅速确定下列幂的正负吗?
+
+
+
-
用一用
游戏:找朋友,结果相等的站在一起
-(-4)3
,
34,
0.252,
(-4)3,
(-0.25)2,-43,
82
,(-3)4
返回
下一张
上一张
退出
珠穆朗玛峰是世界的最高峰,
它的海拔高度是8844米。把一张
足够大的厚度为0.1毫米的纸,
连续对折30次的厚度能超过珠穆
朗玛峰。这是真的吗?
这张纸对折30次后能超过珠穆朗玛峰吗?
如果把足够长的厚0.1毫米的纸折叠30次后有10万多米高,有12个珠穆朗玛峰高。
分析:
0.1毫米×230=0.1毫米×1073741824
=107374.1824米
8844.43
×12=106133.16
这下你该
相信了吧!
小结:
你能告诉我这节课的收获吗?
乘方运算的法则:
正数的任何次幂都是正数;
0的任何正整数次幂都是0;负数的奇次幂是负数,负数的偶次幂是正数
乘方:求几个相同因数的积的运算,叫做乘方
一分耕耘,一分收获!
通过这节课的学习,你有什么体会?
反思
“乘方”精神:乘方虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。加油吧!同学们!
布置作业
教科书第41页练习第2、3、4题。
祝同学们学习进步!
谢
谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
