人教版数学八年级上册13.3.1等腰三角形性质及判定(基础+提高)同步检测(Word版 含答案)
文档属性
| 名称 | 人教版数学八年级上册13.3.1等腰三角形性质及判定(基础+提高)同步检测(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 321.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 00:00:00 | ||
图片预览



文档简介
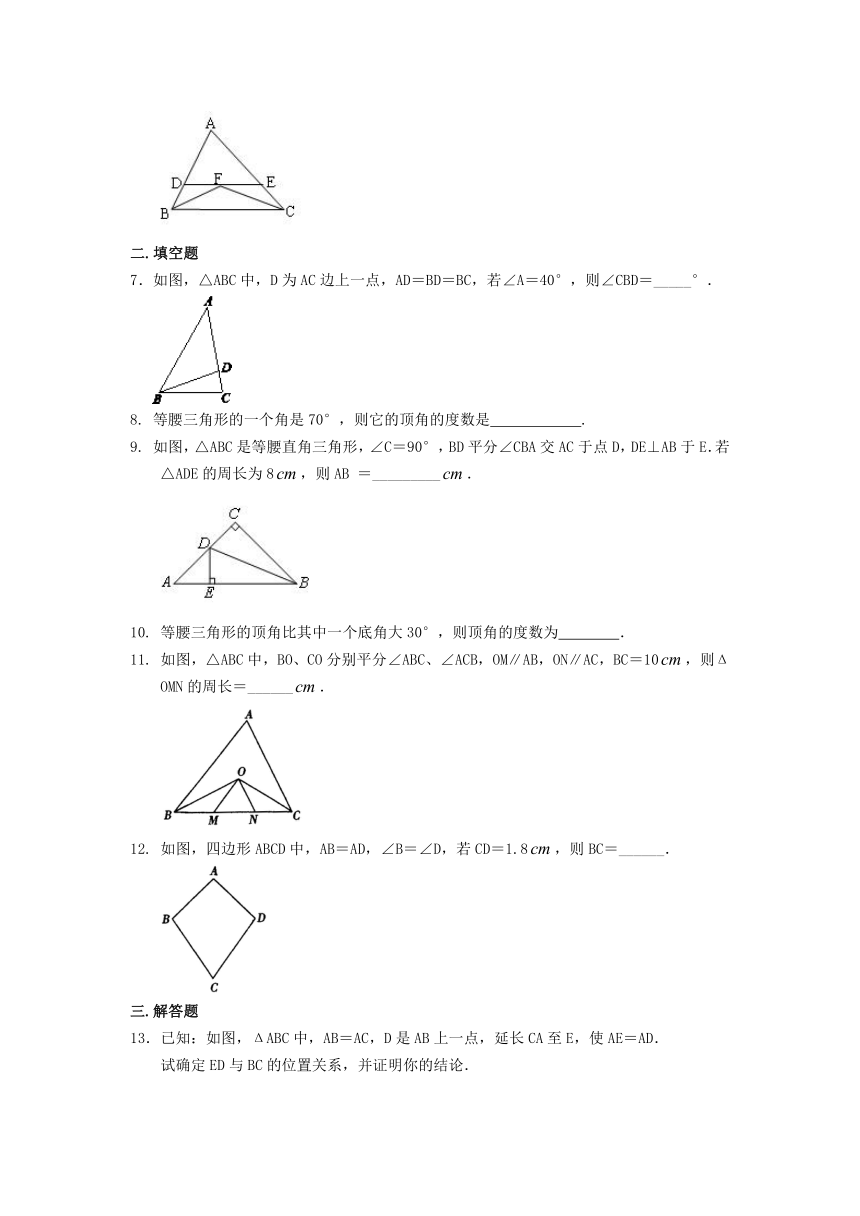
基础篇
一.选择题
1.
已知一个等腰三角形两边长分别为7,9,则它的周长为(
)
A.23
B.25
C.23或25
D.14或18
2.
若一个三角形的三个外角度数比为2:3:3,则这个三角形是(
)
A.
直角三角形
B.
等边三角形
C.
等腰三角形
D.
等腰直角三角形
3.
将两个全等的且有一个角为30°的直角三角形拼成如图所示形状,两条长直角边在同一条直线上,则图中等腰三角形的个数是(
)
A.
4个
B.
3个
C.
2个
D.
1个
如图,ΔABC中,AB=AC,∠BAC=108°,若AD、AE三等分∠BAC,则图中等腰三角形有
(
)
A.4个
B.5个
C.6个
D.7个
5.
如图,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若,则度数是(
)
A.60°
B.70°
C.80°
D.不确定
如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的有(
)
①△BDF,△CEF都是等腰三角形;
②DE=DB+CE;
③AD+DE+AE=AB+AC;
④BF=CF.
A.1个
B.2个
C.3个
D.4个
二.填空题
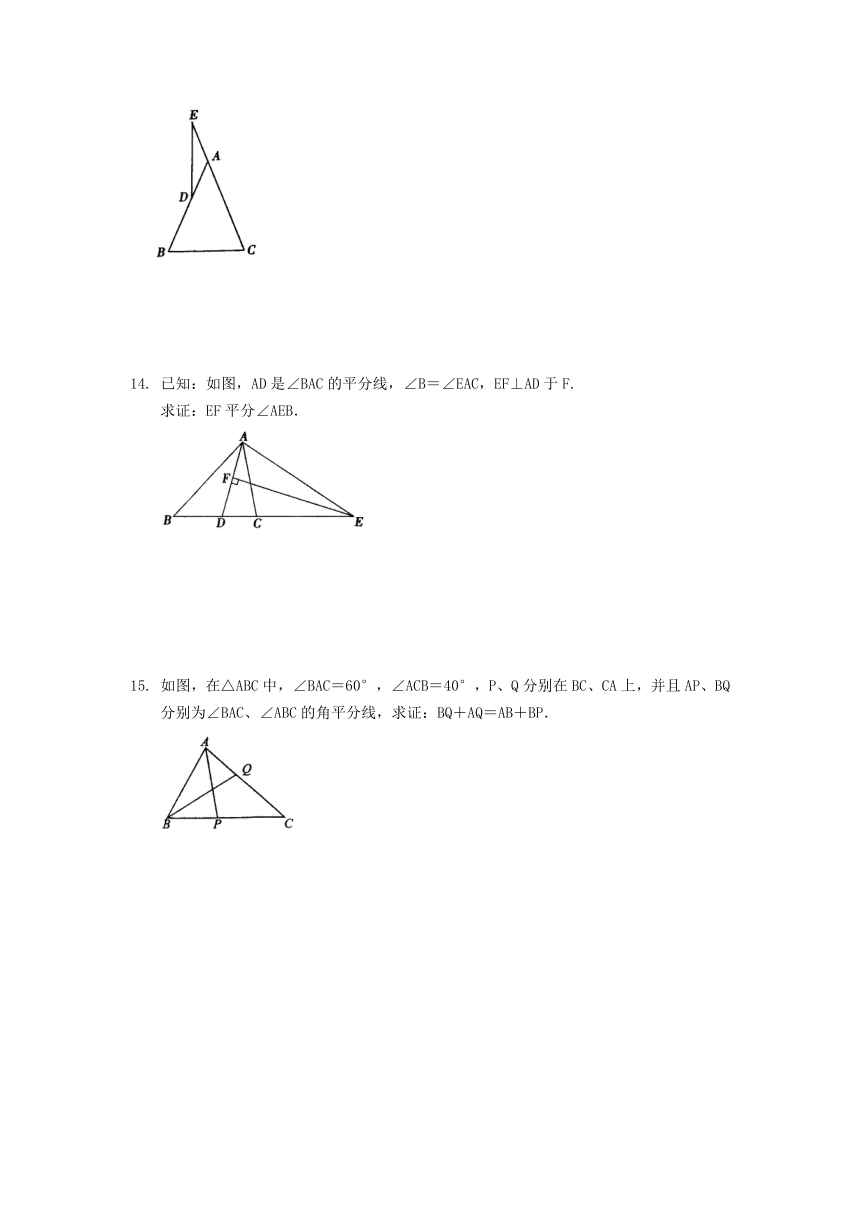
7.如图,△ABC中,D为AC边上一点,AD=BD=BC,若∠A=40°,则∠CBD=_____°.
8.
等腰三角形的一个角是70°,则它的顶角的度数是
.
9.
如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8,则AB
=_________.
10.
等腰三角形的顶角比其中一个底角大30°,则顶角的度数为
.
11.
如图,△ABC中,BO、CO分别平分∠ABC、∠ACB,OM∥AB,ON∥AC,BC=10,则ΔOMN的周长=______.
12.
如图,四边形ABCD中,AB=AD,∠B=∠D,若CD=1.8,则BC=______.
三.解答题
13.已知:如图,ΔABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.
试确定ED与BC的位置关系,并证明你的结论.
14.
已知:如图,AD是∠BAC的平分线,∠B=∠EAC,EF⊥AD于F.
求证:EF平分∠AEB.
15.
如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、CA上,并且AP、BQ分别为∠BAC、∠ABC的角平分线,求证:BQ+AQ=AB+BP.
提高篇
一.选择题
1.如图,在△ABC中,若AB=AC,BC=BD,AD=DE=EB,则∠A等于(
).
A.30°
B.36°
C.45°
D.54°
2.
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为(
).
A.1
B.1.5
C.2
D.2.5
3.
如图,ΔABC中,AB=AC,BE=CD,BD=CF,则∠EDF=
(
)
A.2∠A
B.90°-2∠A
C.90°-∠A
D.
4.
等腰三角形两边、满足||+=0,则此三角形的周长是(
)
A.7
B.5
C.8
D.7或5
5.如图所示,在长方形ABCD的对称轴上找点P,使得△PAB、△PBC均为等腰三角形,则满足条件的点P有(
)
A.1个
B.3个
C.5个
D.无数多个
6.
如图所示,矩形ABCD中,AB=4,BC=,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点、在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
A、2个
B、3个
C、4个
D、5个
二.填空题
7.已知一个等腰三角形的顶角为度,则其一腰上的高线与底边的夹角___________度(用含的式子表示).
8.
已知等腰三角形的两边长分别为2和3,则其周长为________.
9.
等腰三角形的周长为22,其中一边的长是8,则其余两边长分别为________.
10.
如图,在ΔABC中,高AD、BE交于H点,若BH=AC,则∠ABC=______°.
11.如图,钝角三角形纸片ABC中,∠BAC=110°,D为AC边的中点.现将纸片沿过点D的直线折叠,折痕与BC交于点E,点C的落点记为F.若点F恰好在BA的延长线上,则∠ADF
=_________°.
12.
如图,在ΔABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为______°.
三.解答题
13.
已知,如图,在△ABC中,BE是角平分线,AD⊥BE垂足为D,
求证:∠BAD=∠DAE+∠C
14.已知,如图,△ABC中,D是BC中点,DE⊥DF,
试判断BE+CF与EF的大小关系,并证明你的结论.
15.在中,,点是直线上一点(不与重合),以AD
为一边在AD
的右侧作,使,连接.
(1)如图1,当点在线段上,如果,则_________;
(2)设,.
①如图2,当点在线段上移动,则之间有怎样的数量关系?请说明理由;
②当点在直线上移动,则之间有怎样的数量关系?请直接写出你的结论.
答案
基础篇
一.选择题
1.
C;
2.
D;
3.
B;
4.
C;
5.
C;
6.
C;
二.填空题
7.
20;
8.
70°或40o;
9.
8;
10.80°;
11.10;
12.1.8;
三.解答题
13.【解析】
证明:ED⊥BC;延长ED,交BC边于H,
∵AB=AC,AE=AD.
∴设∠B=∠C=,则∠EAD=2,
∴∠ADE=
即∠BDH=90°-
∴∠B+∠BDH=+90°-=90°,
∴∠BHD=90°,ED⊥BC.
14.【解析】
证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD
又∵∠B=∠EAC,
∴∠B+∠BAD=∠EAC+∠CAD,即∠ADE=∠DAE
∵EF⊥AD,
∴∠AFE=∠DFE
在Rt△AEF和Rt△DEF中
∴Rt△AEF≌Rt△DEF(AAS)
∴∠AEF=∠DEF,即EF平分∠AEB.
15.【解析】
证明:延长AB至E,使BE=BP,连接EP
∵在△ABC中,∠BAC=60°,∠ACB=40°,
∴∠ABC=80°
∴∠E=∠BPE==40°
∵AP、BQ分别为∠BAC、∠ABC的角平分线,
∴∠QBC=40°,∠BAP=∠CAP
∴BQ=QC(等角对等边)
在△AEP与△ACP中,
∴△AEP≌△ACP(AAS)
∴AE=AC
∴AB+BE=AQ+QC,即AB+BP=AQ+BQ.
提高篇
一.选择题
1.
C;
2.
A;
3.
D;
4.
A;
5.
C;
6.
C;
二.填空题
7.
;
8.
7或8;
9.
7,7或8,6;
10.45;
11.40;
12.15°;
三.解答题
13.【解析】
证明:延长AD交BC于F
∵BE平分∠ABC,
∴∠ABE=∠CBE
∵AD⊥BD
∴∠ADB=∠BDF=90?
在△ABD与△FBD中
∴△ABD≌△FBD
(ASA)
∴BA=BF
∴∠BAD=∠BFA
∴∠BFA=∠DAE+∠C
∴∠BAD=∠DAE+∠C
14.【解析】BE+CF>EF
证明:延长FD到G,使DG=DF,连结BG、EG
∵D是BC中点
∴BD=CD
又∵DE⊥DF
∴EG=EF
在△FDC与△GDB中
∴△FDC≌△GDB(SAS)
∴BG=CF
∵BG+BE>EG
∴BE+CF>EF.
15.【解析】(1)90°;
(2)①α+β=180°.
证明:①∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
∴△ABD≌△ACE,
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,
∴α+β=180°;
②如图:当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β.
一.选择题
1.
已知一个等腰三角形两边长分别为7,9,则它的周长为(
)
A.23
B.25
C.23或25
D.14或18
2.
若一个三角形的三个外角度数比为2:3:3,则这个三角形是(
)
A.
直角三角形
B.
等边三角形
C.
等腰三角形
D.
等腰直角三角形
3.
将两个全等的且有一个角为30°的直角三角形拼成如图所示形状,两条长直角边在同一条直线上,则图中等腰三角形的个数是(
)
A.
4个
B.
3个
C.
2个
D.
1个
如图,ΔABC中,AB=AC,∠BAC=108°,若AD、AE三等分∠BAC,则图中等腰三角形有
(
)
A.4个
B.5个
C.6个
D.7个
5.
如图,D是AB边上的中点,将沿过D的直线折叠,使点A落在BC上F处,若,则度数是(
)
A.60°
B.70°
C.80°
D.不确定
如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的有(
)
①△BDF,△CEF都是等腰三角形;
②DE=DB+CE;
③AD+DE+AE=AB+AC;
④BF=CF.
A.1个
B.2个
C.3个
D.4个
二.填空题
7.如图,△ABC中,D为AC边上一点,AD=BD=BC,若∠A=40°,则∠CBD=_____°.
8.
等腰三角形的一个角是70°,则它的顶角的度数是
.
9.
如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8,则AB
=_________.
10.
等腰三角形的顶角比其中一个底角大30°,则顶角的度数为
.
11.
如图,△ABC中,BO、CO分别平分∠ABC、∠ACB,OM∥AB,ON∥AC,BC=10,则ΔOMN的周长=______.
12.
如图,四边形ABCD中,AB=AD,∠B=∠D,若CD=1.8,则BC=______.
三.解答题
13.已知:如图,ΔABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.
试确定ED与BC的位置关系,并证明你的结论.
14.
已知:如图,AD是∠BAC的平分线,∠B=∠EAC,EF⊥AD于F.
求证:EF平分∠AEB.
15.
如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、CA上,并且AP、BQ分别为∠BAC、∠ABC的角平分线,求证:BQ+AQ=AB+BP.
提高篇
一.选择题
1.如图,在△ABC中,若AB=AC,BC=BD,AD=DE=EB,则∠A等于(
).
A.30°
B.36°
C.45°
D.54°
2.
如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为(
).
A.1
B.1.5
C.2
D.2.5
3.
如图,ΔABC中,AB=AC,BE=CD,BD=CF,则∠EDF=
(
)
A.2∠A
B.90°-2∠A
C.90°-∠A
D.
4.
等腰三角形两边、满足||+=0,则此三角形的周长是(
)
A.7
B.5
C.8
D.7或5
5.如图所示,在长方形ABCD的对称轴上找点P,使得△PAB、△PBC均为等腰三角形,则满足条件的点P有(
)
A.1个
B.3个
C.5个
D.无数多个
6.
如图所示,矩形ABCD中,AB=4,BC=,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点、在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
A、2个
B、3个
C、4个
D、5个
二.填空题
7.已知一个等腰三角形的顶角为度,则其一腰上的高线与底边的夹角___________度(用含的式子表示).
8.
已知等腰三角形的两边长分别为2和3,则其周长为________.
9.
等腰三角形的周长为22,其中一边的长是8,则其余两边长分别为________.
10.
如图,在ΔABC中,高AD、BE交于H点,若BH=AC,则∠ABC=______°.
11.如图,钝角三角形纸片ABC中,∠BAC=110°,D为AC边的中点.现将纸片沿过点D的直线折叠,折痕与BC交于点E,点C的落点记为F.若点F恰好在BA的延长线上,则∠ADF
=_________°.
12.
如图,在ΔABC中,∠ABC=120°,点D、E分别在AC和AB上,且AE=ED=DB=BC,则∠A的度数为______°.
三.解答题
13.
已知,如图,在△ABC中,BE是角平分线,AD⊥BE垂足为D,
求证:∠BAD=∠DAE+∠C
14.已知,如图,△ABC中,D是BC中点,DE⊥DF,
试判断BE+CF与EF的大小关系,并证明你的结论.
15.在中,,点是直线上一点(不与重合),以AD
为一边在AD
的右侧作,使,连接.
(1)如图1,当点在线段上,如果,则_________;
(2)设,.
①如图2,当点在线段上移动,则之间有怎样的数量关系?请说明理由;
②当点在直线上移动,则之间有怎样的数量关系?请直接写出你的结论.
答案
基础篇
一.选择题
1.
C;
2.
D;
3.
B;
4.
C;
5.
C;
6.
C;
二.填空题
7.
20;
8.
70°或40o;
9.
8;
10.80°;
11.10;
12.1.8;
三.解答题
13.【解析】
证明:ED⊥BC;延长ED,交BC边于H,
∵AB=AC,AE=AD.
∴设∠B=∠C=,则∠EAD=2,
∴∠ADE=
即∠BDH=90°-
∴∠B+∠BDH=+90°-=90°,
∴∠BHD=90°,ED⊥BC.
14.【解析】
证明:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD
又∵∠B=∠EAC,
∴∠B+∠BAD=∠EAC+∠CAD,即∠ADE=∠DAE
∵EF⊥AD,
∴∠AFE=∠DFE
在Rt△AEF和Rt△DEF中
∴Rt△AEF≌Rt△DEF(AAS)
∴∠AEF=∠DEF,即EF平分∠AEB.
15.【解析】
证明:延长AB至E,使BE=BP,连接EP
∵在△ABC中,∠BAC=60°,∠ACB=40°,
∴∠ABC=80°
∴∠E=∠BPE==40°
∵AP、BQ分别为∠BAC、∠ABC的角平分线,
∴∠QBC=40°,∠BAP=∠CAP
∴BQ=QC(等角对等边)
在△AEP与△ACP中,
∴△AEP≌△ACP(AAS)
∴AE=AC
∴AB+BE=AQ+QC,即AB+BP=AQ+BQ.
提高篇
一.选择题
1.
C;
2.
A;
3.
D;
4.
A;
5.
C;
6.
C;
二.填空题
7.
;
8.
7或8;
9.
7,7或8,6;
10.45;
11.40;
12.15°;
三.解答题
13.【解析】
证明:延长AD交BC于F
∵BE平分∠ABC,
∴∠ABE=∠CBE
∵AD⊥BD
∴∠ADB=∠BDF=90?
在△ABD与△FBD中
∴△ABD≌△FBD
(ASA)
∴BA=BF
∴∠BAD=∠BFA
∴∠BFA=∠DAE+∠C
∴∠BAD=∠DAE+∠C
14.【解析】BE+CF>EF
证明:延长FD到G,使DG=DF,连结BG、EG
∵D是BC中点
∴BD=CD
又∵DE⊥DF
∴EG=EF
在△FDC与△GDB中
∴△FDC≌△GDB(SAS)
∴BG=CF
∵BG+BE>EG
∴BE+CF>EF.
15.【解析】(1)90°;
(2)①α+β=180°.
证明:①∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
∴△ABD≌△ACE,
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,
∴α+β=180°;
②如图:当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β.
