人教版九年级上册第二十二章二次函数知识点学案
文档属性
| 名称 | 人教版九年级上册第二十二章二次函数知识点学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 294.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-01 00:00:00 | ||
图片预览


文档简介
人教版九年级上册·第二十二章:二次函数
①二次函数的图像和性质
②二次函数与一元二次方程
③实际问题与二次函数
【考点分析】
1.理解、掌握二次函数的概念和一般形式,根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围
2.确定函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标
3.二次函数y=ax2+bx+c的图象、顶点坐标与对称轴公式.
4.能运用二次函数及其图象确定方程和不等式的解或解集,根据函数图象与x轴的交点情况确定未知字母的值或取值范围.
5.运用二次函数求实际问题中的最大值或最小值.
6.应用二次函数的性质解决图形中最大面积问题.
7.利用二次函数解决拱桥及运动中的有关问题.
【基础知识】
要点一、二次函数的概念
1.二次函数的概念:一般地,形如y=ax2+bx+c(a≠0,a,
b,
c为常数)的函数是二次函数.
若b=0,则y=ax2+c;
若c=0,则y=ax2+bx;
若b=c=0,则y=ax2.
2.二次函数解析式的表示方法
1.
一般式:y=ax2+bx+c(a,b,c,为常数,a≠0)
2.
顶点式:y=a(x-h)2+k(a,h,k,为常数,a≠0)
3.
两根式:y=a(x-x1)(x-x2)(a≠0,x1
x2
是抛物线与x轴两交点的横坐标)或称交点式)
要点二、y=a(x-h)2+k(a,h,k,为常数,a≠0)函数的图象与性质
1.函数y=a(x-h)2+k的图象与性质
a的符号
开口方向
顶点坐标
对称轴
性质
a>0
向上
(h,k)
x=h
x>h时,y随x的增大而增大;xa<0
向下
(h,k)
x=h
x>h时,y随x的增大而减小;x注:
二次函数y=a(x-h)2+k的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
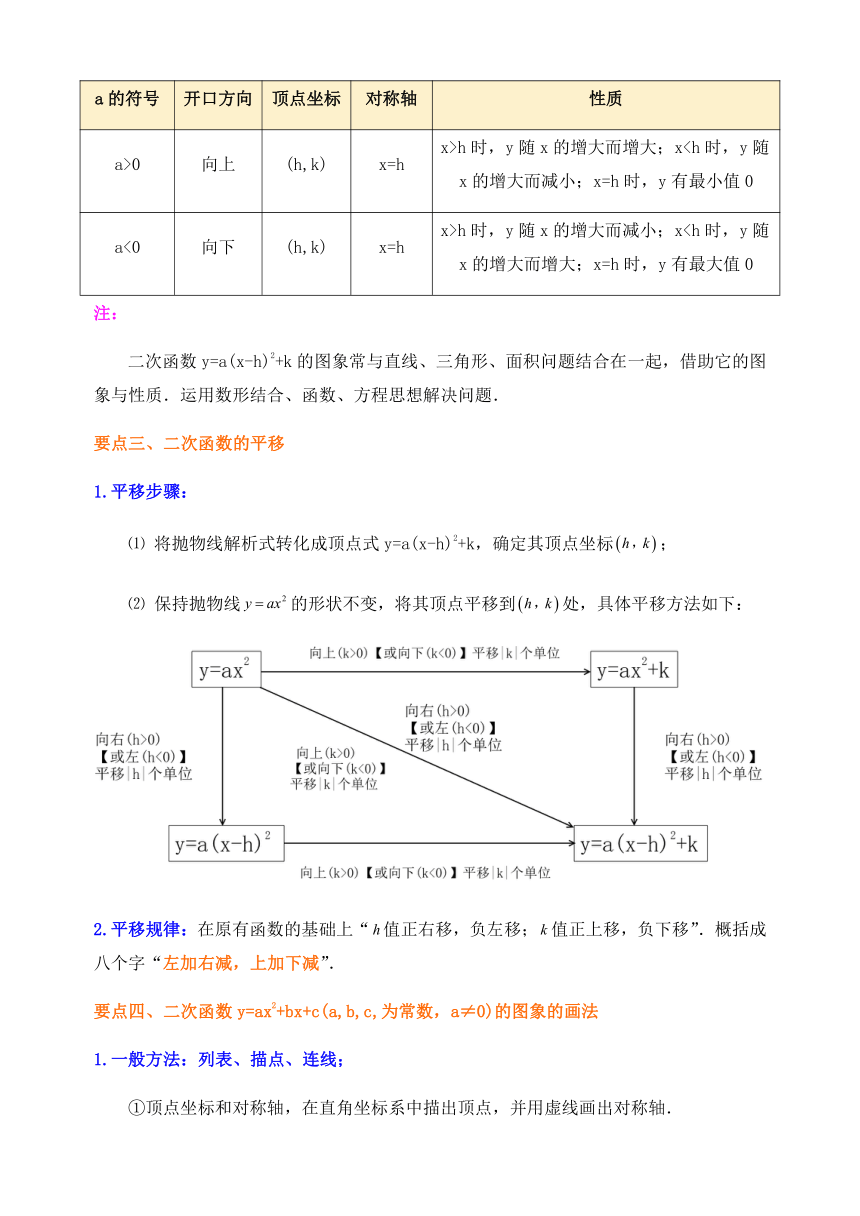
要点三、二次函数的平移
1.平移步骤:
⑴
将抛物线解析式转化成顶点式y=a(x-h)2+k,确定其顶点坐标;
⑵
保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2.平移规律:在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.
要点四、二次函数y=ax2+bx+c(a,b,c,为常数,a≠0)的图象的画法
1.一般方法:列表、描点、连线;
①顶点坐标和对称轴,在直角坐标系中描出顶点,并用虚线画出对称轴.
②求抛物线y=ax2+bx+c与坐标轴的交点,再按顺序用平滑曲线连结起来.
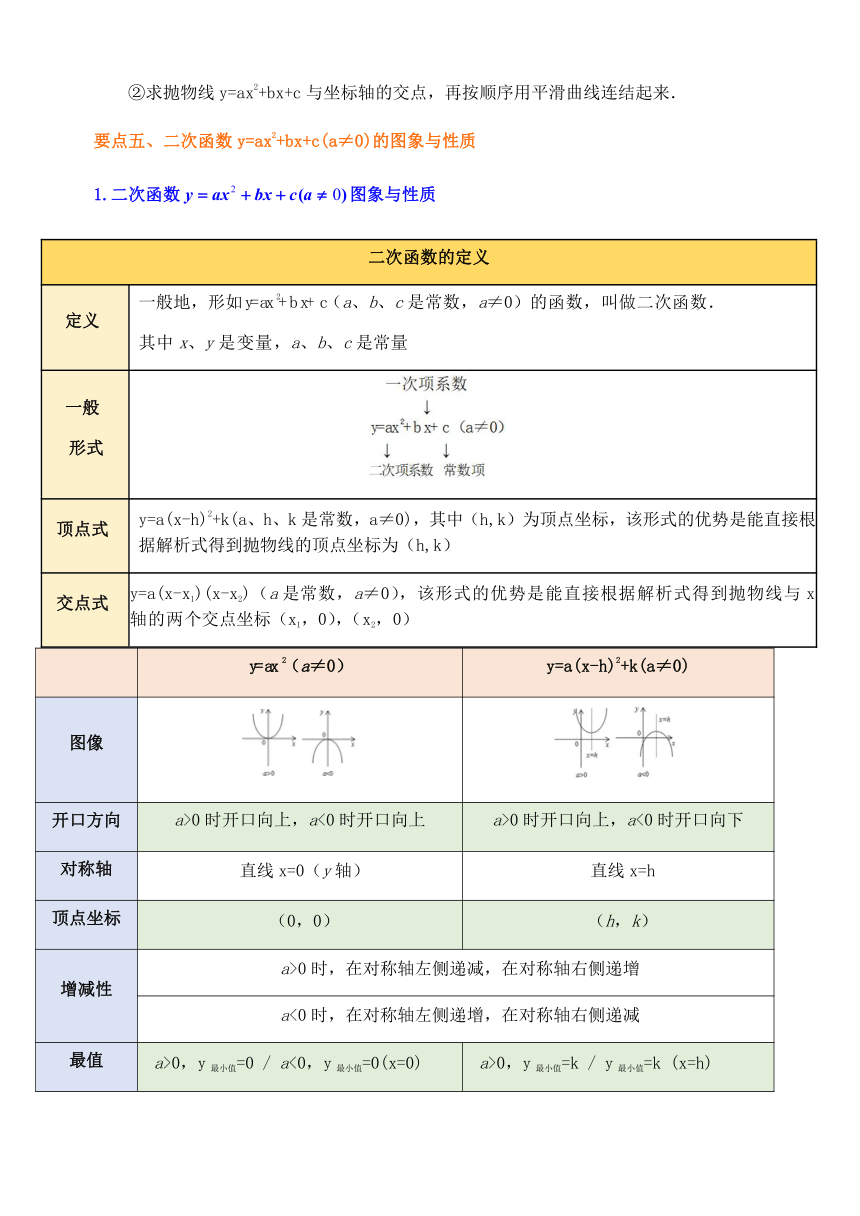
要点五、二次函数y=ax2+bx+c(a≠0)的图象与性质
1.二次函数图象与性质
二次函数的定义
定义
一般地,形如
y=
ax
2
+
b
x+
c(a、b、c是常数,a≠0)的函数,叫做二次函数.
其中x、y是变量,a、b、c是常量
一般
形式
顶点式
y=a(x-h)2+k(a、h、k是常数,a≠0),其中(h,k)为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(h,k)
交点式
y=a(x-x1)(x-x2)(a是常数,a≠0),该形式的优势是能直接根据解析式得到抛物线与x轴的两个交点坐标(x1,0),(
x2,0)
y=
ax
2
(a≠0)
y=a(x-h)2+k(a≠0)
图像
开口方向
a>0时开口向上,a<0时开口向上
a>0时开口向上,a<0时开口向下
对称轴
直线x=0(y轴)
直线x=h
顶点坐标
(0,0)
(h,k)
增减性
a>0时,在对称轴左侧递减,在对称轴右侧递增
a<0时,在对称轴左侧递增,在对称轴右侧递减
最值
a>0,y最小值=0
/
a<0,y最小值=0(x=0)
a>0,y最小值=k
/
y最小值=k
(x=h)
y=
ax
2
+
b
x+
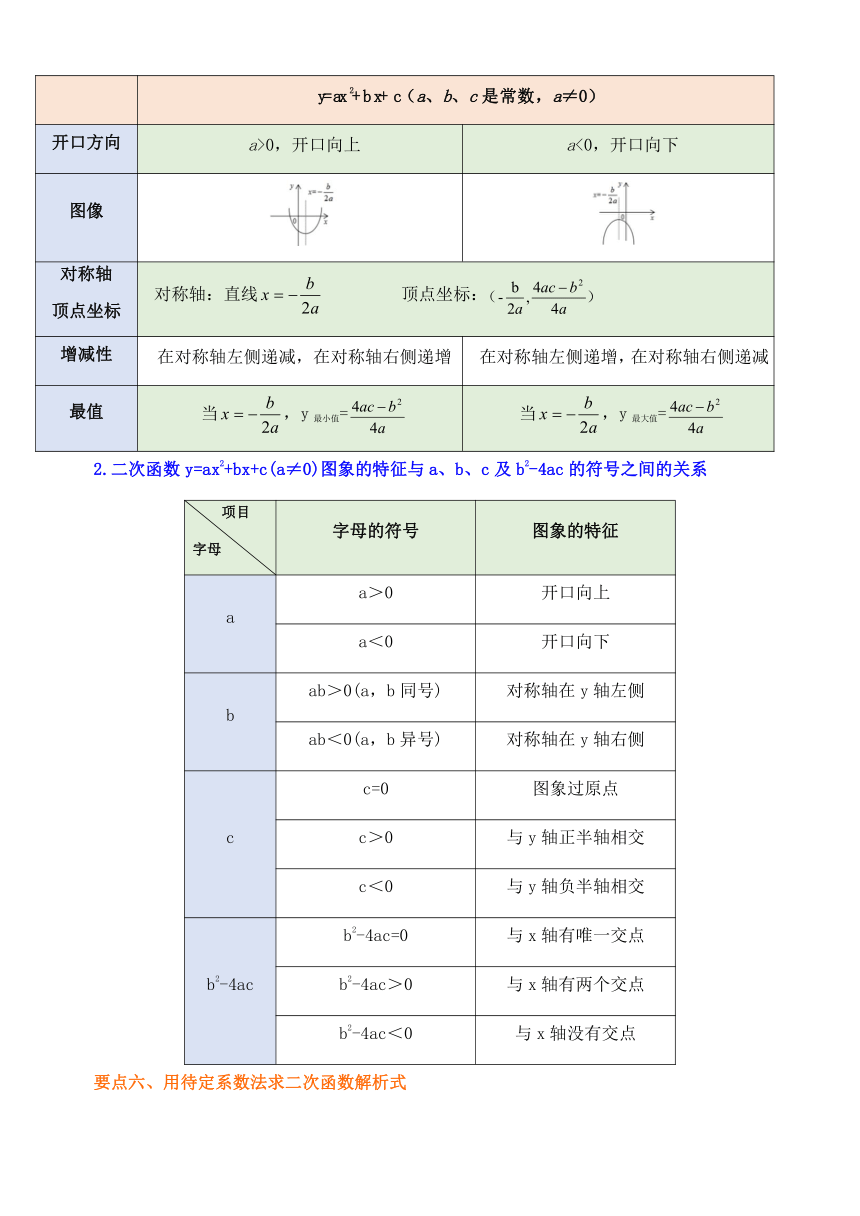
c(a、b、c是常数,a≠0)
开口方向
a>0,开口向上
a<0,开口向下
图像
对称轴
顶点坐标
对称轴:直线
顶点坐标:
增减性
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
最值
当,y最小值=
当,y最大值=
2.二次函数y=ax2+bx+c(a≠0)图象的特征与a、b、c及b2-4ac的符号之间的关系
项目
字母
字母的符号
图象的特征
a
a>0
开口向上
a<0
开口向下
b
ab>0(a,b同号)
对称轴在y轴左侧
ab<0(a,b异号)
对称轴在y轴右侧
c
c=0
图象过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
b2-4ac
b2-4ac=0
与x轴有唯一交点
b2-4ac>0
与x轴有两个交点
b2-4ac<0
与x轴没有交点
要点六、用待定系数法求二次函数解析式
1.二次函数解析式常见有以下几种形式
:
(1)一般式:
y=
ax
2
+
b
x+
c(a、b、c是常数,a≠0);
(2)顶点式:y=a(x-h)2+k(a,h,k为常数,a≠0);
(3)交点式:y=a(x-x1)(x-x2)(a≠0,x1
x2
是抛物线与x轴两交点的横坐标)
要点七、二次函数与一元二次方程的关系
1.二次函数图象与x轴的交点情况决定一元二次方程根的情况
判别式
△=b2-4ac
二次函数
y=
ax
2+bx+c(a、b、c是常数,a≠0)
一元二次方程
ax
2+bx+c=
0
图象
与x轴的交点坐标
根的情况
△>0
a>0
抛物线y=ax2+bx+c(a≠0)与x轴交于(x1,0)(x2,0)(x1一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根x1,2=
a<0
△=0
a>0
抛物线y=ax2+bx+c(a≠0)与x轴交切于()这一点,此时称抛物线与x轴相切
一元二次方程
ax2+bx+c=0(a≠0)有两个相等的实数根x1=x2
a<0
△<0
a>0
抛物线y=ax2+bx+c(a≠0)与x轴无交点,此时称抛物线与x轴相离
一元二次方程ax2+bx+c=0(a≠0)在实数范围内无解(或称无实数根)
a<0
要点八、抛物线与x轴的两个交点之间的距离公式
当△>0时,设抛物线y=ax2+bx+c与x轴的两个交点为A(x1,0),B(x2,0),则x1、x2
是一元二次方程ax2+bx+c=0的两个根.由根与系数的关系得x1+x2=-.x1x2=
即
要点九、抛物线与不等式的关系
二次函数y=
ax
2
+
b
x+
c(a≠0)与一元二次不等式ax2+bx+c>0(a≠0)及ax2+bx+c<0(a≠0)之间的关系如下(x1判别式
a>0
抛物线y=
ax
2
+
b
x+
c与
x轴的交点
不等式ax2+bx+c>0的解集
不等式ax2+bx+c<0的解集
△>0
△=0
无解
△<0
全体实数
无解
判别式
a<0
抛物线y=
ax
2
+
b
x+
c与
x轴的交点
不等式ax2+bx+c>0的解集
不等式ax2+bx+c<0的解集
△>0
△=0
△<0
要点十、列二次函数解应用题
二次函数,表示量与量的关系的代数式是含有两个变量的等式.
(1)审清题意,弄清题中涉及哪些量,已知量有几个,已知量与变量之间的基本关系是什么,找出等量关系(即函数关系).
(2)设出两个变量,注意分清自变量和因变量,同时还要注意所设变量的单位要准确.
(3)列函数表达式,抓住题中含有等量关系的语句,将此语句抽象为含变量的等式,这就是二次函数.
(4)按题目要求,结合二次函数的性质解答相应的问题。
(5)检验所得解是否符合实际:即是否为所提问题的答案.
(6)写出答案.
注:常见的问题:求最大(小)值(如求最大利润、最大面积、最小周长等)、涵洞、桥梁、抛物体、抛物线的模型问题等.解决这些实际问题关键是找等量关系,把实际问题转化为函数问题,列出相关的函数关系式.
要点十一、建立二次函数模型求解实际问题
一般步骤:(1)恰当地建立直角坐标系;(2)将已知条件转化为点的坐标;(3)合理地设出所求函数关系式;(4)代入已知条件或点的坐标,求出关系式;(5)利用关系式求解问题.
【重点难点】
类型一、二次函数的概念
Eg1.下列函数解析式中,一定为二次函数的是( ).
y=3x﹣1
B.
y=ax2+bx+c
C.
s=2t2﹣2t+1
D.
类型二、二次函数y=ax2(a≠0)的图象及性质
Eg2.函数y=x2的图象对称轴左侧上有两点A(a,15),B(b,),则a-b
0(>、<、=)
类型三、二次函数y=a(x-h)2+k(a≠0)图象、性质及综合应用
Eg3.1.二次函数y=﹣(x﹣3)2+2的顶点的坐标是
,对称轴是
.
Eg3.2.如图,抛物线顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)求△AOB的面积;
(3)若点P(m,-m)(m≠0)为抛物线上一点,求与P关于抛物线对称轴对称的点Q的坐标
类型四、二次函数
y=
a
x
2
+
b
x+
c(a≠0)的图象与性质、最值、综合应用
Eg4.1.求抛物线的对称轴和顶点坐标.
Eg4.2.求二次函数的最小值.
类型五、用待定系数法求二次函数解析式
Eg5.1已知二次函数的图象过(-1,-9)、(1,-3)和(3,-5)三点,求此二次函数的解析式.
Eg5.2已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.
类型六、用待定系数法解题
Eg6.已知抛物线经过(3,5),A(4,0),B(-2,0),且与y轴交于点C.
(1)求二次函数解析式;
(2)求△ABC的面积.
类型七、二次函数图象与坐标轴交点
Eg7.将抛物线y=x2﹣1向下平移8个单位长度后与x轴的两个交点之间的距离为( )
A.4
B.6
C.8
D.10
类型八、二次函数与一元二次方程的综合运用
Eg8.已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
类型九、二次函数与实际应用
1.利用二次函数求实际问题中的最大(小)值
Eg9.1某果园有100颗橙子树,平均每颗树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树.
(1)直接写出平均每棵树结的橙子个数y(个)与x之间的关系;
(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?
2.利用二次函数解决抛物线形建筑问题
Eg9.2如图所示,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形支撑架ADCB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
3.利用二次函数求图形面积问题
Eg9.4在一边靠墙的空地上,用砖墙围成三格矩形场地,如图所示.已知砖墙在地面上占地总长度160
m,问分隔墙在地面上的长度x为多少时所围场地总面积最大?并求最大面积?
4.利用二次函数求跳水、投篮等实际问题
Eg9.3某跳水运动员进行10
m跳台跳水训练时,身体(看作一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中最高处距水面m,入水处距池边的距离为4
m,同时,运动员在距离水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的关系式;
(2)在某次试跳中测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为m,问此次跳水会不会失误?并通过计算说明理由.
【考点过关】
1.对于抛物线y=-(x
+2)2﹣1,下列说法错误的是
A.开口向下
B.对称轴是直线x=﹣2
C.x>﹣2时,y随x的增大而增大
D.x=﹣2,函数有最大值y=﹣1
2.若关于的一元二次方程kx2-2x-1=0有两个不相等的实数根,则实数的取值范围是
A.k>-1
B.k<-1且k≠0
C.k>1且k≠0
D.k>-1且k≠0
3.已知点A(1,y1),B(2,y2)在抛物线上,则下列结论正确的是
A.2>y1>y2
B.2>y2>y1
C.y1>y2>2
D.y2>y1>2
4.如图抛物线与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)P为第二象限抛物线上的一个动点,求ACP面积的最大值.
5.如图,抛物线y1=x2﹣2与直线y2=x+4交于A,B两点.
(1)求A,B两点的坐标;
(2)当y1<y2时,直接写出自变量x的取值范围.
【课后作业】
1.二次函数y=–x2–2x+1配方后,结果正确的是
A.
B.
C.
D.
2.抛物线y=–(x–3)2+5,下列说法正确的是
A.开口向下,顶点坐标(3,5)
B.开口向上,顶点坐标(3,–5)
C.开口向下,顶点坐标(–3,5)
D.开口向上,顶点坐标(–3,–5)
3.将抛物线y=x
2–2x
+3向上平移1个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为
A.y=(x–1)2+3
B.y=(x–4)2+3
'
C.y=(x
+2)2+5
D.y=(x–4)2+5
4.已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.
知识脉络
①二次函数的图像和性质
②二次函数与一元二次方程
③实际问题与二次函数
【考点分析】
1.理解、掌握二次函数的概念和一般形式,根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围
2.确定函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标
3.二次函数y=ax2+bx+c的图象、顶点坐标与对称轴公式.
4.能运用二次函数及其图象确定方程和不等式的解或解集,根据函数图象与x轴的交点情况确定未知字母的值或取值范围.
5.运用二次函数求实际问题中的最大值或最小值.
6.应用二次函数的性质解决图形中最大面积问题.
7.利用二次函数解决拱桥及运动中的有关问题.
【基础知识】
要点一、二次函数的概念
1.二次函数的概念:一般地,形如y=ax2+bx+c(a≠0,a,
b,
c为常数)的函数是二次函数.
若b=0,则y=ax2+c;
若c=0,则y=ax2+bx;
若b=c=0,则y=ax2.
2.二次函数解析式的表示方法
1.
一般式:y=ax2+bx+c(a,b,c,为常数,a≠0)
2.
顶点式:y=a(x-h)2+k(a,h,k,为常数,a≠0)
3.
两根式:y=a(x-x1)(x-x2)(a≠0,x1
x2
是抛物线与x轴两交点的横坐标)或称交点式)
要点二、y=a(x-h)2+k(a,h,k,为常数,a≠0)函数的图象与性质
1.函数y=a(x-h)2+k的图象与性质
a的符号
开口方向
顶点坐标
对称轴
性质
a>0
向上
(h,k)
x=h
x>h时,y随x的增大而增大;x
向下
(h,k)
x=h
x>h时,y随x的增大而减小;x
二次函数y=a(x-h)2+k的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点三、二次函数的平移
1.平移步骤:
⑴
将抛物线解析式转化成顶点式y=a(x-h)2+k,确定其顶点坐标;
⑵
保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2.平移规律:在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.
要点四、二次函数y=ax2+bx+c(a,b,c,为常数,a≠0)的图象的画法
1.一般方法:列表、描点、连线;
①顶点坐标和对称轴,在直角坐标系中描出顶点,并用虚线画出对称轴.
②求抛物线y=ax2+bx+c与坐标轴的交点,再按顺序用平滑曲线连结起来.
要点五、二次函数y=ax2+bx+c(a≠0)的图象与性质
1.二次函数图象与性质
二次函数的定义
定义
一般地,形如
y=
ax
2
+
b
x+
c(a、b、c是常数,a≠0)的函数,叫做二次函数.
其中x、y是变量,a、b、c是常量
一般
形式
顶点式
y=a(x-h)2+k(a、h、k是常数,a≠0),其中(h,k)为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(h,k)
交点式
y=a(x-x1)(x-x2)(a是常数,a≠0),该形式的优势是能直接根据解析式得到抛物线与x轴的两个交点坐标(x1,0),(
x2,0)
y=
ax
2
(a≠0)
y=a(x-h)2+k(a≠0)
图像
开口方向
a>0时开口向上,a<0时开口向上
a>0时开口向上,a<0时开口向下
对称轴
直线x=0(y轴)
直线x=h
顶点坐标
(0,0)
(h,k)
增减性
a>0时,在对称轴左侧递减,在对称轴右侧递增
a<0时,在对称轴左侧递增,在对称轴右侧递减
最值
a>0,y最小值=0
/
a<0,y最小值=0(x=0)
a>0,y最小值=k
/
y最小值=k
(x=h)
y=
ax
2
+
b
x+
c(a、b、c是常数,a≠0)
开口方向
a>0,开口向上
a<0,开口向下
图像
对称轴
顶点坐标
对称轴:直线
顶点坐标:
增减性
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
最值
当,y最小值=
当,y最大值=
2.二次函数y=ax2+bx+c(a≠0)图象的特征与a、b、c及b2-4ac的符号之间的关系
项目
字母
字母的符号
图象的特征
a
a>0
开口向上
a<0
开口向下
b
ab>0(a,b同号)
对称轴在y轴左侧
ab<0(a,b异号)
对称轴在y轴右侧
c
c=0
图象过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
b2-4ac
b2-4ac=0
与x轴有唯一交点
b2-4ac>0
与x轴有两个交点
b2-4ac<0
与x轴没有交点
要点六、用待定系数法求二次函数解析式
1.二次函数解析式常见有以下几种形式
:
(1)一般式:
y=
ax
2
+
b
x+
c(a、b、c是常数,a≠0);
(2)顶点式:y=a(x-h)2+k(a,h,k为常数,a≠0);
(3)交点式:y=a(x-x1)(x-x2)(a≠0,x1
x2
是抛物线与x轴两交点的横坐标)
要点七、二次函数与一元二次方程的关系
1.二次函数图象与x轴的交点情况决定一元二次方程根的情况
判别式
△=b2-4ac
二次函数
y=
ax
2+bx+c(a、b、c是常数,a≠0)
一元二次方程
ax
2+bx+c=
0
图象
与x轴的交点坐标
根的情况
△>0
a>0
抛物线y=ax2+bx+c(a≠0)与x轴交于(x1,0)(x2,0)(x1
a<0
△=0
a>0
抛物线y=ax2+bx+c(a≠0)与x轴交切于()这一点,此时称抛物线与x轴相切
一元二次方程
ax2+bx+c=0(a≠0)有两个相等的实数根x1=x2
a<0
△<0
a>0
抛物线y=ax2+bx+c(a≠0)与x轴无交点,此时称抛物线与x轴相离
一元二次方程ax2+bx+c=0(a≠0)在实数范围内无解(或称无实数根)
a<0
要点八、抛物线与x轴的两个交点之间的距离公式
当△>0时,设抛物线y=ax2+bx+c与x轴的两个交点为A(x1,0),B(x2,0),则x1、x2
是一元二次方程ax2+bx+c=0的两个根.由根与系数的关系得x1+x2=-.x1x2=
即
要点九、抛物线与不等式的关系
二次函数y=
ax
2
+
b
x+
c(a≠0)与一元二次不等式ax2+bx+c>0(a≠0)及ax2+bx+c<0(a≠0)之间的关系如下(x1
a>0
抛物线y=
ax
2
+
b
x+
c与
x轴的交点
不等式ax2+bx+c>0的解集
不等式ax2+bx+c<0的解集
△>0
△=0
无解
△<0
全体实数
无解
判别式
a<0
抛物线y=
ax
2
+
b
x+
c与
x轴的交点
不等式ax2+bx+c>0的解集
不等式ax2+bx+c<0的解集
△>0
△=0
△<0
要点十、列二次函数解应用题
二次函数,表示量与量的关系的代数式是含有两个变量的等式.
(1)审清题意,弄清题中涉及哪些量,已知量有几个,已知量与变量之间的基本关系是什么,找出等量关系(即函数关系).
(2)设出两个变量,注意分清自变量和因变量,同时还要注意所设变量的单位要准确.
(3)列函数表达式,抓住题中含有等量关系的语句,将此语句抽象为含变量的等式,这就是二次函数.
(4)按题目要求,结合二次函数的性质解答相应的问题。
(5)检验所得解是否符合实际:即是否为所提问题的答案.
(6)写出答案.
注:常见的问题:求最大(小)值(如求最大利润、最大面积、最小周长等)、涵洞、桥梁、抛物体、抛物线的模型问题等.解决这些实际问题关键是找等量关系,把实际问题转化为函数问题,列出相关的函数关系式.
要点十一、建立二次函数模型求解实际问题
一般步骤:(1)恰当地建立直角坐标系;(2)将已知条件转化为点的坐标;(3)合理地设出所求函数关系式;(4)代入已知条件或点的坐标,求出关系式;(5)利用关系式求解问题.
【重点难点】
类型一、二次函数的概念
Eg1.下列函数解析式中,一定为二次函数的是( ).
y=3x﹣1
B.
y=ax2+bx+c
C.
s=2t2﹣2t+1
D.
类型二、二次函数y=ax2(a≠0)的图象及性质
Eg2.函数y=x2的图象对称轴左侧上有两点A(a,15),B(b,),则a-b
0(>、<、=)
类型三、二次函数y=a(x-h)2+k(a≠0)图象、性质及综合应用
Eg3.1.二次函数y=﹣(x﹣3)2+2的顶点的坐标是
,对称轴是
.
Eg3.2.如图,抛物线顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)求△AOB的面积;
(3)若点P(m,-m)(m≠0)为抛物线上一点,求与P关于抛物线对称轴对称的点Q的坐标
类型四、二次函数
y=
a
x
2
+
b
x+
c(a≠0)的图象与性质、最值、综合应用
Eg4.1.求抛物线的对称轴和顶点坐标.
Eg4.2.求二次函数的最小值.
类型五、用待定系数法求二次函数解析式
Eg5.1已知二次函数的图象过(-1,-9)、(1,-3)和(3,-5)三点,求此二次函数的解析式.
Eg5.2已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.
类型六、用待定系数法解题
Eg6.已知抛物线经过(3,5),A(4,0),B(-2,0),且与y轴交于点C.
(1)求二次函数解析式;
(2)求△ABC的面积.
类型七、二次函数图象与坐标轴交点
Eg7.将抛物线y=x2﹣1向下平移8个单位长度后与x轴的两个交点之间的距离为( )
A.4
B.6
C.8
D.10
类型八、二次函数与一元二次方程的综合运用
Eg8.已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
类型九、二次函数与实际应用
1.利用二次函数求实际问题中的最大(小)值
Eg9.1某果园有100颗橙子树,平均每颗树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树.
(1)直接写出平均每棵树结的橙子个数y(个)与x之间的关系;
(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?
2.利用二次函数解决抛物线形建筑问题
Eg9.2如图所示,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形支撑架ADCB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
3.利用二次函数求图形面积问题
Eg9.4在一边靠墙的空地上,用砖墙围成三格矩形场地,如图所示.已知砖墙在地面上占地总长度160
m,问分隔墙在地面上的长度x为多少时所围场地总面积最大?并求最大面积?
4.利用二次函数求跳水、投篮等实际问题
Eg9.3某跳水运动员进行10
m跳台跳水训练时,身体(看作一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中最高处距水面m,入水处距池边的距离为4
m,同时,运动员在距离水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的关系式;
(2)在某次试跳中测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为m,问此次跳水会不会失误?并通过计算说明理由.
【考点过关】
1.对于抛物线y=-(x
+2)2﹣1,下列说法错误的是
A.开口向下
B.对称轴是直线x=﹣2
C.x>﹣2时,y随x的增大而增大
D.x=﹣2,函数有最大值y=﹣1
2.若关于的一元二次方程kx2-2x-1=0有两个不相等的实数根,则实数的取值范围是
A.k>-1
B.k<-1且k≠0
C.k>1且k≠0
D.k>-1且k≠0
3.已知点A(1,y1),B(2,y2)在抛物线上,则下列结论正确的是
A.2>y1>y2
B.2>y2>y1
C.y1>y2>2
D.y2>y1>2
4.如图抛物线与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)P为第二象限抛物线上的一个动点,求ACP面积的最大值.
5.如图,抛物线y1=x2﹣2与直线y2=x+4交于A,B两点.
(1)求A,B两点的坐标;
(2)当y1<y2时,直接写出自变量x的取值范围.
【课后作业】
1.二次函数y=–x2–2x+1配方后,结果正确的是
A.
B.
C.
D.
2.抛物线y=–(x–3)2+5,下列说法正确的是
A.开口向下,顶点坐标(3,5)
B.开口向上,顶点坐标(3,–5)
C.开口向下,顶点坐标(–3,5)
D.开口向上,顶点坐标(–3,–5)
3.将抛物线y=x
2–2x
+3向上平移1个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为
A.y=(x–1)2+3
B.y=(x–4)2+3
'
C.y=(x
+2)2+5
D.y=(x–4)2+5
4.已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.
知识脉络
同课章节目录
