人教版九年级数学上册课件:24.4.1 弧长和扇形面积(共18张)
文档属性
| 名称 | 人教版九年级数学上册课件:24.4.1 弧长和扇形面积(共18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 386.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 22:01:40 | ||
图片预览




文档简介
(共18张PPT)
24.4.1
弧长和扇形面积
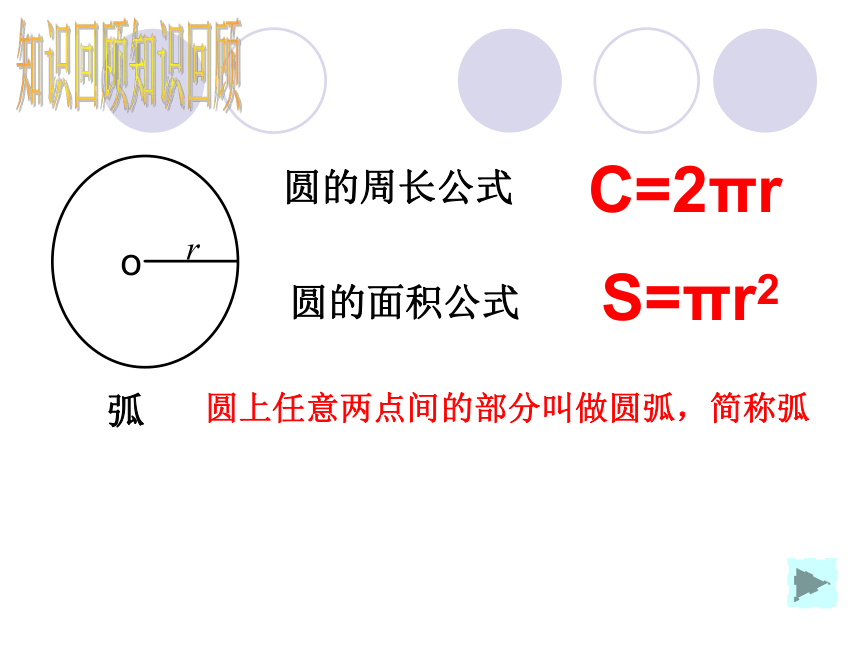
o
圆的周长公式
圆的面积公式
C=2πr
S=πr2
弧
圆上任意两点间的部分叫做圆弧,简称弧
知识回顾
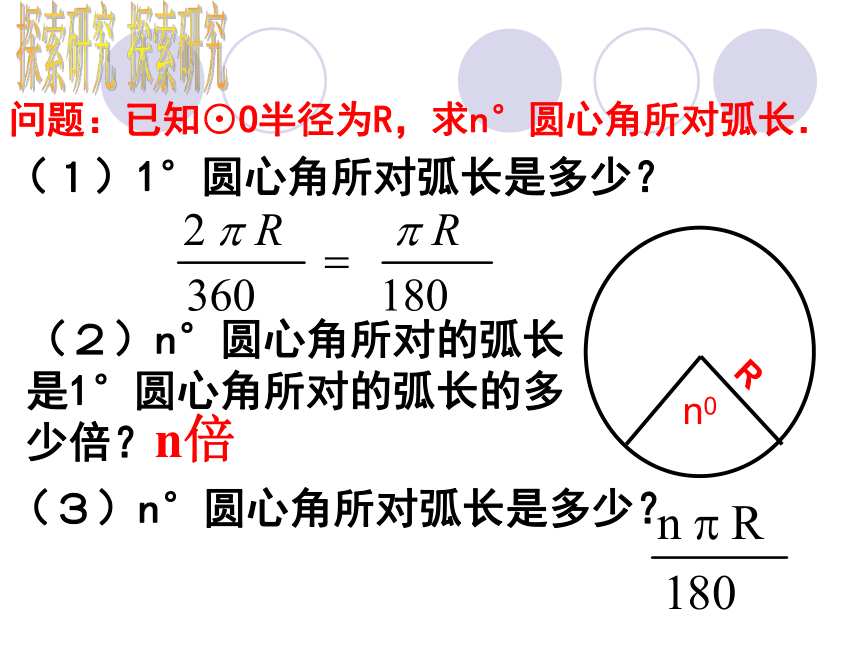
问题:已知⊙O半径为R,求n°圆心角所对弧长.
(1)1°圆心角所对弧长是多少?
(2)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
n倍
(3)n°圆心角所对弧长是多少?
n0
R
探索研究
若设⊙O半径为R,
n°的圆心角所对的弧长为L,则
(1)在应用弧长公式L
,
进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
注意:
弧长公式
在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有多大?
(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?
问题探究
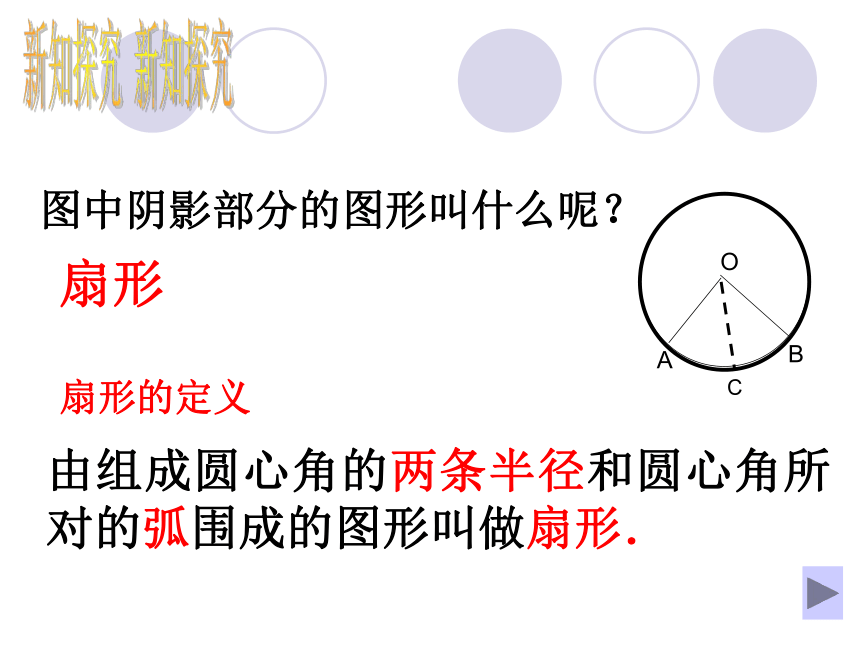
扇形的定义
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
A
B
O
图中阴影部分的图形叫什么呢?
扇形
新知探究
C
已知⊙O半径为R,求圆心角n°的扇形的面积?
(1)圆面积可以看作是多少度的圆心角所对的扇形的面积?
360°
(2)圆心角为1°的扇形的面积是多少?
(3)圆心角为n°的扇形的面积是圆心角为
1°的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少?
探索研究
若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形=
注意:
在应用扇形的面积公式S扇形=
进行计算时,要注意公式中n的意义.
n表示1°圆心角的倍数,它是不带单位的
扇形面积
比较弧长公式与扇形面积公式
l
弧
=
πR
180
n
S扇形
360
n
=
πR2
在这两个公式中,弧长和扇形面积都和圆心角n°、半径R有关系,因此l
和S之间也有一定的关系,你能猜得出吗?
生活中的数学、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,
可得弧AB
的长
l
(mm)
因此所要求的展直长度
L
(mm)
答:管道的展直长度为2970mm.
例题讲解
例:如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m2)。
0
B
A
C
D
例题讲解
2、已知半径为2的扇形,面积为
,
则它的圆心角的度数为___.
3、已知半径为2的扇形,面积为
,
则这个扇形的弧长=____.
10∏
120°
小试牛刀
1、已知圆弧的半径为30厘米,圆心
角为60°,则此圆弧的长度为___
4.如图所示,把边长为2的正方形ABCD的一边放在定直线L上,按顺时针方向绕点D旋转到如图的位置,则点B运动到点B′所经过的路线长度为
________
A
C
B
D
B/
C/
(A/)
L
一、弧长的计算公式
二、扇形面积计算公式
课堂小结
这节课你有什么收获?
1.如图,A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于
。
拓展提高
2.如图,已知P、Q分别是半径为1的半圆圆周上的两个三等分点,AB是直径,则阴影部分的面积等于
。
拓展提高
3.已知如图所示,扇形所在圆的半径为R,AB的长为R,⊙O′和OA、OB分别相切于点C、E,且与⊙O内切于点D,求⊙O′的周长.
拓展提高
作业
课本
P122页
1、2
24.4.1
弧长和扇形面积
o
圆的周长公式
圆的面积公式
C=2πr
S=πr2
弧
圆上任意两点间的部分叫做圆弧,简称弧
知识回顾
问题:已知⊙O半径为R,求n°圆心角所对弧长.
(1)1°圆心角所对弧长是多少?
(2)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
n倍
(3)n°圆心角所对弧长是多少?
n0
R
探索研究
若设⊙O半径为R,
n°的圆心角所对的弧长为L,则
(1)在应用弧长公式L
,
进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
注意:
弧长公式
在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有多大?
(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?
问题探究
扇形的定义
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
A
B
O
图中阴影部分的图形叫什么呢?
扇形
新知探究
C
已知⊙O半径为R,求圆心角n°的扇形的面积?
(1)圆面积可以看作是多少度的圆心角所对的扇形的面积?
360°
(2)圆心角为1°的扇形的面积是多少?
(3)圆心角为n°的扇形的面积是圆心角为
1°的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少?
探索研究
若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形=
注意:
在应用扇形的面积公式S扇形=
进行计算时,要注意公式中n的意义.
n表示1°圆心角的倍数,它是不带单位的
扇形面积
比较弧长公式与扇形面积公式
l
弧
=
πR
180
n
S扇形
360
n
=
πR2
在这两个公式中,弧长和扇形面积都和圆心角n°、半径R有关系,因此l
和S之间也有一定的关系,你能猜得出吗?
生活中的数学、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,
可得弧AB
的长
l
(mm)
因此所要求的展直长度
L
(mm)
答:管道的展直长度为2970mm.
例题讲解
例:如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m2)。
0
B
A
C
D
例题讲解
2、已知半径为2的扇形,面积为
,
则它的圆心角的度数为___.
3、已知半径为2的扇形,面积为
,
则这个扇形的弧长=____.
10∏
120°
小试牛刀
1、已知圆弧的半径为30厘米,圆心
角为60°,则此圆弧的长度为___
4.如图所示,把边长为2的正方形ABCD的一边放在定直线L上,按顺时针方向绕点D旋转到如图的位置,则点B运动到点B′所经过的路线长度为
________
A
C
B
D
B/
C/
(A/)
L
一、弧长的计算公式
二、扇形面积计算公式
课堂小结
这节课你有什么收获?
1.如图,A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于
。
拓展提高
2.如图,已知P、Q分别是半径为1的半圆圆周上的两个三等分点,AB是直径,则阴影部分的面积等于
。
拓展提高
3.已知如图所示,扇形所在圆的半径为R,AB的长为R,⊙O′和OA、OB分别相切于点C、E,且与⊙O内切于点D,求⊙O′的周长.
拓展提高
作业
课本
P122页
1、2
同课章节目录
