人教版九年级数学上册22.1.1二次函数(1)课件(共23张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.1.1二次函数(1)课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第二十二章
二次函数
22.1.1二次函数
学习目标
1.理解掌握二次函数的概念和一般形式.(重点)
2.会利用二次函数的概念解决问题.
3.会列二次函数表达式解决实际问题.(难点)
雨后天空的彩虹,公园里的喷泉,跳绳等都会形成一条曲线.这些曲线能否用函数关系式表示?
导入新课
情境引入
1.
函数的定义:
(在某个变化过程中,有两个变量x和y,对于x在某一范围内的每一个确定的值,变量y都有一个唯一确定的值与它对应,那么我们称y是x的函数,其中x是自变量,y是x的函数.)
2.
大家还记得我们学过哪些函数吗?
(
正比例函数,一次函数)
问题1:
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
y=6x2①
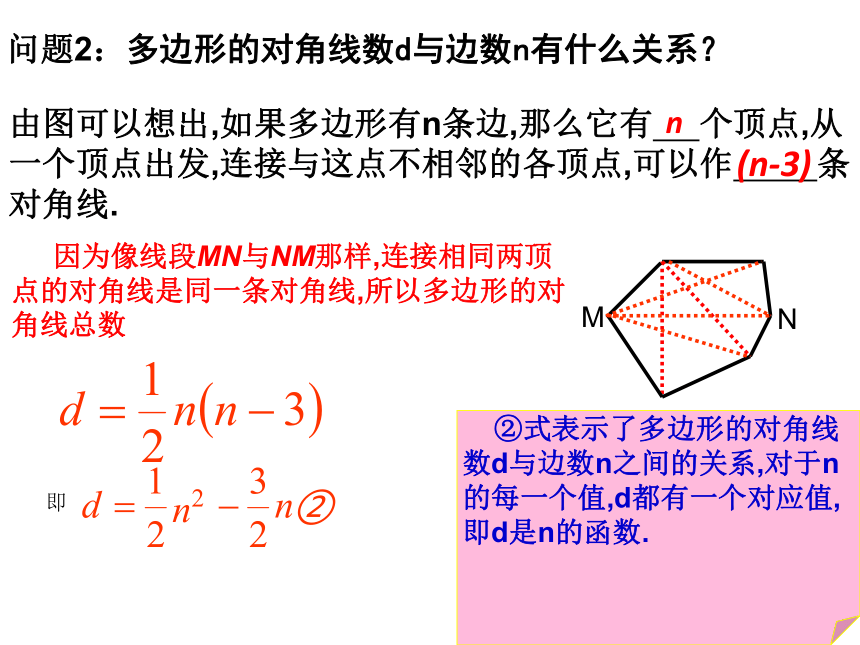
问题2:多边形的对角线数d与边数n有什么关系?
由图可以想出,如果多边形有n条边,那么它有
个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作
条对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
M
N
即
②式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有一个对应值,即d是n的函数.
问题3:
某工厂一种产品今年的年产量是20件,计划明后两年增加产量.如果每年的增长率为x,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
分析:这种产品的原产量是20件,
一年后的产量是
件,再经过一年后的产量是
件,即两年后的产量为
20(1+x)
20(1+x)2
即
③式表示了两年后的产量y与增长率x之间的关系,对于x的每一个值,
y都有一个对应值,即y是x的函数.
y是x的函数吗?
y是x的一次函数?
2定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠
0)的函数叫做二次函数。
观察与总结
y=6x2①
我们把形如y=ax?+bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数
知识归纳
为什么a
≠0呢?
称:a为二次项系数,
ax2叫做二次项
b为一次项系数,
bx叫做一次项
c为常数项,
二次函数的一般形式:
yy=ax2+bx+c
(其中a、b、c是常,a≠0)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
观察与总结
二次函数的一般形式:
函数解析式
二次项系数a
一次项系数b
常数项
c
0
0
2
4
2
-1
58
-112
13
0
说出下列二次函数的二次项系数、一次项系数和常数项:
二次函数y=ax?+bx+c中a≠0,而b、c可以为0.
例题与练习
例.
y=(m+3)x
(1)
m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是二次函数?
m2-7
小结:
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)y=ax?+c(a≠0,b=0,c≠0).
(3)y=ax?+bx(a≠0,b≠0,c=0).
2.定义的实质是:ax?+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
A
组
1.
下列二次函数的二次项系数是-3的是
(
)
A.
y=3x2-2x+5
B.
y=x2-3x+2
C.
y=-3x2-x
D.
y=x2-3
C
当堂检测
2.
下列函数中,y是x的二次函数的是
(
)
A.
y=
B.
y=5x+3
C.
y=x2-3
D.
y=
C
3.
下列函数是二次函数的是
(
)
A.
在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.
当距离一定时,火车行驶的时间t与速度v之间的关系
C.
等边三角形的周长C与边长a之间的关系
D.
圆的面积S与半径R之间的关系
D
4.
若函数y=(a-3)x2+x+a是二次函数,那么a不可以取
(
)
A.
0
B.
1
C.
2
D.
3
D
5.
若函数y=(m-3)xm-2是二次函数,则m的值为____________.
6.
二次函数y=3x2+5的二次项系数是____________,一次项系数是____________.
4
3
0
B
组
7.
下列函数不是二次函数的是
(
)
A.
y=(x-1)2
B.
y=1-
C.
y=-(x+1)(x-1)
D.
y=2(x+3)2-2x2
D
8.
已知函数y=(m2-m)x2+mx+(m+1),m是常数.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,求m的值.
解:(1)依题意,m2-m=0且m≠0.
解得m=1.
(2)依题意,m2-m≠0.
解得m≠1且m≠0.
9.
一个二次函数y=(k-1)xk2-3k+4+2x-1.
(1)求k的值;
(2)求当x=0.5时,y的值.
解:(1)由题意,得
解得k=2.
(2)把k=2代入y=(k-1)xk2-3k+4+2x-1,
得y=x2+2x-1.
当x=0.5时,y=0.52+2×0.5-1=0.25.
C
组
10.
已知y=(m+2)xm2-2是二次函数,则m=____________.
2
第二十二章
二次函数
22.1.1二次函数
学习目标
1.理解掌握二次函数的概念和一般形式.(重点)
2.会利用二次函数的概念解决问题.
3.会列二次函数表达式解决实际问题.(难点)
雨后天空的彩虹,公园里的喷泉,跳绳等都会形成一条曲线.这些曲线能否用函数关系式表示?
导入新课
情境引入
1.
函数的定义:
(在某个变化过程中,有两个变量x和y,对于x在某一范围内的每一个确定的值,变量y都有一个唯一确定的值与它对应,那么我们称y是x的函数,其中x是自变量,y是x的函数.)
2.
大家还记得我们学过哪些函数吗?
(
正比例函数,一次函数)
问题1:
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
y=6x2①
问题2:多边形的对角线数d与边数n有什么关系?
由图可以想出,如果多边形有n条边,那么它有
个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作
条对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
M
N
即
②式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有一个对应值,即d是n的函数.
问题3:
某工厂一种产品今年的年产量是20件,计划明后两年增加产量.如果每年的增长率为x,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
分析:这种产品的原产量是20件,
一年后的产量是
件,再经过一年后的产量是
件,即两年后的产量为
20(1+x)
20(1+x)2
即
③式表示了两年后的产量y与增长率x之间的关系,对于x的每一个值,
y都有一个对应值,即y是x的函数.
y是x的函数吗?
y是x的一次函数?
2定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠
0)的函数叫做二次函数。
观察与总结
y=6x2①
我们把形如y=ax?+bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数
知识归纳
为什么a
≠0呢?
称:a为二次项系数,
ax2叫做二次项
b为一次项系数,
bx叫做一次项
c为常数项,
二次函数的一般形式:
yy=ax2+bx+c
(其中a、b、c是常,a≠0)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
观察与总结
二次函数的一般形式:
函数解析式
二次项系数a
一次项系数b
常数项
c
0
0
2
4
2
-1
58
-112
13
0
说出下列二次函数的二次项系数、一次项系数和常数项:
二次函数y=ax?+bx+c中a≠0,而b、c可以为0.
例题与练习
例.
y=(m+3)x
(1)
m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是二次函数?
m2-7
小结:
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)y=ax?+c(a≠0,b=0,c≠0).
(3)y=ax?+bx(a≠0,b≠0,c=0).
2.定义的实质是:ax?+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
A
组
1.
下列二次函数的二次项系数是-3的是
(
)
A.
y=3x2-2x+5
B.
y=x2-3x+2
C.
y=-3x2-x
D.
y=x2-3
C
当堂检测
2.
下列函数中,y是x的二次函数的是
(
)
A.
y=
B.
y=5x+3
C.
y=x2-3
D.
y=
C
3.
下列函数是二次函数的是
(
)
A.
在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.
当距离一定时,火车行驶的时间t与速度v之间的关系
C.
等边三角形的周长C与边长a之间的关系
D.
圆的面积S与半径R之间的关系
D
4.
若函数y=(a-3)x2+x+a是二次函数,那么a不可以取
(
)
A.
0
B.
1
C.
2
D.
3
D
5.
若函数y=(m-3)xm-2是二次函数,则m的值为____________.
6.
二次函数y=3x2+5的二次项系数是____________,一次项系数是____________.
4
3
0
B
组
7.
下列函数不是二次函数的是
(
)
A.
y=(x-1)2
B.
y=1-
C.
y=-(x+1)(x-1)
D.
y=2(x+3)2-2x2
D
8.
已知函数y=(m2-m)x2+mx+(m+1),m是常数.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,求m的值.
解:(1)依题意,m2-m=0且m≠0.
解得m=1.
(2)依题意,m2-m≠0.
解得m≠1且m≠0.
9.
一个二次函数y=(k-1)xk2-3k+4+2x-1.
(1)求k的值;
(2)求当x=0.5时,y的值.
解:(1)由题意,得
解得k=2.
(2)把k=2代入y=(k-1)xk2-3k+4+2x-1,
得y=x2+2x-1.
当x=0.5时,y=0.52+2×0.5-1=0.25.
C
组
10.
已知y=(m+2)xm2-2是二次函数,则m=____________.
2
同课章节目录
