华师大版七年级数学上册2.13有理数的混合运算课件(共20张PPT)
文档属性
| 名称 | 华师大版七年级数学上册2.13有理数的混合运算课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 493.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 19:00:41 | ||
图片预览







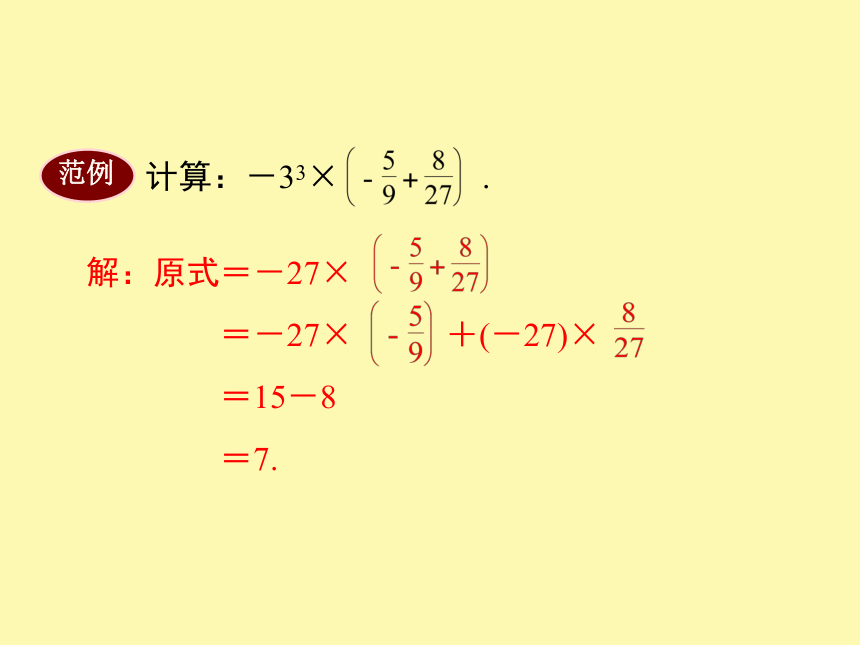
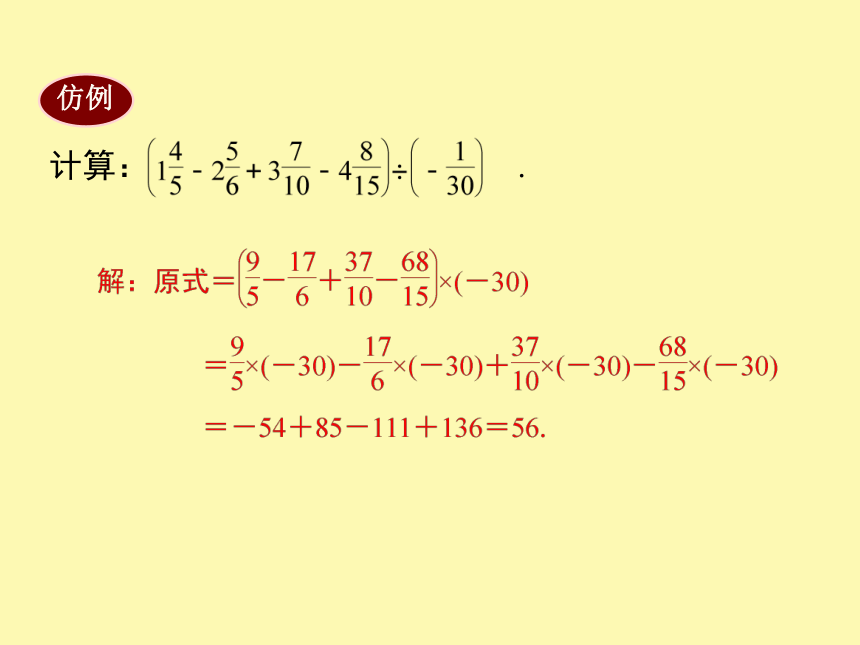
文档简介
(共20张PPT)
第2章
有理数
2.13
有理数的混合运算
华师版数学七年级上册
【学习目标】
1.让学生了解有理数混合运算的意义,掌握有理数的混合运算法则及运算顺序;
2.让学生能够熟练地进行有理数的加、减、乘、除、乘方的运算,并在运算过程中合理使用运算律;
3.培养学生对数的感觉,提高学生正确运算的能力,培养学生思维的逻辑性和灵活性,进一步发展学生的思维能力.
【学习重点】
有理数的混合运算顺序、运算法则和运算律的应用.
【学习难点】
有理数的混合运算.
学习目标
1.指出下列各幂是正数还是负数.
38,(-1)3,(-2)4、
、(-7)8、(-8)7.
答:正、负、正、正、正、负.
2.我们学过了有理数的哪些运算律?
答:加法交换律、结合律;乘法交换律、结合律、分配律.
我们已学过了加减乘除四则运算,知道了它们的运算顺序.现在又多了一种乘方运算,我们应该如何进行呢?这就是我们这一节课要研究的内容.
导入新知
知识模块一
有理数的混合运算
阅读教材P61~P64,完成下面的内容.
下面的算式中有哪几种运算?
(1)2+32×(-6); (2)3+50÷22×
-1.
归纳:(1)这两个算式中,含有有理数的加、减、乘、除、乘方等多种运算,它是有理数的混合运算.
(2)有理数的混合运算顺序是:①先算乘方,再算乘除,最后算加减;
②同级运算,按照从左至右的顺序进行;
③如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
探究新知
范例
计算:
(2)
+(-2)5×0;
(2)原式=π-3.14+0=π-3.14;
解:
知识模块二 有理数混合运算中的简便运算
归纳:进行有理数混合运算时,运用运算律可使运算简便.乘法对加法的分配律的运用有以下两种形式:①把乘积形式化成和的形式,如(a+b)c=ac+bc;②把和的形式化成积的形式,如:ac+bc=(a+b)c.
范例
计算:-33×
.
解:原式=-27×
=-27×
+(-27)×
=15-8
=7.
仿例
计算:
.
变例
计算:
.
课堂练习
1.在(-1)3,(-1)2,-22,(-3)2这四个数中,最大的数与最小的数的和等于( )
A.6
B.8
C.-5
D.5
D
2.定义一种新运算:a?b=b2-ab,如:1?2=22-1×2=2,则(-1?2)?3=______.
-7
3.计算:
(1)(-1)10×2+(-2)3÷4;
(2)(-5)3-3×(-
)4;
(3)-14-2×(-3)2÷(-
);
(4)
÷
-
×(-6)2+32.
(1)0
(2)-125
(3)107
(4)-
解:
4.数学课上老师出了一道题,计算:1+21+22+23+24+25+26+27+28+29,老师在教室里巡视了一圈,发现同学们都做不出来,于是给出解答:
解:令s=1+21+22+23+24+25+26+27+28+29,①
则2s=2+22+23+24+25+26+27+28+29+210,②
②-①,得s=210-1.
根据以上方法计算:
1+2+22+23+…+22
015(写出过程,结果用幂表示).
解:22
016-1
5.某文具店在一周的销售中,盈亏情况如下表(盈余为正,单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
-27.8
-70.3
200
138.1
-8
?
188
458
表中星期六的盈亏数被墨水涂污了,请你算出星期六的盈亏数,并说明星期六是盈还是亏?盈亏是多少?
解:星期六盈利,盈利38元.
6.某市旅游局发布统计报告,国庆期间,溱湖风景区在7天假期中每天接待游客的人数变化如下表所示(正数表示比前一天多的人数,负数表示比前一天少的人数):
(1)若9月30日的游客人数记为m万人,请用式子表示10月3日的游客人数.
(2)若9月30日的游客人数为0.6万人,门票每人100元,则国庆期间溱湖风景区的门票收入是多少元?(用科学记数法表示)
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化
/万人
+1.2
+0.8
+0.2
-0.2
-0.6
+0.2
-1
解:
(1)(m+2.2)万人
(2)1.52×107元
再
见
第2章
有理数
2.13
有理数的混合运算
华师版数学七年级上册
【学习目标】
1.让学生了解有理数混合运算的意义,掌握有理数的混合运算法则及运算顺序;
2.让学生能够熟练地进行有理数的加、减、乘、除、乘方的运算,并在运算过程中合理使用运算律;
3.培养学生对数的感觉,提高学生正确运算的能力,培养学生思维的逻辑性和灵活性,进一步发展学生的思维能力.
【学习重点】
有理数的混合运算顺序、运算法则和运算律的应用.
【学习难点】
有理数的混合运算.
学习目标
1.指出下列各幂是正数还是负数.
38,(-1)3,(-2)4、
、(-7)8、(-8)7.
答:正、负、正、正、正、负.
2.我们学过了有理数的哪些运算律?
答:加法交换律、结合律;乘法交换律、结合律、分配律.
我们已学过了加减乘除四则运算,知道了它们的运算顺序.现在又多了一种乘方运算,我们应该如何进行呢?这就是我们这一节课要研究的内容.
导入新知
知识模块一
有理数的混合运算
阅读教材P61~P64,完成下面的内容.
下面的算式中有哪几种运算?
(1)2+32×(-6); (2)3+50÷22×
-1.
归纳:(1)这两个算式中,含有有理数的加、减、乘、除、乘方等多种运算,它是有理数的混合运算.
(2)有理数的混合运算顺序是:①先算乘方,再算乘除,最后算加减;
②同级运算,按照从左至右的顺序进行;
③如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
探究新知
范例
计算:
(2)
+(-2)5×0;
(2)原式=π-3.14+0=π-3.14;
解:
知识模块二 有理数混合运算中的简便运算
归纳:进行有理数混合运算时,运用运算律可使运算简便.乘法对加法的分配律的运用有以下两种形式:①把乘积形式化成和的形式,如(a+b)c=ac+bc;②把和的形式化成积的形式,如:ac+bc=(a+b)c.
范例
计算:-33×
.
解:原式=-27×
=-27×
+(-27)×
=15-8
=7.
仿例
计算:
.
变例
计算:
.
课堂练习
1.在(-1)3,(-1)2,-22,(-3)2这四个数中,最大的数与最小的数的和等于( )
A.6
B.8
C.-5
D.5
D
2.定义一种新运算:a?b=b2-ab,如:1?2=22-1×2=2,则(-1?2)?3=______.
-7
3.计算:
(1)(-1)10×2+(-2)3÷4;
(2)(-5)3-3×(-
)4;
(3)-14-2×(-3)2÷(-
);
(4)
÷
-
×(-6)2+32.
(1)0
(2)-125
(3)107
(4)-
解:
4.数学课上老师出了一道题,计算:1+21+22+23+24+25+26+27+28+29,老师在教室里巡视了一圈,发现同学们都做不出来,于是给出解答:
解:令s=1+21+22+23+24+25+26+27+28+29,①
则2s=2+22+23+24+25+26+27+28+29+210,②
②-①,得s=210-1.
根据以上方法计算:
1+2+22+23+…+22
015(写出过程,结果用幂表示).
解:22
016-1
5.某文具店在一周的销售中,盈亏情况如下表(盈余为正,单位:元):
星期一
星期二
星期三
星期四
星期五
星期六
星期日
合计
-27.8
-70.3
200
138.1
-8
?
188
458
表中星期六的盈亏数被墨水涂污了,请你算出星期六的盈亏数,并说明星期六是盈还是亏?盈亏是多少?
解:星期六盈利,盈利38元.
6.某市旅游局发布统计报告,国庆期间,溱湖风景区在7天假期中每天接待游客的人数变化如下表所示(正数表示比前一天多的人数,负数表示比前一天少的人数):
(1)若9月30日的游客人数记为m万人,请用式子表示10月3日的游客人数.
(2)若9月30日的游客人数为0.6万人,门票每人100元,则国庆期间溱湖风景区的门票收入是多少元?(用科学记数法表示)
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化
/万人
+1.2
+0.8
+0.2
-0.2
-0.6
+0.2
-1
解:
(1)(m+2.2)万人
(2)1.52×107元
再
见
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
