沪科版八年级上册12.2一次函数同步测试(word版含答案)
文档属性
| 名称 | 沪科版八年级上册12.2一次函数同步测试(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 272.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 08:47:38 | ||
图片预览



文档简介
12.2一次函数单元测试
(时间90分钟
满分120分
)
一、选择题(计40每题4分)
1.有下列函数:(1)y=kx;(2)y=2x-1;(3)y=;(4)y=2-1-3x;(5)y=x2-1.其中是一次函数的有
( )
A.1个
B.2个
C.3个
D.4个
2.如图,直线y=2x必过的点是( )
A.(2,1)
B.(2,2)
C.(-1,-1)
D.(0,0)
如图
3.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
4.将直线y=2x向上平移1个单位,得到的直线的函数表达式为
( )
A.y=2x+1
B.y=2x-1
C.y=2(x+1)
D.y=2(x-1)
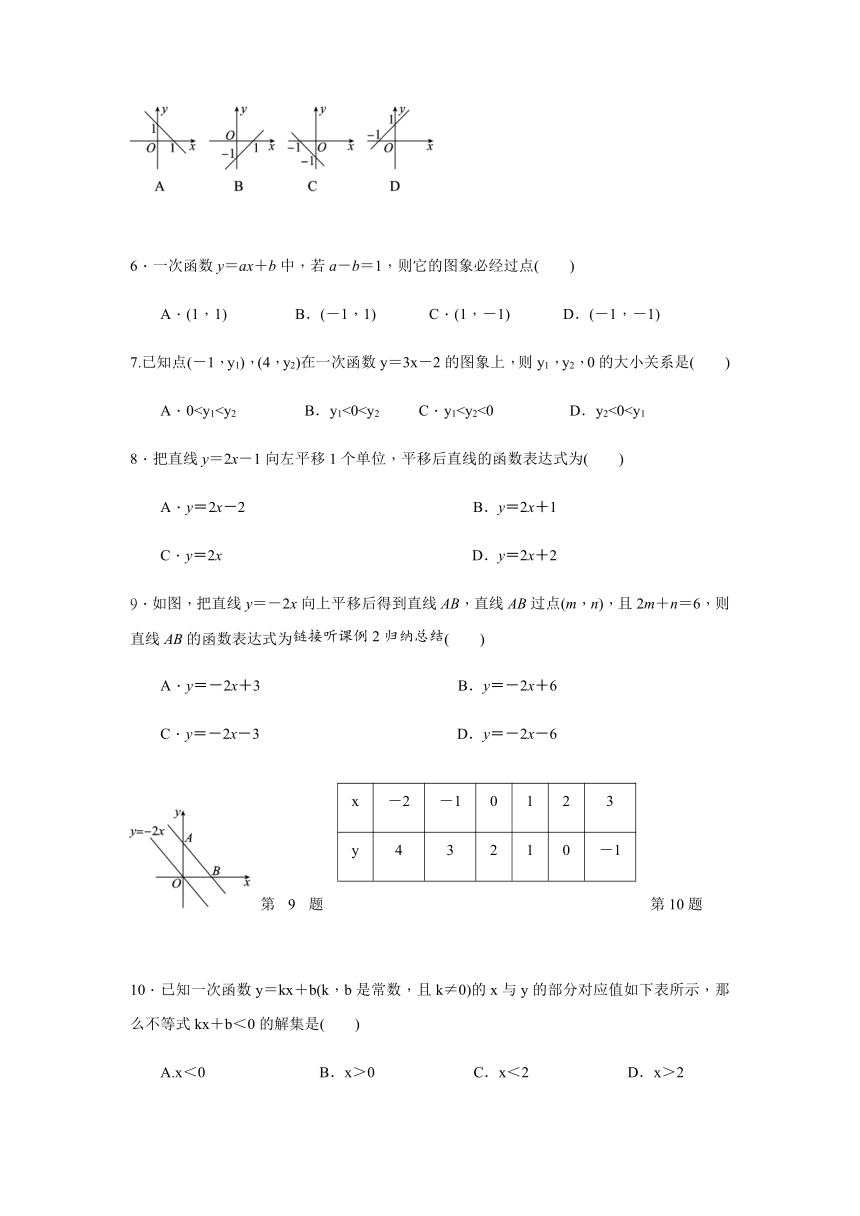
5.在平面直角坐标系中,一次函数y=x-1的图象是
( )
6.一次函数y=ax+b中,若a-b=1,则它的图象必经过点( )
A.(1,1)
B.(-1,1)
C.(1,-1)
D.(-1,-1)
7.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
A.0B.y1<0C.y1D.y2<08.把直线y=2x-1向左平移1个单位,平移后直线的函数表达式为( )
A.y=2x-2
B.y=2x+1
C.y=2x
D.y=2x+2
9.如图,把直线y=-2x向上平移后得到直线AB,直线AB过点(m,n),且2m+n=6,则直线AB的函数表达式为( )
A.y=-2x+3
B.y=-2x+6
C.y=-2x-3
D.y=-2x-6
x
-2
-1
0
1
2
3
y
4
3
2
1
0
-1
第9题
第10题
10.已知一次函数y=kx+b(k,b是常数,且k≠0)的x与y的部分对应值如下表所示,那么不等式kx+b<0的解集是( )
A.x<0
B.x>0
C.x<2
D.x>2
二、填空题(计20分每题4分)
11.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx.将a,b,c从小到大排列,并用“<”连接为____________.
11题
14题
12.直线y=kx+b与直线y=-x平行,且在y轴上的截距为3,则这条直线的函数表达式为__________.
13.若函数y=kx+3中y随x的增大而减小,则函数y=(1-k)x中y随x的增大而______
14.直线y=kx+b如图10所示,则下列结论:①k>0;②b>0;③k+b>0;④2k+b=0;⑤不等式kx+b<0的解集是x<2.其中正确的结论是________.(填序号)
三、解答题(计60分)
15.(8分)当n取何值时,函数y=(n+2)x+n2-4是正比例函数?是一次函数?
16.(8分)在同一平面直角坐标系中,分别作出下列一次函数的图象:y=-3x,y=-3x+2,y=-3x-2.
(1)这三个函数的图象都是________;
(2)函数y=-3x+2的图象与y轴的交点坐标是____________;
(3)函数y=-3x-2的图象与y轴的交点坐标是____________;
(4)直线y=-3x+2,y=-3x-2分别是由直线y=-3x如何平移得到的?
17.(8分)定义运算“※”为:a※b=
(1)计算:3※4;
(2)画出函数y=2※x的图象.
18.(8分)已知直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过点B作直线BP与x轴相交于点P,且使OP=2OA,求三角形ABP的面积.
(8分)已知正比例函数y=2x和一次函数y=ax+b的图象都经过点A(1,m),且一次函数的图象交x轴于点B(4,0).求一次函数的表达式.
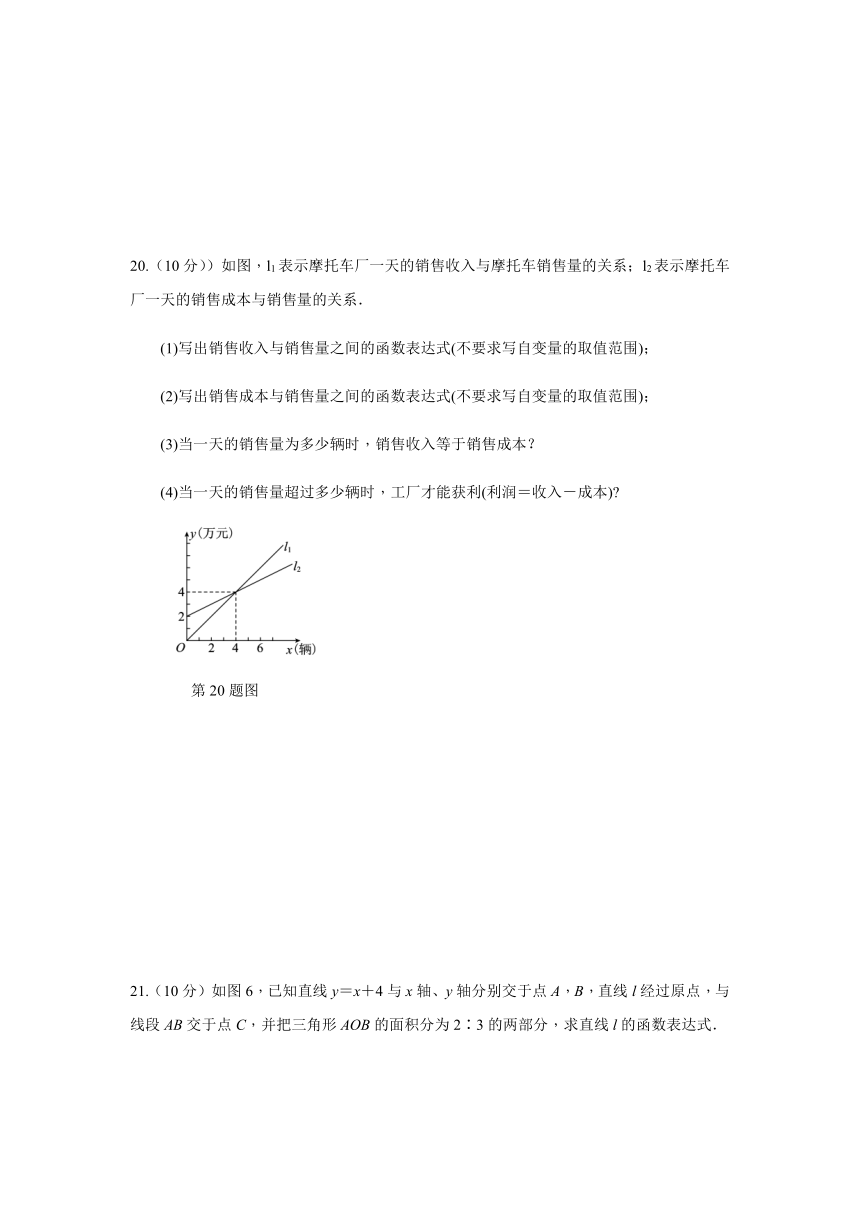
20.(10分))如图,l1表示摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(1)写出销售收入与销售量之间的函数表达式(不要求写自变量的取值范围);
(2)写出销售成本与销售量之间的函数表达式(不要求写自变量的取值范围);
(3)当一天的销售量为多少辆时,销售收入等于销售成本?
(4)当一天的销售量超过多少辆时,工厂才能获利(利润=收入-成本)?
第20题图
21.(10分)如图6,已知直线y=x+4与x轴、y轴分别交于点A,B,直线l经过原点,与线段AB交于点C,并把三角形AOB的面积分为2∶3的两部分,求直线l的函数表达式.
第21题
答案详解
1.[解析]
B 根据一次函数的定义可知(2)(4)是一次函数,(3)分母中含有自变量,不是整式,故不是一次函数,(5)自变量的指数是2,故不是一次函数,(1)
未说明k≠0故选B.
2.D
3.[解析]
D 点A的横坐标为2>0,故点A应在第一象限或第四象限;点B的纵坐标为3>0,故点B应在第一象限或第二象限;由于A,B两点是正比例函数图象上的两点,所以不在同一象限,故点A只能在第四象限,点B只能在第二象限,从而m<0,n<0.故应选D.
4.A
5.[解析]
B 根据一次函数表达式y=x-1中,k>0,可知函数图象经过第一、三象限;根据b=-1<0,可知函数图象经过第四象限.故选B.
6.[解析]
D 因为a-b=1,所以b=a-1.所以y=ax+a-1.因为当x=-1时,y=-a+a-1=-1,所以点(-1,-1)在一次函数y=ax+b的图象上.
7.[解析]
B 因为当x=-1时,y1=-5;当x=4时,y2=10,所以y1<08.[解析]
B 由于直线y=2x-1与y轴的交点是(0,-1),根据点的平移规律,点(0,-1)向左平移1个单位得(-1,-1).由于直线y=2x+b经过点(-1,-1),可知b=1,故平移后的直线为y=2x+1,所以正确选项为B.
9.[解析]
B 设直线AB的函数表达式为y=-2x+b,所以n=-2m+b.所以b=2m+n=6.所以直线AB的函数表达式为y=-2x+6.故选B.
10.[解析]
D 根据表格可以知道当x=2时,y=0,且函数值y随x的增大而减小,故不等式kx+b<0的解集是x>2.故选D.
11.[答案]
a<c<b
12.[答案]
y=-x+3
13.[答案]
增大
14.[答案]
②③④
15.解:若函数y=(n+2)x+n2-4是正比例函数,则根据正比例函数的概念可知n2-4=0且n+2≠0,
所以n=2.
若函数y=(n+2)x+n2-4是一次函数,则n+2≠0,
所以n≠-2.
16.解:图象略.(1)直线 (2)(0,2) (3)(0,-2)
(4)直线y=-3x+2是由直线y=-3x沿y轴向上平移2个单位得到的;直线y=-3x-2是由直线y=-3x沿y轴向下平移2个单位得到的.
17.解:(1)因为4≥0,所以3※4=3×4=12.
(2)当x≥0时,y与x的函数表达式为y=2x;
当x<0时,y与x的函数表达式为y=-2x.
列表如下:
x
…
-2
-1
0
1
2
…
y
…
4
2
0
2
4
…
描点、连线,如图所示.
18.解:(1)令y=0,得x=-,
所以点A的坐标为(-,0).
令x=0,得y=3,所以点B的坐标为(0,3).
(2)设点P的坐标为(x,0),依题意,得x=±3.
所以点P的坐标为P1(3,0)或P2(-3,0),
所以S三角形ABP1=×(+3)×3=,
S三角形ABP2=×(3-)×3=.
所以三角形ABP的面积为或.
19.[解析]
由题意,知正比例函数y=2x的图象过点A(1,m),将(1,m)代入正比例函数表达式y=2x,求出m=2.由题意,知一次函数y=ax+b的图象经过点A(1,2),B(4,0),把两点坐标代入一次函数表达式,根据待定系数法求出一次函数的表达式.
解:由正比例函数y=2x的图象过点A(1,m),
得m=2,所以点A的坐标为(1,2).
由一次函数y=ax+b的图象经过点(1,2)和(4,0),得
解得
所以一次函数的表达式为y=-x+.
20、解:(1)y=x.
(2)设y=kx+b,因为直线过(0,2),(4,4)两点,
所以解得所以y=x+2.
(3)由图象知当x=4时,销售收入等于销售成本;或令x=x+2,解得x=4,即当一天的销售量为4辆时,销售收入等于销售成本.
(4)由图象知当x>4时,工厂才能获利;或令x-(x+2)>0,解得x>4,即当一天的销售量超过4辆时,工厂才能获利.
21.解:设直线l的函数表达式为y=kx.对于y=x+4,当x=0时,y=4;
当y=0时,x=-4,所以A(-4,0),B(0,4).
所以OA=4,OB=4.所以S三角形AOB=×4×4=8.
当直线l把三角形AOB的面积分为S三角形AOC∶S三角形BOC=2∶3时,S△AOC=.
如图,过点C作CF⊥OA于点F,CE⊥OB于点E,
所以AO·CF=,即×4×CF=.
所以CF=.
当y=时,x=-,则=-k.解得k=-.
所以直线l的函数表达式为y=-x.
(时间90分钟
满分120分
)
一、选择题(计40每题4分)
1.有下列函数:(1)y=kx;(2)y=2x-1;(3)y=;(4)y=2-1-3x;(5)y=x2-1.其中是一次函数的有
( )
A.1个
B.2个
C.3个
D.4个
2.如图,直线y=2x必过的点是( )
A.(2,1)
B.(2,2)
C.(-1,-1)
D.(0,0)
如图
3.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
4.将直线y=2x向上平移1个单位,得到的直线的函数表达式为
( )
A.y=2x+1
B.y=2x-1
C.y=2(x+1)
D.y=2(x-1)
5.在平面直角坐标系中,一次函数y=x-1的图象是
( )
6.一次函数y=ax+b中,若a-b=1,则它的图象必经过点( )
A.(1,1)
B.(-1,1)
C.(1,-1)
D.(-1,-1)
7.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
A.0
A.y=2x-2
B.y=2x+1
C.y=2x
D.y=2x+2
9.如图,把直线y=-2x向上平移后得到直线AB,直线AB过点(m,n),且2m+n=6,则直线AB的函数表达式为( )
A.y=-2x+3
B.y=-2x+6
C.y=-2x-3
D.y=-2x-6
x
-2
-1
0
1
2
3
y
4
3
2
1
0
-1
第9题
第10题
10.已知一次函数y=kx+b(k,b是常数,且k≠0)的x与y的部分对应值如下表所示,那么不等式kx+b<0的解集是( )
A.x<0
B.x>0
C.x<2
D.x>2
二、填空题(计20分每题4分)
11.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx.将a,b,c从小到大排列,并用“<”连接为____________.
11题
14题
12.直线y=kx+b与直线y=-x平行,且在y轴上的截距为3,则这条直线的函数表达式为__________.
13.若函数y=kx+3中y随x的增大而减小,则函数y=(1-k)x中y随x的增大而______
14.直线y=kx+b如图10所示,则下列结论:①k>0;②b>0;③k+b>0;④2k+b=0;⑤不等式kx+b<0的解集是x<2.其中正确的结论是________.(填序号)
三、解答题(计60分)
15.(8分)当n取何值时,函数y=(n+2)x+n2-4是正比例函数?是一次函数?
16.(8分)在同一平面直角坐标系中,分别作出下列一次函数的图象:y=-3x,y=-3x+2,y=-3x-2.
(1)这三个函数的图象都是________;
(2)函数y=-3x+2的图象与y轴的交点坐标是____________;
(3)函数y=-3x-2的图象与y轴的交点坐标是____________;
(4)直线y=-3x+2,y=-3x-2分别是由直线y=-3x如何平移得到的?
17.(8分)定义运算“※”为:a※b=
(1)计算:3※4;
(2)画出函数y=2※x的图象.
18.(8分)已知直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过点B作直线BP与x轴相交于点P,且使OP=2OA,求三角形ABP的面积.
(8分)已知正比例函数y=2x和一次函数y=ax+b的图象都经过点A(1,m),且一次函数的图象交x轴于点B(4,0).求一次函数的表达式.
20.(10分))如图,l1表示摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.
(1)写出销售收入与销售量之间的函数表达式(不要求写自变量的取值范围);
(2)写出销售成本与销售量之间的函数表达式(不要求写自变量的取值范围);
(3)当一天的销售量为多少辆时,销售收入等于销售成本?
(4)当一天的销售量超过多少辆时,工厂才能获利(利润=收入-成本)?
第20题图
21.(10分)如图6,已知直线y=x+4与x轴、y轴分别交于点A,B,直线l经过原点,与线段AB交于点C,并把三角形AOB的面积分为2∶3的两部分,求直线l的函数表达式.
第21题
答案详解
1.[解析]
B 根据一次函数的定义可知(2)(4)是一次函数,(3)分母中含有自变量,不是整式,故不是一次函数,(5)自变量的指数是2,故不是一次函数,(1)
未说明k≠0故选B.
2.D
3.[解析]
D 点A的横坐标为2>0,故点A应在第一象限或第四象限;点B的纵坐标为3>0,故点B应在第一象限或第二象限;由于A,B两点是正比例函数图象上的两点,所以不在同一象限,故点A只能在第四象限,点B只能在第二象限,从而m<0,n<0.故应选D.
4.A
5.[解析]
B 根据一次函数表达式y=x-1中,k>0,可知函数图象经过第一、三象限;根据b=-1<0,可知函数图象经过第四象限.故选B.
6.[解析]
D 因为a-b=1,所以b=a-1.所以y=ax+a-1.因为当x=-1时,y=-a+a-1=-1,所以点(-1,-1)在一次函数y=ax+b的图象上.
7.[解析]
B 因为当x=-1时,y1=-5;当x=4时,y2=10,所以y1<0
B 由于直线y=2x-1与y轴的交点是(0,-1),根据点的平移规律,点(0,-1)向左平移1个单位得(-1,-1).由于直线y=2x+b经过点(-1,-1),可知b=1,故平移后的直线为y=2x+1,所以正确选项为B.
9.[解析]
B 设直线AB的函数表达式为y=-2x+b,所以n=-2m+b.所以b=2m+n=6.所以直线AB的函数表达式为y=-2x+6.故选B.
10.[解析]
D 根据表格可以知道当x=2时,y=0,且函数值y随x的增大而减小,故不等式kx+b<0的解集是x>2.故选D.
11.[答案]
a<c<b
12.[答案]
y=-x+3
13.[答案]
增大
14.[答案]
②③④
15.解:若函数y=(n+2)x+n2-4是正比例函数,则根据正比例函数的概念可知n2-4=0且n+2≠0,
所以n=2.
若函数y=(n+2)x+n2-4是一次函数,则n+2≠0,
所以n≠-2.
16.解:图象略.(1)直线 (2)(0,2) (3)(0,-2)
(4)直线y=-3x+2是由直线y=-3x沿y轴向上平移2个单位得到的;直线y=-3x-2是由直线y=-3x沿y轴向下平移2个单位得到的.
17.解:(1)因为4≥0,所以3※4=3×4=12.
(2)当x≥0时,y与x的函数表达式为y=2x;
当x<0时,y与x的函数表达式为y=-2x.
列表如下:
x
…
-2
-1
0
1
2
…
y
…
4
2
0
2
4
…
描点、连线,如图所示.
18.解:(1)令y=0,得x=-,
所以点A的坐标为(-,0).
令x=0,得y=3,所以点B的坐标为(0,3).
(2)设点P的坐标为(x,0),依题意,得x=±3.
所以点P的坐标为P1(3,0)或P2(-3,0),
所以S三角形ABP1=×(+3)×3=,
S三角形ABP2=×(3-)×3=.
所以三角形ABP的面积为或.
19.[解析]
由题意,知正比例函数y=2x的图象过点A(1,m),将(1,m)代入正比例函数表达式y=2x,求出m=2.由题意,知一次函数y=ax+b的图象经过点A(1,2),B(4,0),把两点坐标代入一次函数表达式,根据待定系数法求出一次函数的表达式.
解:由正比例函数y=2x的图象过点A(1,m),
得m=2,所以点A的坐标为(1,2).
由一次函数y=ax+b的图象经过点(1,2)和(4,0),得
解得
所以一次函数的表达式为y=-x+.
20、解:(1)y=x.
(2)设y=kx+b,因为直线过(0,2),(4,4)两点,
所以解得所以y=x+2.
(3)由图象知当x=4时,销售收入等于销售成本;或令x=x+2,解得x=4,即当一天的销售量为4辆时,销售收入等于销售成本.
(4)由图象知当x>4时,工厂才能获利;或令x-(x+2)>0,解得x>4,即当一天的销售量超过4辆时,工厂才能获利.
21.解:设直线l的函数表达式为y=kx.对于y=x+4,当x=0时,y=4;
当y=0时,x=-4,所以A(-4,0),B(0,4).
所以OA=4,OB=4.所以S三角形AOB=×4×4=8.
当直线l把三角形AOB的面积分为S三角形AOC∶S三角形BOC=2∶3时,S△AOC=.
如图,过点C作CF⊥OA于点F,CE⊥OB于点E,
所以AO·CF=,即×4×CF=.
所以CF=.
当y=时,x=-,则=-k.解得k=-.
所以直线l的函数表达式为y=-x.
