青岛版七年级数学上册2.2数轴课件(共33张PPT)
文档属性
| 名称 | 青岛版七年级数学上册2.2数轴课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 860.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-03 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
2.2
数轴
整数(integer)和分数(fraction)统称有理数(rational
number)
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
上节知识回顾
一、
引入
观察图1~4的温度计,回答下列问题
A
B
C
(1)点A表示多少摄氏度,点B呢?点C呢?
(2)A、B、C三点表示的温度哪个高?哪个低?
(3)为何温度计可以表示温度
(因为它有一个“0”刻度,单位长度,一方向为正)
归纳:
一般地,在数学中人们用画图的方式把数“直观化”.
这种直线叫数轴
通常用一条直线上的点表示数.
数轴的三要素
(1)
在直线上任取一点表示0,这个点叫原点;
(2)
通常规定直线上从原点向右(或上)为正方向,从原点想左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3…
原点
正方向
单位长度
数轴满足以下三个条件:
活动1
:画数轴
第一步:画一条直线
第二步:画正方向
第三步:定原点
第四步:定单位长度
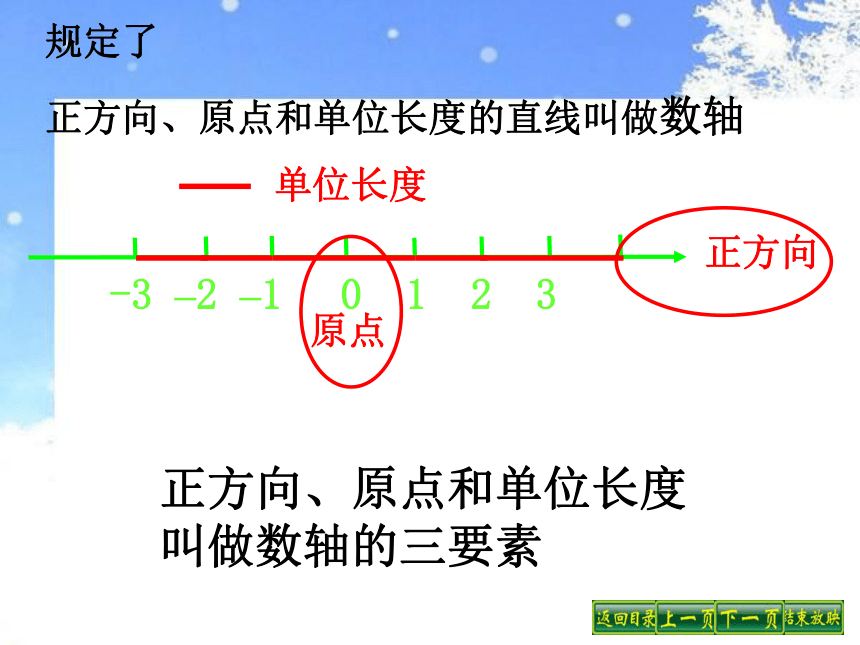
规定了
正方向、原点和单位长度的直线叫做数轴
-3
–2
–1
0
1
2
3
原点
正方向
正方向、原点和单位长度叫做数轴的三要素
单位长度
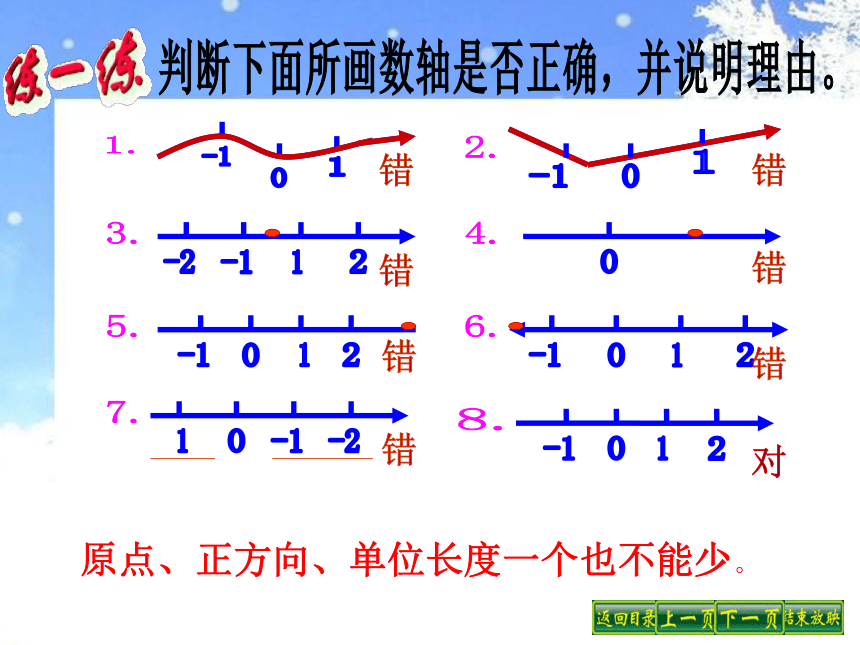
判断下面所画数轴是否正确,并说明理由。
1.
0
1
-1
错
2.
4.
6.
3.
7.
5.
8.
-1
0
1
错
2
-1
-2
1
错
0
错
2
-1
1
0
2
-1
0
错
错
0
错
1
-1
0
1
1
-1
2
对
-2
原点、正方向、单位长度一个也不能少。
下列图形哪些是数轴,哪些不是,为什么?
(E)
(F)
(D)
???再强化概念,深入理解
(A)
(C)
(B)
分数或小数可以用数轴表示吗?
1.5
0.5
-3.5
活动2: 画一条数轴用数轴上的点表示有理数,并注上A、B、C、D、E,怎么找?
-2,
+2,
0,
5,
-
4
活动3:
在数轴上找出分数4.5和
的点,怎么找?
活动4:
在画的数轴上能找出表示100和1/100的点吗?
活动5:
观察数轴上表示正数的点有什么特征?表示负数的点呢?与原点的距离分别是多少?得出了什么结论?
活动4
1、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.
0
1
2
3
-1
-2
-3
4
-4
一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.
右
a
左
a
活动5
例题1
(1)画
出数轴并表示下列有理数:
(2)写出数轴上点A、B、C、D、E表示的数:
0
1
2
3
-1
-2
-3
4
-4
1.5
-2
2
-2.5
0
0
1
2
3
-1
-2
-3
4
-4
E
A
B
C
D
点A表示0
点B表示-2
点C表示1
点D表示2.5
点E表示-3
在数轴上表示数6的点在原点_______侧,到原点的距离是_______个单位长度,表示数-8的点在原点的______侧,到原点的距离是________个单位长度.表示数6的点到表示数-8的点的距离是_______个单位长度.
右
6
左
8
14
若点A在数轴上原点的左边,则A点表示的数是(
)
A
正数
B
负数
C
整数
B
数轴上到原点距离5个单位长度的点表示的数是(
)
A
+5
B
-5
C
C
下列说法不正确(
)
A、数轴是一条直线
B、数轴上所有的点并不都表示有理数
C、在数轴上表示2和-2的点到原点的距离相等
D、数轴上一定取向右为正方向
D
在数轴上原点及原点左边的点所表示的数是(
)
A、正数
B、负数
C、不是负数
D、不是正数
D
判断以下语句是否正确(对的打“√”,错的打“×”).
(1)规定正方向、单位长度的直线叫做数轴。
(2)规定单位长度的直线叫做数轴。
(3)规定正方向、原点、单位长度的直线
叫做数轴
(×)
(×)
(√)
在数轴上0与3之间(不包括0,3)还有
个数。(
)
A、2个
B、3个
C、4个
D、无数个
D
一个点从数轴的原点开始,先向左移动3个单位长度,再向右移动6个单位长度,这个点最终所对应的数是(
)
A.+6
B.-3
C.+3
D.-9
C
下面是我国5个城市在某一天的最低气温:
比较这一天下列两个城市最低气温的高低(填“高于”
或“低于”):
广州
上
海
上
海
北京
北京
哈尔滨
哈尔滨
武汉
武汉
广
州
高于
高于
高于
低于
低于
(1)
把表示上述5个城市最低气温的数表示
在数轴上
(2)
观察这5个数在数轴上的位置,你能按从低到高的顺序依次排列吗?
-10
-5
O
-15
-20
5
10
越
来
越
大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20
-10
0
5
10
●
●
●
●
●
有理数大小的比较方法:
一、数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大。
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
想一想
有没有最大的有理数?有没有最小的有理数?为什么?
(适合数字多个的情况时用)
-5
-4
-3
-2
-1
0
1
2
3
4
5
●
●
●
●
趁热打铁
?
例1
在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接。
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5
<-3
<0
<4
.
正数都大于零,负数都小于零,正数大于负数。
有理数大小的比较方法:
二、直接比较法:
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
(适合两个数字的比较)
比较下列数的大小,并说明理由:
(1)0.01和0
(2)0和-2
(3)0.001和-10000
0.01>0
0>-2
0.001>-10000
更上一层楼
0
0
-1
1、利用数轴回答:
⑴有没有最大的整数和最小的整数?
⑶有没有最大的负整数和最小的负整数?
答:没有最大的正整数,最小的正整数是1。
答:都没有。
⑵有没有最大的正整数和最小的正整数?
答:最大的负整数是-1,没有最小的负整数。
例3.
利用数轴求大于-9并且小于3.2的整数.
加强练习:
0
a
b
c
(1)有理数a,b,c在数轴上的位置如图所示,
请比较a,b,-c的大小,并用“<”号连接;
2.2
数轴
整数(integer)和分数(fraction)统称有理数(rational
number)
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
上节知识回顾
一、
引入
观察图1~4的温度计,回答下列问题
A
B
C
(1)点A表示多少摄氏度,点B呢?点C呢?
(2)A、B、C三点表示的温度哪个高?哪个低?
(3)为何温度计可以表示温度
(因为它有一个“0”刻度,单位长度,一方向为正)
归纳:
一般地,在数学中人们用画图的方式把数“直观化”.
这种直线叫数轴
通常用一条直线上的点表示数.
数轴的三要素
(1)
在直线上任取一点表示0,这个点叫原点;
(2)
通常规定直线上从原点向右(或上)为正方向,从原点想左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3…
原点
正方向
单位长度
数轴满足以下三个条件:
活动1
:画数轴
第一步:画一条直线
第二步:画正方向
第三步:定原点
第四步:定单位长度
规定了
正方向、原点和单位长度的直线叫做数轴
-3
–2
–1
0
1
2
3
原点
正方向
正方向、原点和单位长度叫做数轴的三要素
单位长度
判断下面所画数轴是否正确,并说明理由。
1.
0
1
-1
错
2.
4.
6.
3.
7.
5.
8.
-1
0
1
错
2
-1
-2
1
错
0
错
2
-1
1
0
2
-1
0
错
错
0
错
1
-1
0
1
1
-1
2
对
-2
原点、正方向、单位长度一个也不能少。
下列图形哪些是数轴,哪些不是,为什么?
(E)
(F)
(D)
???再强化概念,深入理解
(A)
(C)
(B)
分数或小数可以用数轴表示吗?
1.5
0.5
-3.5
活动2: 画一条数轴用数轴上的点表示有理数,并注上A、B、C、D、E,怎么找?
-2,
+2,
0,
5,
-
4
活动3:
在数轴上找出分数4.5和
的点,怎么找?
活动4:
在画的数轴上能找出表示100和1/100的点吗?
活动5:
观察数轴上表示正数的点有什么特征?表示负数的点呢?与原点的距离分别是多少?得出了什么结论?
活动4
1、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.
0
1
2
3
-1
-2
-3
4
-4
一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.
右
a
左
a
活动5
例题1
(1)画
出数轴并表示下列有理数:
(2)写出数轴上点A、B、C、D、E表示的数:
0
1
2
3
-1
-2
-3
4
-4
1.5
-2
2
-2.5
0
0
1
2
3
-1
-2
-3
4
-4
E
A
B
C
D
点A表示0
点B表示-2
点C表示1
点D表示2.5
点E表示-3
在数轴上表示数6的点在原点_______侧,到原点的距离是_______个单位长度,表示数-8的点在原点的______侧,到原点的距离是________个单位长度.表示数6的点到表示数-8的点的距离是_______个单位长度.
右
6
左
8
14
若点A在数轴上原点的左边,则A点表示的数是(
)
A
正数
B
负数
C
整数
B
数轴上到原点距离5个单位长度的点表示的数是(
)
A
+5
B
-5
C
C
下列说法不正确(
)
A、数轴是一条直线
B、数轴上所有的点并不都表示有理数
C、在数轴上表示2和-2的点到原点的距离相等
D、数轴上一定取向右为正方向
D
在数轴上原点及原点左边的点所表示的数是(
)
A、正数
B、负数
C、不是负数
D、不是正数
D
判断以下语句是否正确(对的打“√”,错的打“×”).
(1)规定正方向、单位长度的直线叫做数轴。
(2)规定单位长度的直线叫做数轴。
(3)规定正方向、原点、单位长度的直线
叫做数轴
(×)
(×)
(√)
在数轴上0与3之间(不包括0,3)还有
个数。(
)
A、2个
B、3个
C、4个
D、无数个
D
一个点从数轴的原点开始,先向左移动3个单位长度,再向右移动6个单位长度,这个点最终所对应的数是(
)
A.+6
B.-3
C.+3
D.-9
C
下面是我国5个城市在某一天的最低气温:
比较这一天下列两个城市最低气温的高低(填“高于”
或“低于”):
广州
上
海
上
海
北京
北京
哈尔滨
哈尔滨
武汉
武汉
广
州
高于
高于
高于
低于
低于
(1)
把表示上述5个城市最低气温的数表示
在数轴上
(2)
观察这5个数在数轴上的位置,你能按从低到高的顺序依次排列吗?
-10
-5
O
-15
-20
5
10
越
来
越
大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20
-10
0
5
10
●
●
●
●
●
有理数大小的比较方法:
一、数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大。
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
想一想
有没有最大的有理数?有没有最小的有理数?为什么?
(适合数字多个的情况时用)
-5
-4
-3
-2
-1
0
1
2
3
4
5
●
●
●
●
趁热打铁
?
例1
在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接。
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5
<-3
<0
<4
.
正数都大于零,负数都小于零,正数大于负数。
有理数大小的比较方法:
二、直接比较法:
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
(适合两个数字的比较)
比较下列数的大小,并说明理由:
(1)0.01和0
(2)0和-2
(3)0.001和-10000
0.01>0
0>-2
0.001>-10000
更上一层楼
0
0
-1
1、利用数轴回答:
⑴有没有最大的整数和最小的整数?
⑶有没有最大的负整数和最小的负整数?
答:没有最大的正整数,最小的正整数是1。
答:都没有。
⑵有没有最大的正整数和最小的正整数?
答:最大的负整数是-1,没有最小的负整数。
例3.
利用数轴求大于-9并且小于3.2的整数.
加强练习:
0
a
b
c
(1)有理数a,b,c在数轴上的位置如图所示,
请比较a,b,-c的大小,并用“<”号连接;
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
