人教版八年级数学上册 13.1.1轴对称 同步训练卷(word版含答案)
文档属性
| 名称 | 人教版八年级数学上册 13.1.1轴对称 同步训练卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 448.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 08:08:21 | ||
图片预览



文档简介
人教版八年级数学上册
13.1.1轴对称
同步训练卷
一、选择题(共10小题,3
10=30)
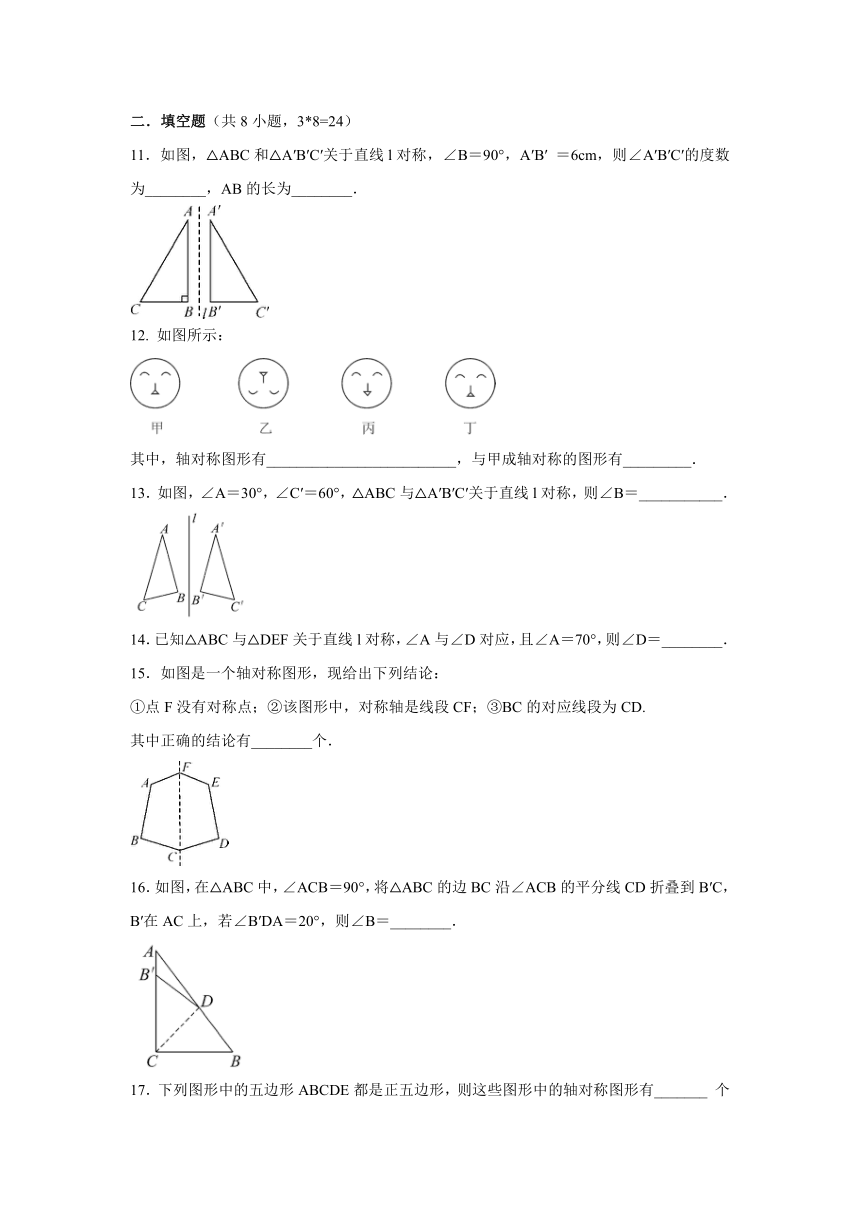
1.在一些美术字中,有的汉字是轴对称图形,下面4个汉字中,可以看作是轴对称图形的是( )
2.下列倡导节约的图案中,是轴对称图形的是( )
3.篆刻是中国独特的传统艺术,篆刻出来的艺术品叫印章.印章的文字刻成凸状的称为“阳文”,刻成凹状的称为“阴文”.如图所示的“希望”即为阳文印章在纸上盖出的效果,此印章是下列选项中的(阴影表示印章中的实体部分,白色表示印章中的镂空部分)( )
4.下列各组图中,左右两个图形成轴对称的是( )
5.下图均由正六边形与两条对角线所组成,其中不是轴对称图形的是( )
6.
如图,右边图形与左边图形成轴对称的有( )
A.1组
B.2组
C.3组
D.4组
7.如图,关于虚线成轴对称的有( )
A.1个
B.2个
C.3个
D.4个
8.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定成立的是( )
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
9.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
10.国际数学家大会的会标如图1所示,把这个图案沿图中线段剪开后,能拼成如图2所示的四个图形,则其中是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,3
8=24)
11.如图,△ABC和△A′B′C′关于直线l对称,∠B=90°,A′B′
=6cm,则∠A′B′C′的度数为________,AB的长为________.
12.
如图所示:
其中,轴对称图形有_________________________,与甲成轴对称的图形有_________.
13.如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B=___________.
14.已知△ABC与△DEF关于直线l对称,∠A与∠D对应,且∠A=70°,则∠D=________.
15.如图是一个轴对称图形,现给出下列结论:
①点F没有对称点;②该图形中,对称轴是线段CF;③BC的对应线段为CD.
其中正确的结论有________个.
16.如图,在△ABC中,∠ACB=90°,将△ABC的边BC沿∠ACB的平分线CD折叠到B′C,B′在AC上,若∠B′DA=20°,则∠B=________.
17.下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有_______
个
18.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为__________.
三.解答题(共7小题,
46分)
19.(6分)
如图所示,已知点A是锐角∠MON内的一点,试分别在OM、ON上确定点B、点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点.(要求画出草图,保留作图痕迹)
20.(6分)
已知在△ABC中,AD⊥BC于点D,AC的垂直平分线分别交BC,AC于点E,F,已知AE=AB,则AB,BD,DC三者之间有怎样的数量关系?说明理由.
21.(6分)
如图,BD=DC,ED⊥BC,AE平分∠BAC,EM⊥AB,EN⊥AC垂足分别为M,N。求证:BM=CN。
22.(6分)
如图,点P在∠AOB内,M,N分别是点P关于AO,BO的对称点,MN分别交AO,BO于点E,F,若△PEF的周长等于20
cm,求MN的长.
23.(6分)
在△ABC中,∠C=90°,DE垂直平分斜边AB,且分别交AB、BC于D、E,若∠CAE=∠B+30°,求∠AEB的度数。
24.(8分)
如图,△ABC与△DEF关于直线MN对称,其中∠C=90°,AC=8
cm,DE=10
cm,BC=6
cm.
(1)线段AD与MN的关系是什么?
(2)求∠F的度数;
求△ABC的周长.
25.(8分)
如图,已知△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)若直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹角α的数量关系.
参考答案
1-5ACDAD
6-10BCBBC
11.
90°,6
cm
12.
甲、乙、丙、丁,丁
13.
90°
14.
70°
15.
1
16.
55°
17.
4
18.
112°
19.
解:分别作点A关于OM、ON的对称点A'、A";连A'A",分别交OM、ON于点B、点C,则点B、点C即为所求,作图如图所示.
20.
解:AB+BD=DC.
理由:∵AB=AE,AD⊥BC,∴BD=DE,
∵点E在AC的垂直平分线上,
∴AE=CE,∴AB=CE,
∴AB+BD=CE+DE=DC,即AB+BD=DC.
21.
证明:连接BE,CE,
因为BD=DC、ED⊥BC,所以EB=EC,
又因为EM⊥AB,EN⊥AC,EA平分∠BAC,
所以EM=EN,∠EMB=∠ENC=90度,
所以RT△BEM≌RT△CEN,
所以BM=CN
22.
解:∵M,N分别是点P关于AO,BO的对称点,
∴ME=PE,PF=NF.
又∵△PEF的周长为20
cm,
即PE+EF+PF=20
cm.
∴ME+EF+FN=20
cm,
即MN=20
cm.
23.
解:∵DE垂直平分斜边AB,∴AE=BE,∴∠B=∠EAB。∵∠C=90°,
∴∠CAB+∠B=90°。又∵∠CAE=∠B+30°,
∴∠B+30°+∠B+∠B=90°
∴∠B=20°
∴∠AEB=180°-∠EAB-∠B=180°-20°-20°=140°。
24.
解:(1)∵△ABC与△DEF关于直线MN对称,∴MN垂直平分AD.
(2)∵△ABC与△DEF关于直线MN对称,∴△ABC≌△DEF.
∴∠C=∠F=90°.
(3)∵AC=8
cm,DE=10
cm,BC=6
cm,
∴DE=AB=10
cm.
∴△ABC的周长为6+8+10=24(cm).
解:(1)如图,连接B′B″,画线段B′B″的垂直平分线EF,则直线EF是△A′B′C′和△A″B″C″的对称轴.
(2)如图,连接B′O.
∵△ABC和△A′B′C′关于直线MN对称,∴∠BOM=∠B′OM.
∵△A′B′C′和△A″B″C″关于直线EF对称,∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=
2(∠B′OM+∠B′OE)=2∠MOE,
即∠BOB″=2α.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
13.1.1轴对称
同步训练卷
一、选择题(共10小题,3
10=30)
1.在一些美术字中,有的汉字是轴对称图形,下面4个汉字中,可以看作是轴对称图形的是( )
2.下列倡导节约的图案中,是轴对称图形的是( )
3.篆刻是中国独特的传统艺术,篆刻出来的艺术品叫印章.印章的文字刻成凸状的称为“阳文”,刻成凹状的称为“阴文”.如图所示的“希望”即为阳文印章在纸上盖出的效果,此印章是下列选项中的(阴影表示印章中的实体部分,白色表示印章中的镂空部分)( )
4.下列各组图中,左右两个图形成轴对称的是( )
5.下图均由正六边形与两条对角线所组成,其中不是轴对称图形的是( )
6.
如图,右边图形与左边图形成轴对称的有( )
A.1组
B.2组
C.3组
D.4组
7.如图,关于虚线成轴对称的有( )
A.1个
B.2个
C.3个
D.4个
8.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定成立的是( )
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
9.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
10.国际数学家大会的会标如图1所示,把这个图案沿图中线段剪开后,能拼成如图2所示的四个图形,则其中是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,3
8=24)
11.如图,△ABC和△A′B′C′关于直线l对称,∠B=90°,A′B′
=6cm,则∠A′B′C′的度数为________,AB的长为________.
12.
如图所示:
其中,轴对称图形有_________________________,与甲成轴对称的图形有_________.
13.如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B=___________.
14.已知△ABC与△DEF关于直线l对称,∠A与∠D对应,且∠A=70°,则∠D=________.
15.如图是一个轴对称图形,现给出下列结论:
①点F没有对称点;②该图形中,对称轴是线段CF;③BC的对应线段为CD.
其中正确的结论有________个.
16.如图,在△ABC中,∠ACB=90°,将△ABC的边BC沿∠ACB的平分线CD折叠到B′C,B′在AC上,若∠B′DA=20°,则∠B=________.
17.下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有_______
个
18.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为__________.
三.解答题(共7小题,
46分)
19.(6分)
如图所示,已知点A是锐角∠MON内的一点,试分别在OM、ON上确定点B、点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点.(要求画出草图,保留作图痕迹)
20.(6分)
已知在△ABC中,AD⊥BC于点D,AC的垂直平分线分别交BC,AC于点E,F,已知AE=AB,则AB,BD,DC三者之间有怎样的数量关系?说明理由.
21.(6分)
如图,BD=DC,ED⊥BC,AE平分∠BAC,EM⊥AB,EN⊥AC垂足分别为M,N。求证:BM=CN。
22.(6分)
如图,点P在∠AOB内,M,N分别是点P关于AO,BO的对称点,MN分别交AO,BO于点E,F,若△PEF的周长等于20
cm,求MN的长.
23.(6分)
在△ABC中,∠C=90°,DE垂直平分斜边AB,且分别交AB、BC于D、E,若∠CAE=∠B+30°,求∠AEB的度数。
24.(8分)
如图,△ABC与△DEF关于直线MN对称,其中∠C=90°,AC=8
cm,DE=10
cm,BC=6
cm.
(1)线段AD与MN的关系是什么?
(2)求∠F的度数;
求△ABC的周长.
25.(8分)
如图,已知△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)若直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹角α的数量关系.
参考答案
1-5ACDAD
6-10BCBBC
11.
90°,6
cm
12.
甲、乙、丙、丁,丁
13.
90°
14.
70°
15.
1
16.
55°
17.
4
18.
112°
19.
解:分别作点A关于OM、ON的对称点A'、A";连A'A",分别交OM、ON于点B、点C,则点B、点C即为所求,作图如图所示.
20.
解:AB+BD=DC.
理由:∵AB=AE,AD⊥BC,∴BD=DE,
∵点E在AC的垂直平分线上,
∴AE=CE,∴AB=CE,
∴AB+BD=CE+DE=DC,即AB+BD=DC.
21.
证明:连接BE,CE,
因为BD=DC、ED⊥BC,所以EB=EC,
又因为EM⊥AB,EN⊥AC,EA平分∠BAC,
所以EM=EN,∠EMB=∠ENC=90度,
所以RT△BEM≌RT△CEN,
所以BM=CN
22.
解:∵M,N分别是点P关于AO,BO的对称点,
∴ME=PE,PF=NF.
又∵△PEF的周长为20
cm,
即PE+EF+PF=20
cm.
∴ME+EF+FN=20
cm,
即MN=20
cm.
23.
解:∵DE垂直平分斜边AB,∴AE=BE,∴∠B=∠EAB。∵∠C=90°,
∴∠CAB+∠B=90°。又∵∠CAE=∠B+30°,
∴∠B+30°+∠B+∠B=90°
∴∠B=20°
∴∠AEB=180°-∠EAB-∠B=180°-20°-20°=140°。
24.
解:(1)∵△ABC与△DEF关于直线MN对称,∴MN垂直平分AD.
(2)∵△ABC与△DEF关于直线MN对称,∴△ABC≌△DEF.
∴∠C=∠F=90°.
(3)∵AC=8
cm,DE=10
cm,BC=6
cm,
∴DE=AB=10
cm.
∴△ABC的周长为6+8+10=24(cm).
解:(1)如图,连接B′B″,画线段B′B″的垂直平分线EF,则直线EF是△A′B′C′和△A″B″C″的对称轴.
(2)如图,连接B′O.
∵△ABC和△A′B′C′关于直线MN对称,∴∠BOM=∠B′OM.
∵△A′B′C′和△A″B″C″关于直线EF对称,∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=
2(∠B′OM+∠B′OE)=2∠MOE,
即∠BOB″=2α.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
