人教版九年级数学上册 第二十三章 旋转 23.1 图形的旋转 课后练习(word版含答案)
文档属性
| 名称 | 人教版九年级数学上册 第二十三章 旋转 23.1 图形的旋转 课后练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 491.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 08:40:01 | ||
图片预览




文档简介
人教版九年级数学上册
第二十三章
旋转
23.1
图形的旋转
课后练习
一、单选题
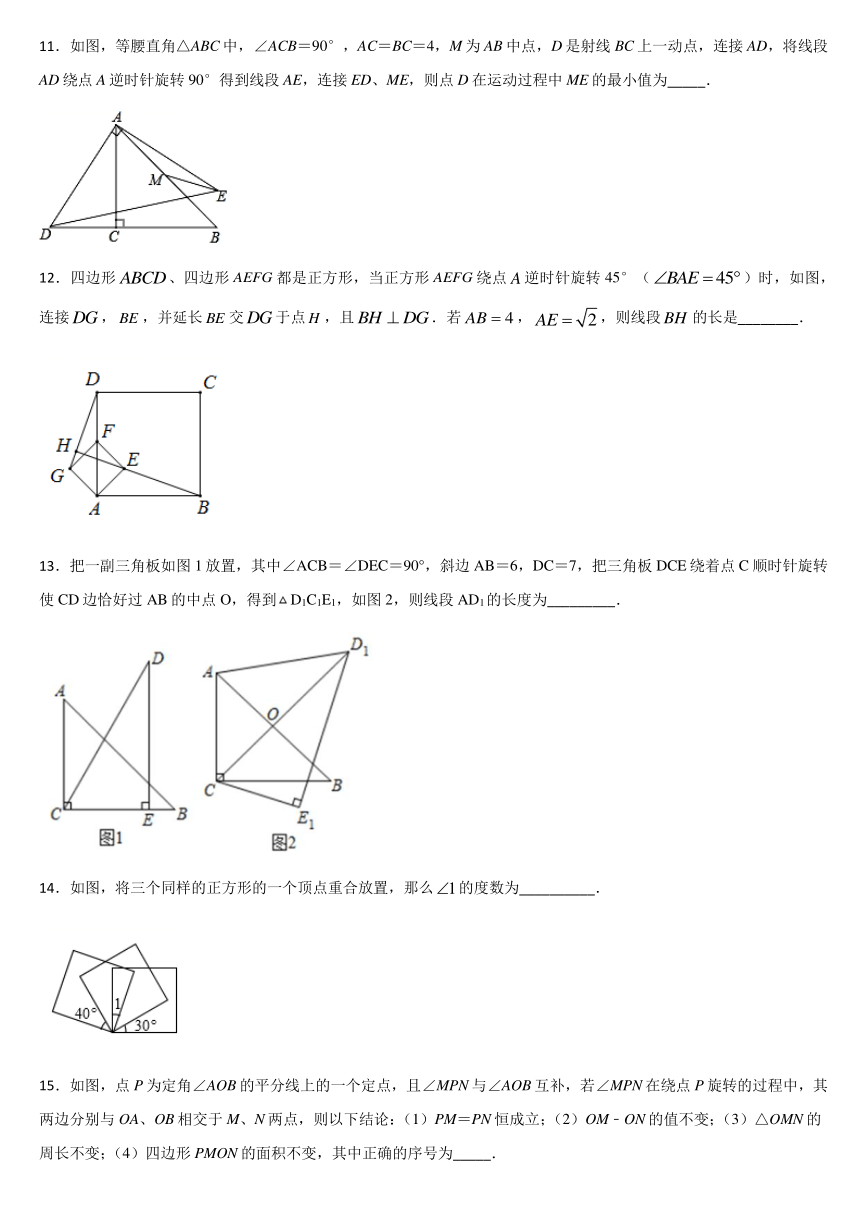
1.如图,菱形OABC的顶点O(0,0),A(﹣2,0),∠B=60°,若菱形绕点O顺时针旋转90°后得到菱形OA1B1C1,依此方式,绕点O连续旋转2020次得到菱形OA2020B2020C2020,那么点C2020的坐标是(
)
A.(,1)
B.(1,﹣)
C.(﹣,﹣1)
D.(﹣1,)
2.如图,△ABC中,∠BAC=90°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1,点C的对应点恰好落在CB的延长线上,连接CB1,则下列说法错误的是( )
A.旋转角为120°
B.ABB1C1
C.S=S
D.AB1=B1C1
3.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形,图中阴影部分的面积为(
)
A.a2
B.a2
C.(1﹣)a2
D.(1﹣)a2
4.如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为(
)
A.3
B.2.5
C.4
D.2
5.如图,在正方形内作,交于点,交于点,连接,过点作,垂足为点,将绕点顺时针旋转得到,若,则以下结论:①,②,③,④,正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
6.如图,等边三角形的边长为4,点是△的中心,.绕点旋转,分别交线段于两点,连接,给出下列四个结论:①;②;③四边形的面积始终等于;④△周长的最小值为6,上述结论中正确的个数是(
)
A.1
B.2
C.3
D.4
7.如图,在坐标系中放置一菱形
OABC,已知∠ABC=60°,点
B
在
y
轴上,OA=1,先将菱形
OABC
沿
x
轴的正方向无滑动翻转,每次翻转
60°,连续翻转2019次,点
B
的落点依次为
B1,B2,B3,…,则
B2
019
的坐标为(
)
A.(1010,0)
B.(1310.5,
)
C.(1345,
)
D.(1346,0)
8.如图,长方形ABCD的顶点A、B分别在x轴、y轴上,OA=OB=2,AD=4,将长方形ABCD绕点O顺时针旋转,每次旋转90°,则第2021次旋转结束时,点C的坐标为(
)
A.(6,4)
B.(4,6)
C.(-6,4)
D.(-4,6)
9.如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A.
B.
C.
D.1
10.已知正方形ABCD的边长为2,正方形内有一动点P,求点P到三个顶点A、B、C的距离之和的最小值(
)
A.
B.
C.
D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,等腰直角△ABC中,∠ACB=90°,AC=BC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,则点D在运动过程中ME的最小值为_____.
12.四边形、四边形都是正方形,当正方形绕点逆时针旋转45°()时,如图,连接,,并延长交于点,且.若,,则线段的长是________.
13.把一副三角板如图1放置,其中∠ACB=∠DEC=90°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转使CD边恰好过AB的中点O,得到D1C1E1,如图2,则线段AD1的长度为_________.
14.如图,将三个同样的正方形的一个顶点重合放置,那么的度数为__________.
15.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM﹣ON的值不变;(3)△OMN的周长不变;(4)四边形PMON的面积不变,其中正确的序号为_____.
三、解答题
16.如图,四边形ABCD是正方形,点E是BC边上的动点(不与点B、C重合),将射线AE绕点A按逆时针方向旋转45°后交CD边于点F,AE、AF分别交BD于G、H两点.
(1)当∠BEA=55°时,求∠HAD的度数;
(2)设∠BEA=α,试用含α的代数式表示∠DFA的大小;
(3)点E运动的过程中,试探究∠BEA与∠FEA有怎样的数量关系,并说明理由.
17.如图,在梯形ABCD中,ABCD,∠BAD=90°,∠1=∠2=60°.射线AM以每秒2°的速度绕着端点A顺时针旋转至AB处停止,同时射线CN以每秒1°的速度绕端点C顺时针旋转至CD处停止.
(1)射线AM、CN旋转30秒时,∠DAM=
度,∠BCN=
度;
(2)若射线CN先转动80秒,射线AM才开始转动,如图2,当射线AM与射线CN相交所形成的∠AEC=150°时,求射线AM的旋转时间.
(3)如图3,若射线AM、CN同时转动,在射线AM到达AB之前与射线CN交于点E,以点E为顶点作∠AEF交DC的延长线于点F,且∠AEF=130°,请探究此时∠CAE与∠CEF的数量关系,并说明理由.
18.书籍和纸张的长与宽比值都有固定的尺寸,如常用的A3、A4、A5的纸张长与宽的比值都相等.一长方形纸张对折后的小长方形的长与宽的比值与原长方形的长与宽的比值相等.
(1)求满足这样条件的长方形的长与宽的比值;
(2)如图所示的长方形ABCD长与宽之比也满足以上条件,其中宽AB=2.
①点P是AD上一点,将△BPA沿BP折叠得到△BPE,当BE垂直AC时,求AP的长;
②若将长方形ABCD绕点B旋转得到长方形A1BC1D1,直线CC1交DD1于点M,N为BC的中点,直接写出MN的最大值:
.
19.综合与探究
如图,点是等边内一点,将绕点按顺时针方向旋转得到,连接和.
(1)求证:是等边三角形;
(2)若,,,求的长;
(3)若,则_________度时,是等腰三角形?(直接写出答案).
20.的边BC=,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB=
度;
(2)如图,将绕点C顺时针旋转60°,画出旋转后的图形;
(3)AP+BP+CP的最小值为
.
21.如图1,△ABC是等腰直角三角形,AB=BC,∠ABC=90°,线段BD可绕点B在平面内旋转,BD=4.
(1)若AB=8,在线段BD旋转过程中,当点B,C,D三点在同一直线上时,直接写出CD的长.
(2)如图2,若将线段BD绕点B按顺时针方向旋转90°,得到线段BE,连接AE,CE.
①当点D的位置由△ABC外的点D转到其内的点E处,且∠AEB=135°,AE=2时,求CE的长;
②如图3,若AB=8,连接DE,将△BDE绕点B在平面内旋转,分别取DE,AE,AC的中点M,P,N,连接MP,PN,NM,请直接写出△MPN面积S的取值范围.
22.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
23.(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取到最大值,且最大值为 ;(用含a、b的式子表示).
(2)如图2,若点A为线段BC外一动点,且BC=6,AB=3,分别以AB,AC为边,作等边△ABD和等边△ACE,连接CD,BE.
①图中与线段BE相等的线段是线段 ,并说明理由;
②直接写出线段BE长的最大值为 .
(3)如图3,在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(10,0),点P为线段AB外一动点,且PA=4,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值为 ,及此时点P的坐标为 .
(提示:等腰直角三角形的三边长a、b、c满足a:b:c=1:1:)
【参考答案】
1.D
2.D
3.D
4.C
5.C
6.C
7.D
8.A
9.A
10.C
11.2.
12.
13.5
14.20°.
15.(1)(4)
16.解:(1)∵四边形ABCD是正方形,
∴∠EBA=∠BAD=90°,
∴∠EAB=90°﹣∠BAE=90°﹣55°=35°,
∴∠HAD=∠BAD﹣∠EAF﹣∠EAB=90°﹣45°﹣35°=10°;
(2)∵四边形ABCD是正方形,
∴∠EBA=∠BAD=∠ADF=90°,
∴∠EAB=90°﹣∠BAE=90°﹣α,
∴∠DAF=∠BAD﹣∠EAF﹣∠EAB=,
∴∠DFA=90°﹣∠DAF==135°﹣α;
(3)∠BEA=∠FEA,理由如下:
延长CB至I,使BI=DF,连接AI.
∵四边形ABCD是正方形,
∴AD=AB,∠ADF=∠ABC=90°,
∴∠ABI=90°,
又∵BI=DF,
∴△DAF≌△BAI(SAS),
∴AF=AI,∠DAF=∠BAI,
∴∠EAI=∠BAI+∠BAE=∠DAF+∠BAE=45°=∠EAF,
又∵AE是△EAI与△EAF的公共边,
∴△EAI≌△EAF(SAS),
∴∠BEA=∠FEA.
17.解:(1)∵射线AM以每秒2°的速度绕着端点A顺时针旋转,射线CN以每秒1°的速度绕端点C顺时针旋转,
∴射线AM、CN旋转30秒时,∠DAM=30×2°=60°,∠BCN=30×1°=30°,
故答案为60,30;
(2)根据题意画出图形如图2:
∵在梯形ABCD中,AB∥CD,∠BAD=90°,∠1=∠2=60°.
∴∠CAB=30°,
∴∠ACB=90°,
设射线AM的旋转时间为x秒,则射线CN旋转的时间为(80+x)秒,
∴∠MAM′=2x,∠NCN′=80+x,
∴∠CAM′=∠1﹣∠MAM′=60﹣2x,ACN′=80+x﹣90=x﹣10,
∵∠AEC=150°,
∴60﹣2x+x﹣10+150=180,
解得x=20,
即射线AM的旋转时间为20秒;
(3)∠CAE=2∠CEF﹣20°,
理由:设射线转动时间为t秒,如图3,
∵∠DAE=2t,
∴∠CAE=2t﹣60°,
又∵∠BCE=t,
∴∠ACE=90°﹣t,
∴∠AEC=180°﹣∠CAE﹣∠ACE=150°﹣t,而∠AEF=130°,
∴∠CEF=130°﹣∠AEC=130°﹣(150°﹣t)=t﹣20°,
∴∠CAE=2∠CEF﹣20°.
18.(1)设长方形的长与宽分别为a,b.
由题意:,
∴a2=2b2,
∴;
(2)①如图1中,延长PE、BC交于点G,
∵∠PEB=90°,
∴PE⊥BE,
∵BE⊥AC,BE⊥PE,
∴PG∥AC,
∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=2,AD∥BG,∠ABC=90°,
∴四边形APGC是平行四边形,
∴PG=AC===2,
∵AD∥BC,
∴∠APB=∠GBP,
∵∠APB=∠GPB,
∴∠GBP=∠GPB,
∴GP=GB=2,
∴AP=CG=BG=BC=2﹣2;
②如图2中,连接BM,取BD的中点O,连接OM,ON,延长CC1到K,使得C1K=CC1在MK的延长线上取一点J,使得D1J=D1K,连接BD1.
∵BC=BC1,
∴∠BCC1=∠BC1C,
∵∠BC1D1=∠BCD=90°,
∴∠D1C1K+∠BC1C=90°,∠BCC1+∠DCC1=90°,
∴∠D1C2K=∠DCC1,
∵CD=C1D1,CC1=C1K,
∴△DCC1≌△D1C1K(SAS),
∴DC1=KD1=JD1,∠CC1D=∠C1KD1,
∵∠JKD1+∠C1JKD1=180°,∠CC1D+∠DC1M=180°,
∴∠DC1M=∠D1KJ,
∵D1J=D1K,
∴∠J=∠D1KJ,
∴∠J=∠DC1M,
∵∠D1MJ=∠DMC1,
∴△D1MJ≌△DMC1(AAS),
∴D1M=DM′,
∵BD=BD1,
∴BM⊥DD1,
取BD的中点O,连接OM,ON,
∵∠BMD=90°,
∴OM=BD=,
∵BO=OD,BN=CN,
∴ON=CD=1,
∵MN≤OM+ON,
∴MN≤+1,
∴MN的最大值为+1.
故答案为:+1.
19.(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)解:由(1)知△COD是等边三角形;
∴
OD=OC=4,∠ODC=60°,
∵
将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴AD=OB=3,∠ADC=∠BOC=150°,
∴∠ADO=∠ADC-∠ODC=90°,
∴OA=;
(3)解:设∠BOC=α,
①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠OAD=180°-(∠AOD+∠ADO)=180°-(190°-α+α-60°)=50°,
∴α-60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵∠AOD=360°-110°-60°-α=190°-α,
∠OAD==120°-
∴190°-α=120°-,
解得α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
故答案为:125或110或140.
20.(1)∵点A在BC的垂直平分线上,
∴AB=AC,
∴∠ACB=∠ABC=30°,
故答案为:30;
(2)如图:
(3)如图,连接、AB、A,
由旋转得AP=A,PC=C,AC=C,∠AC=∠PC=60°,
∴△PC、△AC都是等边三角形,
∴PC=P,∠AC=60°,
∵∠ACB=∠ABC=30°,
∴∠AC=∠ACB+∠ABC,即B、A、三点共线,
∵∠CB=∠CA+∠ACB=90°,∠BC=60°,BC=,
∴B=,
当B、P、、四点共线时,AP+BP+CP=PB++A值的最小,
∴AP+BP+CP=B=4,
故答案为:4.
21.解:(1)当点D在CB的延长线上时,CD=4+8=12,
当点D在线段BC上时,CD=8﹣4=4,
故CD的长为4或12.
(2)①如图2中,连接AD,DE.
∵BD=BE=4,∠DBE=90°,
∴,∠DEB=45°,
∵∠AEB=135°,
∴∠AED=90°,
∵,
∴
∵∠DBE=∠ABC=90°,
∴∠DBA=∠EBC,
∵BD=BE,BA=BC,
∴△DBA≌△EBC(SAS),
∴.
②如图3中,连接AD,延长CE交AB于O,交AD于J.
∵∠DBE=∠ABC=90°,
∴∠DBA=∠EBC,
∵BD=BE,BA=BC,
∴△DBA≌△EBC(SAS),
∴EC=AD,∠DAB=∠ECB,
∵∠BOC+∠BCE=90°,∠AOJ=∠BOC,
∴∠AOJ+∠DAB=90°,
∴∠AJC=90°,
∴CJ⊥AD,
∵AP=EP,EM=MD,
∴PM∥AD,,
同法可得,PN∥EC,,
∴PM=PN,PM⊥JC,
∴PN⊥PM,
∴△PMN是等腰直角三角形,
∴
∵4≤AD≤12,
∴2≤S△PMN≤18.
22.证明:(1)∵将线段AD绕点A逆时针旋转60°得到线段AE
∴AD=AE,∠DAE=60°
∴△ADE是等边三角形
∵△ABC为等边三角形
∴AB=AC,
∠BAC=∠DAE=60°
∴∠DAB=∠CAE,且AB=AC,AD=AE
∴△ADB≌△AEC(SAS)
∴BD=CE
(2)如图,过点C作CG∥BP,交EF的延长线于点G
∵∠ADB=90°,
∠ADE=60°
∴∠BDG=30°
∵CG∥BP
∴∠G=∠BDG=30°
∵△ADB≌△AEC
∴BD=CE,∠ADB=∠AEC=90°
∴∠GEC=∠AEC﹣∠AED=30°
∴∠G=∠GEC=30°
∴GC=CE
∴CG=BD,且∠BDG=∠G,
∠BFD=∠GFC
∴△BFD≌△CFG(AAS)
∴BF=FC
∴点F是BC中点
(3)如图,连接AF,
∵△ABC是等边三角形,BF=FC
∴AF⊥BC
∴∠AFC=90°
∴∠AFC=∠AEC=90°
∴点A,点F,点C,点E四点在以AC为直径的圆上
∴EF最大为直径,
即最大值为1
23.(1)∵点A为线段BC外一动点,且BC=a,AB=b,
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.
故答案为:CB的延长线上,a+b;
(2)①CD=BE,
理由:∵△ABD与△ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB.
在△CAD与△EAB中,
,
∴△CAD≌△EAB(SAS),
∴CD=BE.
故答案是:CD;
②∵线段BE长的最大值=线段CD的最大值,
由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,
∴最大值为BD+BC=AB+BC=9.
故答案为:CD=BE=9.
(3)如图1,
∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,
则△APN是等腰直角三角形,
∴PN=PA=2,BN=AM.
∵A的坐标为(4,0),点B的坐标为(10,0),
∴OA=4,OB=10,∴AB=6,
∴线段AM长的最大值=线段BN长的最大值,
∴当N在线段BA的延长线时,线段BN取得最大值,
最大值=AB+AN.
∵ANAP=4,
∴最大值为46.
如图2,
过P作PE⊥x轴于E.
∵△APN是等腰直角三角形,
∴PE=AE=2,
∴OE=BO﹣AB﹣AE=10﹣6﹣24﹣2,
∴P(4﹣2,2).
如图3中,
根据对称性可知当点P在第四象限时,P(4﹣2,﹣2)时,也满足条件.
综上所述:满足条件的点P坐标(4﹣2,2)或(4﹣2,﹣2),AM的最大值为46.
故答案为:46,(4﹣2,2)或(4﹣2,﹣2).
第二十三章
旋转
23.1
图形的旋转
课后练习
一、单选题
1.如图,菱形OABC的顶点O(0,0),A(﹣2,0),∠B=60°,若菱形绕点O顺时针旋转90°后得到菱形OA1B1C1,依此方式,绕点O连续旋转2020次得到菱形OA2020B2020C2020,那么点C2020的坐标是(
)
A.(,1)
B.(1,﹣)
C.(﹣,﹣1)
D.(﹣1,)
2.如图,△ABC中,∠BAC=90°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1,点C的对应点恰好落在CB的延长线上,连接CB1,则下列说法错误的是( )
A.旋转角为120°
B.ABB1C1
C.S=S
D.AB1=B1C1
3.如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形,图中阴影部分的面积为(
)
A.a2
B.a2
C.(1﹣)a2
D.(1﹣)a2
4.如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为(
)
A.3
B.2.5
C.4
D.2
5.如图,在正方形内作,交于点,交于点,连接,过点作,垂足为点,将绕点顺时针旋转得到,若,则以下结论:①,②,③,④,正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
6.如图,等边三角形的边长为4,点是△的中心,.绕点旋转,分别交线段于两点,连接,给出下列四个结论:①;②;③四边形的面积始终等于;④△周长的最小值为6,上述结论中正确的个数是(
)
A.1
B.2
C.3
D.4
7.如图,在坐标系中放置一菱形
OABC,已知∠ABC=60°,点
B
在
y
轴上,OA=1,先将菱形
OABC
沿
x
轴的正方向无滑动翻转,每次翻转
60°,连续翻转2019次,点
B
的落点依次为
B1,B2,B3,…,则
B2
019
的坐标为(
)
A.(1010,0)
B.(1310.5,
)
C.(1345,
)
D.(1346,0)
8.如图,长方形ABCD的顶点A、B分别在x轴、y轴上,OA=OB=2,AD=4,将长方形ABCD绕点O顺时针旋转,每次旋转90°,则第2021次旋转结束时,点C的坐标为(
)
A.(6,4)
B.(4,6)
C.(-6,4)
D.(-4,6)
9.如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A.
B.
C.
D.1
10.已知正方形ABCD的边长为2,正方形内有一动点P,求点P到三个顶点A、B、C的距离之和的最小值(
)
A.
B.
C.
D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,等腰直角△ABC中,∠ACB=90°,AC=BC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,则点D在运动过程中ME的最小值为_____.
12.四边形、四边形都是正方形,当正方形绕点逆时针旋转45°()时,如图,连接,,并延长交于点,且.若,,则线段的长是________.
13.把一副三角板如图1放置,其中∠ACB=∠DEC=90°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转使CD边恰好过AB的中点O,得到D1C1E1,如图2,则线段AD1的长度为_________.
14.如图,将三个同样的正方形的一个顶点重合放置,那么的度数为__________.
15.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM﹣ON的值不变;(3)△OMN的周长不变;(4)四边形PMON的面积不变,其中正确的序号为_____.
三、解答题
16.如图,四边形ABCD是正方形,点E是BC边上的动点(不与点B、C重合),将射线AE绕点A按逆时针方向旋转45°后交CD边于点F,AE、AF分别交BD于G、H两点.
(1)当∠BEA=55°时,求∠HAD的度数;
(2)设∠BEA=α,试用含α的代数式表示∠DFA的大小;
(3)点E运动的过程中,试探究∠BEA与∠FEA有怎样的数量关系,并说明理由.
17.如图,在梯形ABCD中,ABCD,∠BAD=90°,∠1=∠2=60°.射线AM以每秒2°的速度绕着端点A顺时针旋转至AB处停止,同时射线CN以每秒1°的速度绕端点C顺时针旋转至CD处停止.
(1)射线AM、CN旋转30秒时,∠DAM=
度,∠BCN=
度;
(2)若射线CN先转动80秒,射线AM才开始转动,如图2,当射线AM与射线CN相交所形成的∠AEC=150°时,求射线AM的旋转时间.
(3)如图3,若射线AM、CN同时转动,在射线AM到达AB之前与射线CN交于点E,以点E为顶点作∠AEF交DC的延长线于点F,且∠AEF=130°,请探究此时∠CAE与∠CEF的数量关系,并说明理由.
18.书籍和纸张的长与宽比值都有固定的尺寸,如常用的A3、A4、A5的纸张长与宽的比值都相等.一长方形纸张对折后的小长方形的长与宽的比值与原长方形的长与宽的比值相等.
(1)求满足这样条件的长方形的长与宽的比值;
(2)如图所示的长方形ABCD长与宽之比也满足以上条件,其中宽AB=2.
①点P是AD上一点,将△BPA沿BP折叠得到△BPE,当BE垂直AC时,求AP的长;
②若将长方形ABCD绕点B旋转得到长方形A1BC1D1,直线CC1交DD1于点M,N为BC的中点,直接写出MN的最大值:
.
19.综合与探究
如图,点是等边内一点,将绕点按顺时针方向旋转得到,连接和.
(1)求证:是等边三角形;
(2)若,,,求的长;
(3)若,则_________度时,是等腰三角形?(直接写出答案).
20.的边BC=,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB=
度;
(2)如图,将绕点C顺时针旋转60°,画出旋转后的图形;
(3)AP+BP+CP的最小值为
.
21.如图1,△ABC是等腰直角三角形,AB=BC,∠ABC=90°,线段BD可绕点B在平面内旋转,BD=4.
(1)若AB=8,在线段BD旋转过程中,当点B,C,D三点在同一直线上时,直接写出CD的长.
(2)如图2,若将线段BD绕点B按顺时针方向旋转90°,得到线段BE,连接AE,CE.
①当点D的位置由△ABC外的点D转到其内的点E处,且∠AEB=135°,AE=2时,求CE的长;
②如图3,若AB=8,连接DE,将△BDE绕点B在平面内旋转,分别取DE,AE,AC的中点M,P,N,连接MP,PN,NM,请直接写出△MPN面积S的取值范围.
22.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
23.(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取到最大值,且最大值为 ;(用含a、b的式子表示).
(2)如图2,若点A为线段BC外一动点,且BC=6,AB=3,分别以AB,AC为边,作等边△ABD和等边△ACE,连接CD,BE.
①图中与线段BE相等的线段是线段 ,并说明理由;
②直接写出线段BE长的最大值为 .
(3)如图3,在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(10,0),点P为线段AB外一动点,且PA=4,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值为 ,及此时点P的坐标为 .
(提示:等腰直角三角形的三边长a、b、c满足a:b:c=1:1:)
【参考答案】
1.D
2.D
3.D
4.C
5.C
6.C
7.D
8.A
9.A
10.C
11.2.
12.
13.5
14.20°.
15.(1)(4)
16.解:(1)∵四边形ABCD是正方形,
∴∠EBA=∠BAD=90°,
∴∠EAB=90°﹣∠BAE=90°﹣55°=35°,
∴∠HAD=∠BAD﹣∠EAF﹣∠EAB=90°﹣45°﹣35°=10°;
(2)∵四边形ABCD是正方形,
∴∠EBA=∠BAD=∠ADF=90°,
∴∠EAB=90°﹣∠BAE=90°﹣α,
∴∠DAF=∠BAD﹣∠EAF﹣∠EAB=,
∴∠DFA=90°﹣∠DAF==135°﹣α;
(3)∠BEA=∠FEA,理由如下:
延长CB至I,使BI=DF,连接AI.
∵四边形ABCD是正方形,
∴AD=AB,∠ADF=∠ABC=90°,
∴∠ABI=90°,
又∵BI=DF,
∴△DAF≌△BAI(SAS),
∴AF=AI,∠DAF=∠BAI,
∴∠EAI=∠BAI+∠BAE=∠DAF+∠BAE=45°=∠EAF,
又∵AE是△EAI与△EAF的公共边,
∴△EAI≌△EAF(SAS),
∴∠BEA=∠FEA.
17.解:(1)∵射线AM以每秒2°的速度绕着端点A顺时针旋转,射线CN以每秒1°的速度绕端点C顺时针旋转,
∴射线AM、CN旋转30秒时,∠DAM=30×2°=60°,∠BCN=30×1°=30°,
故答案为60,30;
(2)根据题意画出图形如图2:
∵在梯形ABCD中,AB∥CD,∠BAD=90°,∠1=∠2=60°.
∴∠CAB=30°,
∴∠ACB=90°,
设射线AM的旋转时间为x秒,则射线CN旋转的时间为(80+x)秒,
∴∠MAM′=2x,∠NCN′=80+x,
∴∠CAM′=∠1﹣∠MAM′=60﹣2x,ACN′=80+x﹣90=x﹣10,
∵∠AEC=150°,
∴60﹣2x+x﹣10+150=180,
解得x=20,
即射线AM的旋转时间为20秒;
(3)∠CAE=2∠CEF﹣20°,
理由:设射线转动时间为t秒,如图3,
∵∠DAE=2t,
∴∠CAE=2t﹣60°,
又∵∠BCE=t,
∴∠ACE=90°﹣t,
∴∠AEC=180°﹣∠CAE﹣∠ACE=150°﹣t,而∠AEF=130°,
∴∠CEF=130°﹣∠AEC=130°﹣(150°﹣t)=t﹣20°,
∴∠CAE=2∠CEF﹣20°.
18.(1)设长方形的长与宽分别为a,b.
由题意:,
∴a2=2b2,
∴;
(2)①如图1中,延长PE、BC交于点G,
∵∠PEB=90°,
∴PE⊥BE,
∵BE⊥AC,BE⊥PE,
∴PG∥AC,
∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=2,AD∥BG,∠ABC=90°,
∴四边形APGC是平行四边形,
∴PG=AC===2,
∵AD∥BC,
∴∠APB=∠GBP,
∵∠APB=∠GPB,
∴∠GBP=∠GPB,
∴GP=GB=2,
∴AP=CG=BG=BC=2﹣2;
②如图2中,连接BM,取BD的中点O,连接OM,ON,延长CC1到K,使得C1K=CC1在MK的延长线上取一点J,使得D1J=D1K,连接BD1.
∵BC=BC1,
∴∠BCC1=∠BC1C,
∵∠BC1D1=∠BCD=90°,
∴∠D1C1K+∠BC1C=90°,∠BCC1+∠DCC1=90°,
∴∠D1C2K=∠DCC1,
∵CD=C1D1,CC1=C1K,
∴△DCC1≌△D1C1K(SAS),
∴DC1=KD1=JD1,∠CC1D=∠C1KD1,
∵∠JKD1+∠C1JKD1=180°,∠CC1D+∠DC1M=180°,
∴∠DC1M=∠D1KJ,
∵D1J=D1K,
∴∠J=∠D1KJ,
∴∠J=∠DC1M,
∵∠D1MJ=∠DMC1,
∴△D1MJ≌△DMC1(AAS),
∴D1M=DM′,
∵BD=BD1,
∴BM⊥DD1,
取BD的中点O,连接OM,ON,
∵∠BMD=90°,
∴OM=BD=,
∵BO=OD,BN=CN,
∴ON=CD=1,
∵MN≤OM+ON,
∴MN≤+1,
∴MN的最大值为+1.
故答案为:+1.
19.(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)解:由(1)知△COD是等边三角形;
∴
OD=OC=4,∠ODC=60°,
∵
将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴AD=OB=3,∠ADC=∠BOC=150°,
∴∠ADO=∠ADC-∠ODC=90°,
∴OA=;
(3)解:设∠BOC=α,
①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠OAD=180°-(∠AOD+∠ADO)=180°-(190°-α+α-60°)=50°,
∴α-60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵∠AOD=360°-110°-60°-α=190°-α,
∠OAD==120°-
∴190°-α=120°-,
解得α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
故答案为:125或110或140.
20.(1)∵点A在BC的垂直平分线上,
∴AB=AC,
∴∠ACB=∠ABC=30°,
故答案为:30;
(2)如图:
(3)如图,连接、AB、A,
由旋转得AP=A,PC=C,AC=C,∠AC=∠PC=60°,
∴△PC、△AC都是等边三角形,
∴PC=P,∠AC=60°,
∵∠ACB=∠ABC=30°,
∴∠AC=∠ACB+∠ABC,即B、A、三点共线,
∵∠CB=∠CA+∠ACB=90°,∠BC=60°,BC=,
∴B=,
当B、P、、四点共线时,AP+BP+CP=PB++A值的最小,
∴AP+BP+CP=B=4,
故答案为:4.
21.解:(1)当点D在CB的延长线上时,CD=4+8=12,
当点D在线段BC上时,CD=8﹣4=4,
故CD的长为4或12.
(2)①如图2中,连接AD,DE.
∵BD=BE=4,∠DBE=90°,
∴,∠DEB=45°,
∵∠AEB=135°,
∴∠AED=90°,
∵,
∴
∵∠DBE=∠ABC=90°,
∴∠DBA=∠EBC,
∵BD=BE,BA=BC,
∴△DBA≌△EBC(SAS),
∴.
②如图3中,连接AD,延长CE交AB于O,交AD于J.
∵∠DBE=∠ABC=90°,
∴∠DBA=∠EBC,
∵BD=BE,BA=BC,
∴△DBA≌△EBC(SAS),
∴EC=AD,∠DAB=∠ECB,
∵∠BOC+∠BCE=90°,∠AOJ=∠BOC,
∴∠AOJ+∠DAB=90°,
∴∠AJC=90°,
∴CJ⊥AD,
∵AP=EP,EM=MD,
∴PM∥AD,,
同法可得,PN∥EC,,
∴PM=PN,PM⊥JC,
∴PN⊥PM,
∴△PMN是等腰直角三角形,
∴
∵4≤AD≤12,
∴2≤S△PMN≤18.
22.证明:(1)∵将线段AD绕点A逆时针旋转60°得到线段AE
∴AD=AE,∠DAE=60°
∴△ADE是等边三角形
∵△ABC为等边三角形
∴AB=AC,
∠BAC=∠DAE=60°
∴∠DAB=∠CAE,且AB=AC,AD=AE
∴△ADB≌△AEC(SAS)
∴BD=CE
(2)如图,过点C作CG∥BP,交EF的延长线于点G
∵∠ADB=90°,
∠ADE=60°
∴∠BDG=30°
∵CG∥BP
∴∠G=∠BDG=30°
∵△ADB≌△AEC
∴BD=CE,∠ADB=∠AEC=90°
∴∠GEC=∠AEC﹣∠AED=30°
∴∠G=∠GEC=30°
∴GC=CE
∴CG=BD,且∠BDG=∠G,
∠BFD=∠GFC
∴△BFD≌△CFG(AAS)
∴BF=FC
∴点F是BC中点
(3)如图,连接AF,
∵△ABC是等边三角形,BF=FC
∴AF⊥BC
∴∠AFC=90°
∴∠AFC=∠AEC=90°
∴点A,点F,点C,点E四点在以AC为直径的圆上
∴EF最大为直径,
即最大值为1
23.(1)∵点A为线段BC外一动点,且BC=a,AB=b,
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.
故答案为:CB的延长线上,a+b;
(2)①CD=BE,
理由:∵△ABD与△ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB.
在△CAD与△EAB中,
,
∴△CAD≌△EAB(SAS),
∴CD=BE.
故答案是:CD;
②∵线段BE长的最大值=线段CD的最大值,
由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,
∴最大值为BD+BC=AB+BC=9.
故答案为:CD=BE=9.
(3)如图1,
∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,
则△APN是等腰直角三角形,
∴PN=PA=2,BN=AM.
∵A的坐标为(4,0),点B的坐标为(10,0),
∴OA=4,OB=10,∴AB=6,
∴线段AM长的最大值=线段BN长的最大值,
∴当N在线段BA的延长线时,线段BN取得最大值,
最大值=AB+AN.
∵ANAP=4,
∴最大值为46.
如图2,
过P作PE⊥x轴于E.
∵△APN是等腰直角三角形,
∴PE=AE=2,
∴OE=BO﹣AB﹣AE=10﹣6﹣24﹣2,
∴P(4﹣2,2).
如图3中,
根据对称性可知当点P在第四象限时,P(4﹣2,﹣2)时,也满足条件.
综上所述:满足条件的点P坐标(4﹣2,2)或(4﹣2,﹣2),AM的最大值为46.
故答案为:46,(4﹣2,2)或(4﹣2,﹣2).
同课章节目录
