人教版九年级上册数学24.1.4圆心角和圆周角教案
文档属性
| 名称 | 人教版九年级上册数学24.1.4圆心角和圆周角教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 640.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 00:00:00 | ||
图片预览

文档简介
圆心角和圆周角及之间的关系
内容(课题):圆心角和圆周角及之间的关系
教学目的:1、了解圆周角的概念。2、理解圆周角定理的证明。3、通过圆周角定理的证明,培养学生对数学的逻辑严密性的体验,树立正确的数学学习观。4、培养学生的合作交流意识和数学交流能力。
重难点(
考点)分析:
要注意分类讨论和有关圆的问题的多解性,同时结合阅读理解,条件开放,结论开放的探索题型,圆周角的概念和圆周角定理的证明,理解圆周角定理的证明中的分类证明思想。
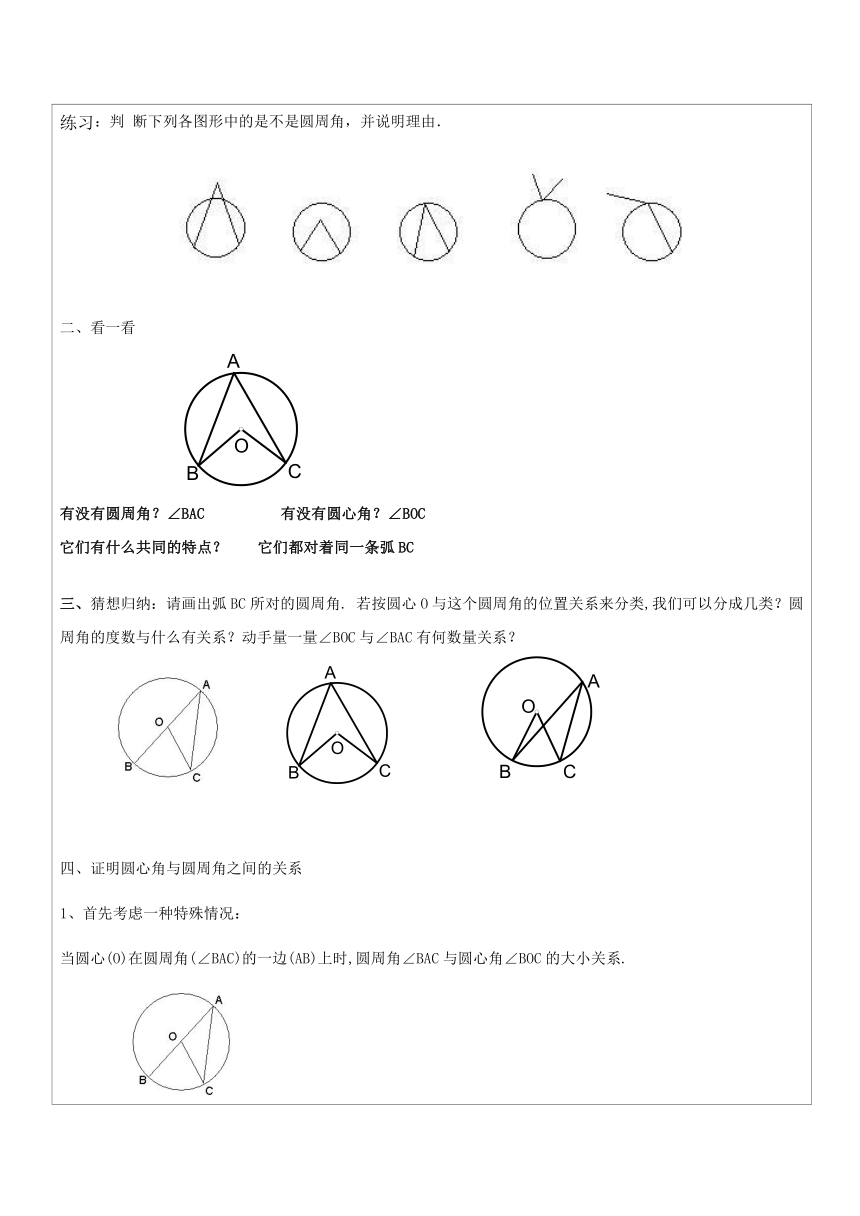
教学过程:一、圆周角与圆心角的定义顶点在圆上,并且两边都和圆相交的角叫做圆周角。注意圆周角定义的两个基本特征:顶点在圆上;(2)两边都和圆相交。
圆心角:顶点在圆心的角。利用两个错误的图形来强调圆周角定义的两个基本特征:练习:判
断下列各图形中的是不是圆周角,并说明理由.二、看一看
有没有圆周角?∠BAC
有没有圆心角?∠BOC它们有什么共同的特点?
它们都对着同一条弧BC三、猜想归纳:请画出弧BC所对的圆周角.
若按圆心O与这个圆周角的位置关系来分类,我们可以分成几类?圆周角的度数与什么有关系?动手量一量∠BOC与∠BAC有何数量关系?
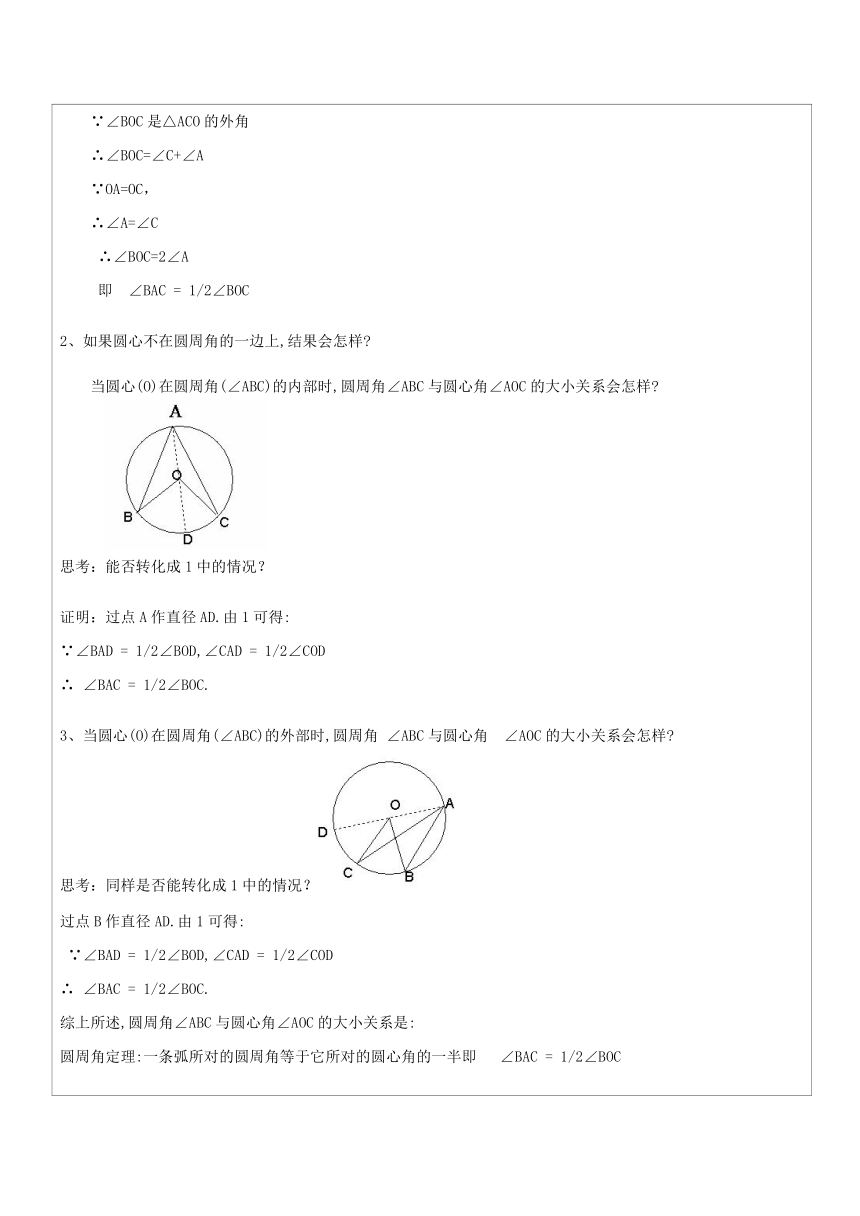
证明圆心角与圆周角之间的关系首先考虑一种特殊情况:当圆心(O)在圆周角(∠BAC)的一边(AB)上时,圆周角∠BAC与圆心角∠BOC的大小关系.
∵∠BOC是△ACO的外角
∴∠BOC=∠C+∠A
∵OA=OC,
∴∠A=∠C
∴∠BOC=2∠A
即
∠BAC
=
1/2∠BOC如果圆心不在圆周角的一边上,结果会怎样?
当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
思考:能否转化成1中的情况?证明:过点A作直径AD.由1可得:
∵∠BAD
=
1/2∠BOD,∠CAD
=
1/2∠COD∴
∠BAC
=
1/2∠BOC.
3、当圆心(O)在圆周角(∠ABC)的外部时,圆周角
∠ABC与圆心角
∠AOC的大小关系会怎样?
思考:同样是否能转化成1中的情况?过点B作直径AD.由1可得:
∵∠BAD
=
1/2∠BOD,∠CAD
=
1/2∠COD∴
∠BAC
=
1/2∠BOC.综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半即
∠BAC
=
1/2∠BOC知识点总结:圆周角与圆心角的关系
(1).在同圆或等圆中,如果两条弦,两条弧,两个圆心角中有一组量相等,那么它们所对应的其它各组量都分别相等。(2).一条弧所对的圆周角等于这条弧所对的圆心角的一半。(3).直径所对的圆周角是90度,90度的圆周角所对的弦是直径。(4).圆的内接四边形对角之和是180度。(5).弧的度数就是圆心角的度数。练习题:(一)选择、填空题:1.在⊙O中,同弦所对的圆周角(
)A.相等
B.互补
C.相等或互补
D.都不对3.下列说法正确的是(
)A.顶点在圆上的角是圆周角B.两边都和圆相交的角是圆周角C.圆心角是圆周角的2倍D.圆周角度数等于它所对圆心角度数的一半4.下列说法错误的是(
)A.等弧所对圆周角相等
B.同弧所对圆周角相等C.同圆中,相等的圆周角所对弧也相等.
D.同圆中,等弦所对的圆周角相等5.如图4,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角.若∠BCD=25°,则∠AOD=
.6.如图5,⊙O直径MN⊥AB于P,∠BMN=30°,则∠AON=
.7.⊙O的弦AB等于半径,那么弦AB所对的圆周角一定是(
).
(A)30° (B)150° (C)30°或150° (D))60°
8.△ABC中,∠B=90°,以BC为直径作圆交AC于E,若BC=12,AB=12
,则
的度数为(
)
(A)60° (B)80° (C)100° (D))120°
9.如图,△ABC是⊙O的内接等边三角形,D是AB上一点,AB与CD交于E点,则图中60°的角共有(
)个.
(A)3 (B)4 (C)5 (D)610.如图,△ABC内接于⊙O,∠OBC=25°,则∠A的度数为(
)
(A)70°
(B)65°
(C)60°
(D))50°填空题:1.如图4,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.
(1)
(2)
(3)如图5,AB是⊙O的直径,
,∠A=25°,则∠BOD的度数为________.3.如图6,AB是半圆O的直径,AC=AD,OC=2,∠CAB=
30
°,
则点O
到CD
的距离OE=______.三、解答题:1.如图,已知是的直径,是弦,过点作于,连结.(1)求证:;(2)若,求的度数.2.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.
3.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC=
∠CAD,求弦AC的长.
能力提升:如图1,AB是半⊙O的直径,过A、B两点作半⊙O的弦,当两弦交点恰好落在半⊙O上C点时,则有AC·AC+BC·BC=AB2.(1)如图2,若两弦交于点P在半⊙O内,则AP·AC+BP·BD=AB2是否成立?请说明理由.(2)如图3,若两弦AC、BD的延长线交于P点,则AB2=
.参照(1)填写相应结论,并证明你填写结论的正确性.
学生对于本次课的评价:○
特别满意
○
满意
○
一般
○
差
学生签字:________
教学总结:
(图1)
内容(课题):圆心角和圆周角及之间的关系
教学目的:1、了解圆周角的概念。2、理解圆周角定理的证明。3、通过圆周角定理的证明,培养学生对数学的逻辑严密性的体验,树立正确的数学学习观。4、培养学生的合作交流意识和数学交流能力。
重难点(
考点)分析:
要注意分类讨论和有关圆的问题的多解性,同时结合阅读理解,条件开放,结论开放的探索题型,圆周角的概念和圆周角定理的证明,理解圆周角定理的证明中的分类证明思想。
教学过程:一、圆周角与圆心角的定义顶点在圆上,并且两边都和圆相交的角叫做圆周角。注意圆周角定义的两个基本特征:顶点在圆上;(2)两边都和圆相交。
圆心角:顶点在圆心的角。利用两个错误的图形来强调圆周角定义的两个基本特征:练习:判
断下列各图形中的是不是圆周角,并说明理由.二、看一看
有没有圆周角?∠BAC
有没有圆心角?∠BOC它们有什么共同的特点?
它们都对着同一条弧BC三、猜想归纳:请画出弧BC所对的圆周角.
若按圆心O与这个圆周角的位置关系来分类,我们可以分成几类?圆周角的度数与什么有关系?动手量一量∠BOC与∠BAC有何数量关系?
证明圆心角与圆周角之间的关系首先考虑一种特殊情况:当圆心(O)在圆周角(∠BAC)的一边(AB)上时,圆周角∠BAC与圆心角∠BOC的大小关系.
∵∠BOC是△ACO的外角
∴∠BOC=∠C+∠A
∵OA=OC,
∴∠A=∠C
∴∠BOC=2∠A
即
∠BAC
=
1/2∠BOC如果圆心不在圆周角的一边上,结果会怎样?
当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
思考:能否转化成1中的情况?证明:过点A作直径AD.由1可得:
∵∠BAD
=
1/2∠BOD,∠CAD
=
1/2∠COD∴
∠BAC
=
1/2∠BOC.
3、当圆心(O)在圆周角(∠ABC)的外部时,圆周角
∠ABC与圆心角
∠AOC的大小关系会怎样?
思考:同样是否能转化成1中的情况?过点B作直径AD.由1可得:
∵∠BAD
=
1/2∠BOD,∠CAD
=
1/2∠COD∴
∠BAC
=
1/2∠BOC.综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半即
∠BAC
=
1/2∠BOC知识点总结:圆周角与圆心角的关系
(1).在同圆或等圆中,如果两条弦,两条弧,两个圆心角中有一组量相等,那么它们所对应的其它各组量都分别相等。(2).一条弧所对的圆周角等于这条弧所对的圆心角的一半。(3).直径所对的圆周角是90度,90度的圆周角所对的弦是直径。(4).圆的内接四边形对角之和是180度。(5).弧的度数就是圆心角的度数。练习题:(一)选择、填空题:1.在⊙O中,同弦所对的圆周角(
)A.相等
B.互补
C.相等或互补
D.都不对3.下列说法正确的是(
)A.顶点在圆上的角是圆周角B.两边都和圆相交的角是圆周角C.圆心角是圆周角的2倍D.圆周角度数等于它所对圆心角度数的一半4.下列说法错误的是(
)A.等弧所对圆周角相等
B.同弧所对圆周角相等C.同圆中,相等的圆周角所对弧也相等.
D.同圆中,等弦所对的圆周角相等5.如图4,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角.若∠BCD=25°,则∠AOD=
.6.如图5,⊙O直径MN⊥AB于P,∠BMN=30°,则∠AON=
.7.⊙O的弦AB等于半径,那么弦AB所对的圆周角一定是(
).
(A)30° (B)150° (C)30°或150° (D))60°
8.△ABC中,∠B=90°,以BC为直径作圆交AC于E,若BC=12,AB=12
,则
的度数为(
)
(A)60° (B)80° (C)100° (D))120°
9.如图,△ABC是⊙O的内接等边三角形,D是AB上一点,AB与CD交于E点,则图中60°的角共有(
)个.
(A)3 (B)4 (C)5 (D)610.如图,△ABC内接于⊙O,∠OBC=25°,则∠A的度数为(
)
(A)70°
(B)65°
(C)60°
(D))50°填空题:1.如图4,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.
(1)
(2)
(3)如图5,AB是⊙O的直径,
,∠A=25°,则∠BOD的度数为________.3.如图6,AB是半圆O的直径,AC=AD,OC=2,∠CAB=
30
°,
则点O
到CD
的距离OE=______.三、解答题:1.如图,已知是的直径,是弦,过点作于,连结.(1)求证:;(2)若,求的度数.2.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.
3.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC=
∠CAD,求弦AC的长.
能力提升:如图1,AB是半⊙O的直径,过A、B两点作半⊙O的弦,当两弦交点恰好落在半⊙O上C点时,则有AC·AC+BC·BC=AB2.(1)如图2,若两弦交于点P在半⊙O内,则AP·AC+BP·BD=AB2是否成立?请说明理由.(2)如图3,若两弦AC、BD的延长线交于P点,则AB2=
.参照(1)填写相应结论,并证明你填写结论的正确性.
学生对于本次课的评价:○
特别满意
○
满意
○
一般
○
差
学生签字:________
教学总结:
(图1)
同课章节目录
