北师大版数学 九年级上册 1.3.正方形性质与判定课件(17张)
文档属性
| 名称 | 北师大版数学 九年级上册 1.3.正方形性质与判定课件(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 970.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 00:08:50 | ||
图片预览





文档简介
一、创设情境 导入新课
问题1:平行四边形具有哪些性质?
问题2:菱形、矩形是特殊的平行四边形,
它们具有哪些性质?
边
角
对角线
对称性
平行四
边形
菱形
矩形
边
角
对角线
对称性
一、创设情境 导入新课
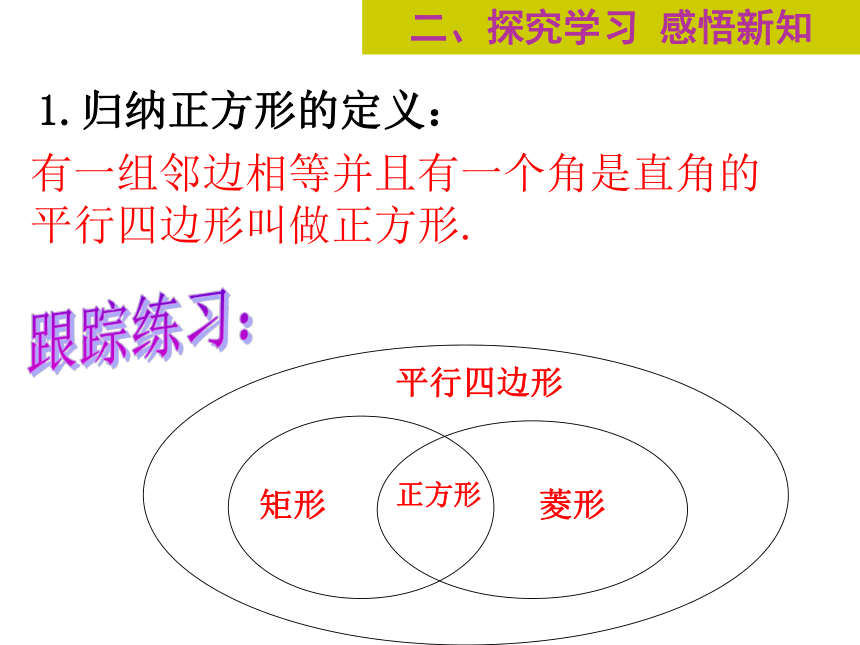
二、探究学习 感悟新知
1.归纳正方形的定义:
有一组邻边相等并且有一个角是直角的
平行四边形叫做正方形.
平行四边形
矩形
菱形
正方形
2.探究正方形的性质:
二、探究学习 感悟新知
(1)想一想:
①正方形是特殊的平行四边形,它具有一般平行
四边形的所有性质.你能举一些这样的性质吗?
②正方形是轴对称图形吗?
如果是,它有几条对称轴?
③你认为正方形还具有哪些特殊的性质?
与同伴交流.
结论:正方形是轴对称图形.
二、探究学习 感悟新知
(2)问题:正方形的边具有怎样的性质?
(3)问题:正方形的角除了“有一个内角是直角”外,
还具有哪些一般平行四边形不具备的性质?
(4)问题:正方形的边除了“有一组邻边相等”外,
还具有哪些一般平行四边形不具备的性质?
(5)问题:正方形的对角线有什么性质?
结论:对边平行且相等.
结论:正方形的四个角都是直角.
结论:正方形的四条边相等
结论:正方形的对角线相等且互相垂直平分.
二、探究学习 感悟新知
3.证明正方形的性质:
已知:如图所示,四边形ABCD是正方形,
∠ABC=90°,AB=BC,对角线AC与BD交于点O.
求证:(1)∠ABC =∠BCD =∠CDA =∠DAB =90°
(2)AB =BC =CD =DA
(3) AC =BD,AC⊥BD且AC与BD互相平分
二、探究学习 感悟新知
证明:(1)∵四边形ABCD是正方形
∴∠ABC =∠CDA,∠BCD =∠DA,AB∥DC
∴∠ABC +∠BCD =180°
又∵∠ABC =90°
∴∠BCD =90°
∴∠ABC =∠BCD =∠CDA =∠DAB =90°
(2)∵四边形ABCD是正方形
∴AB =CD AD =BC
又∵AB =BC
∴AB =BC =CD =DA
二、探究学习 感悟新知
(3)∵四边形ABCD是正方形
∴OA =OC,OB =OD
∵AB =BC
∴△ABC为等腰三角形
∴BO⊥AC,∴AC⊥BD
在△ABC和△DCB中,
∵AB=DC,∠ABC =∠BCD,BC=CB
∴△ABC≌△DCB
∴AC=DB
①正方形具有而菱形没有的性质是( )
A.对角线互相平分 B.每条对角线平分一组对角
C.对角线相等 D.对边相等
②正方形具有而矩形不一定具有的特征是( )
A.四个角都是直角 B.对角线相等
C.四条边相等 D.对角线互相平分
③平行四边形、矩形、菱形、正方形都具有的性质
是( )
A.对角线相等 B.对角线互相平分
C.对角线平分一组对角 D.对角线互相垂直
④若正方形的面积为4 ,则它的边长为( ),
对角线长为 ( ) .
二、探究学习 感悟新知
C
C
B
2cm
4.归纳正方形的性质:
(1)正方形的对边平行且相等且四条边相等;
(2)正方形的四个角都是直角;
(3)正方形的对角线相等且互相垂直平分;
(4)正方形是轴对称图形,有4条对称轴.
二、探究学习 感悟新知
三、例题解析 应用新知
例1:如图所示,在正方形ABCD中,E为CD边上一点,
F为BC延长线上一点,且CE=CF.
BE与DF之间有怎样的关系?请说明理由.
A
B
C
D
E
F
解:BE =DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD正方形
∴BC =DC,∠BCE =90°
∴∠DCF =180°-∠BCE
=180°-90°
=90°
∴∠BCE =∠DCF
又∵CE =CF
∴△BCE ≌△DCF
∴BE =DF
三、例题解析 应用新知
(2)延长BE交DF于点M
∵△BCE ≌△DCF
∴∠CBE =∠CDF
∵∠DCF =90°
∴∠CDF +∠F =90°
∴∠CBE +∠F =90°
∴∠BMF =90°
∴BE⊥DF
A
B
C
D
F
E
M
E
四、回顾反思 提炼升华
正方形
名称
特征
性 质
定 义
边
角
对角线
轴对称性
有一组邻边相等且有一个内角是直角的平行四边形叫做正方形
对边平行且相等,四条边相等
对角线相等且互相垂直平分
轴对称图形,有4条对称轴
四个角都是直角
五、达标检测 反馈提高
判断题
(1)对角线互相垂直且相等的四边形是正方形.( )
(2)如果一个菱形的对角线相等,那么它一定是正方形.( )
(3)如果一个矩形的对角线互相垂直,那么它一定是正方形.( )
2. 如图,正方形ABCD的周长为15cm , 则矩形EFCG的周长是__________.
3. 如图,点E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE的度数为______.
祝愿同学们:
象雄鹰一样
飞的更高,
飞的更远!
问题1:平行四边形具有哪些性质?
问题2:菱形、矩形是特殊的平行四边形,
它们具有哪些性质?
边
角
对角线
对称性
平行四
边形
菱形
矩形
边
角
对角线
对称性
一、创设情境 导入新课
二、探究学习 感悟新知
1.归纳正方形的定义:
有一组邻边相等并且有一个角是直角的
平行四边形叫做正方形.
平行四边形
矩形
菱形
正方形
2.探究正方形的性质:
二、探究学习 感悟新知
(1)想一想:
①正方形是特殊的平行四边形,它具有一般平行
四边形的所有性质.你能举一些这样的性质吗?
②正方形是轴对称图形吗?
如果是,它有几条对称轴?
③你认为正方形还具有哪些特殊的性质?
与同伴交流.
结论:正方形是轴对称图形.
二、探究学习 感悟新知
(2)问题:正方形的边具有怎样的性质?
(3)问题:正方形的角除了“有一个内角是直角”外,
还具有哪些一般平行四边形不具备的性质?
(4)问题:正方形的边除了“有一组邻边相等”外,
还具有哪些一般平行四边形不具备的性质?
(5)问题:正方形的对角线有什么性质?
结论:对边平行且相等.
结论:正方形的四个角都是直角.
结论:正方形的四条边相等
结论:正方形的对角线相等且互相垂直平分.
二、探究学习 感悟新知
3.证明正方形的性质:
已知:如图所示,四边形ABCD是正方形,
∠ABC=90°,AB=BC,对角线AC与BD交于点O.
求证:(1)∠ABC =∠BCD =∠CDA =∠DAB =90°
(2)AB =BC =CD =DA
(3) AC =BD,AC⊥BD且AC与BD互相平分
二、探究学习 感悟新知
证明:(1)∵四边形ABCD是正方形
∴∠ABC =∠CDA,∠BCD =∠DA,AB∥DC
∴∠ABC +∠BCD =180°
又∵∠ABC =90°
∴∠BCD =90°
∴∠ABC =∠BCD =∠CDA =∠DAB =90°
(2)∵四边形ABCD是正方形
∴AB =CD AD =BC
又∵AB =BC
∴AB =BC =CD =DA
二、探究学习 感悟新知
(3)∵四边形ABCD是正方形
∴OA =OC,OB =OD
∵AB =BC
∴△ABC为等腰三角形
∴BO⊥AC,∴AC⊥BD
在△ABC和△DCB中,
∵AB=DC,∠ABC =∠BCD,BC=CB
∴△ABC≌△DCB
∴AC=DB
①正方形具有而菱形没有的性质是( )
A.对角线互相平分 B.每条对角线平分一组对角
C.对角线相等 D.对边相等
②正方形具有而矩形不一定具有的特征是( )
A.四个角都是直角 B.对角线相等
C.四条边相等 D.对角线互相平分
③平行四边形、矩形、菱形、正方形都具有的性质
是( )
A.对角线相等 B.对角线互相平分
C.对角线平分一组对角 D.对角线互相垂直
④若正方形的面积为4 ,则它的边长为( ),
对角线长为 ( ) .
二、探究学习 感悟新知
C
C
B
2cm
4.归纳正方形的性质:
(1)正方形的对边平行且相等且四条边相等;
(2)正方形的四个角都是直角;
(3)正方形的对角线相等且互相垂直平分;
(4)正方形是轴对称图形,有4条对称轴.
二、探究学习 感悟新知
三、例题解析 应用新知
例1:如图所示,在正方形ABCD中,E为CD边上一点,
F为BC延长线上一点,且CE=CF.
BE与DF之间有怎样的关系?请说明理由.
A
B
C
D
E
F
解:BE =DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD正方形
∴BC =DC,∠BCE =90°
∴∠DCF =180°-∠BCE
=180°-90°
=90°
∴∠BCE =∠DCF
又∵CE =CF
∴△BCE ≌△DCF
∴BE =DF
三、例题解析 应用新知
(2)延长BE交DF于点M
∵△BCE ≌△DCF
∴∠CBE =∠CDF
∵∠DCF =90°
∴∠CDF +∠F =90°
∴∠CBE +∠F =90°
∴∠BMF =90°
∴BE⊥DF
A
B
C
D
F
E
M
E
四、回顾反思 提炼升华
正方形
名称
特征
性 质
定 义
边
角
对角线
轴对称性
有一组邻边相等且有一个内角是直角的平行四边形叫做正方形
对边平行且相等,四条边相等
对角线相等且互相垂直平分
轴对称图形,有4条对称轴
四个角都是直角
五、达标检测 反馈提高
判断题
(1)对角线互相垂直且相等的四边形是正方形.( )
(2)如果一个菱形的对角线相等,那么它一定是正方形.( )
(3)如果一个矩形的对角线互相垂直,那么它一定是正方形.( )
2. 如图,正方形ABCD的周长为15cm , 则矩形EFCG的周长是__________.
3. 如图,点E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE的度数为______.
祝愿同学们:
象雄鹰一样
飞的更高,
飞的更远!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
